Distanza di un punto da una retta nel piano

 - 

Coordinate cartesiane e retta nel piano

La distanza di un punto P = (x₀, y₀) da una retta del piano r di equazione implicita ax+by+c=0 è data da d = |ax₀+by₀+c| / √(a^2+b^2) (formula della distanza punto-retta). Si tratta in particolare della distanza più piccola tra tutte le possibili distanze prese tra un qualunque punto appartenente alla retta r e il punto P dato.

Dopo aver visto nelle scorse lezioni le definizioni di distanza tra due punti nel piano e di rette perpendicolari, in questa lezione vedremo il concetto di distanza di un punto da una retta del piano. In particolare, presenteremo due formule per il calcolo della distanza tra un punto ed una retta nel piano cartesiano, nelle quali l’equazione della retta è data rispettivamente in forma implicita ed esplicita.

Nella prima parte della lezione ci limiteremo a fornire la formula della distanza punto-retta nel caso dell’equazione della retta data in forma implicita, fornendo degli esempi. Successivamente, invece, vedremo come ricavare la formula e ne presenteremo anche la variante relativa all’equazione della retta data in forma esplicita.

Nel ricavare la formula per il calcolo della distanza tra un punto ed una retta del piano utilizzeremo i concetti di perpendicolarità tra rette e la formula per il calcolo della distanza tra due punti del piano cartesiano. Nonostante sia sicuramente utile avere presenti tali concetti, nel corso della lezione forniremo comunque i richiami teorici necessari in merito.

Formula per il calcolo della distanza di un punto da una retta del piano

Sia dato un punto {P=(x_0, y_0)} del piano cartesiano. Sia inoltre data una retta {r} del piano cartesiano, con equazione in forma implicita {ax+by+c=0}, con {a,b,c \in \mathbb{R}} e {a, b} mai contemporaneamente nulli.

La distanza tra un punto {P=(x_0, y_0)} ed una retta {r:ax+by+c=0} del piano cartesiano è data da:{d=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}}ovvero può essere calcolata in funzione delle quantità {a,b,c} che compaiono nell’equazione della retta in forma implicita e delle coordinate cartesiane del punto {P}.

Tale distanza {d} (che si può anche indicare in modo più preciso come {d(P, r)}) è presa lungo la perpendicolare alla retta {r} tale da passare per il punto {P}. In altre parole, la distanza è misurata lungo la retta perpendicolare a {r} che congiunge il punto {P} alla retta {r} stessa (la retta {r'} nella figura a seguire).

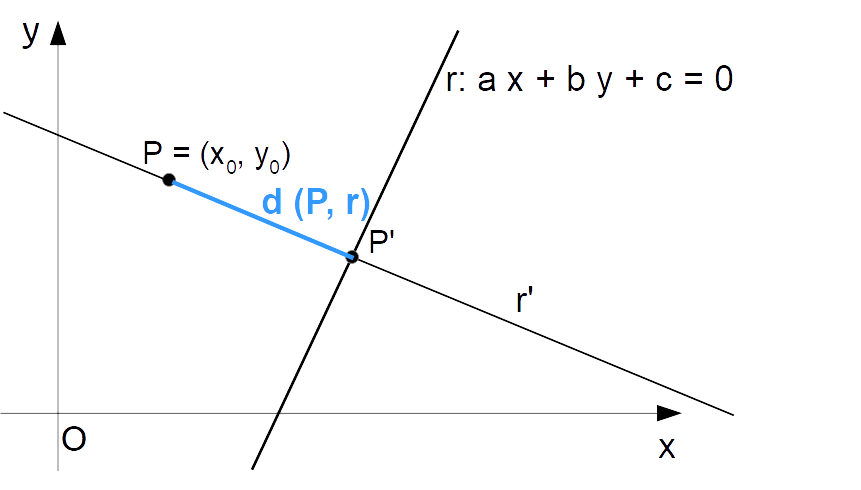
Il punto {P'} rappresenta il punto di intersezione tra le rette {r} ed {r'}. E la distanza tra il punto {P} e la retta {r} effettivamente corrisponde alla distanza tra i due punti {P} e {P'}, ovvero {|PP'|}.

Esempi sul calcolo della distanza di un punto da una retta

Esempio 1

Calcolare la distanza nel piano cartesiano tra il punto {P=(2,5)} e la retta {r} di equazione {4x-2y+3=0}.

Nel caso in esame abbiamo {x_0=2, y_0=5} ed inoltre {a=4, b=-2} ed infine {c=3}. Sostituendo nella formula abbiamo:

\begin{align*} &d = \dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}=\dfrac{|4 \cdot 2+(-2)\cdot5+3|}{\sqrt{4^2+(-2)^2}}=\\ \\ & =\dfrac{|8-10+3|}{\sqrt{16+4}}=\dfrac{|1|}{\sqrt{20}}=\dfrac{1}{\sqrt{5\cdot2^2}}=\dfrac{1}{2\sqrt{5}} \end{align*}

Esempio 2

Con questo esempio vogliamo anticipare come comportarsi nel caso in cui l’equazione della retta sia data nella forma esplicita. Nei paragrafi a seguire forniremo comunque tutti i dettagli in merito.

Calcolare la distanza del punto {P=(-3,7)} dalla retta {r} di equazione {y=2x-8}.

Osserviamo che in questo caso l’equazione della retta {r} è data in forma esplicita. Di conseguenza, per poter applicare la formula per il calcolo della distanza tra il punto e la retta nella forma sin qui nota, dovremo prima di tutto ricondurre l’equazione della retta {r} alla forma implicita. Per quanto visto in precedenza sul passaggio dalla forma esplicita alla forma implicita dell’equazione di una retta, si ha, trasportando opportunamente i termini:

y=2x-8 \quad \Rightarrow \quad 2x-y-8=0

Così l’equazione della retta data in forma implicita è {2x-y-8}, con {a=2, b=-1, c=-8}. Essendo quindi note le quantità {a,b,c} e le coordinate del punto {P}, possiamo procedere con il calcolo della distanza tra il punto {P} e la retta {r}:

\small d=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}=\dfrac{|2 \cdot (-3)+(-1)\cdot7-8|}{\sqrt{2^2+(-1)^2}}=\dfrac{|-6-7-8|}{\sqrt{4+1}}=\dfrac{21}{\sqrt{5}}

Attenzione. Nella formula della distanza di un punto da una retta, non dimentichiamo mai il simbolo di modulo al numeratore.

Calcolo della distanza di un punto da una retta con equazione data in forma esplicita

Supponiamo di dover calcolare la distanza di un punto {P(x_0, y_0)} da una retta {r} avente equazione in forma esplicita:

y=mx+q

In questo caso non possiamo applicare la formula precedentemente data, poiché effettivamente non riusciamo a ricavare direttamente i coefficienti {a, b ,c}. Tuttavia, come visto nell’esempio precedente, un’idea può essere quella di ricondurre l’equazione data alla forma implicita:

y=mx+q \quad \Rightarrow \quad y-mx-q=0 \quad \Rightarrow \quad -mx+y-q=0

L’equazione è ora della forma {ax+by+c=0} ed è dunque possibile ricavare i coefficienti {a,b,c}, in modo da poter applicare la formula per il calcolo della distanza retta-punto.

Esempio (distanza retta-punto con equazione della retta in forma esplicita)

Calcolare la distanza tra il punto {P=(-2,-3)} e la retta {r} di equazione in forma esplicita {y=-\dfrac{2}{3}x+\dfrac{4}{5}}.

Cominciamo riconducendo l’equazione della retta {r} alla forma implicita:

y=-\dfrac{2}{3}x+\dfrac{4}{5} \quad \Rightarrow \quad \dfrac{2}{3}x+y-\dfrac{4}{5}=0 \quad \Rightarrow \quad \dfrac{10x+15y-12}{\cancel{15}}=0

Osserviamo che abbiamo ricondotto l’equazione alla forma intera, mettendo tutti i termini a denominatore comune. Precisiamo tra l’altro che è stato possibile eliminare direttamente il denominatore senza alcuna discussione, trattandosi di un numero. Ricondurre l’equazione alla forma intera non è obbligatorio ma comunque fortemente raccomandabile, in quanto semplifica i successivi calcoli relativi all’applicazione della formula distanza punto-retta.

Così abbiamo in definitiva per la retta {r} l’equazione in forma implicita:

r: 10x+15y-12=0

Confrontando tale equazione con la sua forma generica {ax+by+c=0}, ricaviamo immediatamente {a=10, b=15, c=-12}. Essendo inoltre note le coordinate del punto {P}, possiamo a questo punto applicare la formula per il calcolo della distanza punto-retta:

\begin{align*} & d(P,r)=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}=\dfrac{|10 \cdot (-2)
+15 \cdot (-3)+(-12)|}{\sqrt{10^2+15^2}}= \\ \\ & =\dfrac{|-20-45-12|}{\sqrt{100+225}}=\dfrac{|-77|}{\sqrt{325}}=\dfrac{77}{5\sqrt{13}}\end{align*}

Formula per il calcolo della distanza punto-retta con equazione della retta in forma esplicita

Piuttosto che utilizzare l’approccio dell’esercizio precedente (che è comunque quello consigliato), è anche possibile ricavare una formula specifica per il caso del calcolo distanza punto-retta, ove l’equazione della retta sia in forma esplicita.

Riprendiamo per comodità la formula relativa al caso dell’equazione della retta in forma implicita:

 d(P,r)=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}

Supponiamo di dover ricavare la distanza tra il punto {P=(x_0, y_0)} e la retta {r} con equazione data in forma esplicita:

r: y=mx+q

Supponiamo inoltre di non voler ricondurre l’equazione alla forma implicita, ma di volerla utilizzare così come è.

Allo scopo, ricordiamo che si ha:

y=mx+q \quad \Rightarrow y-mx-q=0 \quad \Rightarrow  -mx+y-q=0

da cui {a=-m, b=1, c=-q}.

Di conseguenza, sostituendo le espressioni appena ricavate per i coefficienti {a,b,c} nella formula per il calcolo della distanza di un punto da una retta otteniamo:

\begin{align*} & d(P,r)=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}=\dfrac{|-mx_0+y_0-q|}{\sqrt{(-m)^2+1^2}}=\dfrac{|y_0-(mx_0+q)|}{\sqrt{1+m^2}}\end{align*}

Formula distanza punto-retta con equazione della retta in forma esplicita. Dato un punto {P=(x_0, y_0)} ed una retta {r} di equazione in forma esplicita {y=mx+q}, la distanza tra il punto {P} e la retta {r} è data da:{d(P,r)=\dfrac{|y_0-(mx_0+q)|}{\sqrt{1+m^2}}}

Piuttosto che ricordare anche questa formula, consigliamo come visto in un precedente esempio di ricondurre l’equazione in forma esplicita della retta data alla forma implicita, per poi utilizzare la formula presentata all’inizio della lezione. Tuttavia, abbiamo comunque deciso di fornire entrambe le versioni della formula per un discorso di completezza della trattazione.

A seguire presentiamo un esempio relativo all’utilizzo della formula appena introdotta.

Esempio (formula nella versione con equazione della retta in forma esplicita)

Calcolare la distanza tra il punto {P=(1,5)} e la retta {r} di equazione in forma esplicita {y=\dfrac{1}{2}x-3}.

Si ha:

\begin{align*} &d(P,r)=\dfrac{|y_0-(mx_0+q)|}{\sqrt{1+m^2}}=\dfrac{\left|5-\left[\dfrac{1}{2} \cdot 1+(-3)\right]\right|}{\sqrt{1+\left( \dfrac{1}{2}\right)^2}}= \\ \\ & =\dfrac{\dfrac{15}{2}}{\dfrac{\sqrt{5}}{2}}=\dfrac{15}{2} \cdot \dfrac{2}{\sqrt{5}}=\dfrac{15}{\sqrt{5}}=\dfrac{15}{\sqrt{5}}\cdot \dfrac{\sqrt{5}}{\sqrt{5}}=\dfrac{15 \sqrt{5}}{5}=3\sqrt{5}\end{align*}

Calcolo dell’area di un triangolo qualunque dati i suoi vertici

Un’interessante applicazione della formula per il calcolo della distanza di un punto da una retta del piano è data dal calcolo dell’area di un triangolo qualunque a partire dalle coordinate dei suoi vertici.

Supponiamo di avere un triangolo i vertici del quale abbiano coordinate:

A=(1,2); \quad  B=(3,4); \quad C =(5,1) 

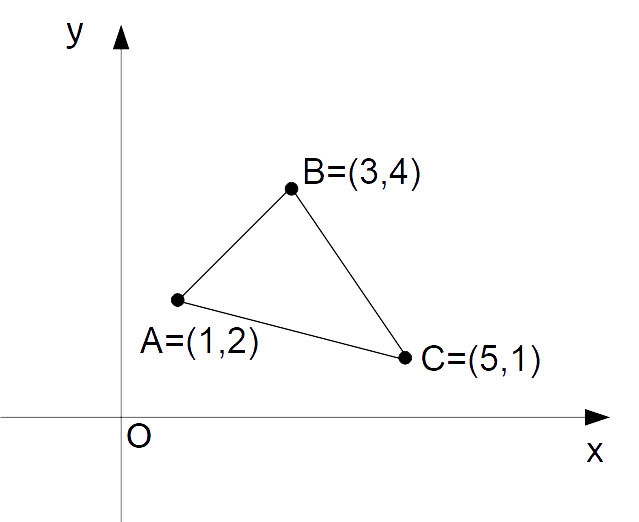
Scegliamo ad esempio il lato {\overline{AC}} come base. A tale lato corrisponde l’altezza {\overline{BH}} che, attenzione, è la distanza del punto {B} dalla retta {r} passante per i punti {A} e {C}. Infatti, per definizione l’altezza del triangolo relativa al lato {\overline{AC}} è misurata lungo la perpendicolare al lato stesso.

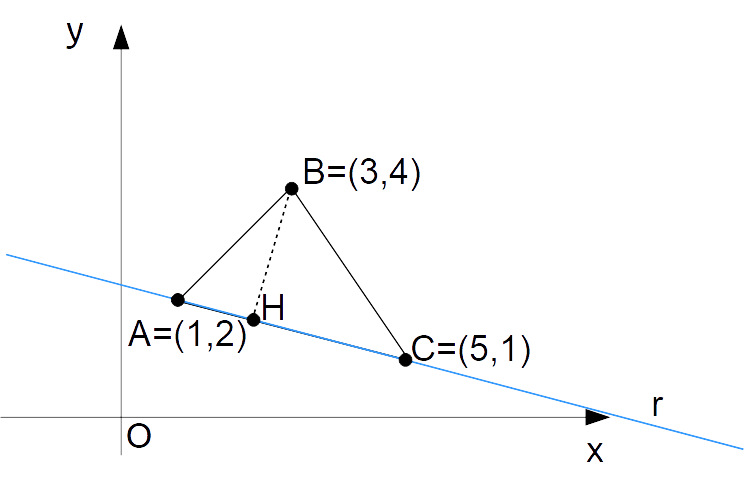
L’area del triangolo è data da:

A=\dfrac{1}{2} \overline{AC} \cdot \overline{BH} 

Per calcolare {\overline{AC}} basta calcolare la distanza tra i due punti {A} e {C}:

\begin{align*} &\overline{AC}=\sqrt{(x_C-x_A)^2+(y_C-y_A)^2}=\sqrt{(5-1)^2+(1-2)^2}=\\ \\ & =\sqrt{4^2+(-1)^2}=\sqrt{16+1}=\sqrt{17}\end{align*}

La misura dell’altezza {\overline{BH}} è invece uguale come anticipato alla distanza del punto {B} rispetto alla retta {r} passante per i punti {A} e {C}. Quest’ultima ha equazione (vedi retta passante per due punti):

\dfrac{y-y_A}{y_C-y_A}=\dfrac{x-x_A}{x_C-x_A} \quad \Rightarrow \quad \dfrac{y-2}{1-2}=\dfrac{x-1}{5-1}

ovvero:

\begin{align*} & 2-y=\dfrac{x-1}{4} \quad \Rightarrow \quad 2-y-\dfrac{x-1}{4}=0 \quad \Rightarrow \quad \\ \\ & \Rightarrow\dfrac{8-4y-x+1}{4}=0 \quad \Rightarrow \quad r:-x-4y+9=0  \end{align*}

La retta {r} ha dunque equazione {-x-4y+9} con {a=-1, b=-4, c= 9}.

Ora non resta che calcolare la distanza tra il punto {B=(x_0, y_0)=(3,4)} e la retta {r}:

\begin{align*} &d(B, r)=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}=\dfrac{|-1 \cdot 3+(-4)\cdot4+9}{\sqrt{(-1)^2+(-4)^2}}=\\ \\ & =\dfrac{|-3-16+9|}{\sqrt{17}}=\dfrac{10}{\sqrt{17}}\end{align*}

Concludiamo calcolando l’area del triangolo:

A = \dfrac{1}{2}\cdot  \overline{AC} \cdot  \overline{BH }=\dfrac{1}{2} \cdot \sqrt{17} \cdot \dfrac{10}{\sqrt{17}}=5

Dimostrazione della formula per il calcolo della distanza di un punto da una retta nel piano (facoltativo)

Proponiamo nel seguito la dimostrazione completa della formula per il calcolo della distanza di un punto da una retta del piano. Ci riferiamo in particolare alla formula relativa al caso in cui l’equazione della retta sia data in forma implicita, e quindi alla prima formula presentata nella lezione. Tuttavia, dimostrando la formula nella prima versione risulterà automaticamente dimostrata anche quella nella seconda versione. Infatti, come visto nel paragrafo precedente quest’ultima si ricava agevolmente dalla prima.

La dimostrazione non è concettualmente difficile, ma ha il solo inconveniente di richiedere lo svolgimento di passaggi a volte un po’ lunghi. Tuttavia, quanto segue costituisce anzitutto un’ottima occasione di ripasso relativamente alla scomposizione dei polinomi, al calcolo delle frazioni algebriche ed alle proprietà dei radicali. E soprattutto, la dimostrazione rappresenta anche un’importante applicazione di una buona parte di quanto sin qui visto sulla geometria analitica (relazione di perpendicolarità tra rette, intersezione tra rette, ecc.). Ma veniamo subito ai dettagli.

Per definizione, la distanza tra un punto {P=(x_0, y_0)} ed una retta {r} nel piano è la più piccola tra le distanze tra ciascun punto della retta e il punto {P}. E tale distanza corrisponde alla distanza presa lungo la retta perpendicolare ad {r} e passante per il punto {P}. Di conseguenza, la distanza tra il punto {P} e la retta {r} è uguale alla distanza tra i due punti {P} e {P'}, ovvero {d(P,r) = |PP'|} (vedi figura a seguire).

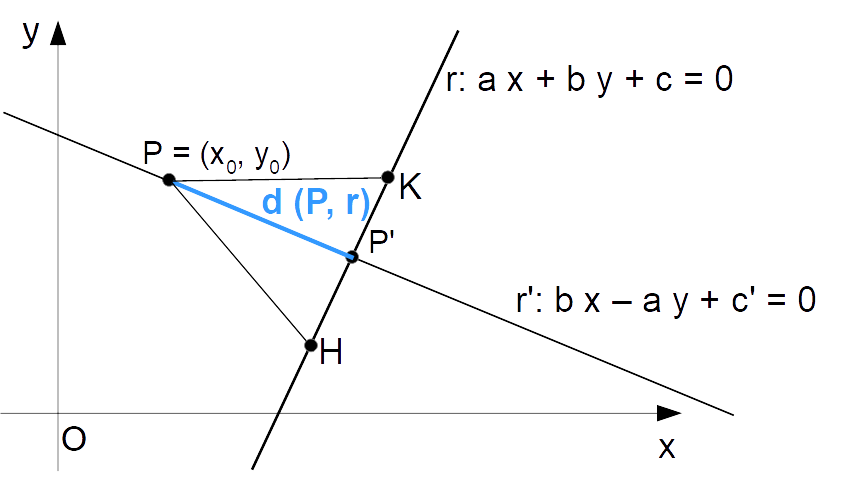
Osserviamo che considerando le distanze tra il punto {P} ed altri punti sulla retta {r}, otteniamo sempre distanze maggiori di {|PP'|}. Ad esempio, le distanze {|PH|} e {|PK|} sono entrambe maggiori di {|PP'|}. Così, soltanto quest’ultima distanza rappresenta effettivamente la distanza tra il punto {P} e la retta {r}, come da definizione.

Ora, se la retta {r} ha equazione (in forma implicita):

r:ax+by+c=0

allora la retta {r'} ad essa perpendicolare ha equazione (vedi rette perpendicolari):

r':bx-ay+c'=0

Ricordiamo infatti che data l’equazione di una retta {r} in forma implicita, l’equazione di una retta ad essa perpendicolare si ottiene scambiando fra loro i coefficienti dei termini in {x} e {y} ed invertendo il segno di uno ed uno solo dei due.

Ora, il punto {P} ha coordinate {x_0} e {y_0} e la retta {r'} passa per il punto {P} stesso. Dovrà quindi essere, sostituendo nell’equazione di {r'} le coordinate del punto {P}:

bx_0-ay_0+c'=0

dalla quale si ricava:

c'=ay_0-bx_0

Pertanto, l’equazione della retta {r'} si può esprimere come:

r': bx-ay+ay_0-bx_0=0

Ora, le coordinate del punto {P'} si ottengono intersecando tra loro la retta {r} e la retta {r'}. E, come sappiamo dalla precedente lezione sull’intersezione tra due rette, tali coordinate si ottengono mettendo a sistema le equazioni rispettivamente della retta {r} e della retta {r'}:

\begin{cases} ax+by+c=0 \\ \\ bx-ay+ay_0-bx_0=0\end{cases}

Risolviamo il sistema (ad esempio per sostituzione), ricordando che la soluzione sarà una coppia del tipo {(x,y)} (i passaggi a seguire sono validi per {a} e {b} entrambi diversi da zero).

\begin{align*} & \begin{cases} x=\dfrac{-by-c}{a}, \qquad a \neq 0 \\ \\ b \cdot \left( \dfrac{-by-c}{a}\right)-ay+ay_0-bx_0=0\end{cases} ;\\ \\ & \begin{cases} x=\dfrac{-by-c}{a} \\ \\ \dfrac{-b^2y-bc}{a}-ay+ay_0-bx_0=0 \end{cases} ; \\ \\ & \begin{cases}\dots \\ \\ \dfrac{-b^2y-bc-a^2y+a^2y_0-abx_0}{a}=0\end{cases}; \\ \\ & \begin{cases} \dots \\ \\ b^2y+a^2y=-bc+a^2y_0-abx_0, \qquad a \neq 0\end{cases}\end{align*}

Proseguiamo i passaggi eseguendo un raccoglimento al primo membro della seconda equazione a sistema (per brevità abbiamo nel frattempo sostituito la prima equazione con dei puntini).

\begin{cases} \dots \\ \\ (a^2+b^2)y=-bc+a^2y_0-abx_0\end{cases}

A questo punto è possibile isolare la {y} nella seconda equazione. Riprendiamo inoltre la prima equazione, riscrivendola nel sistema al posto dei puntini:

\begin{cases}x=\dfrac{-by-c}{a} \\ \\ y=\dfrac{-bc+a^2y_0-abx_0}{a^2+b^2}, \qquad a,b \neq 0\end{cases}

Ora sostituiamo l’espressione ottenuta per {y} nella prima equazione a sistema:

\begin{cases}x=\dfrac{-b\left( \dfrac{-bc+a^2y_0-abx_0}{a^2+b^2}\right)-c}{a} \\ \\ y=\dfrac{-bc+a^2y_0-abx_0}{a^2+b^2}\end{cases}

Semplificando opportunamente il secondo membro della prima equazione (vedi frazioni algebriche):

\begin{align*} & \begin{cases} x=\dfrac{\dfrac{b^2c-a^2by_0+ab^2x_0}{a^2+b^2}-c}{a} \\ \\ y=\dots \end{cases}; \\ \\ & \begin{cases}x = \dfrac{b^2c-a^2by_0+ab^2x_0-c(a^2+b^2)}{(a^2+b^2) \cdot a} \\ \\ y = \dots  \end{cases}; \\ \\ & \begin{cases} x=\dfrac{\cancel{b^2c}-a^2by_0+ab^2x_0-a^2c-\cancel{b^2c}}{a} \cdot \dfrac{1}{a^2+b^2} \\ \\  y=\dots \end{cases}; \\ \\ & \boxed{\begin{cases} x=\dfrac{-aby_0+b^2x_0-ac}{a^2+b^2} \\ \\ y=\dfrac{-bc+a^2y_0-abx_0}{a^2+b^2} \end{cases}}\end{align*}

Abbiamo così ottenuto le coordinate del punto {P'}:

P'=\left(\dfrac{-aby_0+b^2x_0-ac}{a^2+b^2}, \dfrac{-bc+a^2y_0-abx_0}{a^2+b^2}   \right)

Ma arrivati a questo punto, la distanza tra il punto {P} e la retta {r} non è altro che la distanza tra i due punti {P} e {P'}, ovvero {|PP'|}. Di conseguenza, ricordando la formula per il calcolo della distanza tra due punti nel piano, si ha:

\small \begin{align*} &| PP'|=\sqrt{\left( x_{P'}-x_P\right)^2+\left(y_{P'}-y_P\right)^2}= \\ \\ & =\sqrt{\left(\dfrac{-aby_0+b^2x_0-ac}{a^2+b^2}-x_0 \right)^2+\left(  \dfrac{-bc+a^2y_0-abx_0}{a^2+b^2}  -y_0\right)^2}=\\ \\ & =\sqrt{\left(\dfrac{-aby_0+\cancel{b^2x_0}-ac-a^2x_0-\cancel{b^2x_0}}{a^2+b^2}\right)^2+\left( \dfrac{-bc+\cancel{a^2y_0}-abx_0-\cancel{a^2y_0}-b^2y_0}{a^2+b^2}\right)^2}= \\ \\ & =\sqrt{\dfrac{\left( -aby_0-ac-a^2x_0\right)^2}{(a^2+b^2)^2}+\dfrac{\left( -bc-abx_0-b^2y_0\right)^2}{(a^2+b^2)^2}}= \end{align*}

Osserviamo che nell’ultimo passaggio abbiamo sfruttato la proprietà della potenza di una frazione. In generale si ha, infatti {\left( \dfrac{a}{b}\right)^2=\dfrac{a^2}{b^2}}.

Nel proseguire i passaggi, basta ridurre a denominatore comune i termini all’interno del simbolo di radice, sviluppando i quadrati di trinomi al numeratore:

\tiny=\sqrt{\dfrac{a^2b^2y_0^2+a^2c^2+a^4x_0^2+2a^2bcy_0+2a^3bx_0y_0+2a^3cx_0+b^2c^2+a^2b^2x_0^2+b^4y_0^2+2ab^2cx_0+2b^3cy_0+2ab^3x_0y_0}{(a^2+b^2)^2}}=

Ora il trucco sta nel raccogliere parzialmente i termini a numeratore per i fattori {a^2} e {b^2}, ed a ciò faremo seguire un opportuno raccoglimento a fattore comune totale:

\begin{align*} &\tiny=\sqrt{\dfrac{a^2\left(b^2y_0^2+c^2+a^2x_0^2+2bcy_0+2abx_0y_0+2acx_0\right)+b^2\left(c^2+a^2x_0^2+b^2y_0^2+2acx_0+2bcy_0+2abx_0y_0\right)}{(a^2+b^2)^2}}=\\ \\ & =\sqrt{\dfrac{\left( b^2y_0^2+c^2+a^2x_0^2+2bcy_0+2abx_0y_0+2acx_0\right)\cancel{ \left( a^2+b^2\right)}}{(a^2+b^2)^{\cancel{2}}}} =\end{align*}

Riconoscendo il quadrato di un trinomio al numeratore e concludendo i passaggi grazie alle proprietà dei radicali si ha infine:

=\sqrt{\dfrac{(by_0+c+ax_0)^2}{a^2+b^2}}=\dfrac{\sqrt{(by_0+c+ax_0)^2}}{\sqrt{a^2+b^2}}=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}

da cui in definitiva otteniamo la formula per il calcolo della distanza del punto {P=(x_0,y_0)} rispetto alla retta {r:ax+by+c=0}:

|PP'|=d(P, r)=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}

e ciò è quanto volevamo dimostrare.

Come calcolare la distanza di un punto da una retta del piano senza ricordare le formule

Se dobbiamo calcolare la distanza tra un punto ed una retta del piano ma non ricordiamo le formule, nessun problema. E’ possibile comunque effettuare il calcolo seguendo un procedimento del tutto simile a quello utilizzato per ricavare la formula della distanza punto-retta (vedi il paragrafo precedente).

In particolare, dati un punto {P(x_0, y_0)} e data una retta {r:ax+by+c=0}, basterà seguire i seguenti passaggi:

• scrivere l’equazione della retta perpendicolare ad {r} e tale da passare per il punto {P};
• determinare le coordinate del punto {P'}, che è il punto di intersezione tra il punto {P} e la retta {r};
• infine, calcolare la distanza tra il punto {P} e il punto {P'}, ottenendo così la distanza punto-retta cercata.

Esempio

Calcolare la distanza del punto {P=(-1,-3)} dalla retta {r: 2x+3y-7=0} senza utilizzare la formula per la distanza punto-retta.

Cominciamo scrivendo l’equazione della retta {r'} tale da essere perpendicolare ad {r} e tale da passare per il punto {P}. L’equazione di una retta perpendicolare ad {r'} è della forma:

s: 3x-2y+c' = 0

ove {c'} è un opportuno numero reale. Imponendo la condizione di appartenenza della retta {s} al punto {P} otteniamo:

\small 3x_0-2y_0+c'=0 \quad \Rightarrow \quad c'=-3x_0+2y_0=-3(-1)+2(-3)=-3

Di conseguenza essendo {c'=-3} l’equazione della retta {r'} si ottiene a partire dall’equazione della generica retta {s} perpendicolare a {r} sostituendo il valore appena ottenuto per {c'}:

r'=3x-2y-3

Ora determiniamo le coordinate del punto di intersezione tra le rette {r} ed {r'} mettendo a sistema le corrispondenti equazioni:

\begin{cases} 2x+3y-7=0 \\ \\ 3x-2y-3=0 \end{cases}

Risolvendo il sistema ad esempio per sostituzione otteniamo:

\scriptsize  \begin{cases} 6x+9y-21=0  \\ \\ -6x+4y+6=0\end{cases} \quad \Rightarrow \begin{cases} 13y-15=0 \quad \rightarrow y= \dfrac{15}{13}\\ \\ -6x+4y+6=0 \quad \rightarrow x=\dfrac{4\cdot \dfrac{15}{13}+6}{6}=\dfrac{23}{13}\end{cases}

Di conseguenza il punto {P'} intersezione delle rette {r} ed {r'} ha coordinate:

P'=\left(\dfrac{23}{13}, \dfrac{15}{13}\right)

Ora non rimane che calcolare la distanza {|PP'|}:

\begin{align*} &|PP'|=\sqrt{(x_{P'}-x_0)^2+(y_{P'}-y_0)^2}= \\ \\ & =\sqrt{\left( \dfrac{23}{13}+1\right)^2+\left( \dfrac{15}{13}+3\right)^2}=\sqrt{\left( \dfrac{36}{13}\right)^2+\left( \dfrac{54}{13}\right)^2}=\\ \\ & =\sqrt{\dfrac{1296+2916}{169}} =\sqrt{\dfrac{4212}{169}}\end{align*}

In questo caso non converrebbe semplificare il risultato, anche se ciò è possibile. Con un po’ di fatica si ha comunque:

\begin{align*} & \sqrt{\dfrac{4212}{169}}=\dfrac{\sqrt{4212}}{\sqrt{13^2}}=\dfrac{\sqrt{4212}}{13}=\dfrac{\sqrt{1053 \cdot 2^2}}{13}= \\ \\ & =\dfrac{\sqrt{3^4 \cdot 13 \cdot 2^2}}{13}=\dfrac{9 \cdot 2\sqrt{13}}{13}=\dfrac{18\sqrt{13}}{13}\end{align*}

Abbiamo così ottenuto la distanza tra il punto {P} e la retta {r} dati.

Vediamo come verifica se utilizzando la formula ritroviamo il risultato appena scritto:

\begin{align*} &d(P,r)= \dfrac{|ax_0+by_0+c}{\sqrt{a^2+b^2}}=\dfrac{|2 (-1)+3(-3)-7}{\sqrt{2^2+3^2}}=\\ \\ & =\dfrac{|-2-9-7|}{\sqrt{13}}=\dfrac{18}{\sqrt{13}} \cdot \dfrac{\sqrt{13}}{\sqrt{13}}=\dfrac{18 \sqrt{13}}{13}\end{align*}

Tale risultato effettivamente corrisponde a quello ottenuto in precedenza.

Conclusioni

Per quanto riguarda la formula per il calcolo della distanza di un punto da una retta del piano è tutto. Nella prossima lezione ci occuperemo dei fasci di rette, sia propri, sia impropri. E questa sarà l’ultima lezione relativa alle rette del piano cartesiano.

Buon proseguimento con SìMatematica!