Esercizi sull’intersezione di due rette

 - 

Esercizi sulla retta nel piano e coordinate cartesiane

Proponiamo una serie di esercizi svolti sull’intersezione di due rette, l’obiettivo dei quali è quello di determinare le coordinate del punto di intersezione tra due rette del piano cartesiano.

Come già sappiamo dalla lezione teorica, per svolgere gli esercizi sull’intersezione di due rette occorre risolvere un opportuno sistema lineare (sistema di equazioni di primo grado). In particolare, ci ritroveremo a dover risolvere un sistema nel quale figurano le equazioni corrispondenti alla due rette delle quali cerchiamo l’eventuale punto di intersezione. Così, per svolgere gli esercizi sull’intersezione di due rette è fondamentale ricordare i metodi risolutivi dei sistemi lineari.

Facendo un breve richiamo, date le due rette del piano, con equazioni in forma esplicita:

r_1:y=m_1x+q_1, \qquad r_2: y=m_2x+q_2

l’idea è quella di risolvere il sistema:

\begin{cases} y=m_1x+q_1 \\ \\ y=m_2x+q_2\end{cases}

In questo caso il metodo più indicato per risolvere un sistema in questa forma è il metodo del confronto. Infatti, le equazioni a sistema sono in forma esplicita e ci ritroviamo quindi con due espressioni per l’incognita {y}, che possiamo uguagliare tra loro. In tal modo, è possibile ricondurre una delle due equazioni a sistema ad un’equazione nella sola incognita {x}.

Se invece le equazioni delle rette sono date in forma implicita:

r_1=a_1x+b_1y+c_1=0, \qquad r_2:a_2x+b_2y+c_2=0

ci ritroviamo con il sistema:

\begin{cases} a_1x+b_1y+c_1=0 \\ \\ a_2x+b_2y+c_2=0\end{cases}

In questo caso il metodo che ci sentiamo di consigliare per risolvere il sistema in esame è il metodo di riduzione.

Quando si è di fronte agli esercizi sull’intersezione tra due rette, è importante ricordare che non è detto che il punto di intersezione tra le due rette date esista. In altre parole, le due rette potrebbero anche non intersecarsi tra loro. In particolare, in base al fatto che il sistema lineare possa essere determinato, indeterminato o impossibile ci ritroviamo con i seguenti casi:

• sistema determinato: esiste un unico punto di intersezione tra le due rette, le quali risultano incidenti;
• sistema indeterminato: esistono infiniti punti di intersezione tra le due rette, le quali sono coincidenti;
• infine, sistema impossibile: non esiste alcun punto di intersezione tra le due rette, le quali risultano parallele e distinte (o se preferite, parallele non coincidenti).

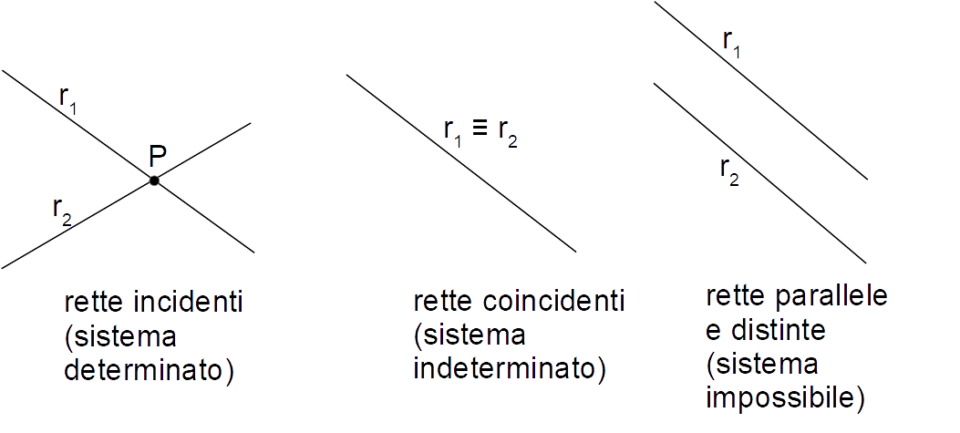
Fatti i dovuti richiami, procediamo subito con gli esercizi sull’intersezione tra due rette. E precisiamo che ci occuperemo anche dei casi particolari di rette con equazioni date l’una in forma esplicita e l’altra in forma implicita. In tali circostanze, come vedremo tra pochi istanti, risulterà conveniente ricondurre entrambe le equazioni o alla forma esplicita, o alla forma implicita.

Prima parte: esercizi sull’intersezione tra due rette con equazioni nella stessa forma

Esercizio 1

Determinare l’eventuale punto di intersezione tra le rette {r_1: x-y=1} e {r_2: x+2y=4}.

Cominciamo mettendo a sistema le equazioni delle rette:

\begin{cases} x-y=1 \\ \\ x+2y=4\end{cases}

Osserviamo che data la particolare forma delle equazioni il sistema è in forma normale. Di conseguenza può essere direttamente risolto con qualunque metodo, anche compreso il metodo di Cramer.

Nel caso in esame appare comodo applicare il metodo di riduzione. Sostituiamo allora una delle due equazioni a sistema con una nuova equazione che si ottiene sottraendo membro a membro ad esempio la seconda equazione alla prima. Mettiamo l’equazione che così otteniamo al posto ad esempio della prima equazione.

\begin{cases} -3y=-3  \\ \\ x+2y=4\end{cases}

La prima equazione a sistema è ora nella sola incognita {y}. Per cui è possibile ricavare il valore della {y} dalla prima equazione, e quindi sostituirlo nella seconda equazione, in modo da ricavare il valore anche dell’incognita {x}:

\begin{cases} y=1 \\ \\ x=4-2 \cdot 1 = 2\end{cases}

Così il sistema ha per soluzione la coppia {(x,y)=(2,1)}. E ciò in termini geometrici significa che le due rette date si intersecano nel punto {P=(2,1)}.

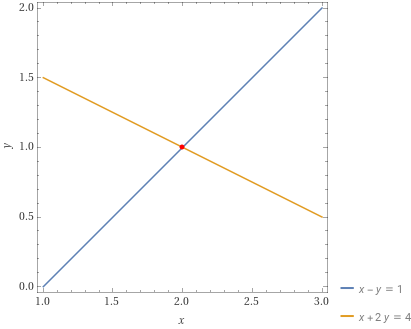
Quindi in conclusione le rette sono incidenti ed hanno come punto di intersezione il punto {P=(2,1)}.

Graficamente abbiamo la seguente rappresentazione:

Esercizio 2

Proseguiamo questa serie di esercizi sull’intersezione tra due rette con il seguente, nel quale vedremo come applicare la regola di Cramer.

Determinare l’eventuale punto di intersezione tra le due rette {r_1:6x-5y+2=0} e {r_2:2x+3y-4=0}.

Cominciamo anzitutto scrivendo il sistema da risolvere:

\begin{cases} 6x-5y+2=0 \\ \\ 2x+3y-4=0 \end{cases}

Il sistema non è in forma normale. Infatti, i termini noti non si trovano al secondo membro. Di conseguenza, non è possibile applicare direttamente il metodo di Cramer. Tuttavia, per farlo basterà trasportare i termini noti al secondo membro:

\begin{cases} 6x-5y=-2 \\ \\ 2x+3y=4\end{cases}

Ora il sistema è in forma normale, in quanto i termini noti compaiono soltanto al secondo membro e in nessuna equazione figurano termini simili.

A questo punto possiamo scegliere tra il metodo di riduzione e il metodo di Cramer. Escludiamo i metodi di sostituzione e del confronto poiché il primo risulta troppo laborioso, mentre il secondo non si presta per la forma con la quale si presentano le equazioni a sistema.

Dato che nel precedente esercizio abbiamo utilizzato il metodo di riduzione, vediamo come operare con il metodo di Cramer. Cominciamo scrivendo la matrice dei coefficienti, procedendo poi al calcolo del suo determinante, {D}:

\begin{pmatrix} 6 & -5 \\ 2 & 3\end{pmatrix}

\det \begin{pmatrix} 6 & -5 \\ 2 & 3\end{pmatrix}=6 \cdot 3 - 2 \cdot (-5)=18+10=28

Ora, abbiamo bisogno dei determinanti {D_x} e {D_y}, i quali sono i determinanti, rispettivamente, della matrice che si ottiene sostituendo alla prima colonna della matrice dei coefficienti la colonna dei termini noti e della matrice che si ottiene sostituendo invece alla seconda colonna della matrice dei coefficienti la colonna dei termini noti.

Ricordiamo che la colonna dei termini noti è data dai termini noti di ciascuna equazione nell’ordine in cui si presentano nel sistema.

Così per il determinante {D_x} abbiamo:

D_x = \det \begin{pmatrix} -2 & -5 \\ 4 & 3\end{pmatrix}=-2 \cdot 3 - 4 \cdot (-5)=-6+20=14

Infine, per il determinante {D_y}:

D_y=\det \begin{pmatrix} 6 & -2 \\ 2 & 4\end{pmatrix}=6 \cdot 4 - 2 \cdot (-2)=24+4=28

Ora non resta che ricordare le formule:

x=\dfrac{D_x}{D}, \qquad y=\dfrac{D_y}{D}

ovvero, nel nostro caso:

x=\dfrac{D_x}{D}=\dfrac{14}{28}=\dfrac{1}{2}, \qquad y=\dfrac{D_y}{D}=\dfrac{28}{28}=1

Così in conclusione il sistema è determinato ed ha per soluzione la coppia:

(x,y)=\left( \dfrac{1}{2}, 1\right)

Di conseguenza la due rette sono incidenti ed hanno per punto di intersezione:

P=\left( \dfrac{1}{2}, 1\right)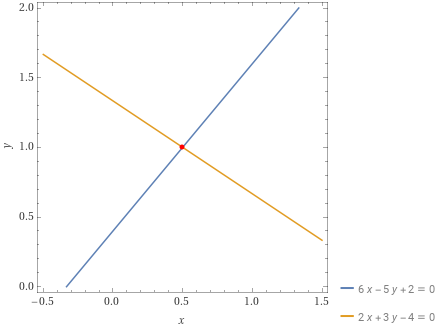

Osserviamo comunque che con il metodo di riduzione avremmo potuto risolvere il problema in maniera più spedita. Riprendiamo allora il sistema di partenza e mostriamo come avremmo potuto procedere, in alternativa, utilizzando il metodo di riduzione.

\begin{cases} 6x-5y+2=0 \\ \\ 2x+3y-4=0 \end{cases}

Osserviamo anzitutto che utilizzando il metodo di riduzione non è necessario ricondurre il sistema alla forma normale. L’importante è che non vi siano termini simili e che i termini nelle stesse incognite e/o i termini noti si trovino tutti allo stesso membro. Così nel nostro caso possiamo direttamente applicare il metodo di riduzione.

Poiché dobbiamo eliminare un’incognita, cominciamo moltiplicando ad esempio tutti i termini della seconda equazione per {-3}:

\begin{cases}  6x-5y+2=0  \\ \\-6x-9y+12=0 \end{cases}

Ora è evidente che se sommiamo tra loro le due equazioni membro a membro, otteniamo una nuova equazione nella sola incognita {y}. Decidendo di sostituire tale nuova equazione alla seconda equazione attualmente a sistema, abbiamo:

\begin{cases} 6x-5y+2=0 \\ \\ -14y+14=0 \quad \rightarrow \quad y=1\end{cases}

e quindi:

\begin{cases} 6x=5y-2 \quad \rightarrow \quad 6x=5 \cdot 1 - 2 \quad \rightarrow \quad x=\dfrac{1}{2}\\ \\  y=1\end{cases}

Di conseguenza ritroviamo ancora come risultato il punto di intersezione:

P=\left( \dfrac{1}{2}, 1\right)

Vista l’immediatezza del metodo di riduzione, negli esercizi a seguire sull’intersezione tra due rette proporremo unicamente tale metodo.

Esercizio 3

Determinare l’eventuale punto di intersezione tra le due rette {r_1: 2x+1=0} e {r_2:x+3y-4=0}.

Scriviamo prima di tutto il sistema da risolvere:

\begin{cases} 2x+1=0 \\ \\  x+3y-4=0\end{cases}

Osserviamo che la prima equazione è già in una sola incognita. Infatti, la retta:

r_1: 2x+1=0

è una retta verticale. Infatti, esplicitando la {x}:

r_1:x=-\dfrac{1}{2}

Ci ritroviamo così con un’equazione della forma {x=k, \: k \in \R}, che è relativa ad una retta verticale.

Così abbiamo per il sistema:

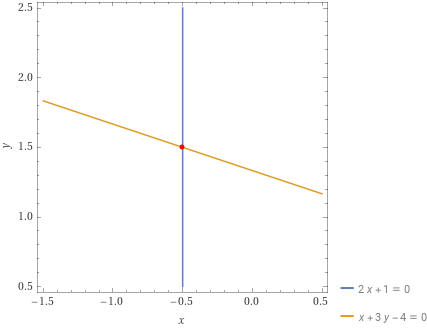
\begin{cases} x=-\dfrac{1}{2} \\ \\ -\dfrac{1}{2}+3y-4=0 \quad \rightarrow \quad 3y=4+\dfrac{1}{2} \quad \rightarrow y=\dfrac{4}{3}+\dfrac{1}{6}=\dfrac{3}{2}\end{cases}

Di conseguenza le due rette sono incidenti ed hanno come punto di intersezione:

P=(x,y)=\left( -\dfrac{1}{2}, \dfrac{3}{2}\right)

Possiamo rappresentare graficamente l’intersezione tra le due rette date come segue:

Esercizio 4

Determinare le coordinate dell’eventuale punto di intersezione tra le rette {r_1: y=-2x+5} e {r_2: y=-\dfrac{3}{5}x+\dfrac{4}{5}}.

Mettiamo entrambe le equazioni delle rette a sistema:

\begin{cases} y=-2x+5 \\ \\ y=-\dfrac{3}{5}x+\dfrac{4}{5}\end{cases}

Poiché entrambe le equazioni si presentano nella forma esplicita, per risolvere il sistema è conveniente utilizzare il metodo del confronto. Richiamando brevemente il metodo, l’idea è quella di uguagliare tra loro i secondi membri delle equazioni a sistema. In tal modo si ottiene una nuova equazione in una sola incognita che è possibile sostituire ad una delle due equazioni a sistema (ad esempio, la seconda). Così abbiamo:

\begin{cases}y=-2x+5\\ \\  -2x+5=-\dfrac{3}{5}x+\dfrac{4}{5} \end{cases}

Ricavando la {x} dalla seconda equazione:

\begin{cases}y=-2x+5\\ \\  -2x+5=-\dfrac{3}{5}x+\dfrac{4}{5} \quad \rightarrow \quad x=3 \end{cases}

Ora non resta che ricavare il valore della {y} per sostituzione:

\begin{cases} y=-1 \\ \\ x=3\end{cases}

Così il sistema risulta determinato e di conseguenza le due rette sono incidenti. Il loro punto di intersezione è:

P=(3,-1)

Come mostra l’esercizio appena svolto, il metodo del confronto è un utile strumento per la risoluzione degli esercizi sull’intersezione tra due rette.

Seconda parte: esercizi sull’intersezione tra due rette non incidenti

Esercizio 5

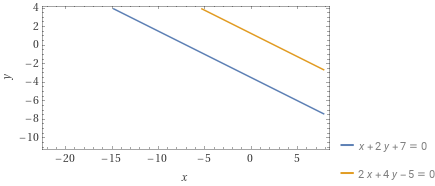
Determinare le coordinate dell’eventuale punto di intersezione tra le rette {r_1: x+2y+7=0} e {r_2: 2x+4y-5=0}.

Come al solito impostiamo il sistema:

\begin{cases} x+2y+7=0 \\ \\ 2x+4y-5=0 \end{cases}

Proviamo a risolvere il sistema per riduzione:

\begin{cases} -2x-4y-14=0 \\ \\ 2x+4y-5=0 \end{cases} \quad \Rightarrow \quad \begin{cases} -19=0 \\ \\ 2x+4y-5=0\end{cases}

Poiché l’uguaglianza numerica {-19=0} è falsa, il sistema è impossibile. Di conseguenza, non esiste alcun punto di intersezione tra le due rette, le quali sono in conclusione parallele non coincidenti.

Osserviamo che ciò era prevedibile anche senza provare a risolvere il sistema. Infatti, esaminando le equazioni di partenza possiamo rilevare che i coefficienti dei termini in {x} e {y} sono tra loro proporzionali. In altre parole, il rapporto tra i coefficienti dei termini in {x} è uguale al rapporto tra i coefficienti dei termini in {y} (presi ordinatamente).

Ricordiamo infatti in generale che le due equazioni {r_1:a_1x+b_1y+c_1=0} e {a_2x+b_2y+c_2=0} corrispondono a due rette tra loro parallele se e solo se:

\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}

Nel nostro caso:

\dfrac{1}{2}=\dfrac{2}{4}

uguaglianza evidentemente verificata. Quindi le due rette sono parallele. Ma sono coincidenti oppure no?

Per fare quest’ultima verifica, basta controllare se le due rette hanno ordinate all’origine uguali oppure no. Ricordiamo che l’ordinata all’origine di una retta con equazione della forma {ax+by+c=0} si ottiene come {q=-\dfrac{c}{b}}.

Così, nel nostro caso abbiamo rispettivamente:

q_1=-\dfrac{c_1}{b_1}=-\dfrac{7}{2}; \qquad q_2=-\dfrac{c_2}{b_2}=-\dfrac{-5}{4}=\dfrac{5}{4}

Quindi, le due rette hanno differente ordinata all’origine, e pertanto non possono certamente essere coincidenti.

Così in conclusione le due rette risultano parallele non coincidenti, e quindi prive di punti di intersezione.

Esercizio 6

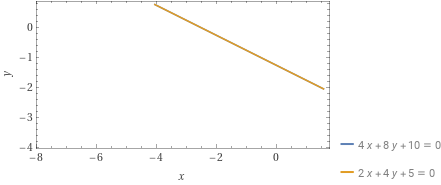
Trovare l’eventuale punto di intersezione tra le due rette {r_1: 4x+8y+10=0} e {r_2: 2x+4y+5=0}.

Osserviamo che utilizzando il secondo principio di equivalenza è possibile ricondurre l’equazione della retta {r_1} alla stessa forma dell’equazione della retta {r_2}. Basta infatti dividere tutti i termini dell’equazione di {r_1} per {2}.

Così in conclusione le due rette hanno la stessa equazione e sono di conseguenza parallele e coincidenti.

Si può arrivare alla stessa conclusione anche osservando che le due rette hanno i coefficienti dei termini in {x} e {y} rispettivamente proporzionali tra loro (rette parallele) ed hanno le stesse ordinate all’origine (rette coincidenti). Così ritroviamo ancora il risultato che le due rette sono parallele e coincidenti.

Così, in conclusione, le due rette hanno tra loro infiniti punti di intersezione.

Ora, cosa sarebbe successo se avessimo provato a mettere a sistema le equazioni delle due rette di partenza? Abbiamo:

\begin{cases} 4x+8y+10=0 \\ \\ 2x+4y+5=0 \end{cases}

Utilizziamo il metodo di riduzione:

\begin{cases} 4x+8y+10=0 \\ \\ -4x-8y-10=0\end{cases} \quad \Rightarrow \quad \begin{cases} 4x+8y+10=0 \\ \\0=0\end{cases}

Poiché abbiamo a sistema l’identità {0=0} il sistema è indeterminato, ed ha quindi infinite soluzioni. Di conseguenza, troviamo ulteriore conferma del fatto che le due rette hanno infiniti punti di intersezione, e quindi sono parallele e coincidenti.

Terza parte: esercizi sull’intersezione tra due rette con equazioni in differenti forme

Esercizio 7

Trovare l’eventuale punto di intersezione tra le rette {r_1:6x-10y+1=0} e {r_2:y=\dfrac{1}{2}x+\dfrac{1}{8}}.

E’ qui importante notare che le due equazioni sono scritte in forme differenti. In particolare, l’equazione della retta {r_1} è in forma implicita, mentre l’equazione della retta {r_2} è in forma esplicita. Così, per poter mettere conveniente a sistema le due equazioni è necessario ricondurle entrambe alla forma esplicita o alla forma implicita.

Scegliamo ad esempio di ricondurre l’equazione della retta {r_2} alla forma implicita. Abbiamo (vedi passaggio dalla forma esplicita alla forma implicita):

y=\dfrac{1}{2}x+\dfrac{1}{8} \quad \Rightarrow \quad \dfrac{1}{2}x-y+\dfrac{1}{8}=0 \quad \Rightarrow \quad r_2:4x-8y+1=0

Ora mettiamo a sistema le equazioni delle due rette, utilizzando ovviamente per l’equazione di {r_2} la forma appena ottenuta:

\begin{cases}6x-10y+1=0 \\ \\  4x-8y+1=0 \end{cases}

Moltiplichiamo per {\dfrac{4}{6}} tutti i termini della prima equazione:

\begin{cases}4x-\dfrac{20}{3}y+\dfrac{4}{6} =0 \\ \\ 4x-8y+1=0\end{cases}

A questo punto sostituiamo alla prima equazione a sistema una nuova equazione che si ottiene sottraendo la seconda equazione attualmente a sistema alla prima:

\begin{cases} \left( -\dfrac{20}{3}+8\right)y+\dfrac{4}{6}-1=0 \\ \\ 4x-8y+1=0\end{cases}

Svolgendo i calcoli relativamente alla prima equazione:

\begin{cases} \dfrac{4}{3}y-\dfrac{1}{3}=0 \quad \rightarrow \quad y=\dfrac{1}{4} \\ \\ 4x-8y+1=0 \quad \Rightarrow \quad x=\dfrac{1}{4}\end{cases}

Il sistema è così determinato e le due rette hanno come punto di intersezione:

P=\left( \dfrac{1}{4}, \dfrac{1}{4}\right)

Esercizio 8

Trovare l’eventuale punto di intersezione tra le due rette {r_1: y=-\dfrac{1}{2}x+1 } e {r_2: 3x+y+1=0}.

Anche in questo caso, le due equazioni sono scritte in forma differente. Infatti, l’equazione della retta {r_1} è in forma esplicita mentre l’equazione della retta {r_2} è in forma implicita. In alternativa al metodo utilizzato nell’esercizio precedente, intendiamo ora ricondurre entrambe le equazioni alla forma esplicita.

Si tratterà così di ricondurre l’equazione della retta {r_2} alla forma esplicita. Abbiamo:

3x+y+1=0 \quad \Rightarrow \quad r_2: y=-3x-1

Ora mettiamo a sistema le equazioni delle due rette, utilizzando ovviamente per {r_2} l’ultima forma scritta:

\begin{cases} y=-\dfrac{1}{2}x+1 \\ \\  y=-3x-1 \end{cases}

Applicando il metodo del confronto otteniamo:

\small \begin{cases} -\dfrac{1}{2}x+1=-3x-1 \\ \\  y=-3x-1 \end{cases} \quad \Rightarrow \quad \begin{cases} \dfrac{5}{2}x=-2 \quad \rightarrow \quad x=-\dfrac{4}{5} \\ \\ y=-3\left( -\dfrac{4}{5}\right)-1 \quad \rightarrow \quad y=\dfrac{7}{5}\end{cases}

Così in conclusione le due retta hanno per punto di intersezione:

P=\left( -\dfrac{4}{5} , \dfrac{7}{5}\right)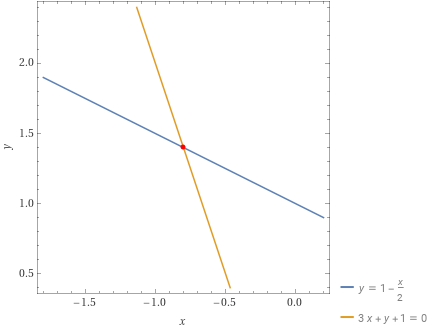

Esercizio 9

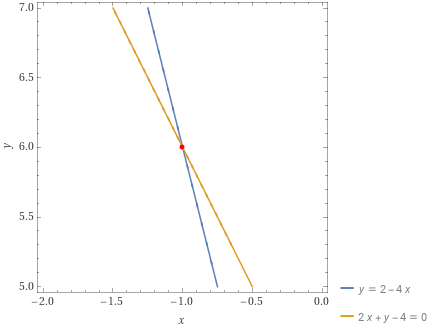
Determinare l’eventuale punto di intersezione tra le rette {r_1: y=-4x+2} e {r_2: 2x+y-4=0}.

Dato che nell’equazione della retta {r_2} il coefficiente del termine in {y} è {1}, appare particolarmente comodo ricondurre quest’ultima equazione alla forma esplicita. In tal modo, entrambe le equazioni di {r_1} ed {r_2} risulteranno espresse in forma esplicita, potendo così applicare il metodo del confronto.

2x+y-4=0 \quad \Rightarrow \quad r_2: y=-2x+4

Mettiamo a sistema le equazioni delle rette, utilizzando per {r_2} l’equazione in forma esplicita appena scritta:

\begin{cases} y=-2x+4 \\ \\ y=-4x+2\end{cases}

A questo punto, sostituiamo ad esempio la prima equazione a sistema con una nuova equazione nella sola incognita {x}, che si ottiene uguagliando tra loro i due secondi membri delle equazioni attualmente a sistema. Abbiamo:

\begin{cases} -2x+4=-4x+2 \\ \\ y=-4x+2\end{cases}

E’ ora possibile ricavare la {x} dalla prima equazione, e quindi per sostituzione ricavare la {y} dalla seconda.

\begin{cases} 2x=-2 \quad \rightarrow \quad x=-1 \\ \\ y=-4 \cdot (-1)+2=6\end{cases}

Così in definitiva le due rette si intersecano tra loro nel punto:

P=(-1,6)

Conclusioni

Per questa serie di esercizi sull’intersezione tra due rette è tutto. Come è evidente, ricordare come risolvere i sistemi lineari, in particolare con i metodi di riduzione e del confronto, è la chiave per poter svolgere questo tipo di esercizi. E per poter comprendere in ogni caso ciò che sta succedendo, è fondamentale ricordare sempre che se il sistema è determinato le rette sono incidenti, se il sistema è indeterminato le rette sono parallele coincidenti, e infine se il sistema è impossibile le rette sono parallele non coincidenti.

Un saluto a tutti voi e buon proseguimento con SìMatematica! 🙂