In questa lezione vediamo ancor più nel dettaglio come si utilizza il metodo di Cramer (o regola di Cramer) per risolvere i sistemi lineari di due o più equazioni in due o più incognite. Vedremo in particolare come risolvere grazie a questo metodo sistemi lineari fino a tre equazioni in tre incognite.
Come già evidenziato nella prima lezione sui sistemi lineari, il metodo di Cramer richiede la conoscenza dei concetti di matrice e determinante. In particolare, il calcolo dei determinanti è l’unica parte “delicata” del metodo di Cramer. Per il resto le procedure da seguire sono piuttosto meccaniche. Anche il calcolo dei determinanti di per sé è un insieme di operazioni puramente algebriche, ma come già sappiamo nell’avere a che fare con l’algebra occorre prestare particolarmente attenzione al segno delle quantità. Ed è questo probabilmente l’aspetto che più può essere fonte di errori nel calcolo dei determinanti. Tuttavia, non è il caso di preoccuparsi poiché il calcolo dei determinanti delle matrici è una procedura che si basa sulle operazioni con i numeri relativi, argomento ben noto sin dalle scuole medie.
Vediamo allora subito nel dettaglio e per passi successivi come risolvere i sistemi lineari utilizzando la regola di Cramer (o metodo di Cramer). Cominceremo dal semplice caso dei sistemi due per due (ovvero i sistemi di due equazioni in due incognite).
Risolvere i sistemi lineari con due equazioni in due incognite utilizzando il metodo di Cramer
La prima cosa della quale dobbiamo parlare nell’introdurre il metodo di Cramer è la definizione di sistema lineare in forma normale.
Un sistema lineare si dice in forma normale se:
- in ciascuna equazione del sistema non compaiono termini tra loro simili. In altre parole, tutti i termini simili sono stati sommati tra loro;
- al primo membro abbiamo solo termini contenenti le incognite, mentre al secondo membro abbiamo i soli termini noti (numeri senza lettere);
- le lettere delle incognite si presentano in ciascuna equazione in ordine alfabetico da sinistra verso destra;
- tutti i coefficienti delle incognite compaiono esplicitamente, compresi i coefficienti uguali a zero (i coefficienti uguali a 1 possono invece essere anche omessi).
L’ultimo punto non è in realtà fondamentale per la definizione di sistema lineare in forma normale, ma deve essere obbligatoriamente seguito per poter applicare correttamente la regola di Cramer.
Un sistema lineare di due equazioni in due incognite in forma normale si scrive in generale come:
\begin{cases} a_1x+b_1y=k_1 \\ \\ a_2x+b_2y=k_2\end{cases}ove {a_1, \: a_2, \: } sono i coefficienti dell’incognita {x}, {b_1, \: b_2} sono i coefficienti dell’incognita {y} e {k_1, \: k_2 } sono i termini noti.
Così, dato il seguente sistema con due equazioni in due incognite:
\begin{cases} 2x=-y-10 \\ \\ x+5y-3 = 0\end{cases}ci accorgiamo immediatamente che questo non è in forma normale. Infatti nella prima equazione, al secondo membro compare non solo un termine noto ma anche un termine contenente l’incognita. Inoltre al primo membro della seconda equazione abbiamo un termine noto al primo membro.
Per ridurre il sistema alla forma normale dobbiamo allora trasportare opportunamente i termini nelle equazioni che compongono lo stesso sistema. Abbiamo:
\begin{cases} 2x+y=-10 \\ \\ x+5y=3\end{cases}E’ appena il caso di ricordare che nel trasportare i termini da un membro all’altro di un’equazione occorre cambiarne il segno.
Ora il sistema è in forma normale. Questo, lo sottolineiamo ancora, è il primo passo per poter applicare la regola di Cramer.
A questo punto, introduciamo la definizione di matrice dei coefficienti. Si tratta di una particolare tabella, quindi un oggetto formato da righe e colonne. In particolare, in tale matrice sono presenti tutti i coefficienti delle incognite, ordinati come si come si presentano nel sistema in forma normale. Abbiamo:
\begin{bmatrix} 2 & 1 \\ 1 & 5\end{bmatrix}Osserviamo che nei termini {y} e {x} rispettivamente presenti nella prima e nella seconda equazione è sottinteso un coefficiente 1. Sentitevi liberi di riportare esplicitamente i coefficienti 1 nello scrivere i sistemi in forma normale, se questo può aiutarvi a scrivere con maggiore sicurezza la matrice dei coefficienti.
Confrontiamo in particolare il sistema di partenza con la matrice dei coefficienti:
\begin{cases} 2x+y=-10 \\ \\ x+5y=3\end{cases}; \qquad\begin{bmatrix} 2 & 1 \\ 1 & 5\end{bmatrix}Effettivamente l’ordine con il quale compaiono i coefficienti delle incognite è lo stesso dell’ordine in cui si presentano i numeri all’interno della matrice dei coefficienti. Osserviamo che i numeri o quantità letterali presenti all’interno di una matrice si chiamano più propriamente elementi.
A cosa ci serve la matrice dei coefficienti? La sua utilità sta nel poter calcolare il determinante della matrice dei coefficienti, che è un numero che ci servirà per calcolare con delle semplici formule i valori delle incognite del sistema (che qui supponiamo determinato).
Il determinante della matrice dei coefficienti si indica con {D} e si rappresenta simbolicamente come (lo scriviamo a fianco del generico sistemi lineare “due per due” al quale si riferisce):
\begin{cases} a_1x+ b_1y=k_1 \\ \\ a_2x+b_2y=k_2 \end{cases}; \qquad D = \det \begin{bmatrix} a_1 & b_1 \\ a_2 & b_2\end{bmatrix}Così nel caso del sistema che stiamo risolvendo possiamo scrivere:
D=\det \begin{bmatrix} 2 & 1 \\ 1 & 5\end{bmatrix}Ma come possiamo calcolarlo? In generale la regola è la seguente:
D = \det \begin{bmatrix} a_1 & b_1 \\ a_2 & b_2\end{bmatrix}=a_1 \cdot b_2 - a_2 \cdot b_1Per ricordarla, basta osservare che gli elementi {a_1, \: b_2} formano all’interno della matrice una diagonale discendente da sinistra verso destra, mentre gli elementi {a_2 ,\: b_1} formano all’interno della matrice una diagonale ascendente da sinistra verso destra. E infine, il determinante si ottiene come differenza tra il prodotto degli elementi della diagonale discendente, meno il prodotto degli elementi della diagonale ascendente.
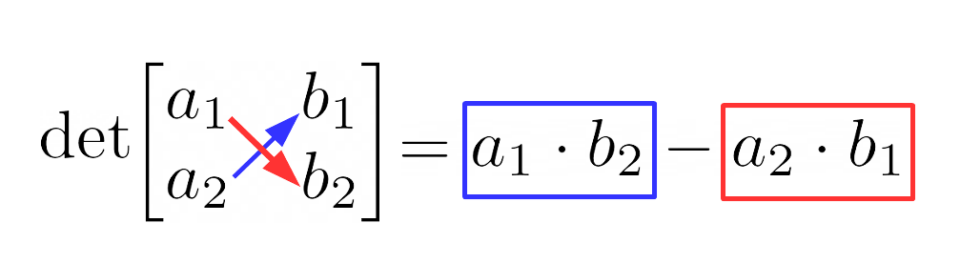
Nel nostro esempio abbiamo così:
D=\det \begin{bmatrix} 2 & 1 \\ 1 & 5 \end{bmatrix} = 2 \cdot 5 - 1 \cdot 1=10-1=9Ora, per risolvere il sistema con il metodo di Cramer, oltre al determinante della matrice dei coefficienti occorrono altri due determinanti. Il primo è il determinante della matrice che si ottiene sostituendo alla colonna dei coefficienti della {x} la colonna dei termini noti presenti nel sistema. Questo determinante si indica con {D_x} e si calcola come:
D_x=\det \begin{bmatrix} k_1 & b_1 \\ k_2 & b_2\end{bmatrix}=k_1 \cdot b_2 - k_2 \cdot b_1Come possiamo vedere si tratta solo di scrivere la matrice in modo differente, ma la regola per il calcolo del determinante è la stessa del caso precedente.
Così per il sistema in esame, che per comodità riportiamo di nuovo a seguire assieme alla matrice dei coefficienti,
\begin{cases} 2x+y=-10 \\ \\ x+5y=3\end{cases}; \qquad\begin{bmatrix} 2 & 1 \\ 1 & 5\end{bmatrix}abbiamo:
D_x = \det \begin{bmatrix} -10 & 1 \\ 3 & 5\end{bmatrix}= -10 \cdot 5 - 3 \cdot 1 = -53Come possiamo vedere, agli elementi che nella prima colonna della matrice dei coefficienti erano {2} e {1} abbiamo sostituito i termini noti del sistema, in colonna, ovvero gli elementi {-10} e {3}.
Infine, abbiamo bisogno del determinante della matrice che si ottiene sostituendo nella matrice dei coefficienti la colonna dei coefficienti dell’incognita {y} con la colonna dei termini noti del sistema. Abbiamo:
D_y = \det \begin{bmatrix} a_1 & k_1 \\ a_2 & k_2\end{bmatrix} = a_1 \cdot k_2 - a_2 \cdot k_1 ovvero nel caso in esame:
D_y = \det \begin{bmatrix}2 & -10 \\ 1 & 3 \end{bmatrix}=2 \cdot 3 - 1 \cdot (-10)=6+10=16Come evidente abbiamo sostituito agli elementi nella seconda colonna della matrice dei coefficienti i termini noti in colonna del sistema.
A questo punto per ricavare i valori delle incognite con il metodo di Cramer, noti tutti i determinanti, basta utilizzare le seguenti formule:
x=\dfrac{D_x}{D}; \qquad y=\dfrac{D_y}{D}Così abbiamo nel caso in esame:
x=\dfrac{D_x}{D}=\dfrac{-53}{9}; \qquad y=\dfrac{D_y}{D}=\dfrac{16}{9}e quindi la soluzione del sistema è in conclusione data dalla coppia ordinata di valori:
\left( -\dfrac{53}{9}, \: \dfrac{16}{9}\right)Il metodo di Cramer richiede un po’ di attenzione per il calcolo dei determinanti, ma a tal punto consente di calcolare i valori delle incognite con delle formule davvero semplici.
Tuttavia, anche tali formule pur nella loro semplicità devono essere ricordate con assoluta precisione. In particolare, ricordiamo sempre che nelle formule del metodo di Cramer il determinante {D} della matrice dei coefficienti è sempre al denominatore. 😉
Ora, come estendere il metodo al caso dei sistemi di tre equazioni in tre incognite? Beh, diciamo subito che le formule per il calcolo dei valori delle incognite sono del tutto simili a quel sin qui viste per i sistemi di due equazioni in due incognite:
x=\dfrac{D_x}{D}; \qquad y=\dfrac{D_y}{D}; \qquad z=\dfrac{D_z}{D} \qquad \text{sistemi "3
✕ 3"}Il problema è però calcolare i determinanti, che in questo caso corrispondono ai determinanti di matrici “3 per 3”, ovvero matrici con tre righe e tre colonne. Per effettuare il calcolo di determinanti di questo tipo esistono due regole: la regola di Sarrus e la regola di Laplace. In questo contesto riteniamo opportuno presentare la regola di Sarrus.
Regola di Sarrus per il calcolo dei determinanti delle matrici 3 per 3
Consideriamo la seguente matrice “3 per 3” (ovvero, in soldoni, una matrice larga 3 elementi e alta 3 elementi):
\begin{bmatrix} a & b &c \\ d &e & f \\ g & h & i\end{bmatrix}Il calcolo del suo determinante con la regola di Sarrus si effettua come segue:
\begin{align*} & \det \begin{bmatrix} a & b &c \\ d &e & f \\ g & h & i\end{bmatrix}= \\ \\ & = a \cdot e \cdot i+b \cdot f \cdot g +c \cdot d \cdot h - g \cdot e \cdot c - h \cdot f \cdot a -i \cdot d \cdot b\end{align*}Complicato ricordare la formula? Indubbiamente. Ma nessun problema. Questa può essere ricavata con una semplice regola, che somiglia già molto alla regola vista negli esempi precedenti per il calcolo del determinante di una matrice “2 per 2”. Guardiamo insieme la seguente figura:
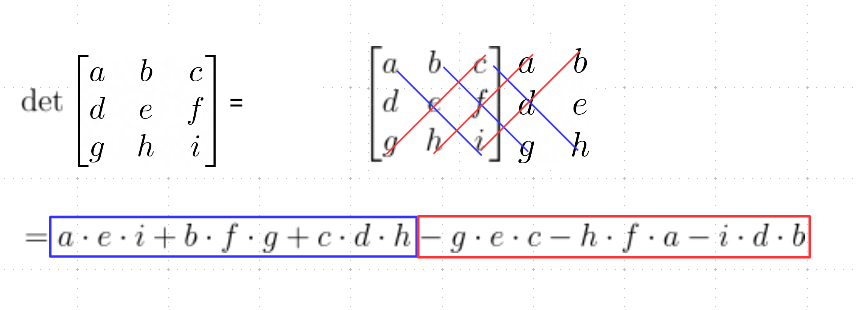
Prima di tutto abbiamo aggiunto alla matrice dei coefficienti le sue stesse prime due colonne (vedi matrice “estesa” sulla destra). A tal punto, abbiamo sommato tra loro tutti i prodotti relativi alle diagonali discendenti in blu, sottraendo poi tutti i prodotti relativi alle diagonali ascendenti in rosso.
Grazie a questa rappresentazione è più che immediato, con un po’ di allenamento, ricordare la regola di Sarrus. 😉
Vediamo allora subito come risolvere un sistema di tre equazioni in tre incognite utilizzando il metodo di Cramer.
Risolvere i sistemi di tre equazioni in tre incognite con il metodo di Cramer
Consideriamo il seguente sistema di tre equazioni in tre incognite:
\begin{cases} \dfrac{x}{2}-y+z=-1 \\ \\ 2x-\dfrac{y}{3}-\dfrac{4}{3}z=0 \\ \\ x+y-\dfrac{3}{2}z=\dfrac{1}{2}\end{cases}Il sistema è già in forma normale. Cominciamo scrivendo anzitutto la matrice dei coefficienti:
\begin{bmatrix} \frac{1}{2} & -1 & 1 \\ \\ 2 & -\frac{1}{3} & -\frac{4}{3} \\ \\ 1 & 1 & -\frac{3}{2}\end{bmatrix} \qquad \text{matrice dei coefficienti}Ora calcoliamone il determinante utilizzando la regola di Sarrus. Riportiamo per comodità, prima di eseguire i calcoli, una matrice data dalla matrice dei coefficienti nella quale ripetiamo le sue prime due colonne. Questo consentirà di individuare facilmente le diagonali discendenti e ascendenti.
La matrice dei coefficienti con le prime due colonne ripetute è:
\small \begin{bmatrix} \frac{1}{2} & -1 & 1 \\ \\ 2 & -\frac{1}{3} & -\frac{4}{3} \\ \\ 1 & 1 & -\frac{3}{2}\end{bmatrix} \:\:\begin{matrix} \frac{1}{2} & -1 \\ \\ 2 &-\frac{1}{3} \\ \\ 1 & 1\end{matrix}Per il calcolo del determinante della matrice dei coefficienti abbiamo:
\begin{align*} & D=\det \begin{bmatrix} \frac{1}{2} & -1 & 1 \\ \\ 2 & -\frac{1}{3} & -\frac{4}{3} \\ \\ 1 & 1 & -\frac{3}{2}\end{bmatrix} = \\ \\= & \scriptsize{ \dfrac{1}{2}\cdot \left(-\dfrac{1}{3} \right) \cdot \left( -\dfrac{3}{2}\right)+(-1) \cdot \left( -\dfrac{4}{3}\right)\cdot 1 +1 \cdot 2 \cdot 1 -1 \cdot \left( -\dfrac{1}{3}\right) \cdot 1 - 1 \cdot \left( -\dfrac{4}{3}\right) \cdot \dfrac{1}{2} - \left(-\dfrac{3}{2} \right) \cdot 2 \cdot (-1)=} \\ \\ & =\dfrac{1}{4}+\dfrac{4}{3}+2+\dfrac{1}{3}+\dfrac{4}{6}-3=\dfrac{3+16+24+4+8-36}{12}=\dfrac{19}{12}\end{align*}A questo punto notiamo che nel sistema in esame la colonna dei termini noti è:
\begin{matrix}-1 \\ \\ 0 \\ \\ \frac{1}{2}\end{matrix} \qquad \text{colonna termini noti}Calcoliamo il determinante {D_x}, ovvero il determinante della matrice che si ottiene sostituendo alla prima colonna della matrice dei coefficienti la colonna dei termini noti. Anzitutto la matrice che dobbiamo scrivere è:
\begin{bmatrix} -1 & -1 & 1 \\ \\ 0 & -\frac{1}{3} & -\frac{4}{3} \\ \\ \frac{1}{2} & 1 & -\frac{3}{2}\end{bmatrix}Come possiamo vedere si tratta della matrice dei coefficienti la cui terza colonna è stata sostituita con la colonna dei termini noti del sistema.
Ora ripetiamo le prime due colonne:
\small \begin{bmatrix} -1 & -1 & 1 \\ \\ 0 & -\frac{1}{3} & -\frac{4}{3} \\ \\ \frac{1}{2} & 1 & -\frac{3}{2}\end{bmatrix}\: \: \begin{matrix} -1 & -1 \\ \\ 0 & -\frac{1}{3} \\ \\ \frac{1}{2} & 1 \end{matrix}Calcoliamo il determinante della matrice:
\begin{align*} & D_x = \det \begin{bmatrix} -1 & -1 & 1 \\ \\ 0 & -\frac{1}{3} & -\frac{4}{3} \\ \\ \frac{1}{2} & 1 & -\frac{3}{2}\end{bmatrix}= \\ \\ & =-1 \cdot \left( -\dfrac{1}{3}\right) \cdot \left( -\dfrac{3}{2}\right)+(-1)\cdot\left( -\dfrac{4}{3}\right)\cdot\dfrac{1}{2}+1 \cdot 0 \cdot 1 + \\ \\ & - \dfrac{1}{2}\cdot \left( -\dfrac{1}{3}\right) \cdot 1 -1 \cdot \left( -\dfrac{4}{3}\right) \cdot (-1) - \left( -\dfrac{3}{2}\right) \cdot 0 \cdot (-1) = \\ \\ & = -\dfrac{1}{2}+\dfrac{2}{3}+0+\dfrac{1}{6}-\dfrac{4}{3}-0=-1\end{align*}Ora passiamo con una tecnica del tutto simile a {D_y}, che è il determinante della matrice dei coefficienti nella quale sostituiamo la seconda colonna dei coefficienti con la colonna dei termini noti del sistema. Abbiamo, omettendo per brevità i passaggi:
D_y = \det \begin{bmatrix} \frac{1}{2} & -1 & 1 \\ \\ 2 & 0 & -\frac{4}{3} \\ \\ 1 & \frac{1}{2} & -\frac{3}{2} \end{bmatrix}=-\dfrac{1}{3}Passiamo infine a {D_z}, che è il determinante di quella matrice che si ottiene sostituendo alla terza colonna della matrice dei coefficienti la colonna dei termini noti. Riportiamo in questo caso i calcoli completi, come ulteriore esercizio.
Ripetiamo le prime due colonne nella matrice:
\small \begin{bmatrix} \frac{1}{2} & -1 & -1 \\ \\ 2 & -\frac{1}{3} & 0 \\ \\ 1 & 1 & \frac{1}{2}\end{bmatrix} \: \:\begin{matrix} \frac{1}{2} & -1 \\ \\ 2 & -\frac{1}{3} \\ \\ 1 & 1\end{matrix}Per il calcolo del determinante abbiamo:
\begin{align*} & D_z = \det \begin{bmatrix} \frac{1}{2} & -1 & -1 \\ \\ 2 & -\frac{1}{3} & 0 \\ \\ 1 & 1 & \frac{1}{2}\end{bmatrix}= \\ \\ & = \scriptsize {\dfrac{1}{2} \cdot \left( -\dfrac{1}{3}\right) \cdot \dfrac{1}{2} + (-1) \cdot 0 \cdot 1 +(-1)\cdot2\cdot 1 - 1 \cdot \left( -\dfrac{1}{3}\right)\cdot (-1)-1 \cdot 0 \cdot \dfrac{1}{2} -\dfrac{1}{2} \cdot 2 \cdot (-1) } = \\ \\ & =-\dfrac{1}{12}+0-2-\dfrac{1}{3}-0+1= -\dfrac{17}{12}\end{align*}A questo punto non resta che calcolare i valori delle incognite, utilizzando le formule del metodo di Cramer per i sistemi di tre equazioni in tre incognite:
x=\dfrac{D_x}{D}; \qquad y=\dfrac{Dy}{D}; \qquad z=\dfrac{D_z}{z} Abbiamo, sostituendo nelle formule appena scritti i valori dei determinanti calcolati:
\small \begin{align*} & x=\dfrac{D_x}{D}=\dfrac{-1}{\dfrac{19}{12}}=-\dfrac{12}{19}; \qquad y=\dfrac{D_y}{D}=\dfrac{-\dfrac{1}{3}}{\dfrac{19}{12}}=-\dfrac{1}{3} \cdot \dfrac{12}{19}=-\dfrac{4}{19}; \\ \\ &z=\dfrac{D_z}{D}=\dfrac{-\dfrac{17}{12}}{\dfrac{19}{12}}=-\dfrac{17}{12} \cdot \dfrac{12}{19}=-\dfrac{17}{19}\end{align*}Conclusioni
Per quanto riguarda il metodo di Cramer per risolvere i sistemi lineari fino a tre equazioni in tre incognite è tutto. Ci limitiamo soltanto ad osservare, prima di salutarci, che è anche possibile calcolare i determinanti delle matrici “tre per tre” utilizzando al posto della regola di Sarrus la regola di Laplace. Quest’ultima regola consente di ricondursi al caso del calcolo di più determinanti di matrici “due per due”, ma con la difficoltà di dover stabilire di volta in volta il segno di una certa quantità in base al particolare posto occupato da un dato elemento all’interno della matrice di partenza. A nostro avviso il metodo non risulta particolarmente comodo per matrici di soli tre per tre elementi. Naturalmente, la regola di Laplace risulta praticamente inevitabile per l’utilizzo del metodo di Cramer per risolvere sistemi con più di tre equazioni, ma di questi non ci occuperemo.
Nella prossima lezione riprenderemo il metodo del confronto nel particolare caso dei sistemi di tre equazioni in tre incognite. Un saluto a tutti voi e buon proseguimento con SìMatematica!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
