In questa lezione vediamo come risolvere i sistemi lineari (sistemi di primo grado), relativamente a sistemi di equazioni contenenti due oppure tre equazioni. La trattazione è destinata agli studenti delle scuole superiori e copre tutti i metodi risolutivi. Questa lezione è dunque destinata a chi desidera effettuare uno studio intensivo. Tuttavia, sono anche disponibili lezioni dedicate a ciascun metodo risolutivo. Consigliamo comunque vivamente la lettura anche di questa lezione generale.
Un sistema lineare (o sistema di equazioni di primo grado) è l’insieme di due o più equazioni (rispettivamente in due o più incognite) entrambe di primo grado delle quali ricerchiamo le eventuali soluzioni in comune. Ad esempio, date due equazioni nelle incognite {x, \: y}, ci domandiamo se esiste una coppia {(x,y)} di valori tali da verificare entrambe le equazioni:
\begin{cases}a_1x+b_1y=k_1 \\ \\ a_2x+b_2y=k_2 \end{cases}Quello appena scritto è un sistema lineare di due equazioni in due incognite. Le incognite sono ovviamente le lettere {x} e {y}. Nelle equazioni abbiamo i coefficienti reali delle incognite {a_1}, {b_1} e {a_2}, {b_2}. Le quantità {k_1} e {k_2} sono infine dei numeri reali che rappresentano il termine noto di ciascuna equazione.
Così, se il sistema è determinato sarà possibile individuare una coppia di valori {(x,y)} tale da soddisfare entrambe le equazioni.
Nel caso in cui esistano infinite coppie tali da soddisfare entrambe le equazioni, il sistema si dirà invece indeterminato. Infine, se non esiste nessuna coppia tale da verificare entrambe le equazioni il sistema si dirà impossibile.
Precisiamo che nel corso di questa lezione ci occuperemo unicamente di sistemi determinati. Così negli esercizi che proporremo sarà sempre possibile trovare la coppia di valori {(x,y)} che verificano tutte le equazioni presenti nel sistema.
Un esempio di sistema lineare (o sistema di equazioni di primo grado) è il seguente:
\begin{cases} 3x-y=-1 \\ \\ 2x+y = 6 \end{cases}Come vedremo, il sistema è determinato ed ammette come soluzione la coppia di valori {x=1} e {y=4}. Indichiamo brevemente tale soluzione con la notazione:
(1;4)
la quale rappresenta la coppia ordinata {(x, \: y)} di valori che soddisfano entrambe le equazioni a sistema. E sottolineiamo che, trattandosi di una coppia ordinata, è fondamentale scrivere all’interno delle parentesi prima il valore della {x} e poi il valore della {y}.
Ora, è immediato convincersi che tale coppia di valori è la soluzione del sistema. Basta infatti sostituire in ciascuna equazione del sistema alla {x} il valore {1} e alla {y} il valore {4}. In tal modo entrambe le equazioni a sistema si ridurranno ad una identità (ovvero in questo caso ad uguaglianze vere del tipo numero = numero).
Prima di entrare nel vivo della lezione, diamo la definizione di sistema lineare in forma normale. E’ infatti importantissimo conoscere questa definizione per poter risolvere i sistemi lineari.
Un sistema lineare è in forma normale se in nessuna equazione abbiamo dei termini tra loro simili, se al secondo membro di ciascuna equazione abbiamo esclusivamente un valore numerico (termine noto) e inoltre se al primo membro abbiamo solo termini contenenti le incognite, con le lettere delle incognite stesse che si presentano in ordine alfabetico.
Il sistema lineare che abbiamo scritto all’inizio in forma generale:
\begin{cases}a_1x+b_1y=k_1 \\ \\ a_2x+b_2y=k_2 \end{cases}è in forma normale poiché rispetta tutti e tre i criteri dati nella definizione.
Osserviamo che prima di apprestarsi a risolvere i sistemi lineari è praticamente sempre obbligatorio ridurre prima il sistema alla forma normale (in base al metodo risolutivo utilizzato). Per fare questo basterà eseguire gli eventuali calcoli presenti in ciascuna equazione, sommare tra loro i termini simili e quindi trasportare opportunamente i termini in ciascuna equazione. Ad esempio, il seguente sistema lineare:
\begin{cases} x+3x=1+y \\ \\ 2x+5=3(2+y)\end{cases}non è in forma normale. Vediamo come ridurlo alla forma normale. Per prima cosa, calcoliamo il prodotto al secondo membro della seconda equazione:
\begin{cases} x+3x=1+y \\ \\ 2x+5=6+3y\end{cases}Ora, trasportiamo dal secondo membro al primo membro tutti i termini che contengono le incognite:
\begin{cases} x+3x-y=1 \\ \\ 2x+5-3y=6\end{cases}Proseguiamo trasportando dal primo membro al secondo membro i termini numerici (in questo caso, il solo termine {5} al primo membro della seconda equazione):
\begin{cases} x+3x-y=1 \\ \\ 2x-3y=6-5\end{cases}Infine sommiamo i termini simili in ciascuna equazione:
\begin{cases} 4x-y=1 \\ \\ 2x-3y=1\end{cases}Il sistema è ora in forma normale. 😉
Fatte le dovute premesse, vediamo subito come risolvere i sistemi lineari (sistemi di equazioni di primo grado), studiando un metodo alla volta. Per ciascun metodo proporremo prima la risoluzione di sistemi lineari con due equazioni e due incognite, per poi passare ai sistemi lineari con tre equazioni e tre incognite. Via! 🙂
Metodo di sostituzione (risolvere i sistemi lineari, o sistemi di primo grado)
Il metodo più semplice per risolvere i sistemi lineari è il metodo di sostituzione. Questa tecnica risolutiva è abbastanza agevole per i sistemi di due equazioni in due incognite, mentre diventa un po’ lenta ed inefficiente per sistemi dalle tre equazioni in poi. Da ciò la necessità di saper utilizzare anche gli altri metodi che vedremo a seguire.
Riprendiamo uno dei due sistemi lineari di due equazioni in due incognite scritti in precedenza:
\begin{cases} 3x-y=-1 \\ \\ 2x+y = 6 \end{cases}Osserviamo anzitutto che il sistema è già in forma normale e quindi possiamo iniziare sin d’ora a risolverlo senza alcuna preparazione.
Ora, come è evidente non è possibile risolvere ciascuna equazione singolarmente. Infatti, le incognite sono due. E quindi al massimo ciò che potremmo fare è ricavare un’incognita in funzione dell’altra. Ad esempio, ricavando la {x} dalla prima equazione:
\begin{cases} 3x=y-1 \quad \Rightarrow \quad x = \dfrac{y-1}{3} \\ \\2x+y=6\end{cases} Possiamo quindi riscrivere il sistema come:
\begin{cases} x = \dfrac{y-1}{3} \\ \\2x+y=6\end{cases}Tuttavia, il problema è dato dal fatto che per la {x} non siamo riusciti a ricavare un valore numerico ma piuttosto un’espressione nell’altra incognita {y}.
Ma a questo punto cerchiamo di utilizzare ciò che già sappiamo fare: ricavare la eventuale soluzione di un’equazione di primo grado. Così, per risolvere il sistema l’idea è quella di riscrivere le equazioni in esso presenti di modo che contengano una sola incognita. In tal modo, sarà possibile ricavare un valore numerico per le incognite.
Ora, vediamo di utilizzare l’espressione precedentemente ricavata per {x} dalla prima equazione:
{\dfrac{y-1}{3}}In particolare, l’idea è quella di sostituire tale espressione nella seconda equazione del sistema, al posto della lettera x:
\begin{cases} x=\dfrac{y-1}{3} \\ \\ 2x+y = 6 \quad \text{con} \quad x=\dfrac{y-1}{3} \quad \Rightarrow \quad \boxed{2\left( \dfrac{y-1}{3}\right)+y=6} \end{cases} In altre parole, abbiamo preso la seconda equazione del sistema ed abbiamo sostituito alla {x} l’espressione {\dfrac{y-1}{3}}. Così facendo, sviluppando i calcoli nell’equazione racchiusa nel riquadro otteniamo un’equazione di primo grado in una sola incognita (seconda equazione nel sistema):
\begin{cases} x=\dfrac{y-1}{3} \\ \\ \dfrac{2y-2+3y-18}{3}=0\end{cases} dalla quale ricaviamo facilmente il valore dell’incognita {y}:
\begin{cases} x=\dfrac{y-1}{3} \\ \\ \dfrac{2y-2+3y-18}{3}=0 \quad \rightarrow \quad \dfrac{5y-20}{\cancel{3}}=0 \quad \rightarrow \quad \boxed{y=4}\end{cases} Così il sistema diviene:
\begin{cases} x=\dfrac{y-1}{3} \\ \\ {y=4}\end{cases} Finalmente siamo riusciti a ricavare per una delle due incognite un valore numerico.
A questo punto, per ricavare il valore dell’incognita {x} non ci resta che sostituire il valore appena ricavato per l’incognita y nella prima equazione del sistema. In altre parole, basterà sostituire alla lettera {y} nella prima equazione il valore {4}. In tal modo, la prima equazione diventa un’equazione di primo grado in una sola incognita (x). Otteniamo:
\begin{cases} x=\dfrac{y-1}{3} \quad \rightarrow \quad x=\dfrac{4-1}{3}=\dfrac{3}{3}=1 \quad \rightarrow \quad \boxed{x=1} \\ \\ y=4\end{cases}In questo modo abbiamo trovato un valore numerico anche per la rimanente incognita {x}.
A questo punto abbiamo dei valori numerici per entrambe le incognite, in particolare:
x=1, \qquad y=4
Di conseguenza il sistema è determinato ed ha per soluzione la coppia ordinata {(x, \: y)} di valori:
(1; 4)
Abbiamo così già visto il nostro primo esempio pratico su come risolvere i sistemi lineari. 🙂
Possiamo a questo punto riassumere il metodo di sostituzione per i sistemi lineari (o di primo grado) con due equazioni in due incognite come segue:
- ricavare un’espressione di un’incognita in funzione dell’altra incognita da una delle due equazioni;
- sostituire l’espressione appena ricavata nell’altra equazione, ottenendo un’equazione di primo grado in una sola incognita;
- risolvere l’equazione appena ottenuta ricavando un valore numerico per un’incognita;
- sostituire il valore numerico appena ottenuto nella rimanente equazione del sistema, ottenendo un’altra equazione di primo grado in una sola incognita;
- risolvere l’equazione di primo grado appena scritta ottenendo in conclusione il valore numerico per l’incognita rimanente.
Vediamo un ulteriore esempio su come risolvere i sistemi lineari di due equazioni in due incognite utilizzando il metodo di sostituzione:
\begin{cases}2x-y=1 \\ \\ 3x - 2y = -1 \end{cases}Anche in questo caso il sistema è in forma normale e possiamo quindi cominciare direttamente a risolverlo. Precisiamo che per applicare il metodo di sostituzione non è strettamente necessario per la verità che il sistema sia in forma normale, ma è comunque obbligatorio che non vi siano termini simili in nessuna equazione. 😉
Ora, risolviamo il sistema.
Possiamo partire indifferentemente dalla prima o dalla seconda equazione. Appare più comodo ricavare ad esempio la {y} dalla prima equazione:
\begin{cases}-y=1-2x \quad \Rightarrow \quad y=2x-1 \\ \\ 3x-2y=-1 \end{cases}Ora sostituiamo l’espressione ottenuta per l’incognita {y} nella seconda equazione.
\small \begin{cases}y=2x-1\\ \\ 3x - 2y = -1 \quad \text{con} \quad y=2x-1 \quad \Rightarrow \quad 3x-2\left( 2x-1\right)+1=0\end{cases}da cui svolgendo i calcoli ricaviamo:
\begin{cases}y=2x-1 \\ \\ 3x-4x+2+1=0 \quad \rightarrow \quad -x=-3 \quad \rightarrow \quad \boxed{x=3} \end{cases}Adesso lavoriamo con la prima equazione, sostituendo alla {x} il valore appena trovato per essa, ovvero {3}:
\begin{cases}y=2x-1 \quad \rightarrow \quad y=2 \cdot 3 - 1 \quad \rightarrow \quad \boxed{y=5} \\ \\ x=3\end{cases}Così il sistema è determinato ed ammette come soluzione la coppia ordinata {(x,y)}:
(3;5)
Metodo di sostituzione per sistemi lineari con tre equazioni in tre incognite
Vediamo ora di estendere il metodo appena imparato per risolvere i sistemi lineari (o sistemi di primo grado) aventi tre equazioni in tre incognite. Tali sistemi si presentano nella forma normale:
\begin{cases} a_1x+b_1y+c_1z=k_1 \\ \\ a_2x+b_2y+c_2z=k_2 \\ \\ a_3x+b_3y+c_3z=k_3\end{cases}ove {a_i, \: b_i, \: c_i} (con {i=1, 2, 3}) sono i coefficienti reali delle incognite di ciascuna equazione, mentre {k_1, \: k_2, \: k_3} sono i rispettivi termini noti.
In parole povere si tratta di sistemi lineari aventi tre equazioni tutte di primo grado, ciascuna avente generalmente le incognite {x, \: y, \: z}.
Se il sistema è determinato, esso avrà per soluzione una terna ordinata di valori {(x,\: y, \: z)}. Ancora, trattandosi di una terna ordinata è fondamentale inserire i valori delle incognite all’interno delle parentesi nell’ordine indicato.
Avendo tre equazioni, l’applicazione del metodo di sostituzione potrebbe apparire difficile a prima vista. Tuttavia, la chiave sta nel considerare all’inizio soltanto due equazioni, mettendo da parte la terza equazione ed utilizzandola solo alla fine. Tenendo conto di questa regola sarà possibile risolvere agevolmente i sistemi lineari di tre equazioni in tre incognite con il metodo di sostituzione, senza incorrere nel rischio di rimanere intrappolati in un vicolo cieco.
Consideriamo ad esempio il sistema:
\begin{cases} x-2y-7=0 \\ \\ 2x+3y=0 \\ \\ x-y+2z=5\end{cases}Osserviamo che nella prima e nella seconda equazione manca un’incognita. In realtà questa è comunque presente ma con coefficiente zero. Ciò quindi non invalida la definizione di sistema lineare di tre equazioni in tre incognite. Infatti complessivamente abbiamo comunque tre incognite nel sistema.
Scegliamo le due equazioni con le quali iniziare a lavorare. Ha sicuramente senso prendere le prime due equazioni, dato che entrambe presentano un numero ridotto di incognite. Ci ritroviamo così a risolvere per il momento un sistema praticamente di due equazioni in due incognite:
\begin{cases} x-2y-7=0 \\ \\ 2x+3y=0 \\ \\ \dots\end{cases}Abbiamo sostituito la terza equazione con dei puntini, come a dire: per ora l’abbiamo tolta, ma poi ricordiamoci di lei!
Ricavando la {x} e la {y} dalle due equazioni considerate, utilizzando né più né meno che il metodo di sostituzione per i sistemi di due equazioni in due incognite, otteniamo:
\small \begin{cases}x = 2y+7 \\ \\ 2(2y+7)+3y=0 \\ \\ \dots \end{cases} \quad \begin{cases} x=2y+7 \\ \\ 4y+14+3y=0 \\ \\ \dots \end{cases} \quad \begin{cases}x=2y+7 \\ \\y=-2 \\ \\ \dots \end{cases}e sostituendo il valore ricavato per {y} nella prima equazione:
\begin{cases}x=3 \\ \\ y=-2 \\ \\ \dots\end{cases}A questo punto dobbiamo ricavare l’incognita {z}. Ma per fare ciò basta far riapparire l’equazione che avevamo lasciato da parte, scrivendola al posto dei puntini:
\begin{cases}x=3 \\ \\ y=-2 \\ \\ x-y+2z=5 \end{cases}Per ricavare la {z} basta a questo punto sostituire alle lettere {x} e {y} nella terza equazione i valori rispettivamente {3} e {-2}:
\begin{cases}x=3 \\ \\ y=-2 \\ \\ 3-(-2)+2z=5 \quad \Rightarrow \quad z=\dfrac{5-3-2}{2}=0 \end{cases}Così in conclusione il sistema è determinato ed ha per soluzione la terna di valori
(3; -2; 0)
nella quale indichiamo ordinatamente i valori per le incognite {x, \: y, \: z} che soddisfano contemporaneamente le tre equazioni del sistema.
Vediamo ora un ulteriore esempio nel quale compaiono esplicitamente tutte e tre le incognite in ciascuna equazione. Risolviamo il sistema lineare in tre equazioni e tre incognite:
\begin{cases}x-3y-z = 1 \\ \\ 3x+3y+z=6 \\ \\ x-y-2z=-1 \end{cases}Come fatto in precedenza, potremmo eliminare un’equazione ragionando per il momento soltanto con le rimanenti due. Ad esempio:
\begin{cases}x-3y-z = 1 \\ \\ \dots \\ \\ x-y-2z=-1 \end{cases}Tuttavia, come possiamo vedere in questo caso abbiamo un problema: ci ritroviamo con due equazioni in tre incognite. Ed avendo tre incognite ci manca un’equazione.
Quindi, in generale, prima di eliminare un’equazione dobbiamo ricavare grazie ad essa l’espressione di un’incognita in funzione delle altre due. Nell’esercizio precedente ciò non è stato necessario poiché in due equazioni comparivano esplicitamente soltanto due incognite. Ma ora ci ritroviamo nel caso più generale.
Quindi, torniamo indietro al sistema di partenza:
\begin{cases}x-3y-z = 1 \\ \\ 3x+3y+z=6 \\ \\ x-y-2z=-1 \end{cases}Consideriamo ad esempio la seconda equazione e ricaviamo da essa un’espressione per l’incognita {z} in funzione delle altre incognite:
\begin{cases}x-3y-z = 1 \\ \\ 3x+3y+z=6 \quad \rightarrow \quad z = 6-3x-3y \\ \\ x-y-2z=-1 \end{cases}Così il sistema diviene:
\begin{cases}x-3y-z = 1 \\ \\ z =\boxed{{ 6-3x-3y}} \\ \\ x-y-2z=-1 \end{cases} Poiché vogliamo ricondurci ad un sistema di due equazioni in due sole incognite, l’idea è chiaramente quella di sostituire la {z} nella prima e nella terza equazione con l’espressione evidenziata nel riquadro. Abbiamo in questo modo:
\begin{cases}x-3y-(\boxed{6-3x-3y}) = 1 \\ \\ z ={ \boxed{6-3x-3y}} \\ \\ x-y-2(\boxed{6-3x-3y})=-1 \end{cases} Osserviamo che ora nella prima e nella terza equazione abbiamo le sole incognite {x} e {y}. Conviene allora mettere da parte la seconda equazione, che sostituiamo con dei puntini. In questo modo riusciamo a ricondurci temporaneamente ad un sistema di due sole equazioni in due incognite.
\begin{cases}x-3y-(6-3x-3y) = 1 \\ \\ \dots \\ \\ x-y-2(6-3x-3y)=-1 \end{cases} Così, cominciando a sviluppare i calcoli al primo membro di ciascuna equazione:
\begin{cases}x-3y-6+3x+3y = 1 \\ \\ \dots \\ \\ x-y-12+6x+6y=-1 \end{cases}ossia:
\begin{cases}4x=7 \\ \\ \dots \\ \\ 7x+5y=11 \end{cases}da cui, ragionando come in un sistema di due equazioni in due incognite, ricaviamo agevolmente:
\begin{cases}x=\dfrac{7}{4} \\ \\ \dots \\ \\ 7 \cdot \dfrac{7}{4}+5y=11 \quad \Rightarrow \quad \end{cases} \begin{cases}x=\dfrac{7}{4} \\ \\ \dots \\ \\ y=-\dfrac{1}{4} \end{cases}A questo punto per ricavare la {z} non resta che recuperare la seconda equazione che avevamo messo da parte, riscrivendola al posto dei puntini:
\begin{cases}x=\dfrac{7}{4} \\ \\ z=6-3x-3y\\ \\ y=-\dfrac{1}{4} \end{cases}Sostituendo nella seconda equazione i valori della {x} e della {y} ricavati otteniamo:
\begin{cases}x=\dfrac{7}{4} \\ \\ z=6-3 \cdot \dfrac{7}{4}-3\cdot \left( -\dfrac{1}{4}\right)=6-\dfrac{21}{4}+\dfrac{3}{4}=\dfrac{3}{2}\\ \\ y=-\dfrac{1}{4} \end{cases}Abbiamo quindi ricavato i valori di tutte e tre le incognite ed in conclusione la soluzione del sistema è data dalla terna:
\left( \dfrac{7}{4}; -\dfrac{1}{4}; \dfrac{3}{2}\right)NOTA. Per ulteriori dettagli sul metodo di sostituzione: metodo di sostituzione per i sistemi lineari.
Metodo di riduzione (per sistemi lineari o di primo grado)
Introduciamo ora il metodo di riduzione per risolvere i sistemi lineari. Il metodo risulta particolarmente utile per i sistemi dalle tre equazioni in su, in quanto meno macchinoso rispetto al metodo per sostituzione.
Come per il metodo per sostituzione, cominciamo ad introdurre il metodo di riduzione partendo dal caso di un sistema avente due equazioni in due incognite. Supporremo anche in questa circostanza di avere a che fare con sistemi determinati.
Il metodo di riduzione si basa sui principi di equivalenza delle equazioni, e ne rappresenta una rilettura per il caso dei sistemi lineari. Consideriamo le due equazioni:
A=B; \qquad C=D
Proviamo ad applicare il primo principio di equivalenza alla prima equazione. Considerando una quantità {Q} che rispetta le ipotesi date a suo tempo per il primo principio di equivalenza, abbiamo:
A=B \iff A+Q=B+Q
In altre parole l’equazione {A+Q=B+Q} è equivalente all’equazione {A=B}.
Ora, poiché la seconda delle equazioni di partenza afferma che le quantità {C} e {D} sono uguali tra loro, possiamo indifferentemente utilizzare al posto di {Q} la quantità {C} oppure la quantità {D}, ed ha quindi perfettamente senso scrivere:
A=B \iff A+C=B+D
Ma è immediato osservare che l’equazione {A+C=B+D} si ottiene sommando membro a membro le due equazioni {A=B} e {C=D}. In altre parole dobbiamo scrivere un’equazione che abbia al primo membro la somma dei primi membri delle due equazioni, e al secondo membro la somma dei secondi membri delle due stesse equazioni:
\underline{A}=\underline{\underline{B}}, \quad \underline{C}=\underline{\underline{D}} \quad \Rightarrow \quad \boxed{\underline{A}+\underline{C}=\underline{\underline{B}}+\underline{\underline{D}}}A questo punto è fondamentale osservare che l’equazione racchiusa nel riquadro è equivalente ad entrambe le equazioni di partenza. E ciò ovviamente perché abbiamo applicato correttamente il primo principio di equivalenza.
Ora, consideriamo il seguente sistema di due equazioni in due incognite:
\begin{cases} 2x-y-10=0 \\ \\ y-5= x\end{cases}Utilizzando il ragionamento appena fatto, l’idea è quella di sostituire una delle due equazioni con un’altra ad esse equivalente. E vogliamo ricavare tale equazione equivalente a quelle date proprio sommando le due equazioni membro a membro. Ma la cosa va fatta in maniera furba e corretta. 😉
Anzitutto, dobbiamo ricondurre il sistema alla forma normale. Dobbiamo cioè riscriverlo come:
\begin{cases}a_1x+b_1y=k_1 \\ \\ a_2x+b_2y=k_2 \end{cases}Si tratterà quindi di trasportare opportunamente i termini in ciascuna equazione del sistema da risolvere. Nel nostro caso abbiamo:
\begin{cases}2x-y=10 \\ \\ -x + y=5 \end{cases}In questo modo figurano al secondo membro di ciascuna equazione soltanto dei numeri, e ai primi membri abbiamo soltanto termini non noti e tra loro non simili tutti contenenti le incognite {x} e {y}. Inoltre, in ciascuna equazione le incognite si presentano in ordine alfabetico.
Ma a questo punto quale è l’astuzia da adottare? Ciò che dobbiamo fare è sommare membro a membro le equazioni date tra loro, in modo da ottenere una terza equazione che contenga un’incognita in meno rispetto alle equazioni di partenza. In altre parole dobbiamo scrivere un’equazione che abbia un numero ridotto di incognite, da cui il nome di metodo di riduzione.
Osservando che al primo membro della prima equazione abbiamo il termine {-y}, mentre al primo membro della prima equazione abbiamo il termine {y}, è chiaro che sommando tra di loro i primi membri delle due equazioni l’incognita {y} sparirà (il sistema è in forma normale). Così sommando membro a membro le due equazioni tra loro otteniamo una terza equazione nella sola incognita {x}:
2x-y+(-x+y)=10+5 \quad \Rightarrow \quad x=15
In questo particolare caso abbiamo già ricavato il valore della prima incognita. Comunque, consideriamo l’equazione ottenuta {x=15}, e sostituiamola ad una delle due equazioni presenti nel sistema.
Sostituendola ad esempio alla prima equazione del sistema otteniamo:
\begin{cases}x=15 \\ \\ -x + y=5 \end{cases}A questo punto è evidente che possiamo procedere sostituendo il valore della {x} nella seconda equazione. Tuttavia, come ulteriore allenamento procediamo ancora utilizzando il metodo di riduzione.
Dato che la seconda equazione presenta due incognite, il nostro obiettivo è fare in modo che la seconda equazione del sistema presenti la sola incognita {y}. In tal modo, sarà possibile ricavare il valore della {y}. Per fare questo, ricaviamo una nuova equazione sommando membro a membro le due equazioni attualmente presenti nel sistema tra loro:
x+(-x+y)=15+5 \quad \rightarrow \quad y=20
Abbiamo così ottenuto grazie al metodo di riduzione anche il valore dell’incognita {y}. Così in conclusione i valori delle incognite sono:
x=15, \quad y=20
e quindi il sistema dato ha per soluzione la coppia di valori:
(15; 20)
Il metodo appena visto può apparire inutilmente complicato per il caso di sistemi con sole due equazioni. Tuttavia, esso consente di risolvere più agevolmente i sistemi con tre equazioni in tre incognite rispetto al metodo di sostituzione, come vedremo tra un istante.
Metodo di riduzione per sistemi lineari con tre equazioni in tre incognite
Vediamo come applicare il metodo di riduzione al caso dei sistemi lineari (o di primo grado) contenenti tre equazioni in tre incognite. Risolviamo il seguente sistema:
\begin{cases} x+z+y= 6 \\ \\ x-z-1=0 \\ \\ 2x+5y-3z=5\end{cases}Riscriviamo il sistema in forma normale. In questo caso basta soltanto riordinare dei termini al primo membro della prima equazione e trasportare al secondo membro il termine noto nella seconda equazione:
\begin{cases}x+y+z= 6 \\ \\ x-z=1 \\ \\ 2x + 5y-3z = 5 \end{cases}Facciamo caso che sommando membro a membro le prime due equazioni scompare l’incognita {z}:
x+y+z+(x-z)=6+1 \quad \Rightarrow \quad \boxed{2x+y=7}Abbiamo così ottenuto un’equazione equivalente a ciascuna delle equazioni utilizzate per ricavarla e che presenta il vantaggio di avere un numero di incognite ridotto. Se dunque sostituiamo l’equazione appena ottenuta ad una delle due equazioni utilizzate per ricavarla ci ritroveremo con un sistema equivalente a quello di partenza ma più facile da risolvere.
Ora, attenzione. Poiché abbiamo lavorato con le prime due equazioni, possiamo sostituire soltanto una di tali equazioni con la nuova equazione appena ottenuta. Diversamente, ci ritroveremmo in un vicolo cieco e non riusciremmo a risolvere il sistema. Quindi, stiamo attenti a non lavorare sulla rimanente equazione.
Sostituiamo ad esempio la prima equazione con la nuova equazione ottenuta:
\begin{cases}2x+y=7 \\ \\ x-z=1 \\ \\ 2x + 5y-3z = 5 \end{cases}Ora la prima equazione nel sistema è in due sole incognite, e non più tre. Anche la seconda equazione presenta due sole incognite, ma queste sono differenti. Tuttavia, vorremmo avere nella prima equazione le stesse incognite della seconda equazione. In tal modo sarebbe possibile ricondursi temporaneamente ad un sistema di due sole equazioni in due incognite.
Supponiamo ad esempio di voler lasciare la prima equazione. Dalla seconda e dalla terza equazione dobbiamo allora ricavare una nuova equazione ad esse equivalenti ma tale da contenere le sole due incognite {x} e {y}. Dobbiamo quindi eliminare l’incognita {z}.
Cominciamo allora moltiplicando la seconda equazione per {-3}. Pensiamo a questo valore poiché nella terza equazione abbiamo un termine {-3z}, mentre nella seconda equazione abbiamo un termine {-z}.
\begin{cases}2x+y=7 \\ \\ -3(x-z)=-3 \cdot 1 \\ \\ 2x + 5y-3z = 5 \end{cases} \quad \Rightarrow \quad \begin{cases}2x+y=7 \\ \\ -3x+3z=-3 \\ \\ 2x+5y-3z=5 \end{cases}Ora scriviamo una nuova equazione sommando tra loro la seconda e la terza equazione, membro a membro:
-3x+3z+2x+5y-3z=-3+5 \quad \Rightarrow \quad \boxed{-x+5y=2}Come possiamo vedere i termini {3z} e {-3z} si cancellano tra loro ed otteniamo un’equazione nelle sole due incognite {x} e {y}.
Ora, attenzione. Abbiamo lavorato con la seconda e la terza equazione, quindi possiamo sostituire la nuova equazione scritta soltanto ad una di esse. Sostituiamola ad esempio alla terza equazione, che è quella che contiene più incognite. Abbiamo:
\begin{cases}2x+y=7 \\ \\ -3x+3z=-3 \\ \\ -x+5y=2 \end{cases}Adesso è fondamentale osservare che la prima e la terza equazione sono nelle due stesse incognite x e y. Di conseguenza, dobbiamo a questo punto mettere da parte la seconda equazione e ragionare soltanto con la prima e la terza equazione. In tal modo ci ritroviamo per il momento con un sistema di due equazioni in due incognite:
\begin{cases}2x+y=7 \\ \\\dots \\ \\ -x+5y=2 \end{cases}Per semplicità ricaviamo i valori delle incognite {x} e {y} utilizzando il metodo di sostituzione. Dalla prima equazione abbiamo:
\begin{cases}2x+y=7 \quad \rightarrow \quad y=7-2x\\ \\\dots \\ \\ -x+5y=2 \end{cases}Sostituendo nella terza equazione:
\small \begin{cases}y=7-2x\\ \\\dots \\ \\ -x+5(7-2x)=2 \quad \rightarrow \quad -x+35-10x=2 \quad \rightarrow \quad x=3 \end{cases}A questo punto sostituendo il valore appena trovato per la {x} nella prima equazione abbiamo:
\small \begin{cases}y=7-2x \quad \rightarrow y=7-2\cdot3 \quad \rightarrow \quad y=1\\ \\\dots \\ \\x=3\end{cases}Ci rimane ora da ricavare il valore dell’incognita {z}. Ma come sappiamo per fare questo basta riprendere la seconda equazione, sostituendo in essa i valori noti delle incognite (in questo particolare caso, basta sostituire il solo valore dell’incognita {x}). Abbiamo:
\small \begin{cases} y=1\\ \\ -3x+3z=-3 \quad \rightarrow \:z=\dfrac{-3+3x}{3}=\dfrac{-3+3\cdot3}{3} \quad \rightarrow \: z=2 \\ \\x=3\end{cases}In conclusione il sistema è determinato ed è risolto per i valori delle incognite:
x=3, \quad y=1, \quad z=2
Ovvero, il sistema ha per soluzione la terna:
(3; 1; 2)
Vediamo un ulteriore esempio, sempre relativo al metodo di riduzione applicato ad un sistema di tre equazioni in tre incognite. Risolviamo il seguente sistema:
\begin{cases}x-3y-z=1 \\ \\ 3x+3y-z=6 \\ \\ x-y-2z=-1 \end{cases}Il sistema si presenta già in forma normale. L’idea è quella di applicare il metodo di riduzione due volte, in modo da sostituire due equazioni del sistema con due nuove equazioni contenenti due incognite anziché tre. Fatto questo, mettendo la rimanente equazione da parte ci ritroveremo con un sistema di due equazioni in due incognite, risolvendo il quale otterremo i valori di due incognite. Riprendendo l’equazione messa da parte sarà infine possibile ricavare il valore della rimanente incognita.
Cominciamo sommando algebricamente le prime due equazioni a sistema. Queste infatti contengono i termini rispettivamente {-3y} e {3y}, i quali se sommati tra loro si cancellano. In tal modo eliminiamo l’incognita {y}, ottenendo un’equazione nelle sole incognite {x} e {z}:
x-3y-z+3x+3y-z=1+6 \quad \Rightarrow \quad \boxed{4x-2z=7}Ora attenzione: abbiamo lavorato con la prima e la seconda equazione. Di conseguenza, possiamo sostituire la nuova equazione ottenuta soltanto ad una di queste due. Sostituendola ad esempio alla seconda abbiamo:
\begin{cases}x-3y-z=1 \\ \\ 4x-2z=7 \\ \\ x-y-2z=-1 \end{cases}Ora la seconda equazione ha due sole incognite (la {x} e la {z}), ma le altre equazioni ne hanno ancora tre. Dobbiamo quindi applicare di nuovo il metodo di riduzione, ad esempio tra la prima e la terza equazione. In particolare, moltiplicando entrambi i membri della terza equazione per {-3} e quindi sommando la prima e la terza equazione membro a membro, riusciamo ad ottenere una nuova equazione nelle sole incognite {x} e {z}. Abbiamo:
\begin{cases}x-3y-z=1 \\ \\ 4x-2z=7 \\ \\ \underbrace{-3x+3y+6z=3}_{\text{entrambi i membri } \times -3} \end{cases}Somma membro a membro della prima e della terza equazione:
x-\cancel{3y}-z-3x+\cancel{3y}+6z=1+3 \quad \Rightarrow \quad \boxed{-2x+5z=4}Ora, possiamo sostituire l’equazione evidenziata soltanto alla prima o alla terza equazione a sistema. Sostituendola ad esempio alla terza abbiamo:
\begin{cases}x-3y-z=1 \\ \\ 4x-2z=7 \\ \\ -2x+5z=4 \end{cases}Ora, la seconda e la terza equazione sono entrambe nelle due sole incognite {x} e {z}. Di conseguenza, mettendo da parte la prima equazione ci ritroviamo con un sistema di due equazioni in due incognite:
\begin{cases} \dots \\ \\ 4x-2z=7 \\ \\ -2x+5z=4 \end{cases}Procediamo per comodità per sostituzione. Ricaviamo ad esempio la {z} dalla seconda equazione:
\begin{cases} \dots \\ \\ 4x-2z=7 \quad \rightarrow \quad z=\dfrac{4x-7}{2}\\ \\ -2x+5z=4 \end{cases}Sostituiamo l’espressione ottenuta alla lettera {z} nella terza equazione:
\small \begin{cases} \dots \\ \\ z=\dfrac{4x-7}{2}\\ \\ -2x +5 \left( \dfrac{4x-7}{2}\right)=4 \quad \Rightarrow \quad -2x=4-10x+\dfrac{35}{2} \: \rightarrow \: x= \dfrac{43}{16} \end{cases}Ora sostituiamo il valore della {x} appena ottenuto nella seconda equazione:
\begin{cases} \dots \\ \\ z=\dfrac{4x-7}{2}\quad \rightarrow \:z=\dfrac{4\cdot\dfrac{43}{16}-7}{2}\quad \rightarrow \: z=\dfrac{15}{8} \\ \\ x=\dfrac{43}{16}\end{cases}Infine non resta che recuperare l’equazione che avevamo messo in precedenza da parte, in modo da ricavare il valore della {y}:
\begin{cases} x-3y-z=1 \\ \\ z=\dfrac{15}{8} \\ \\ x=\dfrac{43}{16}\end{cases}e quindi:
\small \begin{cases} \dfrac{43}{16}-3y-\dfrac{15}{8}=1 \quad \Rightarrow \quad -3y=1-\dfrac{43}{16}+\dfrac{15}{8} \quad \Rightarrow \quad y=-\dfrac{1}{16} \\ \\ z=\dfrac{15}{8} \\ \\ x=\dfrac{43}{16}\end{cases}In conclusione il sistema ha per soluzione la terna:
\left( \dfrac{43}{16}; -\dfrac{1}{16}; \dfrac{15}{8}\right)Uno stretto parente del metodo di riduzione è il metodo del confronto, al quale dedicheremo la prossima lezione. Tralasciamo per il momento tale metodo poiché effettivamente è solo una variante del metodo di riduzione, che tra l’altro si applica convenientemente solo in casi non molto frequenti. Proseguiamo invece la lezione occupandoci della regola di Cramer (o metodo di Cramer).
NOTA. Per ulteriori dettagli sul metodo di riduzione: metodo di riduzione per i sistemi lineari.
Regola di Cramer (o metodo di Cramer)
Il metodo di Cramer per i sistemi lineari è un metodo che consente di risolvere i sistemi lineari in modo piuttosto meccanico. Tra l’altro, a differenza degli altri metodi la regola di Cramer non è significativamente più complicata da applicare nel caso dei sistemi di tre equazioni in tre incognite rispetto al caso dei sistemi di due equazioni in due incognite.
Due aspetti sono di particolare importanza per poter risolvere i sistemi lineari applicando correttamente la regola di Cramer:
- il sistema deve essere tassativamente in forma normale. Eventualmente sarà nostra cura trasportare opportunamente i termini in ciascuna equazione in modo da ricondurre il sistema di partenza alla forma normale;
- occorre aver presenti le definizioni di determinante di una matrice due per due e di determinante di una matrice tre per tre.
In merito al primo punto, abbiamo già chiarito in precedenza che un sistema ad esempio di due equazioni e due incognite in forma normale appare come:
\begin{cases} a_1x+b_1y=k_1 \\ \\ a_2x+b_2y=k_2\end{cases}Osserviamo ancora che al primo membro di ciascuna equazione sono presenti soltanto monomi tra loro non simili aventi parti letterali {x} e {y}. Al secondo membro sono invece presenti esclusivamente dei termini noti (numeri reali).
Inoltre, le parti letterali dei monomi al primo membro di ciascuna equazione sono ordinate secondo l’alfabeto. In altre parole, al primo membro le incognite devono susseguirsi secondo l’ordine dell’alfabeto.
Attenzione: è possibile applicare la regola di Cramer (o metodo di Cramer) soltanto dopo aver ridotto il sistema da risolvere alla forma normale.
Premettiamo alcune definizioni fondamentali per poter risolvere i sistemi lineari con la regola di Cramer.
Matrici e determinanti (definizioni non rigorose)
Proponiamo ora delle definizioni intuitive dei concetti di matrice e determinante di una matrice, che risulteranno comunque utili per risolvere i sistemi con la regola o metodo di Cramer. Ci proporremo in ogni caso di fornire delle definizioni più rigorose nelle lezioni successive.
Una matrice è un particolare oggetto matematico formato da righe e colonne, simile ad una tabella, che contiene dei numeri (nel nostro caso reali). Una matrice {2 \times 2} è una matrice costituita da due righe e due colonne:
\begin{bmatrix}
a & b \\ c & d
\end{bmatrix}Nella prima riga abbiamo le quantità {a} e {b}, mentre nella seconda riga abbiamo le quantità {c} e {d}. Le colonne sono invece individuate in senso verticale. Nella prima colonna abbiamo le quantità {a} e {c}, mentre nella seconda colonna abbiamo le quantità {b} e {d}.
Una matrice {3 \times 3}, allo stesso modo, sarà del tipo:
\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}E’ possibile rappresentare ciascuna matrice con una lettera maiuscola dell’alfabeto. Così ad esempio se vogliamo rappresentare la prima matrice con la lettera {A} scriveremo:
A=\begin{bmatrix} a & b \\ c & d \end{bmatrix}Il determinante della matrice appena scritta, che si indica con {\det A}, è una particolare quantità numerica che si calcola come segue:
\det A = \det \begin{bmatrix} a & b \\ c & d \end{bmatrix} = a \cdot d - c \cdot bPer ricordare meglio la formula, basta osservare che i numeri contenuti in ciascun prodotto individuano all’interno della matrice una rispettiva diagonale:
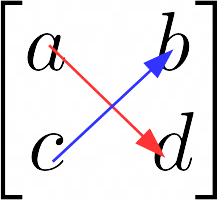
Così ad esempio i numeri {a} e {d} individuano una diagonale (discendente da sinistra verso destra, in rosso), mentre i numeri {c} e {b} individuano un’altra diagonale (ascendente da sinistra verso destra, in blu).
La diagonale in rosso è detta “diagonale principale” mentre la diagonale in blu è detta “diagonale secondaria”.
Così, per il calcolo del determinante di una matrice di due righe e due colonne basterà sottrarre al prodotto dei numeri che si trovano nella diagonale principale (in rosso) il prodotto dei numeri che si trovano nella diagonale secondaria (in blu). Con queste considerazioni è piuttosto agevole ricordare la formula del determinante relativo al caso in esame. 😉
Consideriamo ora una matrice {3 \times 3}:
A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}In questo caso per il calcolo del determinante è conveniente utilizzare la regola di Sarrus.
Prolunghiamo anzitutto la matrice ripetendo a destra le prime due colonne:
\begin{bmatrix}a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \begin{matrix}a & b \\ d & e \\ g & h \end{matrix}Consideriamo tutte le diagonali discendenti da sinistra verso destra nella matrice “prolungata” (diagonali principali):
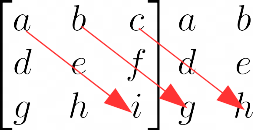
e sommiamo tra loro i prodotti corrispondenti a tali diagonali:
a \cdot e \cdot i + b \cdot f \cdot g + c \cdot d \cdot h
In altre parole, per ogni diagonale dobbiamo considerare il prodotto delle quantità che si trovano nella diagonale stessa.
Ora sottraiamo a quanto appena scritto i prodotti corrispondenti alle diagonali ascendenti da sinistra verso destra, sempre nella matrice “prolungata” (diagonali secondarie):

a \cdot e \cdot i + b \cdot f \cdot g + c \cdot d \cdot h \boxed{-g \cdot e \cdot c - h \cdot f \cdot a -i \cdot d \cdot b}Così in conclusione il determinante di una matrice {3 \times 3} si calcola come:

\small \det \begin{bmatrix}a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} = a \cdot e \cdot i + b \cdot f \cdot g + c \cdot d \cdot h -g \cdot e \cdot c - h \cdot f \cdot a -i \cdot d \cdot bMatrice dei coefficienti di un sistema lineare
Consideriamo un sistema lineare in forma normale di due equazioni in due incognite (brevemente, sistema due per due):
\begin{cases} a_1x+b_1y=k_1 \\ \\ a_2x + b_2y = k_2 \end{cases}La matrice dei coefficienti di un sistema “due per due” è una matrice di due righe per due colonne che contiene ordinatamente i coefficienti che compaiono nei primi membri delle equazioni a sistema:
\begin{bmatrix} a_1 & b_1 \\ a_2 & b_2 \end{bmatrix}Allo stesso modo, dato un sistema lineare di tre equazioni in tre incognite, sempre in forma normale:
\begin{cases} a_1x + b_1y+c_1z= k_1 \\ \\ a_2x+b_2y+c_2z=k_2 \\ \\ a_3x + b_3y+c_3 z = k_3 \end{cases}la corrispondente matrice dei coefficienti si scrive come:
\begin{bmatrix}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{bmatrix}ed è una matrice di tre righe per tre colonne.
Nelle matrici dei coefficienti (sia due per due, sia tre per tre), la prima colonna rappresenta la colonna dei coefficienti dei termini in x, la seconda colonna è la colonna dei coefficienti dei termini in y, mentre la eventuale terza colonna è la colonna dei coefficienti dei termini in z.
La colonna formata da tutti i termini noti, disposti secondo l’ordine del sistema, si dice colonna dei termini noti. Ad esempio, nel caso di un sistema due per due la colonna dei termini noti è:
\begin{matrix}k_1 \\ k_2 \end{matrix}mentre in un sistema tre per tre è:
\begin{matrix}k_1 \\ k_2 \\ k_3 \end{matrix}Introdotte le definizioni fondamentali veniamo alla regola di Cramer nel caso dei sistemi lineari due per due e tre per tre.
Regola di Cramer per i sistemi due per due
Vediamo prima di tutto come risolvere i sistemi lineari con il metodo di Cramer nel caso di sistemi di due equazioni in due incognite.
Consideriamo il sistema di due equazioni in due incognite determinato ridotto in forma normale:
\begin{cases}a_1x+b_1y=k_1 \\ \\ a_2x + b_2y=k_2 \end{cases}Le soluzioni del sistema si possono ricavare utilizzando la regola di Cramer come segue:
x =\dfrac{D_x}{D}= \dfrac{\det \begin{bmatrix}k_1 & b_1 \\ k_2 & b_2 \end{bmatrix}}{\det \begin{bmatrix}a_1 & b_1 \\ a_2 & b_2 \end{bmatrix}}; \qquad y = \dfrac{D_y}{D}= \dfrac{\det \begin{bmatrix}a_1 & k_1 \\ a_2 & k_2 \end{bmatrix}}{\det \begin{bmatrix}a_1 & b_1 \\ a_2 & b_2 \end{bmatrix}}In entrambe le frazioni compare a denominatore il determinante della matrice dei coefficienti del sistema. A numeratore abbiamo invece per la frazione relativa all’incognita {x}, il determinante della matrice dei coefficienti ove è stata sostituita la colonna dei termini in x con la colonna dei termini noti del sistema. Per la frazione relativa all’incognita {y} abbiamo invece al numeratore il determinante della matrice dei coefficienti ove è stata sostituita la colonna dei termini in y con la colonna dei termini noti.
In modo del tutto simile, considerando un sistema lineare di tre equazioni in tre incognite, ancora ridotto in forma normale:
\begin{cases} a_1x + b_1y+c_1z= k_1 \\ \\ a_2x+b_2y+c_2z=k_2 \\ \\ a_3x + b_3y+c_3 z = k_3 \end{cases}le soluzioni si calcolano come:
\small \begin{align*} & x=\dfrac{D_x}{D}=\dfrac{\det \begin{bmatrix}k_1 & b_1 & c_1 \\ k_2 & b_2 & c_2 \\ k_3 & b_3 & c_3 \end{bmatrix}}{\det \begin{bmatrix}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{bmatrix}}; \qquad y = \dfrac{ D_y}{D}=\dfrac{\det \begin{bmatrix}a_1 & k_1 & c_1 \\ a_2 & k_2 & c_2 \\ a_3 & k_3 & c_3 \end{bmatrix}}{\det \begin{bmatrix}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{bmatrix}}; \\ \\ & z=\dfrac{D_z }{D} = \dfrac{\det \begin{bmatrix} a_1 & b_1 & k_1 \\ a_2 & b_2 & k_2 \\ a_3 & b_3 & k_3 \end{bmatrix}}{\det \begin{bmatrix}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{bmatrix}} \end{align*}Esattamente come nel caso dei sistemi due per due, ci ritroviamo al denominatore sempre il determinante della matrice dei coefficienti {D} del sistema. Al numeratore abbiamo invece il determinante di una matrice che si ottiene sostituendo, nella matrice dei coefficienti, alla colonna relativa ai coefficienti dell’incognita da ricavare la colonna dei termini noti.
Vediamo ora come risolvere i sistemi lineari con la regola di Cramer mostrando un paio di esempi, relativi rispettivamente ad un sistema di due equazioni in due incognite e ad un sistema di tre equazioni in tre incognite.
Esempio 1 (risolvere i sistemi lineari con il metodo/regola di Cramer)
Risolvere il seguente sistema di due equazioni in due incognite utilizzando la regola di Cramer:
\begin{cases} 3x-y-10=0 \\ \\ 6x+y-17=0 \end{cases}Anzitutto riconduciamo il sistema alla forma normale. In questo caso è sufficiente trasportare al secondo membro i termini noti presenti in ciascuna equazione:
\begin{cases} 3x-y=10 \\ \\ 6x+y=17\end{cases}Possiamo calcolare separatamente i determinanti necessari. Cominciamo dal determinante della matrice dei coefficienti:
D=\det \begin{bmatrix} 3 & -1 \\ 6 & 1\end{bmatrix} =3 \cdot 1 - (6 \cdot -1) = 3+6=9Osserviamo che nel calcolo del determinante è importante prestare attenzione ai segni. Per non incorrere in errori è bene utilizzare senza parsimonia le parentesi tonde.
Ora calcoliamo il determinante {D_x}, ovvero il determinante di quella matrice che si ottiene sostituendo alla colonna dei coefficienti dei termini in {x} della matrice dei coefficienti {D} la colonna dei termini noti. Osserviamo che per il sistema in esame la colonna dei termini noti è:
\begin{matrix}10 \\ 17 \end{matrix}Così abbiamo:
D_x =\det \begin{bmatrix} 10 & -1 \\ 17 & 1 \end{bmatrix}=10 \cdot 1 - (17 \cdot -1) = 10+17=27In modo del tutto simile possiamo calcolare {D_y}:
D_y = \det \begin{bmatrix}3 & 10 \\ 6 & 17 \end{bmatrix} =3 \cdot 17 - 6 \cdot 10 = 51-60=-9Infine non resta che ricavare la soluzione del sistema, calcolando i valori delle incognite:
x=\dfrac{D_x}{D}=\dfrac{27}{9}=3; \qquad y = \dfrac{D_y}{D}=\dfrac{-9}{9}=-1La soluzione del sistema è in conclusione data dalla coppia di valori:
(3; -1)
Esempio 2 (sistema di tre equazioni in tre incognite con il metodo / regola di Cramer)
Vediamo grazie al seguente esempio come risolvere i sistemi lineari di tre equazioni in tre incognite con il metodo di Cramer:
\begin{cases}x+4y-z=-1 \\ \\ 3x-6y+z = -4 \\ \\ 2y+z=3 \end{cases}Prima di tutto, attenzione. Dobbiamo riscrivere il sistema in forma normale. Qui in particolare non abbiamo gran che da fare, ma dobbiamo prestare attenzione alla terza equazione, nella quale “manca” l’incognita {x}. In questo caso, volendo utilizzare il metodo di Cramer, dobbiamo obbligatoriamente far comparire l’incognita, accompagnandola con un coefficiente uguale a zero:
\begin{cases}x+4y-z=-1 \\ \\ 3x-6y+z = -4 \\ \\ 0x+2y+z=3 \end{cases}A questo punto possiamo applicare il metodo di Cramer. Cominciamo calcolando il determinante della matrice dei coefficienti, utilizzando la regola di Sarrus (ricordiamo: somma dei prodotti delle diagonali discendenti della matrice dei coefficienti prolungata meno somma dei prodotti delle diagonali ascendenti della matrice dei coefficienti prolungata).
Scriviamo la matrice dei coefficienti “prolungata”, evidenziando le diagonali principali (quelle discendenti, in rosso) e le diagonali secondarie (quelle ascendenti, in blu). Ricordiamo che la matrice “prolungata” si ottiene ripetendo le prime due colonne della matrice stessa:
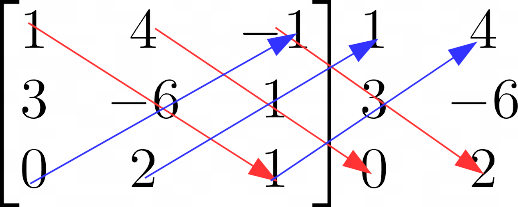
Aiutandoci con lo schema appena rappresentato calcoliamo il determinante {D}:
\small \begin{align*}& D=\det \begin{bmatrix}1 & 4 & -1 \\ 3 & -6 & 1 \\ 0 & 2 & 1 \end{bmatrix} = \\ \\ & = 1 \cdot (-6) \cdot 1 +4 \cdot 1 \cdot 0+(-1) \cdot 3 \cdot 2 -0 \cdot (-6) \cdot (-1) -2 \cdot 1 \cdot 1 -1 \cdot 3 \cdot 4 = \\ \\ & = -6 +0-6-0-2-12=-26\end{align*}Ora calcoliamo i determinanti {D_x, \: D_y} e {D_z}. Teniamo conto che la colonna dei termini noti per il sistema in esame è:
\begin{matrix} -1 \\ -4 \\ 3\end{matrix}Abbiamo:
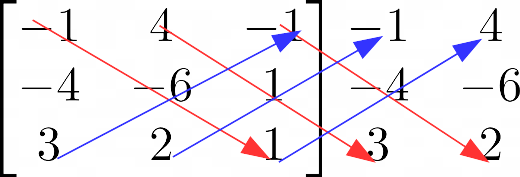
\small \begin{align*} &D_x = \det \begin{bmatrix} -1 & 4 & -1 \\ -4 & -6 & 1 \\ 3 & 2 & 1 \end{bmatrix} =\\ \\ & =-1 \cdot (-6) \cdot 1 +4 \cdot 1 \cdot 3 +(-1) \cdot (-4) \cdot 2 -3 \cdot (-6)\cdot (-1) -2 \cdot 1 \cdot (-1)-1 \cdot (-4) \cdot 4 = \\ \\ & =6+12+8-18+2+16=26 \end{align*} Con ragionamenti del tutto simili è possibile calcolare i rimanenti determinanti:
D_y = \det \begin{bmatrix} 1 & -1 & -1 \\ 3 & -4 & 1 \\ 0 &3 & 1 \end{bmatrix}=-13; \qquad D_z=\det \begin{bmatrix}1 & 4 &-1 \\ 3 & -6 & - 4 \\ 0 & 2 & 3 \\ \end{bmatrix}=-52Otteniamo così per le incognite i seguenti valori:
\begin{align*}&x=\dfrac{D_x}{D}=\dfrac{26}{-26}=-1; \qquad y=\dfrac{D_y}{D}=\dfrac{-13}{-26}=\dfrac{1}{2}; \\ \\ & z=\dfrac{D_z}{D}=\dfrac{-52}{-26} =2 \end{align*}e di conseguenza il sistema assegnato ha per soluzione la terna di valori:
\left(-1; \: \dfrac{1}{2}; \: 2 \right)Come possiamo vedere, risolvere i sistemi lineari con il metodo di Cramer è una procedura piuttosto meccanica. Diversamente dagli altri metodi non richiede particolari ragionamenti. Tuttavia, come già sottolineato più volte occorre prestare particolare attenzione al fatto di non dimenticarsi di ricondurre come prima cosa il sistema assegnato alla forma normale.
NOTA. Per ulteriori dettagli sul metodo di Cramer: metodo di Cramer per sistemi lineari.
Per quanto riguarda questa lezione su come risolvere i sistemi lineari (metodo di sostituzione, di riduzione e di Cramer) è tutto. Nella prossima lezione vedremo il metodo del confronto, che come detto può essere visto come una particolarizzazione del metodo di riduzione.
Come ulteriore approfondimento per ciascun metodo, sono disponibili ulteriori lezioni interamente dedicati ad essi.
Buon proseguimento a tutti voi con SìMatematica! 🙂
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
