Esercizi sul metodo di Cramer

 - 

Sistemi lineari (superiori)

Proponiamo ora una serie di esercizi sul metodo di Cramer (o regola di Cramer), svolti e commentati. Come in tutte le schede di esercizi sui sistemi lineari (sistemi di equazioni di primo grado), ci occuperemo sia del caso di sistemi di due equazioni in due incognite, sia del caso di sistemi di tre equazioni in tre incognite.

Negli esercizi sul metodo di Cramer per sistemi lineari di questa scheda richiameremo tutte le regole da utilizzare. In particolare rivedremo come calcolare i determinanti sia nel semplice caso di matrici quadrate di due righe per due colonne, sia nel caso meno agevole di matrici quadrate aventi tre righe e tre colonne. Ci riferiamo cioè, rispettivamente, alle matrici di due per due elementi e alle matrici di tre per tre elementi.

Ed effettivamente, negli esercizi sul metodo di Cramer l’unica vera difficoltà è data dal calcolo dei determinanti, ovvero quelle quantità numeriche che consentono, se possibile, di risolvere il sistema con delle semplici formule. In particolare, nel caso ad esempio di un sistema determinato di due equazioni in due incognite, una volta noti i determinanti {D, \: D_x} e {D_y} (rivedremo tra un instante cosa sono), i valori delle incognite si ricavano come:

x=\dfrac{D_x}{D}; \qquad y=\dfrac{D_y}{D}

Nel caso di un sistema determinato di tre equazioni in tre incognite abbiamo invece:

x=\dfrac{D_x}{D}; \qquad y=\dfrac{D_y}{D}; \qquad z=\dfrac{D_z}{D}

Ricordiamo che in entrambi i casi la quantità {D} è il determinante della matrice dei coefficienti, ovvero una quantità che si calcola a partire da una “tabella” che contiene i coefficienti delle incognite, nello stesso ordine in cui si presentano nel sistema.

I determinanti {D_x, \: D_y} ed eventualmente {D_z} rappresentano invece i determinanti di particolari matrici che si ottengono sostituendo ordinatamente, nella matrice dei coefficienti, ai coefficienti dei termini nelle incognite {x}, oppure {y}, oppure {z} i termini noti di ciascuna equazione del sistema (in forma normale).

Ora, ciò che ci rimane da rivedere per poter svolgere insieme gli esercizi sul metodo di Cramer per sistemi lineari è proprio il calcolo dei determinanti.

Importante. Prima di applicare il metodo di Cramer è obbligatorio assicurarsi che il sistema dato sia in forma normale, e in caso contrario occorrerà necessariamente ridurlo a tale forma.
Ricordiamo inoltre che è anche fondamentale indicare esplicitamente gli eventuali termini nelle incognite aventi coefficiente zero. Ad esempio se in un’equazione non compare il termine nell’incognita {x} dovremo comunque scrivere il termine {0x}.

Richiamo sui sistemi determinati, indeterminati ed impossibili.

Se il determinante della matrice dei coefficienti {D} è diverso da zero il sistema lineare è determinato. Se invece il determinante {D} è uguale a zero, allora il sistema sarà indeterminato (infinite soluzioni) oppure impossibile (nessuna soluzione).

Ricordiamo in particolare che se il determinante {D} è nullo e sono anche nulli i determinanti {D_x} e {D_y} (ed eventualmente {D_z}) il sistema lineare è indeterminato. Se invece il determinante {D} è ancora nullo ma i determinanti {D_x} e {D_y} (ed eventualmente {D_z}) sono diversi da zero, il sistema lineare è impossibile.

Esercizi con il metodo di Cramer per i sistemi lineari di due equazioni in due incognite: regola da usare

Consideriamo il seguente sistema:

\begin{cases} 2x+3y=-3 \\ \\ 5x+4y+11=0\end{cases}

Per poter scrivere la matrice dei coefficienti è anzitutto necessario ridurre il sistema alla forma normale. Ricordiamo che un sistema lineare è in forma normale se:

• in ciascuna equazione sono presenti esclusivamente termini tra loro non simili;
• al secondo membro di ciascuna equazione abbiamo i soli termini noti;
• nel primo membro di ciascuna equazione le lettere delle incognite compaiono in ordine alfabetico.

Inoltre, dovremo anche riportare esplicitamente gli eventuali termini contenenti le incognite con coefficienti nulli (es., se in un’equazione non è presente il termine nell’incognita {x}, dovremo comunque riportare il termine {0x}).

Nel caso in esame per ridurre il sistema alla forma normale è sufficiente portare al secondo membro il termine numerico {11} nella seconda equazione (ovviamente, cambiandone il segno):

\begin{cases} 2x+3y=-3 \\ \\ 5x+4y=-11\end{cases}

A questo punto il sistema è in forma normale e possiamo scrivere la matrice dei coefficienti:

\begin{bmatrix} 2 & 3 \\ 5 & 4\end{bmatrix}

Osserviamo che abbiamo i coefficienti dei termini contenenti le incognite, nell’esatto ordine in cui compaiono nel sistema.

Abbiamo una matrice di due righe per due colonne (quadrata), e il determinante si ottiene applicando la seguente regola:

D=\det \begin{bmatrix} a & b \\ c & d\end{bmatrix}=a \cdot d - c \cdot b

ovvero nel nostro caso:

D=\det \begin{bmatrix} 2 & 3 \\ 5 & 4\end{bmatrix}=2 \cdot 4 - 5 \cdot 3 = 8-15=-7

Ora, ripartiamo dalla matrice dei coefficienti:

\begin{bmatrix} 2 & 3 \\ 5 & 4\end{bmatrix}

e sostituiamo la sua prima colonna (data dai numeri {2} e {5}, ovvero i coefficienti di tutti i termini in x del sistema) con i termini noti presenti nel sistema, nell’ordine in cui compaiono nel sistema stesso:

\begin{bmatrix} 2 & 3 \\ 5 & 4\end{bmatrix} \quad \Rightarrow \quad \begin{bmatrix} \textbf{-3 } & 3 \\ \\ \textbf{-11} & 4\end{bmatrix}

Il corrispondente determinante {D_x} si calcola con la stessa regola utilizzata per il calcolo del determinante della matrice dei coefficienti:

D_x=\det \begin{bmatrix} {-3 } & 3 \\ \\ {-11} & 4\end{bmatrix}=-3 \cdot 4 - (-11) \cdot 3=-12+33=21

Ora, riprendiamo ancora la matrice dei cofficienti:

\begin{bmatrix} 2 & 3 \\ 5 & 4\end{bmatrix}

Stavolta sostituiamo la seconda colonna (ovvero la colonna che contiene tutti i coefficienti dei termini nell’incognita y) sempre con i termini noti del sistema, anche in questo caso nello stesso ordine in cui compaiono nel sistema:

\begin{bmatrix} 2 & \textbf{-3} \\ 5 & \textbf{-11}\end{bmatrix}

Utilizzando ancora la stessa regola calcoliamo a questo punto il determinante della matrice appena scritta, ovvero {D_y}:

D_y=\det  \begin{bmatrix} 2 & {-3} \\ 5 & {-11}\end{bmatrix}=2\cdot(-11)-5 \cdot(-3)=-22+15=-7

A questo punto abbiamo tutti gli ingredienti per poter ricavare i valori delle incognite:

x=\dfrac{D_x}{D}=\dfrac{21}{-7}=-3; \qquad y=\dfrac{D_y}{D}=\dfrac{-7}{-7}=1

Così in conclusione il sistema è determinato ed ammette come soluzione la coppia ordinata {(x, \:y)}:

(-3, \:1 )

Esercizi sul metodo di Cramer per sistemi lineari di tre equazioni in tre incognite: regola da usare

Il procedimento per svolgere gli esercizi sul metodo di Cramer per sistemi lineari di tre equazioni in tre incognite è del tutto simile a quanto visto nel caso precedente. L’unica differenza è data dalla regola per il calcolo dei determinanti.

La regola che qui proponiamo è la regola di Sarrus:

\small \det \begin{bmatrix} a & b & c \\ d & e &f \\ g & h & i\end{bmatrix}= a \cdot e \cdot i + b \cdot f \cdot g +c \cdot d \cdot h - g \cdot e \cdot c -h \cdot f \cdot a - i \cdot d \cdot b

Per ricordare agevolmente la regola, basta prima di tutto ricopiare di seguito alla matrice le sue prime due colonne:

 \begin{bmatrix} a & b & c \\ d & e &f \\ g & h & i\end{bmatrix} \: \: \begin{matrix}a & b \\ d & e \\ g & h\end{matrix}

Ora immaginiamo di avere delle diagonali, discendenti (in rosso) e ascendenti (in blu). Abbiamo cioè tre diagonali che si muovono verso il basso procedendo da sinistra verso destra, e delle diagonali che sempre procedendo da sinistra verso destra si muovono verso l’alto:

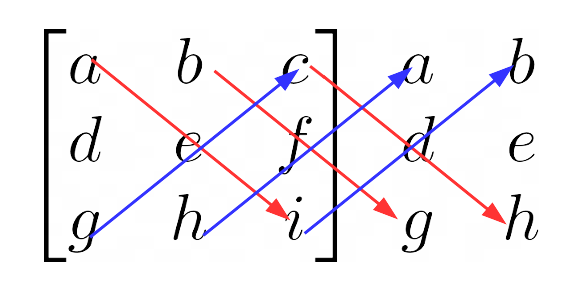
Ora non resta che sommare tra loro ciascuno dei prodotti dei termini presenti in ognuna delle diagonali discendenti (in rosso), sottraendo poi ciascuno dei prodotti dei termini presenti in ognuna delle diagonali ascendenti (in blu). La quantità che otteniamo è proprio il determinante della matrice di partenza. Così ritroviamo la regola:

\small \det \begin{bmatrix} a & b & c \\ d & e &f \\ g & h & i\end{bmatrix}= \overbrace{a \cdot e \cdot i + b \cdot f \cdot g +c \cdot d \cdot h}^{\text{diagonali discendenti (rosso)}} - \overbrace{g \cdot e \cdot c -h \cdot f \cdot a - i \cdot d \cdot b}^{\text{diagonali ascendenti (blu)}}

All’inizio è bene aggiungere su carta le prime due colonne aggiuntive alla matrice “tre per tre” della quale calcolare il determinante. Con il tempo tuttavia sarà possibile applicare la regola di Sarrus direttamente a partire dalla matrice così come è, senza il bisogno di ripetere le prime due colonne.

A questo punto disponiamo di tutti i richiami teorici necessari per poter svolgere gli esercizi sui sistemi lineari con il metodo di Cramer.

Esercizi sul metodo di Cramer per sistemi lineari: svolgimenti

Prima parte: sistemi lineari di due equazioni in due incognite

Esercizio 1

Risolviamo insieme il seguente sistema lineare, utilizzando il metodo di Cramer (o regola di Cramer):

\begin{cases} 5x-2y=7 \\ \\ 5y-3x = 11 \end{cases}

Prima di tutto, attenzione. Il sistema non è in forma normale. Infatti, nella seconda equazione le lettere delle incognite non si presentano in ordine alfabetico.

Disponendo allora opportunamente i termini della seconda equazione il sistema diviene in forma normale:

\begin{cases} 5x-2y=7 \\ \\ -3x+5y= 11 \end{cases}

Soltanto dopo essersi assicurati che il sistema è in forma normale è possibile scrivere la matrice dei coefficienti e quindi procedere al calcolo dei determinanti.

Scriviamo la matrice dei coefficienti (“tabella” con i coefficienti dei termini contenenti le incognite, nello stesso ordine in cui compaiono nel sistema):

\begin{bmatrix} 5 & -2 \\ -3 & 5\end{bmatrix}

Calcoliamone il determinante:

\det \begin{bmatrix} 5 & -2 \\ -3 & 5\end{bmatrix}=5 \cdot 5 - (-3) \cdot (-2)=25-6=19

Ora, consideriamo la matrice che si ottiene sostituendo alla prima colonna della matrice dei coefficienti i termini noti presenti nel sistema (nell’ordine in cui si presentano). In altre parole si tratta di sostituire ordinatamente nella matrice i coefficienti dei termini nell’incognita {x} con i termini noti presenti in ciascuna equazione del sistema. Otteniamo la seguente matrice:

\begin{bmatrix} \textbf{7}  & -2 \\ \textbf{11} & 5\end{bmatrix}

Calcoliamone il determinante. Questo si chiama {D_x}, ove nel pedice abbiamo la lettera dell’incognita relativa ai coefficienti che abbiamo sostituito con i termini noti:

D_x=\det \begin{bmatrix} 7 & -2 \\ 11 & 5 \end{bmatrix}=7\cdot 5 -11 \cdot (-2)=35+22=57

Ora, riprendiamo la matrice dei coefficienti e sostituiamo la seconda colonna con i termini noti del sistema, ordinatamente:

\begin{bmatrix} 5 & \textbf{7} \\ -3 & \textbf{11} \end{bmatrix}

Calcoliamo a questo punto il determinante {D_y}. Osserviamo che stavolta nel pedice è indicata l’incognita {y}, poiché nella matrice dei coefficienti abbiamo effettivamente sostituito con i termini noti i coefficienti relativi all’incognita {y}.

Per il determinante abbiamo:

D_y=\det \begin{bmatrix} 5 & {7} \\ -3 & {11} \end{bmatrix}=5 \cdot 11 - (-3) \cdot 7 =55+21=76

Ora abbiamo tutti gli ingredienti che ci servono per calcolare i valori delle incognite {x} e {y}:

x=\dfrac{D_x}{D}=\dfrac{57}{19}=3; \qquad y=\dfrac{D_y}{D}=\dfrac{76}{19}=4

Così il sistema è determinato ed ha per soluzione la coppia ordinata {(x, \: y)}:

(3, \: 4)

Esercizio 2

Proseguiamo gli esercizi sul metodo di Cramer relativi a sistemi di due equazioni in due incognite con il seguente:

\begin{cases} 4(x-y)=5+2x+y \\ \\ 5(x-2y)=\dfrac{8x+17}{2}\end{cases}

Osserviamo che il sistema non è in forma normale. Infatti, abbiamo la presenza di calcoli da sviluppare e sicuramente ci ritroveremo con dei termini non simili. Inoltre, sarà necessario trasportare opportunamente i termini. Abbiamo:

\small \begin{align*} & \begin{cases} 4x-4y=5+2x+y \\ \\ 5x-10y=\dfrac{8x+17}{2}\end{cases} \quad \Rightarrow \quad \begin{cases} 4x-2x-4y-y=5 \\ \\ 5x-10y-\dfrac{8}{2}x=\dfrac{17}{2}\end{cases} \quad  \Rightarrow \\ \\ &\Rightarrow  \begin{cases}2x-5y=5 \\ \\ x-10y=\dfrac{17}{2} \end{cases}   \end{align*}

A questo punto il sistema è ridotto alla forma normale e possiamo cominciare ad applicare il metodo di Cramer scrivendo la matrice dei coefficienti:

\begin{bmatrix} 2 & -5 \\ 1 & - 10\end{bmatrix}

Calcoliamo il determinante della matrice dei coefficienti:

D=\det \begin{bmatrix} 2 & -5 \\ 1 & - 10\end{bmatrix}=2 \cdot (-10) - 1 \cdot (-5)=-20+5=-15

Ora, sostituiamo la prima colonna della matrice dei coefficienti con i termini noti del sistema:

\begin{bmatrix} \textbf{5} & -5 \\ \textbf{17/2} & - 10\end{bmatrix}

Calcoliamo il determinante della matrice così ottenuta:

\begin{align*} & D_x = \det \begin{bmatrix} 5 & - 5 \\ 17/2  & -10 \end{bmatrix}=5 \cdot (-10)-\dfrac{17}{2} \cdot (-5)= \\ \\ & =-50+\dfrac{85}{2}= -\dfrac{15}{2}\end{align*}

Ora, riprendiamo la matrice dei coefficienti e sostituiamo la seconda colonna (coefficienti dell’incognita {y}) con i termini noti del sistema:

\begin{bmatrix} 2 & \textbf{5}\\ 1 & \textbf{17/2}\end{bmatrix}

Calcoliamone il determinante:

D_y=2 \cdot \dfrac{17}{2}-1 \cdot 5 = 17-5=12

E’ ora possibile calcolare i valori delle incognite {x} e {y}:

\begin{align*} & x=\dfrac{D_x}{D}=\dfrac{-\frac{15}{2}}{-15}=-\dfrac{15}{2} \cdot \left( -\dfrac{1}{15}\right)=\dfrac{1}{2}; \\ \\ & y=\dfrac{D_y}{D}=\dfrac{12}{-15}=-\dfrac{4}{5}\end{align*}

Così in conclusione il sistema è determinato ed ammette come soluzione la coppia:

\left( \dfrac{1}{2}, \: -\dfrac{4}{5}\right)

Esercizio 3

Risolviamo ora il seguente sistema:

\begin{cases} 2x-y=\dfrac{2}{3} \\ \\ (x+3)^2=y+2(2x+7)+x^2\end{cases}

Riconduciamo anzitutto il sistema alla forma normale:

\begin{cases} 2x-y=\dfrac{2}{3} \\ \\ \cancel{x^2}+6x+9=y+4x+14+\cancel{x^2}\end{cases} \quad \Rightarrow \quad \begin{cases}  2x-y=\dfrac{2}{3} \\ \\ 2x-y=5\end{cases}

Già ora ci accorgiamo che il sistema è impossibile. Infatti, la quantità {2x-y} non può essere uguale a due diversi numeri.

Tuttavia, come ulteriore conferma vediamo cosa succede per i determinanti (il loro calcolo avviene con le regole viste negli esercizi precedenti).

\small \begin{align*} & \begin{align*} &\end{align*}D=\det \begin{bmatrix} 2 & -1 \\ 2 & -1\end{bmatrix}=2 \cdot (-1)-2 \cdot (-1)=-2+2=0 ; \\ \\ & D_x = \det \begin{bmatrix} 2/3 & -1 \\ 5 & -1\end{bmatrix}=\dfrac{2}{3}\cdot (-1)-5 \cdot (-1)=\dfrac{13}{3} \neq  0; \\ \\ &D_y = \det \begin{bmatrix} 2 & 2/3 \\ 2 & 5\end{bmatrix} = 2 \cdot 5 - 2 \cdot \dfrac{2}{3}=10-\dfrac{4}{3}=\dfrac{27}{3}\neq 0\end{align*}

Effettivamente ci ritroviamo con la condizione:

D = 0 \quad \wedge \quad D_x\neq 0 \quad \wedge \quad  D_y \neq 0 

che corrisponde al caso di un sistema lineare impossibile.

Ricordiamo che il simbolo {\wedge} significa “e contemporaneamente” e si riferisce all’operazione di congiunzione logica (AND).

Esercizio 4

Proseguiamo gli esercizi sul metodo di Cramer per i sistemi di due equazioni in due incognite:

\begin{cases} 5(x-2y)=4 \\ \\ 5(x+2y)+2(x-4y)-4=0\end{cases}

Riconduciamo anzitutto il sistema alla forma normale:

\begin{cases} 5x-10y=4 \\ \\ 5x+10y+2x-8y=4\end{cases}

ovvero, sommando i termini simili:

\begin{cases} 5x-10y=4 \\ \\ 7x+2y=4\end{cases}

Ora il sistema è in forma normale ed è possibile scrivere di conseguenza la matrice dei coefficienti:

\begin{bmatrix} 5 & -10 \\ 7 & 2\end{bmatrix}

Calcoliamo il determinante della matrice dei coefficienti:

D=\det  \begin{bmatrix} 5 & -10 \\ 7 & 2\end{bmatrix} = 5 \cdot 2 - 7 \cdot (-10) = 10+70=80

Veniamo ora ai determinanti {D_x} e {D_y}:

\begin{align*} & D_x =\det  \begin{bmatrix} 4 & -10 \\ 4 & 2\end{bmatrix}=4 \cdot 2 - 4 \cdot (-10)=8+40=48; \\ \\ & D_y=\det \begin{bmatrix} 5 & 4 \\ 7 & 4 \end{bmatrix}=5 \cdot 4 - 7 \cdot 4 = 20-28=-8 \end{align*}

Abbiamo così per i valori delle incognite, utilizzando le formule del metodo di Cramer per i sistemi di due equazioni in due incognite:

\begin{align*} & x=\dfrac{D_x}{D}=\dfrac{48}{80}=\dfrac{6}{10}=\dfrac{3}{5};\\ \\ & y = \dfrac{D_y}{D}=\dfrac{-8}{80}=-\dfrac{1}{10} \end{align*}

Il sistema è quindi determinato ed ha come soluzione la coppia:

\left( \dfrac{3}{5}, \: -\dfrac{1}{10}\right)

Esercizio 5

Vediamo un ultimo esercizio sul metodo di Cramer relativamente ai sistemi lineari di due equazioni in due incognite, per poi passare al caso di sistemi lineari di tre equazioni in tre incognite.

Risolviamo il seguente sistema:

\begin{cases} 3x-6y=-5 \\ \\ 4(x+y)=1-x\end{cases}

Cominciamo riducendo il sistema alla forma normale:

\begin{cases} 3x-6y=-5 \\ \\ 4x+4y=1-x\end{cases} \quad \Rightarrow \quad \begin{cases} 3x-6y=-5 \\ \\ 5x+4y=1\end{cases}

Ora il sistema è in forma normale e possiamo procedere al calcolo dei determinanti:

\begin{align*} & D=\det \begin{bmatrix} 3 & -6 \\ 5 & 4 \end{bmatrix}=3 \cdot 4 -5  \cdot (-6)=12+30=42; \\ \\ & D_x=\det \begin{bmatrix} -5 & -6 \\ 1 & 4 \end{bmatrix} = -5 \cdot 4 - 1 \cdot (-6) =-20+6=-14; \\ \\ & D_y=\det \begin{bmatrix} 3 & -5 \\ 5 & 1 \end{bmatrix} = 3 \cdot 1 - 5 \cdot (-5)=3+25=28\end{align*}

In conclusione otteniamo i valori delle incognite:

x=\dfrac{D_x}{D}=\dfrac{-14}{42}=-\dfrac{1}{3}; \qquad y = \dfrac{D_y}{D}=\dfrac{28}{42}=\dfrac{4}{6}=\dfrac{2}{3}

a cui corrisponde la coppia soluzione del sistema:

 \left( -\dfrac{1}{3}, \: \dfrac{2}{3}\right)

Seconda parte: esercizi sul metodo di Cramer relativi a sistemi di tre equazioni in tre incognite

Vediamo ora degli esercizi sul metodo di Cramer per i sistemi lineari di tre equazioni in tre incognite. Come già anticipato, l’unica differenza rispetto al caso precedente è praticamente data dal dover calcolare dei determinanti di matrici di tre per tre elementi (ovvero matrici composte da tre righe ciascuna avente tre elementi).

Esercizio 6

Risolvere utilizzando il metodo di Cramer il seguente sistema lineare:

\begin{cases} x+2y-z=5 \\ \\ x+z=\dfrac{3}{2}(y-z+1) \\ \\ 2y-5z=x-1\end{cases}

Riduciamo anzitutto il sistema alla forma normale. La prima equazione già si presenta nella forma richiesta. Lavoriamo sulle altre due equazioni:

\small \begin{cases} x+2y-z=5 \\ \\ x+z=\dfrac{3}{2}y-\dfrac{3}{2}z+\dfrac{3}{2} \\ \\x-2y+5z=1\end{cases} \quad \Rightarrow \quad \begin{cases} x+2y-z=5 \\ \\ x+z-\dfrac{3}{2}y+\dfrac{3}{2}z=\dfrac{3}{2} \\ \\x-2y+5z=1\end{cases}

e quindi, sommando i termini simili nella seconda equazione:

\begin{cases} x+2y-z=5 \\ \\x-\dfrac{3}{2}y+\dfrac{5}{2}z=\dfrac{3}{2} \\ \\ x-2y+5z=1\end{cases}

A questo punto possiamo calcolare i determinanti. Ritrovandoci delle matrici “tre per tre” dovremo utilizzare la regola di Sarrus.

Per prima cosa scriviamo la matrice dei coefficienti:

\begin{bmatrix} 1 & 2 & -1 \\1 & \small{-3/2} & \small{5/2} \\ 1 & -2  & 5\end{bmatrix}

Adesso calcoliamo il determinante della matrice dei coefficienti mediante la regola di Sarrus.

Ricopiamo prima di tutto le prime due colonne della matrice di seguito alla matrice stessa:

\begin{bmatrix} 1 & 2 & -1 \\1 & \small{-3/2} & \small{5/2} \\ 1 & -2  & 5\end{bmatrix} \: \: \begin{matrix} 1 & 2 \\ 1 & \small{-3/2} \\ 1 & -2 \end{matrix}

Ora individuiamo le diagonali discendenti (che indicheremo in rosso) e le diagonali ascendenti (che indicheremo in blu):

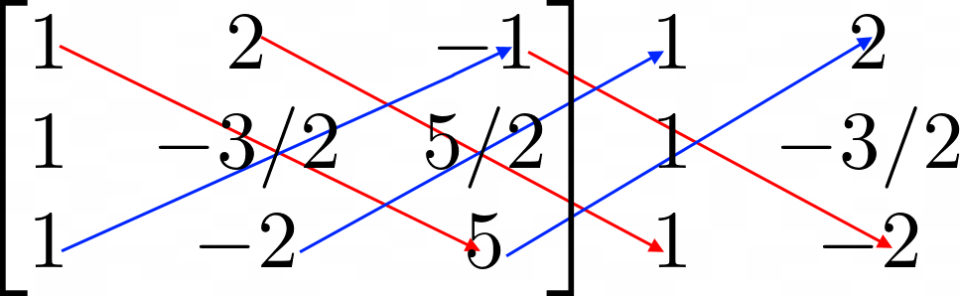
Procediamo considerando per ogni diagonale il prodotto degli elementi che si trovano in essa. In particolare, dovremo sommare tra loro i prodotti degli elementi che si trovano in ciascuna diagonale discendente (in rosso), sottraendo poi ciascun prodotto fra gli elementi di ciascuna diagonale ascendente (in blu). Il numero che così otteniamo è il determinante della matrice data. Abbiamo:

\begin{align*} & D=\det \begin{bmatrix} 1 & 2 & -1 \\1 & -\frac{3}{2} &\frac{5}{2} \\ 1 & -2  & 5\end{bmatrix}= \\ \\ & =1 \cdot \left( -\dfrac{3}{2}\right) \cdot 5 +2 \cdot \dfrac{5}{2} \cdot 1 +(-1) \cdot 1 \cdot (-2) + \\ \\ & -1 \cdot (-3/2) \cdot (-1)-(-2) \cdot \dfrac{5}{2} \cdot 1 - 5 \cdot 1 \cdot 2 =\\ \\ & =-\dfrac{15}{2}+5+2-\dfrac{3}{2}+5-10=-7 \end{align*}

Ora, riprendiamo la matrice dei coefficienti e sostituiamo alla sua prima colonna i termini noti del sistema. In pratica si tratta di sostituire ai coefficienti dell’incognita {x} presenti nella matrice i termini noti delle equazioni a sistema, nell’ordine in cui compaiono.

\begin{bmatrix} \textbf{5} & 2 & -1 \\\textbf{3/2}& \small{-3/2} & \small{5/2} \\ \textbf{1} & -2  & 5\end{bmatrix}

Il determinante {D_x} di questa matrice si calcola ancora con la regola di Sarrus, allo stesso modo del determinante {D} della matrice dei coefficienti:

\begin{align*} & D_x=\det \begin{bmatrix} {5} & 2 & -1 \\{3/2}& \small{-3/2} & \small{5/2} \\ {1} & -2  & 5\end{bmatrix}= \\ \\ & =5 \cdot \left( -\dfrac{3}{2}\right) \cdot 5 +2 \cdot \dfrac{5}{2} \cdot 1 + (-1) \cdot \dfrac{3}{2} \cdot (-2)+ \\ \\ & -1 \cdot \left( -\dfrac{3}{2}\right)\cdot(-1)-(-2) \cdot \dfrac{5}{2} \cdot 5-5 \cdot \dfrac{3}{2} \cdot 2 = \\ \\ & =-\dfrac{75}{2}+5+3-\dfrac{3}{2} +25-15=\\ \\ & =-39+8+10=-21\end{align*}

Ora, riprendiamo la matrice dei coefficienti e sostituiamo stavolta la seconda colonna con i termini noti del sistema. Ciò corrisponde a sostituire ordinatamente i coefficienti dei termini nell’incognita {y} con i termini noti:

\begin{bmatrix} 1 & \textbf{5} & -1 \\1 & \textbf{3/2} & \small{5/2} \\ 1 & \textbf{1}  & 5\end{bmatrix}

Calcoliamone il determinante {D_y}, sempre utilizzando la regola di Sarrus:

\small \begin{align*} & D_y=\det \begin{bmatrix} 1 &5 & -1 \\1 & {3/2} & \small{5/2} \\ 1 & {1}  & 5\end{bmatrix} = \\ \\ & =1 \cdot \dfrac{3}{2} \cdot 5+5 \cdot \dfrac{5}{2} \cdot 1 + (-1) \cdot 1 \cdot 1 -1 \cdot \dfrac{3}{2} \cdot (-1)-1 \cdot \dfrac{5}{2} \cdot 1 -5 \cdot 1 \cdot 5 = \\ \\ & = \dfrac{15}{2}+\dfrac{25}{2}-1+\dfrac{3}{2}-\dfrac{5}{2}-25=-7\end{align*}

Ora, dato che stiamo risolvendo un sistema di tre equazioni in tre incognite, abbiamo ancora da calcolare un determinante. Si tratta in particolare di calcolare {D_z}, ovvero il determinante della matrice che si ottiene sostituendo la terza colonna della matrice dei coefficienti con i termini noti del sistema. In pratica si tratta di sostituire i coefficienti dei termini nell’incognita {z} con i termini noti. Abbiamo:

\small \begin{align*} &D_z=\det \begin{bmatrix} 1 & 2 & \textbf{5}\\1 & \small{-3/2} & \textbf{3/2} \\ 1 & -2  & \textbf{1}\end{bmatrix}= \\ \\ & =1 \cdot \left( -\dfrac{3}{2}\right) \cdot 1 + 2 \cdot \dfrac{3}{2} \cdot 1 +5 \cdot 1 \cdot (-2)-1 \cdot \left( -\dfrac{3}{2}\cdot \right) \cdot 5 -(-2) \cdot \dfrac{3}{2}\cdot 1-1 \cdot 1 \cdot 2= \\ \\ & =-\dfrac{3}{2}+3-10+\dfrac{15}{2}+3-2=0\end{align*}

A questo punto non resta che calcolare i valori delle incognite, tenendo conto delle seguenti formule, valide per il metodo di Cramer applicato ai sistemi lineari di tre equazioni in tre incognite:

x=\dfrac{D_x}{D}; \qquad y=\dfrac{D_y}{D}; \qquad z=\dfrac{D_z}{D}

Nel nostro caso otteniamo per le incognite i seguenti valori:

\begin{align*} &x=\dfrac{D_x}{D}=\dfrac{-21}{-7}=3; \qquad y=\dfrac{D_y}{D}=\dfrac{-7}{-7} = 1; \\ \\ & z=\dfrac{D_z}{D}=\dfrac{0}{-7}=0\end{align*}

Così in conclusione il sistema lineare dato è determinato ed ha come soluzione la terna ordinata di valori {(x, \: y, z)} seguente:

(3, \: 1, \: 0)

Esercizio 7

Proseguiamo gli esercizi sul metodo di Cramer per sistemi di tre equazioni in tre incognite con il seguente:

\begin{cases}2x+2y=1-z \\ \\ 3x-3y-3=z-x \\ \\ 3-2z=2x+2y \end{cases}

Prima di tutto, non dimentichiamocene mai prima di utilizzare il metodo di Cramer, dobbiamo ridurre il sistema alla forma normale. In questo caso non lo è poiché abbiamo dei termini simili ed inoltre occorre trasportare opportunamente i termini. Abbiamo:

\begin{cases}2x+2y+z=1\\ \\ 4x-3y-z=3 \\ \\ 2x+2y+2z=3 \end{cases}

Calcoliamo ora i determinanti, utilizzando le stesse regole viste negli esercizi precedenti:

\small \begin{align*} &D=\det \begin{bmatrix} 2 & 2 & 1 \\ 4 &-3 & -1 \\ 2 & 2 & 2\end{bmatrix}= \\ \\ & =2 \cdot(-3) \cdot 2 + 2 \cdot (-1) \cdot 2 +1 \cdot 4 \cdot 2 - 2 \cdot (-3) \cdot 1 - 2 \cdot (-1) \cdot 2 - 2 \cdot 4 \cdot 2 = \\ \\ & =-12-4+8+6+4-16=-14; \\ \\ & D_x= \det \begin{bmatrix} \textbf{1} & 2 & 1 \\ \textbf{3} & -3 & -1 \\ \textbf{3} & 2 & 2 \end{bmatrix} = \\ \\ & =1 \cdot (-3) \cdot 2 + 2 \cdot (-1) \cdot 3 + 1 \cdot 3 \cdot 2 - 3 \cdot (-3) \cdot 1 -2 \cdot (-1) \cdot 1 - 2 \cdot 3 \cdot 2 = \\ \\ & =-6-6+6+9+2-12=-7; \\ \\& D_y =\det \begin{bmatrix} 2 & \textbf{1} &  1 \\ 4 & \textbf{3} & -1 \\ 2 & \textbf{3} & 2 \end{bmatrix}= \\ \\ & = 2 \cdot 3 \cdot 2 + 1 \cdot (-1) \cdot 2 + 1 \cdot 4 \cdot 3 -2 \cdot 3 \cdot 1 - 3 \cdot (-1) \cdot 2 -2 \cdot 4 \cdot 1=\\ \\ & =12-2+12-6+6-8=14; \\  \\  & D_z = \det \begin{bmatrix} 2 & 2 & \textbf{1} \\ 4 &-3 & \textbf{3} \\ 2 & 2 &\textbf{3} \end{bmatrix} = \\ \\ & = 2 \cdot (-3) \cdot 3 +2 \cdot 3 \cdot 2 +  1 \cdot 4 \cdot 2 -2 \cdot (-3) \cdot 1 - 2 \cdot 3 \cdot 2-3 \cdot 4 \cdot 2 = \\ \\ & =-18+12+8+6-12-24=-28\end{align*}

Ora che abbiamo tutti i determinanti possiamo calcolare i valori delle incognite:

\begin{align*} & x=\dfrac{D_x}{D}=\dfrac{-7}{-14}=\dfrac{1}{2}; \qquad y=\dfrac{D_y}{D}=\dfrac{14}{-14}=-1; \\ \\ & z=\dfrac{D_z}{D}=\dfrac{-28}{-14}=2 \end{align*}

Il sistema è dunque determinato ed ha come soluzione la terna ordinata di valori:

\left( \dfrac{1}{2}, \: -1, \: 2\right)

Esercizio 8

Veniamo ora all’ultimo degli esercizi sul metodo di Cramer di questa scheda, sempre relativo ai sistemi di tre equazioni in tre incognite. Omettiamo le spiegazioni poiché ormai dovrebbe essere tutto chiaro, e vi invitiamo a svolgere da soli l’esercizio per poi confrontare il vostro svolgimento con quello qui proposto. 😉

\begin{cases} x+\dfrac{5}{4}y+\dfrac{1}{2}z=-\dfrac{1}{4} \\ \\ \dfrac{1}{3}x-\dfrac{1}{2}y+\dfrac{2}{3}z=\dfrac{1}{6} \\ \\ x-\dfrac{1}{4}y+z=0\end{cases}

Il sistema è già dato in forma normale. Calcoliamo i determinanti:

\begin{align*} & D=\det \begin{bmatrix}1 & 5/4 & 1/2 \\ 1/3 & -1/2 & 2/3 \\ 1 & -1/4 & 1 \end{bmatrix}=\dfrac{7}{24}; \\ \\ &D_x=  \det \begin{bmatrix} \textbf{-1/4} & 5/4 & 1/2 \\ \textbf{1/6} &-1/2 & 2/3 \\ \textbf{0} & -1/4 & 1\end{bmatrix}=-\dfrac{7}{48}; \\ \\ & D_y = \det \begin{bmatrix} 1 & \textbf{-1/4}
 & 1/2 \\ 1/3 & \textbf{1/6} & 2/3 \\ 1 & \textbf{0} & 1\end{bmatrix}=0; \\ \\ & D_z= \det \begin{bmatrix} 1 & 5/4 &\textbf{-1/4} \\ 1/3 & -1/2 & \textbf{1/6} \\ 1 & -1/4 & \textbf{0}\end{bmatrix}=\dfrac{7}{48}\end{align*}

A questo punto possiamo calcolare i valori delle incognite:

\begin{align*} &x=\dfrac{D_x}{D}=\dfrac{-\dfrac{7}{48}} {\dfrac{7}{24}}=-\dfrac{7}{48} \cdot \dfrac{24}{7}=-\dfrac{1}{2}; \\ \\ & y=\dfrac{D_y}{D}=0; \\ \\ & z=\dfrac{D_z}{D}=\dfrac{\dfrac{7}{48}}{\dfrac{7}{24}}=\dfrac{7}{48}\cdot\dfrac{24}{7}=\dfrac{1}{2}\end{align*}

Il sistema è quindi determinato ed ammette quindi come soluzione la terna:

\left( -\dfrac{1}{2}, \: 0, \: \dfrac{1}{2}\right)

Conclusioni

Per quanto riguarda questa scheda di esercizi sul metodo di Cramer per i sistemi lineari di due equazioni in due incognite e di tre equazioni in tre incognite è tutto. Buono studio a tutti voi con SìMatematica!