Esercizi sulla retta per due punti

 - 

Esercizi sulla retta nel piano e coordinate cartesiane

Proponiamo in questa scheda una serie di esercizi sulla retta passante per due punti del piano cartesiano. In particolare, i possibili metodi da utilizzare per scrivere l’equazione di una retta passante per due punti dati (non allineati né orizzontalmente né verticalmente) sono i seguenti:

• calcolo del coefficiente angolare e calcolo dell’ordinata all’origine, quest’ultimo sostituendo le coordinate di uno dei due punti nell’equazione {y=mx+q}, da cui {q=y-mx};
• calcolo del coefficiente angolare e quindi utilizzo dell’equazione della retta per un punto con pendenza nota: {y-y_0 = m(x-x_0)};
• utilizzo dell’equazione di una retta passante per due punti: {\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}};
• infine, utilizzo delle formule per ricavare il coefficiente angolare e l’ordinata all’origine della retta a partire dalle coordinate di due punti appartenenti alla retta stessa.

Nel corso di questa scheda presenteremo esercizi sulla retta per due punti che utilizzano ciascuno dei metodi appena elencati.

La scelta del metodo da preferire va fatta regolandosi in base alle indicazioni dell’insegnante e comunque utilizzando il metodo che si ritiene più comodo. In particolare, la scelta dipende anche dalle formule che in un dato momento si riescono a ricordare. I primi due metodi nell’elenco sono sicuramente quelli che richiedono un minor sforzo nel ricordare le formule. L’ultimo metodo è sicuramente quello più scomodo da questo punto di vista, poiché la formula per il calcolo dell’ordinata all’origine di una retta a partire dalle coordinate di due suoi punti non è certo una delle formule più facili da ricordare.

Ma vediamo nell’ordine i vari metodi in azione in questa serie di esercizi sulla retta passante per due punti.

Esercizi svolti e commentati sulla retta passante per due punti

Importante. Per gli esercizi a seguire valgono le ipotesi {x_1 \neq x_2} e {y_1 \neq y_2}, ovvero i due punti {P_1} e {P_2} dati non sono allineati né orizzontalmente, né verticalmente. Alla fine della scheda presenteremo comunque degli esercizi nei quali i due punti sono allineati verticalmente oppure orizzontalmente.

Prima parte: metodo del coefficiente angolare e ordinata all’origine ricavata dall’equazione y=mx+q

Esercizio 1

Scrivere l’equazione in forma implicita della retta passante per i due punti {P_1=(x_1,y_1)=(2,1)} e {P_2=(x_2, y_2)=(7,5)}.

Cominciamo calcolando il coefficiente angolare:

m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{5-1}{7-2}=\dfrac{4}{5}

A questo punto sostituiamo il valore del coefficiente angolare appena ottenuto e ad esempio le coordinate del punto {P_1} nell’equazione {y=mx+q}, esplicitando {q}:

y_1=mx_1+q \quad \Rightarrow \quad q=y_1-mx_1=1-\dfrac{4}{5} \cdot 2=-\dfrac{3}{5}

Abbiamo quindi {m=\dfrac{4}{5}} e {q=-\dfrac{3}{5}}. Così l’equazione della retta passante per i due punti dati, nella forma esplicita, è data da:

y=\dfrac{4}{5}x-\dfrac{3}{5}

Poiché il testo richiede l’equazione nella forma implicita, trasportiamo tutti i termini al primo membro:

y-\dfrac{4}{5}x+\dfrac{3}{5}=0

Ordiniamo i termini in modo da ricondurci alla forma {ax+by+c=0}:

-\dfrac{4}{5}x+y+\dfrac{3}{5}=0

Invertiamo per un discorso estetico i segni di tutti i termini:

\dfrac{4}{5}x-y-\dfrac{3}{5}=0

A questo punto mettiamo tutti i termini a denominatore comune, per poi eliminare direttamente il denominatore (questo è infatti un numero):

\dfrac{4x-5y-3}{\cancel{5}}=0

Otteniamo così in conclusione la seguente equazione in forma implicita:

4x-5y-3=0

Esercizio 2

Scrivere l’equazione in forma esplicita della retta passante per i due punti {P_1=(1,1)} e {P_2=\left( \dfrac{1}{3}, 3\right)}.

Cominciamo calcolando il coefficiente angolare:

m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{3-1}{\frac{1}{3}-1}=\dfrac{2}{-\frac{2}{3}}=2\cdot\left( -\dfrac{3}{2}\right)=-3

Per l’ordinata all’origine abbiamo, prendendo ad esempio le coordinate del punto {P_1}:

q=y_1-mx_1=1-(-3)\cdot1=4

Così in conclusione l’equazione in forma esplicita passante per i due punti dati è:

y=-3x+4

Seconda parte: esercizi sull’equazione della retta passante per due punti mediante calcolo del coefficiente angolare ed uso dell’equazione con punto e pendenza

Esercizio 3

Scrivere l’equazione in forma esplicita della retta passante per i due punti {P_1=(0,1)} e {P_2=(1,3)}.

Cominciamo calcolando il coefficiente angolare:

m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{3-1}{1-0}=2

A questo punto utilizziamo l’equazione di una retta passante per un punto e con coefficiente angolare noto, ovvero l’equazione {y-y_0=m(x-x_0)}. Utilizzando ad esempio le coordinate del punto {P_1}, abbiamo:

\small y-y_1=m(x-x_1) \quad \Rightarrow \quad y-1=2 \cdot(x-0) \quad \Rightarrow \quad y-1=2x

da cui in conclusione otteniamo l’equazione in forma esplicita:

y=2x+1

Esercizio 4

Scrivere l’equazione in forma implicita della retta del piano passante per i punti {P_1=\left( \dfrac{2}{3}, -4\right)} e {P_2= \left( \dfrac{1}{3}, \dfrac{1}{5}\right)}.

Coefficiente angolare:

m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{\frac{1}{5}-(-4)}{\frac{1}{3}-\frac{2}{3}}=\dfrac{21}{5} \cdot (-3)=-\dfrac{63}{5}

Utilizziamo a questo punto l’equazione {y-y_1=m(x-x_1)}:

y-(-4)=-\dfrac{63}{5}\left(x-\dfrac{2}{3}\right)

da cui:

y+4=-\dfrac{63}{5}x+\dfrac{42}{5}

e quindi, riscrivendo l’equazione in forma implicita:

\dfrac{63}{5}x+y+4-\dfrac{42}{5}=0

ovvero:

\dfrac{63}{5}x+y-\dfrac{22}{5}=0

Per esprimere nella forma più corretta l’equazione mettiamo tutti i termini a denominatore comune, in modo da poter poi ricondurci alla forma intera:

\dfrac{63x+5y-22}{\cancel{5}}=0 \quad \Rightarrow \quad 63x+5y-22=0

Abbiamo così terminato.

Terza parte: esercizi sulla retta passante per due punti con l’utilizzo della formula diretta (senza il calcolo di m)

Esercizio 5

Scrivere l’equazione in forma implicita della retta passante per i due punti {P_1=(x_1, y_1)=(2,3)} e {P_2=(x_2, y_2)=\left( \dfrac{1}{2}, 1\right)}.

Utilizziamo la formula:

\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_!}

Nel nostro caso, sostituendo le coordinate dei punti dati:

\dfrac{y-3}{1-3}=\dfrac{x-2}{\frac{1}{2}-2}

ovvero:

\dfrac{y-3}{-2}=\dfrac{x-2}{-\frac{3}{2}}

Aggiustiamo i segni:

\dfrac{3-y}{2}=\dfrac{2-x}{\frac{3}{2}}

Eseguiamo la divisione al secondo membro (questa può essere riscritta come un prodotto, ricordando di invertire numeratore e denominatore della frazione al divisore):

\dfrac{3-y}{2}=(2-x) \cdot \dfrac{2}{3}

Sviluppiamo i calcoli al secondo membro:

\dfrac{3-y}{2}=\dfrac{4}{3}-\dfrac{2}{3}x

Ora, portiamo tutto al primo membro:

\dfrac{3-y}{2}-\dfrac{4}{3}+\dfrac{2}{3}x=0

Mettiamo tutto a denominatore comune:

\dfrac{9-3y-8+4x}{6}=0

Eliminiamo direttamente il numeratore (è un numero) e riordiniamo i termini, ottenendo in conclusione l’equazione in forma implicita:

4x-3y+1=0

che è l’equazione della rette passante per i due punti dati.

Esercizio 6

Scrivere l’equazione in forma implicita della retta passante per i due punti {P_1=\left(1, -\dfrac{1}{4}\right)} e {P_2=\left( -4, \dfrac{9}{4}\right)}.

Procedendo in modo simile all’esercizio precedente, abbiamo:

\begin{align*} &\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}; \\ \\ & \dfrac{y-\left( -\frac{1}{4}\right)}{\frac{9}{4}-\left( -\frac{1}{4}\right)}=\dfrac{x-1}{-4-1}; \\ \\ & \dfrac{y+\frac{1}{4}}{\frac{9}{4}+\frac{1}{4}}=\dfrac{x-1}{-5}; \\ \\ &\dfrac{4y+1}{\cancel{4}^{\scriptsize \displaystyle 2}} \cdot \dfrac{\cancel{2}}{5} = \dfrac{1-x}{5}; \\ \\  & \dfrac{4y+1}{2}=1-x; \\ \\ &\dfrac{4y+1-2+2x}{\cancel{2}} =0; \\ \\  &2x+4y-1=0 \end{align*}

Terza parte: esercizi sulla retta passante per due punti calcolando m e q a partire dalle coordinate dei punti dati

Proseguiamo questa serie di esercizi sulla retta passante per due punti mostrando un metodo che si basa sull’utilizzo della formula ormai nota:

m=\dfrac{y_2-y_1}{x_2-x_1}

e della formula seguente, che consente di calcolare l’ordinata all’origine {q} a partire dalle coordinate di due punti {P_1=(x_1, y_1)} e {P_2=(x_2, y_2)} appartenenti alla retta:

q=\dfrac{x_1y_2-x_2y_1}{x_1-x_2}

Le due formule sono entrambe valide per punti non allineati verticalmente.

Esercizio 7

Scrivere l’equazione in forma esplicita della retta del piano passante per i punti {P_1=(x_1, y_1)=(1, -2)} e {P_2=(x_2,y_2)=(4,1)}.

Calcoliamo il coefficiente angolare {m} e l’ordinata all’origine {q} della retta in esame a partire dalle coordinate dei due punti dati:

\begin{align*} &m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{1-(-2)}{4-1}=1; \\ \\ & q=\dfrac{x_1y_2-x_2y_1}{x_1-x_2}=\dfrac{1 \cdot 1 - 4 \cdot (-2)}{1-4}=\dfrac{9}{-3}=-3\end{align*}

Così esprimendo l’equazione della retta in esame nella forma esplicita {y=mx+q} abbiamo in conclusione:

y=mx+q, \quad m=1, \: q=-3 \quad \Rightarrow \quad y=x-3

Esercizio 8

Scrivere l’equazione in forma implicita della retta del piano passante per i punti {P_1=(-3,-11)} e {P_2=(1,9)}.

Procedendo come nell’esercizio precedente, abbiamo:

\begin{align*} &m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{9-(-11)}{1-(-3)}=\dfrac{9+11}{1+3}=5; \\ \\ &q = \dfrac{x_1y_2-x_2y_1}{x_1-x_2}=\dfrac{-3 \cdot 9-1 \cdot (-11)}{-3-1}=\dfrac{-27+11}{-4}=\dfrac{-16}{-4}=4\end{align*}

Così l’equazione della retta passante per i due punti dati in forma esplicita è:

y=5x+4

Tuttavia il testo richiede di scrivere l’equazione della retta passante per i due punti nella forma implicita. Procediamo allora riconducendo alla forma implicita l’equazione appena scritta. Trasportiamo tutti i termini al primo membro, quindi ordiniamoli:

y-5x-4=0 \quad \Rightarrow \quad -5x+y-4=0

Per un discorso estetico, concludiamo cambiando il segno a tutti i termini:

5x-y+4=0

L’equazione è ora nella forma richiesta dal testo (forma implicita).

Oltre a tutti i metodi sin qui presentati, esiste per completezza un altro possibile metodo, che si basa sul calcolo dell’ordinata all’origine e quindi sull’utilizzo dell’equazione di una retta con coordinate di un punto e pendenza note.

Proviamo ad esempio a scrivere con quest’ultimo metodo l’equazione in forma esplicita della retta del piano passante per i punti {P_1=(2,3)} e {P_2=(4,5)}.

Cominciamo calcolando l’ordinata all’origine:

q=\dfrac{x_1y_2-x_2y_1}{x_1-x_2}=\dfrac{2 \cdot 5- 4 \cdot 3}{2-4}=\dfrac{10-12}{-2}=\dfrac{-2}{-2}=1

Ora sostituiamo il valore appena ottenuto per {q} e le coordinate ad esempio del punto {P_1} nell’equazione:

y-y_0=m(x-x_0)

Otteniamo:

y-3=1(x-2) 

Si ha:

y-3=x-2

da cui in conclusione:

y=x+1

Procedimento alternativo. Una volta calcolata l’ordinata all’origine, è anche possibile ricavare il coefficiente angolare m dall’equazione {y=mx+q}:

m=\dfrac{y_1-q}{x_1}=\dfrac{3-1}{2}=1

e quindi scrivere l’equazione cercata nella forma {y=mx+q}:

y=1 \cdot x + 1 \quad \Rightarrow  \quad y=x+1

Il metodo (in una o nell’altra variante) non presenta particolari vantaggi nell’utilizzo. Esso infatti richiede di ricordarsi la formula dell’ordinata all’origine espressa con le coordinate di due punti della retta (piuttosto scomoda), ed inoltre richiede di ragionare sull’equazione di una retta, in uno dei due modi mostrati. Meglio quindi utilizzare uno degli altri metodi presentati in precedenza. 😉

Rette verticali ed orizzontali

Per quanto riguarda questa serie di esercizi sulla retta passante per due punti non allineati né orizzontalmente, né verticalmente è tutto. Ricordiamo ancora una volta quanto già detto all’inizio della lezione: la scelta del metodo da utilizzare dovrà essere fatta sulla base delle indicazioni dell’insegnante e anche in base alle vostre attitudini. I primi due metodi presentati sono forse quelli più ragionati, mentre gli ultimi due metodi sono quelli più basati sul ricordarsi delle formule.

Prima di salutarci, vediamo un paio di esempi relativi al caso di esercizi sulla retta passante per due punti allineati orizzontalmente oppure verticalmente. In altre parole, intendiamo esaminare brevemente i casi di rette orizzontali e verticali.

Esercizio 9

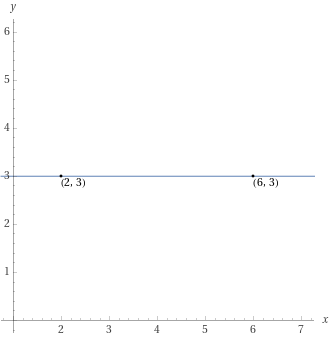
Scrivere l’equazione della retta passante per i due punti {P_1=(2,3)} e {P_2=(6,3)}.

Siamo nel caso di due punti allineati orizzontalmente. Infatti, i due punti hanno la stessa ordinata, uguale a {3}:

y_1=y_2 \quad \Rightarrow \quad \text{punti allineati orizzontalmente}

Di conseguenza, la retta passante per i due punti sarà necessariamente orizzontale, ed avrà equazione:

y=3

ove al secondo membro figura l’ordinata comune ai due punti.

Esercizio 10

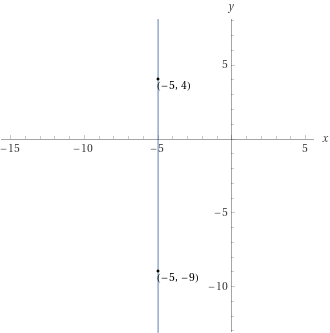
Scrivere l’equazione della retta passante per i due punti {P_1=(-5,4)} e {P_2=(-5,-9)}.

I due punti sono in questo caso allineati verticalmente. Infatti, questi condividono la stessa ascissa {-5}:

x_1=x_2 \quad \Rightarrow \quad \text{punti allineati verticalmente}

Così, la retta in esame sarà necessariamente verticale, e la sua equazione è:

x=-5

ove al secondo membro abbiamo l’ascissa in comune ai due punti dati.

Ora è veramente tutto! Buon proseguimento con SìMatematica, un saluto a tutti voi! 🙂