Equazione della circonferenza

 - 

Circonferenza (scuole superiori)

L’equazione della circonferenza è esprimibile utilizzando due forme: l’equazione della circonferenza con centro e raggio, che in generale si scrive (x – x_C)²+(y – y_C)²=r², e l’equazione della circonferenza in forma canonica, la quale invece è esprimibile come x² + y² + ax + by + c = 0.

In questa lezione ci occuperemo quindi di aspetti già anticipati nella prima lezione sulla circonferenza, ma con un taglio più ampio e fornendo maggiori esercizi di esempio.

Come vedremo, l’equazione della circonferenza con centro e raggio discende direttamente dalla definizione di circonferenza come luogo geometrico, mentre l’equazione in forma canonica si ottiene sviluppando i prodotti al primo membro dell’equazione con centro e raggio, operando poi delle opportune sostituzioni. Nella pratica, si preferisce per comodità e maggiore rapidità di calcolo utilizzare delle formule specifiche, che comunque discendono dalle sostituzioni operate.

Mostreremo in particolare come passare dall’equazione con centro e raggio di una circonferenza alla corrispondente equazione in forma canonica. Vedremo inoltre come ricavare centro e raggio della circonferenza anche a partire dall’equazione in forma canonica, e mostreremo la condizione grazie alla quale è possibile all’occorrenza verificare se un’equazione rappresenta o meno una circonferenza (intesa come reale non degenere).

Per chi non desidera ricordare le formule, illustreremo infine come ricavare centro e raggio di una circonferenza a partire dalla sua equazione in forma canonica, utilizzando il metodo del completamento dei quadrati.

Infine, vedremo come cavarcela anche in quei casi ove l’equazione della circonferenza non si presenta propriamente in nessuna delle due forme con centro e raggio e canonica. Come vedremo, si tratterà nella maggior parte dei casi di dividere tutti i termini presenti nell’equazione per un’opportuna quantità.

Cominciamo allora subito a vedere come scrivere l’equazione della circonferenza del piano cartesiano, utilizzando le varie forme possibili, svolgendo insieme degli esercizi di esempio.

Equazione della circonferenza con centro e raggio

Sia data una circonferenza con centro {C=(x_C, y_C)} e raggio {r}. La circonferenza è una particolare curva piana, ed in particolare può essere vista come il luogo di punti (insieme di punti) tali da essere tutti equidistanti dal centro della circonferenza stessa. Il raggio è proprio la comune distanza che ha ogni punto della circonferenza rispetto al centro della figura.

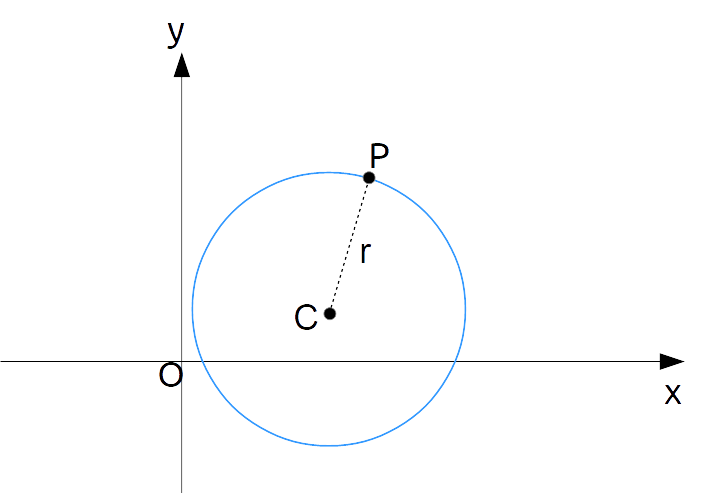
Così, fra tutti i punti del piano cartesiano, che indicheremo con {\pi}, i punti {P} appartenenti alla circonferenza di raggio {r} e centro {C} saranno tali da rispettare la seguente condizione:

|CP|=r

Con ciò intendiamo che ciascun punto della circonferenza dovrà essere distante dal centro della circonferenza stessa di una distanza uguale al raggio {r}. E, fatto molto importante, la quantità {r} è fissata.

Osserviamo che utilizzando tale condizione possiamo scrivere la rappresentazione formale di una circonferenza intesa come luogo geometrico di punti (insieme di punti):

\mathscr{C}=\left\{ P \in \pi \: | \: \overline{CP}=r\right\}

Con tale scrittura intendiamo che la circonferenza di centro {C} e raggio {r} è l’insieme dei punti del piano cartesiano {\pi} tali da avere una distanza rispetto al centro {C} della circonferenza uguale a {r}.

Ora, la rappresentazione appena scritta consente di ottenere, se opportunamente riletta, un’equazione algebrica in grado di rappresentare la circonferenza. In particolare, dobbiamo soffermarci sulla condizione:

\overline{CP} = r

Al primo membro abbiamo la distanza tra i due punti {C} e {P}. Così, indicando con {x_C} e {y_C} le coordinate del centro {C} della circonferenza, utilizzando la formula della distanza tra due punti del piano è possibile riesprimere in altra forma il primo membro della precedente uguaglianza, ottenendo l’equazione:

\underbrace{\sqrt{(x-x_C)^2+(y-y_C)^2}}_{\overline{CP}}=r

Ora, l’equazione appena scritta è irrazionale, in quanto il primo membro ha le incognite sotto radice. Tuttavia, in questo caso pur avendo un radicale con indice pari, non servono le discussioni in genere necessarie per le equazioni irrazionali.

Per rendersene conto, basta osservare due fatti. In primo luogo, la quantità al primo membro, essendo una radice quadrata, è sempre positiva. Inoltre, anche la quantità al secondo membro è sempre positiva, poiché è una misura geometrica (in questo caso, un raggio). Così, non dobbiamo imporre alcuna condizione di concordanza dei segni.

In più, la quantità all’interno della radice al primo membro è una somma di quadrati, quindi sempre positiva. Di conseguenza, non dobbiamo nemmeno imporre una condizione di realtà del radicale al primo membro.

Per tutto quanto detto, è possibile elevare al quadrato entrambi i membri dell’equazione, senza alcuna discussione:

\small \left[\sqrt{(x-x_C)^2+(y-y_C)^2}\right]^2=r \quad \Rightarrow \quad(x-x_C)^2+(y-y_C)^2=r^2

Quella appena ottenuta è l’equazione con centro e raggio della circonferenza. Infatti, compaiono esplicitamente le coordinate {x_C} ed {y_C} del centro della circonferenza, e il raggio {r} della circonferenza stessa, elevato al quadrato. Con un po’ di attenzione ai segni è dunque immediato ricavare le coordinate del centro da tale equazione. Infine, è pure immediato ricavare il raggio, poiché basta soltanto estrarre la radice quadrata del secondo membro dell’equazione, ovvero della quantità {r^2}.

L’equazione con centro e raggio di una circonferenza si esprime come{(x-x_C)^2+(y-y_C)^2=r^2}ove {x_C} ed {y_C} sono rispettivamente l’ascissa e l’ordinata del centro {C} della circonferenza, mentre {r} è la misura del suo raggio.

Così, tutti i punti che appartengono alla circonferenza sono tali da soddisfare tale equazione. Di conseguenza, per testare se un dato punto del piano appartiene o meno ad una fissata circonferenza, basta sostituire le coordinate del punto nell’equazione della circonferenza stessa, e quindi verificare che si ottiene un’uguaglianza numerica vera. In tal caso il punto appartiene alla circonferenza. Diversamente, se si ottiene un’uguaglianza numerica falsa, il punto non appartiene alla circonferenza.

Diciamo quindi che la condizione di appartenenza di un punto ad una circonferenza richiede che le coordinate di tale punto, sostituite nell’equazione della circonferenza, diano un’uguaglianza numerica vera.

Vediamo ora degli esempi relativi all’equazione della circonferenza con centro e raggio.

Esempio 1

Scrivere l’equazione della circonferenza del piano cartesiano avente centro {C=(2,5)} e raggio {r=7}.

Se il centro della circonferenza è {C=(2,5)}, allora le coordinate del centro della figura sono {x_C=2} e {y_C=5}. Inoltre, abbiamo {r=7}. Di conseguenza, l’equazione con centro e raggio:

(x-x_C)^2+(y-y_C)^2=r^2

nel nostro caso diviene, sostituendo i valori:

(x-2)^2+(y-5)^2=7^2

ovvero in conclusione:

(x-2)^2+(y-5)^2=49

E questa è l’equazione con centro e raggio della circonferenza data.

Esempio 2

Scrivere l’equazione della circonferenza con centro {C=(-3,9)} e raggio {r=4}.

Poiché è {C=(-3,9)}, le coordinate del centro della circonferenza sono {x_C=-3} e {y_C=9}. Il raggio è {r=4}.

In questo caso occorre prestare particolare attenzione al fatto che una delle coordinate del centro è negativa. Abbiamo infatti {x_C=-3}. Al fine di evitare spiacevoli errori di segno, conviene sostituire i valori delle coordinate del centro nell’equazione facendo abbondante uso delle parentesi:

[x-(-3)]^2+(y-9)^2=4^2

e quindi, utilizzando le regole sui segni note dall’algebra elementare:

(x+3)^2+(y-9)^2=16

Abbiamo in questo modo ottenuto anche in questo caso l’equazione con centro e raggio della circonferenza in esame.

Esempio 3

Ricavare i valori delle coordinate del centro e del raggio della circonferenza di equazione {(x-3)^2+(y-5)^2=36}.

Confrontiamo l’equazione data con l’equazione di una generica circonferenza con centro e raggio:

(x-x_C)^2+(y-y_C)^2=r^2

In particolare abbiamo nel nostro caso:

(x-\underbrace{3}_{x_C})^2+(y-\underbrace{5}_{y_C})^2=\underbrace{36}_{r^2}

Quindi dal confronto tra le due equazioni segue immediatamente:

x_C=3, \qquad y_C=5, \qquad r^2=36

Di conseguenza il centro della circonferenza in esame è:

C=(3,5)

mentre per il raggio abbiamo in conclusione:

r=\sqrt{r^2}=\sqrt{36}=6

Tra parentesi, osserviamo che si ha {\sqrt{r^2}=r} e non {|r|}, poiché il raggio, essendo una distanza, è una quantità sempre positiva.

Esempio 4

Ricavare i valori delle coordinate del centro e del raggio della circonferenza di equazione {(x-9)^2+(y+2)^2=25}.

Qui occorre prestare molta attenzione. Guardiamo con attenzione all’equazione data:

(x-9)^2+(y \:\boxed{+} \:2)^2=25

Come evidenziato, i termini del secondo quadrato al primo membro sono separati tra loro da un segno più, e non da un segno meno come nell’equazione di una circonferenza con centro e raggio nella sua forma generale. Così, per evitare errori di segno dobbiamo anzitutto riscrivere l’equazione data nel nostro caso di modo da avere una differenza anche nel secondo quadrato al primo membro. Per il primo quadrato invece non abbiamo problemi, poiché i termini sono già separati da un segno meno (abbiamo infatti la quantità {x-9}).

Perciò, occorre riscrivere l’equazione data come segue:

(x-9)^2+[y-(-2)]^2=25

infatti {y-(-2)=y+2}.

In questo modo è possibile individuare correttamente le coordinate {x_C} ed {y_C} del centro della circonferenza:

(x-\underbrace{9}_{x_C})^2+[y-(\underbrace{-2}_{y_C})]^2=25

da cui segue:

C=(9, -2)

Possiamo infine calcolare il raggio, che come nell’esempio precedente è dato dalla radice quadrata del secondo membro:

r=\sqrt{25}=5

Esempio 5

Verificare se i punti {A=(-2,4)} e {B=(7,3)} appartengono alla circonferenza di equazione con centro e raggio {(x-2)^2+(y-3)^2=25}.

Per verificare se un punto appartiene ad una circonferenza, dobbiamo testare per esso la condizione di appartenenza alla circonferenza stessa. Così, dobbiamo vedere se le coordinate del punto in esame soddisfano l’equazione della circonferenza data, ovvero se sostituendo i valori di tali coordinate otteniamo un’uguaglianza numerica vera. In tal caso, il punto appartiene alla circonferenza.

Cominciamo a testare il punto {A=(-2,4)}. Sostituiamo alle incognite {x} ed {y} nell’equazione della circonferenza i valori delle sue coordinate. Stiamo particolarmente attenti a sostituire all’incognita {x} l’ascissa del punto {A}, ovvero {-2}, ed all’incognita {y} l’ordinata del punto {A}, ovvero {4}.

\begin{align*} &(x-2)^2+(y-3)^2=25 \quad \text{con} \quad x=-2, \: y =4 \quad (\text{punto} \: A) \\ \\ & \Rightarrow (-2-2)^2+(4-3)^2=25 \quad \Rightarrow \quad (-4)^2+1^2=25 \quad \Rightarrow \: 17=25 \quad \text{falso}\end{align*}

Quindi il punto {A} non appartiene alla circonferenza poiché sostituendo le sue coordinate nell’equazione della circonferenza abbiamo ottenuto un’uguaglianza numerica falsa.

Passiamo ora al punto {B=(7,3)}. Sostituiamo le sue coordinate nell’equazione della circonferenza data:

\begin{align*} &(x-2)^2+(y-3)^2=25 \quad \text{con} \quad x=7, \: y =3 \quad (\text{punto} \: B) \\ \\ & \Rightarrow (7-2)^2+(3-3)^2=25 \quad \Rightarrow \quad (5)^2+0=25 \quad \Rightarrow \: 25=25 \quad \text{vero}\end{align*}

In questo caso otteniamo un’uguaglianza numerica vera e quindi il punto {B} appartiene alla circonferenza.

Ora, analizziamo brevemente un paio di casi particolari.

Circonferenza con centro nell’origine degli assi

Se la circonferenza ha come centro l’origine, basta porre {x_C=0} ed {y_C=0} (l’ascissa e l’ordinata dell’origine sono entrambe nulle). In tal caso l’equazione con centro e raggio della circonferenza diviene:

(x-0)^2+(y-0)^2=r^2

e quindi:

x^2+y^2=r^2 \qquad \text{circonferenza centrata nell'origine}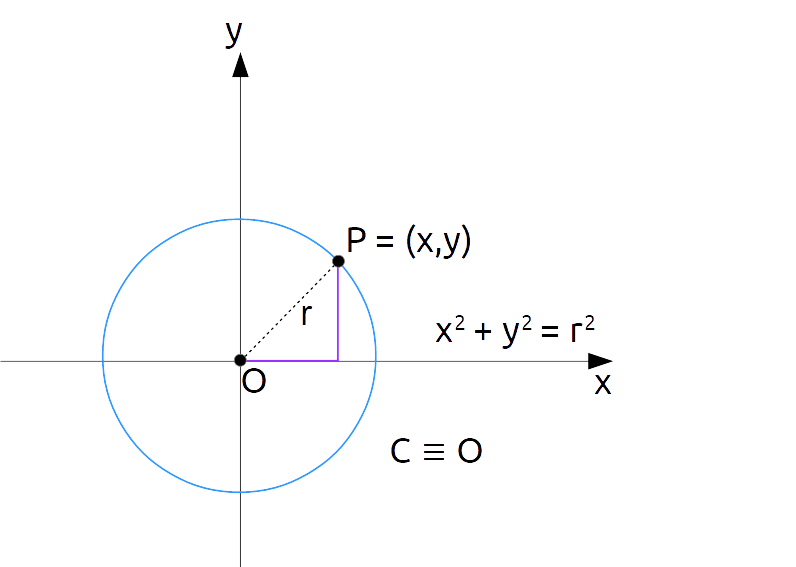

L’equazione {x^2+y^2=r^2} si può ottenere come diretta applicazione del teorema di Pitagora. Infatti, è possibile individuare in figura un triangolo rettangolo con ipotenusa di misura {r} e con cateti di misure rispettivamente {x} ed {y}.

Circonferenza passante per l’origine

Se una circonferenza è passante per l’origine, le coordinate dell’origine (entrambe nulle) devono soddisfare la condizione di appartenenza alla circonferenza. In altre parole, sostituendo nell’equazione della circonferenza {x=0} ed {y=0} dovremo ottenere un’uguaglianza numerica vera.

Consideriamo la generica circonferenza con equazione espressa nella forma con centro e raggio:

(x-x_C)^2+(y-y_C)^2=r^2

Supponiamo che tale circonferenza sia passante per l’origine. Sostituendo le coordinate dell’origine ad {x} ed {y} otteniamo:

(0-x_C)^2+(0-y_C)^2=r^2

da cui si ha:

x_C^2+y_C^2=r^2

Se tale uguaglianza risulta vera, la circonferenza è passante per l’origine.

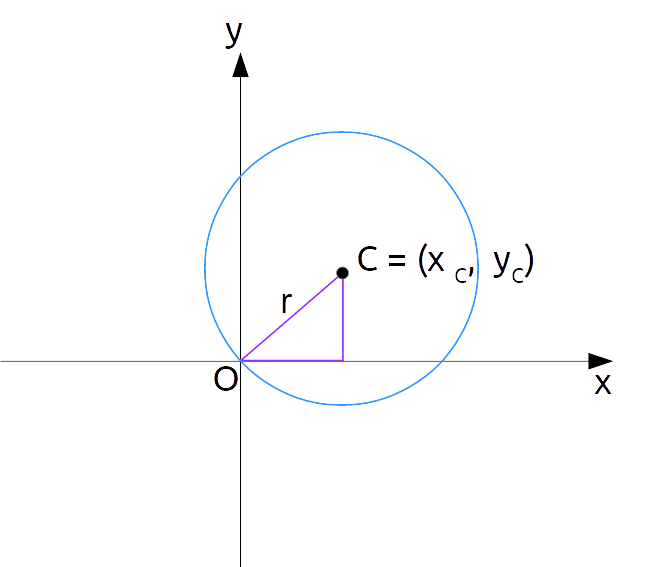
Inoltre, da tale uguaglianza si deduce che:

r=\sqrt{x_C^2+y_C^2} \qquad \text{solo per circonferenza passante per l'origine}

Quindi, una circonferenza che passa per l’origine ha raggio esprimibile come la radice della somma dei quadrati dei valori delle coordinate del centro della circonferenza stessa. Ciò è anche una conseguenza del teorema di Pitagora, come mostra la precedente figura.

Come vedremo fra poco, tale espressione per il raggio non è valida per una circonferenza che non passa per l’origine. Perciò, attenzione. 😉

Equazione della circonferenza in forma canonica

Riprendiamo l’equazione della circonferenza nella forma con centro e raggio:

(x-x_C)^2+(y-y_C)^2=r^2

Proviamo a sviluppare i quadrati di binomi al primo membro:

x^2-2x_Cx+x_C^2+y^2-2y_Cy+y_C^2=r^2

A questo punto, riordiniamo i termini come segue:

x^2+y^2-2x_Cx-2y_Cy+x_C^2+y_C^2=r^2

Trasportiamo infine il termine {r^2} al primo membro:

x^2+y^2-2x_Cx-2y_Cy+x_C^2+y_C^2-r^2=0

A questo punto poniamo per comodità le sostituzioni:

-2x_C=a, \quad -2y_C=b, \quad x_C^2+y_C^2-r^2=c

La precedente equazione allora diviene:

x^2+y^2+ax+by+c=0

e questa è sotto opportune ipotesi l’equazione in forma canonica della circonferenza. Come possiamo vedere, tale equazione somiglia all’equazione in forma implicita di una retta {ax+by+c=0}. Infatti, abbiamo il secondo membro nullo, ed al primo membro figurano soltanto somme algebriche tra termini, senza prodotti da calcolare. Tra l’altro, le due equazioni hanno dei termini in comune, ma nell’equazione in forma canonica della circonferenza abbiamo in più i termini di secondo grado {x^2} ed {y^2}.

L’equazione in forma canonica della circonferenza si scrive come {x^2+y^2+ax+by+c=0, \qquad a,b,c \in \R}Tale equazione rappresenta una circonferenza (reale non degenere) se e solo se vale la condizione {\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0}

Precisiamo che per circonferenza “reale non degenere” intendiamo una circonferenza con raggio reale positivo non nullo. In altre parole, il raggio dovrà essere un numero reale e tale da soddisfare la condizione {r > 0}.

Ora, la condizione posta sui coefficienti {a,b,c}, ovvero la condizione {\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0}, discende dal fatto che per scrivere l’equazione canonica abbiamo operato la sostituzione:

 x_C^2+y_C^2-r^2=c

da cui segue:

r^2=x_C^2+y_C^2-c \quad \Rightarrow \quad r=\sqrt{x_C^2+y_C^2-c}

Ora, attenzione. Il raggio viene espresso come una quantità sotto radice quadrata (indice pari). Quindi, affinché l’espressione così ottenuta per {r} abbia significato, la quantità all’interno della radice deve essere non negativa. Inoltre, richiediamo che il raggio sia diverso da zero per non avere una circonferenza di raggio nullo (circonferenza degenere). Diversamente, una circonferenza con raggio nullo si ridurrebbe ad un punto.

Così, dovrà essere per detti motivi:

x_C^2+y_C^2-c > 0

Ora, poiché per scrivere l’equazione in forma canonica della circonferenza abbiamo anche posto le sostituzioni:

-2x_C=a, \quad -2y_C=b

da esse otteniamo rispettivamente:

x_C=-\dfrac{1}{2}a, \qquad y_C=-\dfrac{1}{2}b

Per cui tenendo conto di tali uguaglianze, la condizione {x_C^2+y_C^2-c > 0} diviene:

\left( -\dfrac{1}{2}a\right)^2+\left( -\dfrac{1}{2}b\right)^2-c > 0

ovvero:

\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0

che è la condizione che figura nella definizione dell’equazione canonica di una circonferenza.

Passaggio dall’equazione con centro e raggio all’equazione canonica della circonferenza

L’obiettivo che ora ci poniamo è quello di scrivere l’equazione in forma canonica di una data circonferenza a partire dalla sua equazione con centro e raggio:

(x-x_C)^2+(y-y_C)^2=r^2

La prima osservazione da fare è che per scrivere la corrispondente equazione in forma canonica, dobbiamo ricavare i coefficienti {a,b,c} corrispondenti alle coordinate {x_C} ed {y_C} del centro ed al raggio {r}. Per fare questo, ci vengono in aiuto le sostituzioni che abbiamo operato per scrivere l’equazione in forma canonica della circonferenza, ovvero:

-2x_C=a, \quad -2y_C=b, \quad x_C^2+y_C^2-r^2=c

Se le rileggiamo in senso inverso, otteniamo:

a=-2x_C, \quad b=-2y_C, \quad c=x_C^2+y_C^2-r^2 \qquad (*)

Di conseguenza, a partire dai valori delle coordinate del centro e dal raggio, direttamente ricavabili dall’equazione della circonferenza con centro e raggio, possiamo calcolare i coefficienti {a,b,c} che consentono di scrivere l’equazione di quella stessa circonferenza in forma canonica.

Osserviamo che le espressioni attribuite ai coefficienti {a,b,c} nelle * hanno senso in tutto l’insieme dei numeri reali. Di conseguenza, è sempre possibile riscrivere in forma canonica l’equazione con centro e raggio di una circonferenza assegnata.

Ma vediamo subito un esempio su come passare dall’equazione con centro e raggio all’equazione in forma canonica di una circonferenza.

Esempio 6

Scrivere l’equazione in forma canonica della seguente circonferenza, con equazione inizialmente data nella forma con centro e raggio:{(x-5)^2+(y+1)^2=9}

Poiché le * utilizzano le coordinate del centro e la misura del raggio, dobbiamo prima di tutto ricavare tali valori a partire dall’equazione data:

(x-5)^2+(y+1)^2=9 \quad \Rightarrow \quad x_C=5, \: y_C=-1, \: r=\sqrt{9}=3

Ora sfruttando le * possiamo ricavare i coefficienti {a,b,c} necessari per scrivere l’equazione in forma canonica:

\begin{align*} & a=-2x_C=-2  \cdot 5 = -10, \quad b=-2y_C=-2 \cdot (-1)=2, \\ \\ & c={x_C^2+y_C^2-r^2} =5^2+(-1)^2-3^2=25+1-9=17\end{align*}

Ora non resta che sostituire i valori appena calcolati relativi ai coefficienti {a,b,c} nell’equazione in forma canonica di una generica circonferenza:

x^2+y^2+ax+by+c=0

ottenendo in conclusione l’equazione in forma canonica della circonferenza in esame:

x^2+y^2+(-10)x+2y+17=0

ovvero:

x^2+y^2-10x+2y+17=0

Passaggio dall’equazione in forma canonica della circonferenza a quella con centro e raggio

Vediamo ora il problema inverso al precedente, ovvero come scrivere l’equazione con centro e raggio di una circonferenza a partire dall’equazione in forma canonica. Risolvendo tale problema, vedremo di conseguenza anche come trovare le coordinate del centro e il raggio a partire dall’equazione canonica di una circonferenza.

Prima di tutto, osserviamo ancora che non sempre l’equazione

x^2+y^2+ax+by+c=0, \qquad a,b,c \in \R

rappresenta una circonferenza reale non degenere. Come abbiamo visto, affinché ciò avvenga deve infatti valere la condizione:

\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0

Sotto tale condizione, l’equazione effettivamente rappresenta una circonferenza (reale non degenere) ed è possibile determinarne le coordinate del centro e del raggio.

Ora, riscriviamo per comodità le *:

a=-2x_C, \quad b=-2y_C, \quad c=x_C^2+y_C^2-r^2 \qquad (*)

Esplicitando le coordinate del centro ed il raggio otteniamo le relazioni:

x_C=-\dfrac{1}{2}a, \quad y_C=-\dfrac{1}{2}b, \quad r^2=\sqrt{x_C^2+y_C^2-c} \qquad (**)

grazie alle quali possiamo ricavare le coordinate del centro ed il raggio della circonferenza, necessari per scrivere l’equazione con centro e raggio della circonferenza stessa.

Basterà a questo punto sostituire i valori ottenuti nell’equazione con centro e raggio di una generica circonferenza:

(x-x_C)^2+(y-y_C)^2=r^2

ottenendo in conclusione l’equazione con centro e raggio della circonferenza data.

Esempio 7

Ricavare centro e raggio e scrivere l’equazione nella forma con centro e raggio della circonferenza avente la seguente equazione in forma canonica:{x^2+y^2+3x+4y-27=0}

Anzitutto per completezza verifichiamo che all’equazione {x^2+y^2+3x+4y-27=0} corrisponda effettivamente una circonferenza reale non degenere. Confrontando l’equazione data con l’equazione canonica di una circonferenza generica, ovvero {x^2+y^2+ax+by+c=0}, otteniamo confrontando tra loro i coefficienti delle due equazioni:

a=3, \: b=4, \: c=-27

Importante. Attenzione a non compiere errori di segno. Può essere utile allo scopo riscrivere l’equazione data, ovvero in questo caso l’equazione {x^2+y^2+3x+4y-27=0}, come {x^2+y^2+3x+4y+(-27)=0}. In tal modo riesce evidente che il termine {c} è uguale a {-27} e non a {27}.

Di conseguenza, la condizione per avere una circonferenza reale non degenere è:

\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0 \quad \Rightarrow \quad \dfrac{3^2}{4}+\dfrac{4^2}{4}-(-27)> 0 \quad \Rightarrow \: \dfrac{133}{4}>0 \quad \text{OK}

La circonferenza è reale non degenere e quindi ha senso calcolarne le coordinate del centro ed il raggio.

Utilizzando in particolare le ** otteniamo, a partire dai coefficienti {a,b,c}:

\begin{align*} &x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot 3 = -\dfrac{3}{2};\\ \\ & y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot 4=-2; \\ \\ & r=\sqrt{x_C^2+y_C^2-c}=\sqrt{\left( -\dfrac{3}{2}\right)^2+\left( -2\right)^2-(-27)}=\\ \\ & =\sqrt{\dfrac{9}{4}+4+27}=\sqrt{\dfrac{9+16+108}{4}}=\sqrt{\dfrac{133}{4}}= \dfrac{\sqrt{133}}{2}\end{align*}

Così la circonferenza data ha centro {C=\left( -\dfrac{3}{2}, -2\right)} e raggio {\dfrac{\sqrt{133}}{2}}.

Disponendo ora di tali valori è immediato scrivere l’equazione con centro e raggio della circonferenza in esame:

\begin{align*} &(x-x_C)^2+(y-y_C)^2=r^2 \quad \text{con} \quad x_C=-\dfrac{3}{2}, \: y_C=-2, \: r=\dfrac{\sqrt{133}}{2} \\ \\ & \Rightarrow \left[ x-\left( -\dfrac{3}{2}\right)\right]^2+[y-(-2)]^2=\left( \dfrac{\sqrt{133}}{2}\right)^2;\\ \\ & \Rightarrow \left( x+\dfrac{3}{2}\right)^2+(y+2)^2=\dfrac{133}{4}\end{align*}

Siamo così riusciti a passare dalla equazione in forma canonica della circonferenza in esame all’equazione corrispondente con centro e raggio. Abbiamo così visto analizzando un caso pratico come passare dall’equazione in forma canonica di una circonferenza all’equazione con centro e raggio.

Metodo del completamento dei quadrati

Un procedimento alternativo per ricavare centro e raggio di una circonferenza a partire dalla sua equazione in forma canonica è dato dal metodo del completamento dei quadrati. Tale metodo è più macchinoso rispetto all’utilizzo delle formule illustrate in precedenza, tuttavia presenta l’evidente vantaggio di non dover ricordare tali formule a memoria o comunque dover ricavarle.

A partire dall’equazione canonica di una circonferenza:

x^2+y^2+ax+by+c=0

l’idea è quella di portare il termine noto al secondo membro:

x^2+y^2+ax+by=-c

e quindi cercare di riesprimere il polinomio al primo membro come una somma di quadrati. Allo scopo, prima di tutto occorre riordinare i termini al primo membro, scrivendo i termini nella stessa incognita uno di seguito all’altro:

x^2+ax+y^2+by=-c

Quindi, dobbiamo fare caso al fatto che le quantità {x^2+ax} e {y^2+by} sono dei quadrati di un binomio incompleti. Infatti, nella quantità {x^2+ax} ad esempio il termine {x^2} può essere visto come il quadrato di un termine, mentre {ax} può essere visto come un doppio prodotto. Stesso discorso vale per la quantità {y^2+by}.

Si tratterà quindi di sommare dei termini al primo membro in modo da completare i quadrati di un binomio, e sommare quegli stessi termini anche al secondo membro, in modo da rispettare il primo principio di equivalenza delle equazioni:

\underbrace{x^2+ax+\square }_{\substack{\text{primo quadrato}\\ \text{di un binomio}}}+\underbrace{y^2+by+\triangle}_{\substack{\text{secondo quadrato}\\ \text{di un binomio}}} =-c+ \square + \triangle

Per il momento abbiamo rappresentato schematicamente le quantità necessarie a completare i quadrati con delle figure geometriche. Nell’esempio a seguire chiariremo come determinare dette quantità.

Infine, una volta scritta l’equazione in tale forma, basterà riesprimere i quadrati dei binomi nella forma {(x+\dots})^2. In questo modo avremo ricondotto l’equazione canonica di partenza alla forma con centro e raggio. E sarà quindi immediato determinare le coordinate del centro e la misura del raggio della circonferenza in esame.

Esempio 8 (metodo del completamento dei quadrati)

Riscrivere nella forma con centro e raggio la seguente equazione in forma canonica di una circonferenza (reale non degenere):{x^2+y^2+3x+4y-27=0}

Il testo già ci dice che la circonferenza è reale non degenere, per cui non dobbiamo eseguire la verifica.

Ci ritroviamo ancora di fronte all’equazione dell’esempio 7. Vediamo se applicando il metodo del completamento dei quadrati perveniamo correttamente agli stessi risultati.

Data l’equazione in forma canonica di partenza:

x^2+y^2+3x+4y-27=0

cominciamo trasportando il termine noto al secondo membro:

x^2+y^2+3x+4y=27

Ora, riordiniamo i termini al primo membro come indicato in precedenza:

x^2+3x+y^2+4y=27

I quadrati di binomi da completare sono {x^2+3x} e {y^2+4y}.

Cominciamo completando {x^2+3x}. Il doppio prodotto è dato dal termine {3x} (l’unico dei due termini di primo grado, quindi la scelta è immediata). Abbiamo:

3x=2 \cdot \boxed{\dfrac{3}{2}} \cdot x

Così nel doppio prodotto figura il termine {\dfrac{3}{2}}, ed il suo quadrato è la quantità necessaria per il completamento. Infatti, il doppio prodotto contiene i fattori {\dfrac{3}{2}} e {x}, che sono i termini che compongono il binomio. Per cui per completare il quadrato di un binomio dovremo aggiungere alla quantità {x^2+3x} il quadrato di {\dfrac{3}{2}}, ovvero {\dfrac{9}{4}}. Così per l’equazione abbiamo intanto:

x^2+3x+\boxed{\dfrac{9}{4}}+y^2+4y=27+\boxed{\dfrac{9}{4}}

Osserviamo che abbiamo sommato la quantità {\dfrac{9}{4}} anche al secondo membro, in modo da rispettare il primo principio di equivalenza delle equazioni. Soltanto in questo modo completando i quadrati otterremo un’equazione equivalente a quella data. Quindi, attenzione! 😉

Ora rimane da completare il quadrato {y^2+4y}. Ancora, analizziamo il termine {4y}, che evidentemente rappresenta il doppio prodotto:

4y=2 \cdot 2 \cdot y

Tra i fattori figura la quantità {2}, il cui quadrato, ovvero {4}, è il termine necessario per completare il quadrato. Per cui tornando all’equazione abbiamo:

\underbrace{x^2+3x+\boxed{\dfrac{9}{4}}}_{\substack{\text{primo quadrato} \\ \text{di un binomio}}}+\underbrace{y^2+4y+\boxed{4}}_{\substack{\text{secondo quadrato} \\ \text{di un binomio}}}=27+\boxed{\dfrac{9}{4}}+\boxed{4}

Lo ripetiamo ancora. Non dimentichiamo di sommare la quantità necessaria a completare il quadrato anche al secondo membro.

Ora non resta che riscrivere entrambi i quadrati di binomi rispettivamente nella forma {(x + \dots})^2 e {(y+ \dots)^2} . Abbiamo:

\left( x+\dfrac{3}{2}\right)^2+(y+2)^2=27+\dfrac{9}{4}+4

Infine sommiamo tra loro i termini al secondo membro:

\left( x+\dfrac{3}{2}\right)^2+(y+2)^2=\dfrac{133}{4}

A questo punto abbiamo ottenuto l’equazione con centro e raggio della circonferenza, a partire dall’equazione canonica di partenza. Onde evitare spiacevoli errori di segno, riscriviamo l’equazione come segue:

\left[ x-\underbrace{\left(-\dfrac{3}{2}\right)}_{x_C}\right]^2+[y-\underbrace{(-2)}_{y_C}]^2=\underbrace{\dfrac{133}{4}}_{r^2}

In conclusione abbiamo:

C=\left( -\dfrac{3}{2}, -2\right), \qquad r=\dfrac{\sqrt{133}}{2}

ritrovando così correttamente gli stessi risultati dell’esempio 7.

Equazione di una circonferenza nella forma Ax²+Ay²+Bx+Cy+D=0

Talvolta può capitare di ritrovarsi di fronte ad un’equazione di una circonferenza della forma:

Ax^2+Ay+Bx+Cy+D=0

con {A \neq 1} e non nullo.

Questa forma non è la forma canonica sin qui vista. Infatti, nell’equazione di una circonferenza in forma canonica i coefficienti {A} sono uguali ad {1}.

Prima di procedere alla determinazione del centro e del raggio della circonferenza, davanti ad un’equazione del genere è fondamentale ricordarsi di dividere tutti i termini presenti nell’equazione per {A}. In tal modo è possibile ricondursi alla forma canonica e quindi procedere al calcolo delle coordinate del centro e della misura del raggio della circonferenza in esame.

Se ad esempio è data l’equazione:

4x^2+4y^2+2x-3y-9=0

poiché i coefficienti dei termini in {x^2} e {y^2} sono diversi da 1, dobbiamo prima di tutto dividere tutti i termini dell’equazione per il comune coefficiente dei termini in {x^2} e {y^2}, ovvero {4}:

\dfrac{4}{4}x^2+\dfrac{4}{4}y^2+\dfrac{2}{4}x-\dfrac{3}{4}y-\dfrac{9}{4}=0

da cui:

x^2+y^2+\dfrac{1}{2}x-\dfrac{3}{4}y-\dfrac{9}{4}=0

Attenzione. Nell’equazione {Ax^2+Ay^2+By+Cy+D=0}, con {A} diverso da {1} e non nullo, i termini {B,C,D} non sono i termini a,b,c dell’equazione canonica della circonferenza! Così, per poter determinare i coefficienti {a,b,c} da una tale equazione dobbiamo prima dividere tutti i termini dell’equazione data per {A}.

Ora abbiamo ricondotto l’equazione di partenza alla forma canonica ed è possibile verificare se abbiamo una circonferenza reale non degenere oppure no, e quindi eventualmente calcolare centro e raggio della circonferenza con i metodi sin qui visti.

Nel caso in esame, abbiamo:

\dfrac{a^2}{4}+\dfrac{b^2}{4}-c=\dfrac{\left( \dfrac{1}{2}\right)^2}{4}+\dfrac{\left( -\dfrac{3}{4}\right)^2}{4}-\left( -\dfrac{9}{4}\right)=\dfrac{1}{16}+\dfrac{9}{64}+\dfrac{9}{4}> 0 \quad \text{OK}

quindi la circonferenza è reale e non degenere.

Infine, per le coordinate del centro e la misura del raggio:

\begin{align*} &x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot \dfrac{1}{2}=-\dfrac{1}{4}; \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2}\cdot \left( -\dfrac{3}{4}\right)=\dfrac{3}{8}; \\ \\ & r=\sqrt{x_C^2+y_C^2-c}=\sqrt{\left( -\dfrac{1}{4}\right)^2+\left( \dfrac{3}{8}\right)^2-\left( -\dfrac{9}{4}\right)}=\\ \\ & =\sqrt{\dfrac{1}{16}+\dfrac{9}{64}+\dfrac{9}{4}}=\sqrt{\dfrac{4+9+144}{64}}=\dfrac{\sqrt{157}}{8}\end{align*}

Nel caso in cui si utilizzi il metodo del completamento dei quadrati, di fronte ad un’equazione con coefficiente dei termini in {x^2} e {y^2} diverso da {1}, non è obbligatorio ma è comunque fortemente raccomandabile (se non obbligatorio di fatto) ricondurre l’equazione data alla forma canonica. Diversamente, il metodo del completamento dei quadrati diverrebbe di più difficile applicazione.

Equazione in forma canonica di una circonferenza con centro nell’origine

Ripartiamo ancora dall’equazione in forma canonica di una generica circonferenza:

x^2+y^2+ax+by+c=0

Se la circonferenza ha centro nell’origine, abbiamo {x_C=0} ed {y_C=0}, poiché se il centro è l’origine entrambe le sue coordinate sono nulle.

Di conseguenza, per le ** abbiamo:

\overbrace{x_C}^{0}=-\dfrac{1}{2}a, \quad \overbrace{y_C}^0=-\dfrac{1}{2}b 

dalle quali segue per il nostro caso, rispettivamente:

\begin{align*} &-\dfrac{1}{2}a=0 \quad \Rightarrow \:a=0; \\ \\ & -\dfrac{1}{2}b=0 \quad \Rightarrow \: b=0\end{align*}

Di conseguenza per una circonferenza con centro nell’origine l’equazione in forma canonica si riduce a:

x^2+y^2+c=0 \qquad \text{circonferenza centrata nell'origine}

Tuttavia, anche in questo caso occorre verificare la condizione che la circonferenza sia reale non degenere. Poiché i coefficienti {a} e {b} per una circonferenza con centro nell’origine sono nulli, la condizione {\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0} si riduce a:

\small -c > 0 \qquad \text{condizione di circonferenza reale non degenere, solo se } C = (0,0)

Per cui, esclusivamente nel caso di una circonferenza centrata nell’origine, la circonferenza è reale non degenere se {-c > 0}, e quindi se il termine noto {c} è negativo.

Ora, dal confronto tra l’equazione con centro e raggio di una circonferenza centrata nell’origine, ovvero:

x^2+y^2=r^2

e l’equazione in forma canonica sempre di una circonferenza centrata nell’origine:

x^2+y^2+c=0

si ricava che:

r^2=-c

da cui:

r=\sqrt{-c}

Lo stesso risultato si ritrova a partire dalla formula, relativa ad una generica circonferenza:

r=\sqrt{x_C^2+y_C^2-c}

sostituendo in essa {x_C=0} ed {y_C=0} (coordinate del centro entrambe nulle per una circonferenza centrata nell’origine).

Equazione in forma canonica di una circonferenza passante per l’origine

Di nuovo, considerando ancora una volta l’equazione in forma canonica di una generica circonferenza:

x^2+y^2+ax+by+c=0

se questa è passante per l’origine, il punto {O=(0,0)} dovrà appartenere alla circonferenza. Così, sostituendo il valore {0} ad entrambe le incognite {x} ed {y}, dalla precedente otteniamo:

0^2+0^2+a\cdot0+b\cdot0+c=0 \quad \Rightarrow \quad c=0

Di conseguenza, nell’equazione canonica di una circonferenza passante per l’origine il termine noto {c} deve essere nullo:

x^2+y^2+ax+by=0 \qquad \text{circonferenza passante per l'origine}

Conclusioni

Per quanto riguarda l’equazione della circonferenza con centro e raggio ed in forma canonica è tutto. Riassumendo nella lezione abbiamo visto:

• come scrivere l’equazione di una circonferenza espressa con centro e raggio e nella forma canonica;
• come passare dall’equazione in forma canonica a quella con centro e raggio e viceversa;
• inoltre, come ricavare le coordinate del centro e il raggio a partire dall’equazione canonica di una circonferenza;
• l’utilizzo del metodo del completamento dei quadrati per ricavare le coordinate del centro e del raggio a partire dall’equazione in forma canonica di una circonferenza;
• infine, i casi particolari di circonferenze con centro nell’origine oppure passanti per l’origine.

Buon proseguimento con SìMatematica!