Intersezione tra retta e circonferenza

 - 

Circonferenza (scuole superiori)

L’operazione di intersezione tra una retta e una circonferenza consiste nel verificare se esistono tra la retta e la circonferenza stesse degli eventuali punti in comune, detti punti di intersezione. In particolare, se si ottengono due punti di intersezione diremo che la retta è secante alla circonferenza, se si ottiene un solo punto di intersezione diremo che la retta è tangente alla circonferenza, ed infine se non si ottiene alcun punto di intersezione concluderemo che la retta e la circonferenza non si intersecano tra loro.

L’intersezione tra retta e circonferenza è un caso particolare di un’operazione più generale, ovvero l’intersezione tra enti geometrici. L’intersezione tra retta e circonferenza permette quindi di ricercare gli eventuali punti di intersezione tra i due enti.

Come già abbiamo visto nelle precedenti lezioni, la geometria analitica fa uso dell’algebra per risolvere i problemi. Nel caso in esame, l’intersezione tra retta e circonferenza viene effettuata ricorrendo ai sistemi di equazioni, del tipo non lineari. Tuttavia, la risoluzione di tali sistemi non è complicata ed è basata unicamente sul principio di sostituzione e sulle tecniche risolutive relative alle equazioni di secondo grado.

Nello specifico, vedremo che determinare gli eventuali punti di intersezione tra una retta e una circonferenza equivale a risolvere un’equazione di secondo grado, detta equazione risolvente. E tale equazione si ottiene per sostituzione a partire da un sistema contenente l’equazione della retta e l’equazione della circonferenza in esame.

Ricordiamo che nel risolvere le equazioni di secondo grado si incontrano tre casi possibili: due soluzioni reali e distinte, due soluzioni reali e coincidenti e infine nessuna soluzione reale. Per l’equazione risolvente il problema dell’intersezione tra retta e circonferenza, a questi tre casi corrispondono rispettivamente le situazioni di retta secante alla circonferenza, retta tangente alla circonferenza ed infine di retta e circonferenza prive di punti di intersezione tra loro.

Come determinare i punti di intersezione tra retta e circonferenza

Consideriamo una circonferenza reale non degenere, che indicheremo con {\gamma}, avente equazione espressa ad esempio in forma canonica:

\gamma: x^2+y^2+ax+by+c=0, \qquad \text{con}  \quad \underbrace{\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0}_{\substack{\text{condizione per circonferenza} \\ \text{reale non degenere }}}

Ricordiamo che per circonferenza “reale non degenere” si intende una circonferenza avente per raggio un numero reale positivo non nullo.

Inoltre, consideriamo una retta {r_1} avente equazione, data ad esempio in forma implicita:

r_1 : a_1x+b_1y+c_1=0

Il nostro obiettivo è determinare, se esistono, le coordinate dei punti di intersezione tra la retta {r_1} e la circonferenza {\gamma}. Più formalmente, ci domandiamo se e quali punti del piano si ottengono effettuando l’operazione di intersezione tra la retta {r_1} e la circonferenza {\gamma}. Indichiamo formalmente tale operazione con:

r_1 \cap \gamma

Il simbolo di intersezione è lo stesso di quello utilizzato nella teoria degli insiemi. Infatti, la retta {r_1} e la circonferenza {\gamma} sono degli insiemi (o luoghi) di punti.

Ora, grazie all’algebra possiamo trovare gli eventuali punti di intersezione tra la retta e la circonferenza risolvendo il seguente sistema:

\begin{cases}\gamma: x^2+y^2+ax+by+c=0 \\ \\  r_1 : a_1x+b_1y+c_1=0\end{cases}

sistema nel quale figurano, rispettivamente, l’equazione della circonferenza e l’equazione della retta sulle quali effettuiamo l’operazione di intersezione.

Mettiamo le equazioni a sistema poiché ricerchiamo quei punti tali da soddisfare contemporaneamente sia la condizione di appartenenza alla circonferenza, sia la condizione di appartenenza alla retta. E come sappiamo dalle precedenti lezioni, affinché un punto appartenga ad un certo ente geometrico, le coordinate del punto dovranno soddisfare l’equazione che rappresenta l’ente geometrico stesso. Di conseguenza, ogni eventuale punto di intersezione tra la retta e la circonferenza dovrà necessariamente soddisfare entrambe le rispettive equazioni.

Osserviamo che il sistema non è lineare (ovvero non è di primo grado). Infatti, l’equazione della circonferenza è di secondo grado sia rispetto alla lettera {x}, sia rispetto alla lettera {y}. Tuttavia, in questo particolare caso la risoluzione del sistema è piuttosto agevole, e si basa sull’utilizzo del principio di sostituzione.

Il primo passo consiste nel riscrivere l’equazione della retta in forma esplicita ovvero, secondo la definizione, nell’esplicitare la variabile {y}. In alternativa, nel caso di una retta verticale sarà comunque possibile esplicitare la variabile {x}. Si otterrà così in ogni caso l’espressione di una variabile in funzione dell’altra.

Ad esempio, se esplicitiamo dall’equazione della retta la variabile {y}, otterremo per la variabile {y} un’espressione ad essa equivalente che è funzione della variabile {x}. Così, sostituendo tale espressione nell’equazione della circonferenza, ci ricondurremo ad un’equazione di secondo grado nella sola incognita {x}, che è possibile risolvere.

L’equazione di secondo grado in una variabile che così si ottiene è detta equazione risolvente per il sistema dato. Le eventuali soluzioni reali dell’equazione rappresentano le coordinate in {x} dei punti di intersezione tra la retta e la circonferenza date. Infine, sostituendo tali coordinate nell’equazione della retta sarà possibile ricavare le coordinate in {y} dei punti di intersezione.

Per l’intersezione tra retta e circonferenza abbiamo in particolare tre casi, ciascuno dipendente dal segno del determinante {\Delta} dell’equazione di secondo grado risolvente il sistema.

In particolare, se il determinante dell’equazione risolvente è maggiore di zero, l’equazione ammette due soluzioni reali e distinte. Di conseguenza, la circonferenza e la retta avranno due punti in comune. Quindi, l’operazione di intersezione tra i due enti geometrici darà come risultato due punti del piano. E in questa circostanza diremo che la retta è secante alla circonferenza.

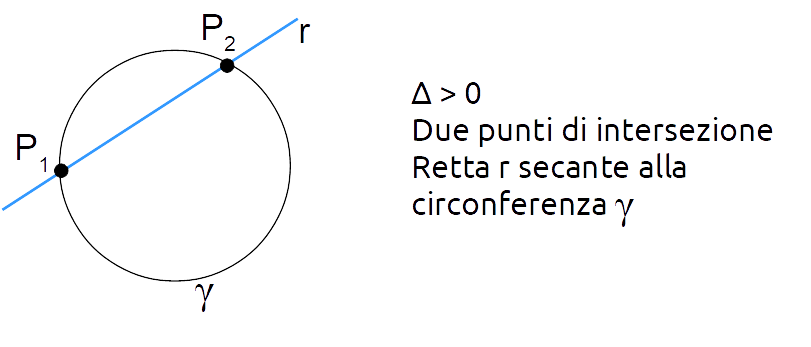
Se invece il determinante dell’equazione risolvente è uguale a zero, l’equazione ammette due soluzioni reali e coincidenti. Di conseguenza abbiamo un unico punto di intersezione tra la circonferenza e la retta. Diremo quindi che la retta è tangente alla circonferenza.

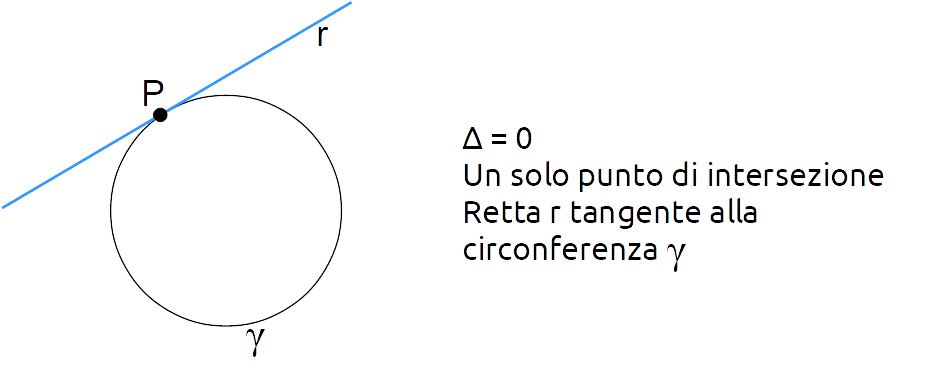
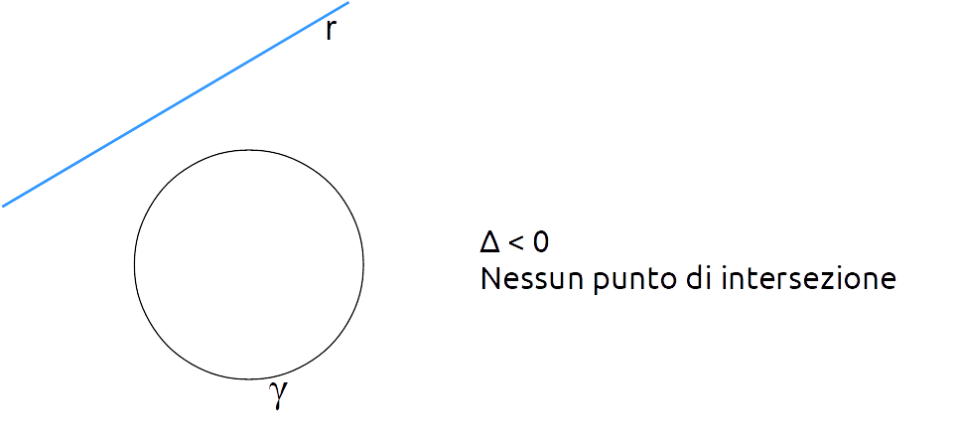
Infine, se il determinante dell’equazione risolvente è negativo, non esistono soluzioni reali per tale equazione. Perciò, la retta e la circonferenza non hanno punti di intersezione tra loro. Formalmente, diremo che l’operazione di intersezione tra i due enti geometrici considerati fornisce come risultato l’insieme vuoto.

Vediamo subito alcuni esempi su come determinare i punti di intersezione tra una retta e una circonferenza del piano cartesiano.

Esempio 1

Ricercare gli eventuali punti di intersezione tra la circonferenza {\gamma} di equazione {x^2+y^2+2x-3y-7=0} e la retta {r_1} di equazione {x+2y-5=0}.

Il primo passo consiste nel mettere a sistema le equazioni della circonferenza e della retta. Infatti, mettendo a sistema due equazioni richiediamo che queste siano soddisfatte contemporaneamente. Così, ricerchiamo i punti tali da soddisfare la condizione di appartenenza sia alla circonferenza, sia alla retta. E tali punti sono i punti di intersezione tra la retta e la circonferenza.

\begin{cases}\gamma: x^2+y^2+2x-3y-7=0 \\ \\ r_1:  x+2y-5=0\end{cases}

Riscriviamo l’equazione della retta in forma esplicita. In tal modo, isoliamo la variabile {y}:

\begin{cases}\gamma: x^2+y^2+2x-3y-7=0 \\ \\ r_1: y=\dfrac{-x+5}{2}\end{cases}

Nota: per comodità non conviene scrivere l’equazione della retta come {y=-\dfrac{1}{2}x+\dfrac{5}{2}}, anche se quest’ultima scrittura rappresenta più correttamente la forma esplicita.

Ora, siamo riusciti ad esprimere la variabile {y} in funzione della variabile {x}. Così, l’idea è quella di sostituire ad ogni lettera {y} nell’equazione della circonferenza l’espressione {\dfrac{-x+5}{2}}:

\begin{cases}\gamma: x^2+\left( \dfrac{-x+5}{2}\right)^2+2x-3 \cdot\left( \dfrac{-x+5}{2}\right)-7=0 \\ \\ r_1: y=\dfrac{-x+5}{2}\end{cases}

Ora l’equazione della circonferenza è nella sola incognita {x}. Di conseguenza, sarà possibile risolvere l’equazione rispetto ad {x}. Concentriamoci sulla sola equazione della circonferenza così riespressa e sviluppiamo i calcoli:

\begin{align*} & x^2+\left( \dfrac{-x+5}{2}\right)^2+2x-3 \cdot\left( \dfrac{-x+5}{2}\right)-7=0;\\ \\ &x^2+\dfrac{x^2-10x+25}{4}+2x+\dfrac{3x-15}{2}-7=0;\\ \\ & \dfrac{4x^2+x^2-10x+25+8x+6x-30-28}{\cancel{4}} =0;\\ \\ & 5x^2+4x-33=0\end{align*}

Abbiamo così ottenuto un’equazione di secondo grado in forma normale nella sola incognita {x}, che è l’equazione risolvente il sistema.

Ricordiamo che un’equazione di secondo grado in forma normale si scrive come:

ax^2+by+c=0

Nel nostro caso, per i coefficienti che compaiono nell’equazione abbiamo i seguenti valori:

a=5, \quad b = 4, \quad c=-33

Per il determinante di tale equazione abbiamo:

\Delta = b^2-4ac=4^2-4 \cdot 5 \cdot (-33) =16+4 \cdot 5 \cdot 33 > 0

Il determinante è maggiore di zero e di conseguenza l’equazione ammetterà due soluzioni reali e distinte. E poiché si tratta del determinante dell’equazione risolvente il sistema, da qui già possiamo dire che la circonferenza e la retta hanno due punti di intersezione.

Possiamo a questo punto risolvere l’equazione utilizzando la ormai nota formula risolutiva:

\begin{align*} & x_{1,2}=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}=\dfrac{-4\pm\sqrt{16-4 \cdot 5 \cdot (-33)}}{2 \cdot 5}=\dfrac{-4 \pm \sqrt{16+660}}{10}=\\ \\ & =\dfrac{-4 \pm \sqrt{676}}{10} =\dfrac{-4 \pm 26}{10}= \begin{cases} \dfrac{11}{5} \\ \\ -3\end{cases}\end{align*}

Abbiamo così ottenuto i valori {x_1 = \dfrac{11}{5}} ed {x_2 = -3}, che rappresentano le ascisse (coordinate lungo l’asse {x}) dei punti di intersezione tra la retta e la circonferenza.

Per ottenere i valori delle ordinate, basta ritornare al sistema con l’equazione della retta in forma esplicita, che per comodità riscriviamo:

\begin{cases}\gamma: x^2+y^2+2x-3y-7=0 \\ \\ r_1: y=\dfrac{-x+5}{2}\end{cases}

e considerare l’equazione della retta.

In pratica, basta sostituire ciascun valore della {x} nell’equazione della retta, ottenendo i corrispondenti valori della {y}, ovvero le ordinate (o coordinate lungo l’asse {y}) dei punti di intersezione tra la circonferenza e la retta. Abbiamo in particolare:

\begin{align*}  &y=\dfrac{-x+5}{2} \quad \text{con} \quad x=\dfrac{11}{5} \quad \Rightarrow \quad y=\dfrac{-\dfrac{11}{5}+5}{2}=\dfrac{7}{5}; \\ \\ & y=\dfrac{-x+5}{2} \quad \text{con} \quad x=-3 \quad \Rightarrow \quad y=\dfrac{-(-3)+5}{2}=4\end{align*}

Così in conclusione, indicando con {P_1} e {P_2} i punti di intersezione tra la circonferenza e la retta abbiamo:

P_1=\left( \dfrac{11}{5}, \dfrac{7}{5}\right), \qquad P_2=\left( -3, 4\right)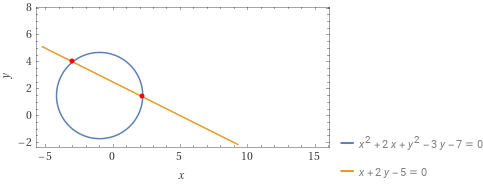

Esempio 2

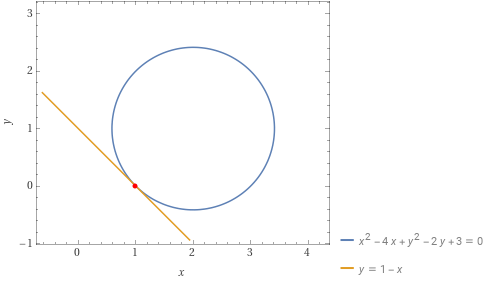
Ricercare gli eventuali punti di intersezione tra la circonferenza {\gamma} di equazione {x^2+y^2-4x-2y+3=0} e la retta {r_1} di equazione {y=-x+1}.

Come nell’esempio precedente, si tratterà di risolvere il sistema:

\begin{cases} \gamma: x^2+y^2-4x-2y+3=0 \\ \\ r_1: y=-x+1 \end{cases}

L’equazione della retta è già in forma esplicita, per cui possiamo direttamente sostituire l’espressione {-x+1} ad ogni lettera {y} nell’equazione della circonferenza:

\begin{cases} x^2+(-x+1)^2-4x-2(-x+1)+3=0 \\ \\ y=-x+1\end{cases}

Concentriamoci sulla sola prima equazione del sistema:

\begin{align*} &x^2+(-x+1)^2-4x-2(-x+1)+3=0; \\ \\&x^2+x^2-2x+1-4x+2x-2+3=0;\\ \\ & 2x^2-4x+2=0; \\ \\ & x^2-2x+1=0 & \end{align*}

Per il discriminante o determinante dell’equazione risolvente appena ottenuta abbiamo:

\Delta =b^2-4ac=(-2)^2-4 \cdot 1 \cdot 1 =4-4=0

Il determinante è nullo per cui ci aspettiamo per l’equazione risolvente due soluzioni reali e coincidenti. Come sappiamo, a tale casistica corrisponde l’esistenza di un solo punto di intersezione tra la circonferenza e la retta. Così, già possiamo affermare che la retta {r_1} è tangente alla circonferenza {\gamma}.

Risolviamo l’equazione:

x_{1,2}=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}=\dfrac{2\pm \sqrt{0}}{2\cdot1}=\dfrac{2}{2}=1

Abbiamo quindi ottenuto per l’incognita {x} due valori tra loro uguali. Di conseguenza, il solo punto di intersezione tra la circonferenza e la retta in esame ha ascissa {x=1}. Per l’ordinata, sostituendo tale valore nell’equazione della retta:

y=-x+1=-1+1=0

Così il solo punto di intersezione tra la circonferenza {\gamma} e la retta {r_1} è:

P=(1,0)

e possiamo affermare che la retta {r_1} è tangente alla circonferenza proprio in questo punto.

Esempio 3

Ricercare gli eventuali punti di intersezione tra la circonferenza {\gamma} di equazione {x^2+y^2+3x+4y-5=0} e la retta {r_1} di equazione {2x+3y-8=0}.

Impostiamo il sistema:

\begin{cases} \gamma: x^2+y^2+3x+4y-5=0 \\ \\ r_1: 2x+3y-8=0\end{cases}

Riscriviamo l’equazione della retta in forma esplicita:

\begin{cases} \gamma: x^2+y^2+3x+4y-5=0 \\ \\ r_1: y=\dfrac{-2x+8}{3}\end{cases}

Ora sostituiamo l’espressione ottenuta per {y} nella prima equazione a sistema:

\begin{cases} \gamma: x^2+\left( \dfrac{-2x+8}{3}\right)^2+3x+4\left( \dfrac{-2x+8}{3}\right)-5=0 \\ \\ r_1: y=\dfrac{-2x+8}{3}\end{cases}

Concentriamoci a questo punto sulla sola prima equazione:

\begin{align*} & x^2+\left( \dfrac{-2x+8}{3}\right)^2+3x+4\left( \dfrac{-2x+8}{3}\right)-5=0; \\ \\ & x^2+\dfrac{4x^2-32x+64}{9}+3x+\dfrac{-8x+32}{3}-5=0;\\ \\ & \dfrac{9x^2+4x^2-32x+64+27x-24x+96-45}{\cancel{9}}=0; \\ \\ & 13x^2-29x+115=0\end{align*}

Vediamo ora cosa succede per il {\Delta} dell’equazione risolvente appena ottenuta:

\Delta=b^2-4ac=(-29)^2-4 \cdot 13 \cdot 115 =841 -5980 < 0

Poiché il {\Delta} dell’equazione risolvente è negativo, non esistono soluzioni reali per l’equazione stessa e di conseguenza concludiamo che non esistono punti di intersezione tra la circonferenza e la retta date.

Intersezione tra una circonferenza e una retta orizzontale o verticale

I casi sin qui visti sono quelli più generali. Nel caso di una retta orizzontale o verticale, il problema dell’intersezione tra una circonferenza e una tale retta si semplifica notevolmente.

Esempio 4

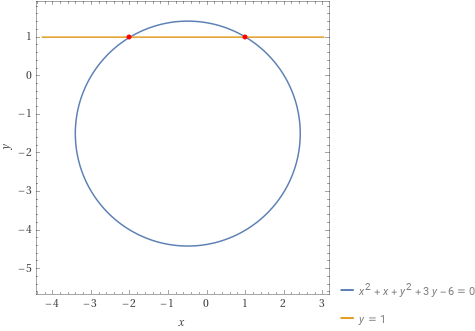
Determinare gli eventuali punti di intersezione tra la circonferenza {\gamma} di equazione {x^2+y^2+x+3y-6=0} e la retta {r_1} di equazione {y=1}.

Osserviamo che la retta {y=1} è orizzontale. Infatti, l’ordinata di tutti i punti appartenenti alla retta è sempre la stessa (vedi: equazione di una retta nel piano). Siamo così di fronte al problema relativo a come determinare gli eventuali punti di intersezione tra una circonferenza ed una retta orizzontale.

Il sistema che dobbiamo risolvere è il seguente:

\begin{cases} \gamma: x^2+y^2+x+3y-6=0 \\ \\ r_1: y=1\end{cases}

In questo caso si tratta semplicemente di sostituire alle lettere {y} dell’equazione della circonferenza il valore {1}. Otteniamo l’equazione di secondo grado:

x^2+1+x+3-6=0

ovvero:

x^2+x-2=0

che risolta fornisce:

x_{1,2}=\dfrac{-1\pm \sqrt{1^2-4 \cdot 1 \cdot (-2)}}{2}=\dfrac{-1\pm 3}{2}=\begin{cases} 1 \\ \\ -2\end{cases}

Di conseguenza abbiamo due punti di intersezione tra la retta e la circonferenza, aventi ascisse:

x_1=1, \qquad x_2= -2

In generale, come visto negli esempi precedenti, sostituendo questi valori nell’equazione della retta otteniamo le corrispondenti ordinate. Nel caso in esame, tuttavia, poiché non figura alcuna lettera {x} nell’equazione della retta, semplicemente abbiamo:

y_1=1, \qquad y_2=1

In altre parole, poiché la retta {r_1} è orizzontale, entrambi i punti di intersezione dovranno necessariamente avere la stessa ordinata, uguale al valore che figura nell’equazione della retta {y=1}.

Così in conclusione l’intersezione tra la circonferenza {\gamma} e la retta {r_1} ha come risultato i punti:

P_1=(1,1), \qquad P_2=(-2,1)

Esempio 5

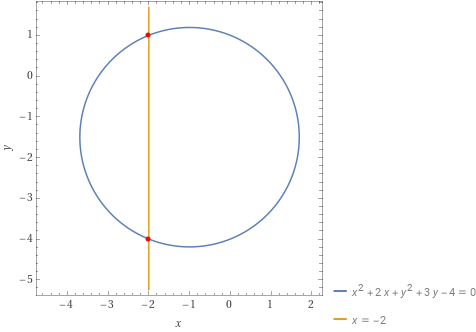
Determinare gli eventuali punti di intersezione tra la circonferenza {\gamma} di equazione {x^2+y^2+2x+3y-4=0} e la retta {r_1} di equazione {x=-2}.

In questo caso la retta {r_1} è verticale. Infatti, tutti i suoi punti condividono lo stesso valore dell’ascissa, ovvero {-2}. Di conseguenza, ci ritroviamo davanti al problema relativo alla determinazione del punto di intersezione tra una circonferenza ed una retta verticale.

Il sistema da impostare è il seguente:

\begin{cases} \gamma: x^2+y^2+2x+3y-4=0 \\ \\ r_1: x=-2\end{cases}

Osserviamo che avendo a che fare con una retta verticale, la sua equazione non può essere esplicitata rispetto alla variabile {y}. Ciò tuttavia non è affatto un problema. Anche se qui diversamente dai casi precedenti non possiamo effettuare alcuna sostituzione rispetto alla lettera {y}, basterà semplicemente sostituire nell’equazione della circonferenza a ciascuna lettera {x} il valore {-2}.

Così abbiamo per la prima equazione a sistema:

\begin{align*} & x^2+y^2+2x+3y-4=0  \quad \text{con} \quad x=-2\\ \\ & \Rightarrow (-2)^2+y^2+2\cdot(-2)+3y-4=0 \\ \\ & \Rightarrow y^2+3y-4=0\end{align*}

Ricerchiamo le eventuali soluzioni dell’equazione risolvente. Questa si presenta ora nella variabile {y}, ma ciò non comporta alcun cambiamento nel metodo risolutivo.

y_{1,2}=\dfrac{-3 \pm \sqrt{3^2-4 \cdot 1 \cdot (-4)}}{2 \cdot 1}=\dfrac{-3\pm 5}{2}=\begin{cases} 1 \\ \\ -4\end{cases}

Così le ordinate (coordinate lungo l’asse {y}) dei punti di intersezione tra la circonferenza e la retta date sono rispettivamente {y_1=1} e {y_2=-4}. Poiché l’equazione della retta è {x=-2} (con ascissa costante), le ascisse di entrambi i punti di intersezione saranno necessariamente uguali a {-2}. Il discorso è infatti del tutto simile a quello fatto nell’esempio precedente.

In conclusione i punti di intersezione tra la circonferenza {\gamma} e la retta {r_1} sono:

P_1=(-2,1), \qquad P_2=(-2,-4)

Ricerca dei punti di intersezione tra una circonferenza e uno fra gli assi x ed y

Precisiamo infine che dato che le equazioni degli assi {x} ed {y} sono rispettivamente:

y=0, \qquad x=0

le considerazioni degli ultimi due esempi si applicano rispettivamente anche ai casi della ricerca dei punti di intersezione tra una circonferenza e l’asse {x} e tra una circonferenza e l’asse {y}.

Conclusioni

Per quanto riguarda il problema dell’intersezione tra una retta e una circonferenza è tutto. Come abbiamo visto, in generale si tratta di risolvere un sistema non lineare. In realtà, tuttavia, i sistemi che qui si presentano non richiedono l’utilizzo di particolari tecniche. Si tratta infatti soltanto di effettuare un’opportuna sostituzione, ricadendo nel caso di una semplice equazione di secondo grado.

Infine, ricordiamo sempre che, nel problema dell’intersezione tra una retta ed una circonferenza, se l’equazione risolvente ha determinante uguale a zero, la retta risulterà necessariamente tangente alla circonferenza. In particolare, nella prossima lezione mostreremo che, sfruttando la condizione di determinante nullo dell’equazione risolvente, sarà possibile determinare l’equazione della retta tangente ad una circonferenza in un dato punto.

Volendo comunque fornire una breve anticipazione al problema, supponiamo di voler determinare l’equazione della retta tangente alla circonferenza:

\gamma: x^2+y^2+2x+2y-3=0

nel punto appartenente alla circonferenza stessa:

P=(1,0)

Diversamente da tutti gli esempi precedenti, non conosciamo l’equazione della retta. Tuttavia, questa dovrà necessariamente passare per il punto {P} di tangenza alla circonferenza. Questo punto infatti è comune ai due enti geometrici.

Di conseguenza, ricordando l’equazione della retta passante per un punto ed avente coefficiente angolare noto:

y-y_0=m(x-x_0)

nel nostro caso, indicando con {x_P} ed {y_P} le coordinate del punto {P} di tangenza, possiamo scrivere per l’equazione della retta {r_1}:

r_1: y-y_P=m(x-x_P)

ovvero, tenendo conto dei valori delle coordinate del punto {P}:

r_1: y=m(x-1)

Osserviamo che il coefficiente angolare {m} è incognito, poiché effettivamente non conosciamo ancora l’equazione della retta tangente alla circonferenza nel punto {P}.

Così, data l’equazione di {r_1} nella forma appena scritta, la coppia data dalle coordinate del punto {P} dovrà necessariamente soddisfare il sistema:

\begin{cases} \gamma: x^2+y^2+2x+2y-3=0 \\ \\  r_1: y=m(x-1)\end{cases}

Ma l’equazione di {r_1} ci fornisce un’espressione per la variabile {y} in funzione di {m} ed {x}. Così, sostituendo l’espressione {m(x-1)} al posto di ogni lettera {y} nell’equazione della circonferenza otteniamo:

\begin{cases} \gamma: x^2+\left[ m(x-1)\right]^2+2x+2[m(x-1)]-3=0 \\ \\  r_1: y=m(x-1)\end{cases}

Concentriamoci sulla prima equazione e sviluppiamone i calcoli:

\begin{align*} &x^2+m^2(x-1)^2+2x+2mx-2m-3=0; \\ \\ & x^2+m^2(x^2-2x+1)+2x+2mx-2m-3=0;\\ \\ & x^2+m^2x^2-2m^2x+m^2+2x+2mx-2m-3=0;\\ \\ & \underbrace{(1+m^2)}_{a}x^2+\underbrace{(-2m^2+2m+2)}_{b}x+\underbrace{m^2-2m-3}_{c}=0\end{align*}

Apparentemente ci ritroviamo in difficoltà, poiché l’equazione risolvente è nelle due incognite {m} ed {x}. Tuttavia, ricordiamo che dobbiamo scrivere l’equazione della retta tangente alla circonferenza in {P}. E ciò che ci serve è il solo coefficiente angolare {m}.

Ricordando ancora che per la condizione di tangenza deve essere:

\Delta =0

dall’equazione risolvente scritta, imponendo la condizione di tangenza ed osservando che i coefficienti dei suoi termini sono tutti funzioni di {m}, otteniamo l’equazione nella sola incognita {m}:

\begin{align*} &\Delta = b^2-4ac=0\\ \\ & \Rightarrow\underbrace{(-2m^2+2m+2)^2}_{\substack{\text{quadrato di} \\ \text{un trinomio}}}-4 (1+m^2)  \cdot (m^2-2m-3)=0;\\ \\ &4m^4+4m^2+4-8m^3-8m^2+8m-4(m^2-2m-3+m^4-2m^3-3m^2)=0;\\ \\ & \cancel{4m^4}+\cancel{4m^2}+4-\cancel{8m^3}-8m^2+8m-\cancel{4m^2}+8m+12-\cancel{4m^4}+\cancel{8m^3}+12m^2=0; \\ \\ &4m^2+16m+16=0;\\ \\ & m^2+4m+4=0 \end{align*}

Risolvendo l’equazione rispetto ad {m} otteniamo:

m_{1,2}=\dfrac{-4 \pm \sqrt{16-4 \cdot 1\cdot 4}}{2}=-2

Otteniamo così un solo valore per il coefficiente angolare. Ciò non deve stupire, poiché effettivamente la retta tangente ad una circonferenza in un suo punto è unica. Così, sostituendo il valore appena ottenuto per il coefficiente angolare nell’equazione della retta {r_1} otteniamo in conclusione:

r_1: y=-2(x-1)

ovvero:

r_1: y=-2x+2

e questa è l’equazione della retta tangente alla circonferenza {\gamma} nel punto {P} dato.

Come evidente, il metodo appena descritto presenta l’inconveniente di richiedere dei calcoli piuttosto lunghi. Ma nella prossima lezione, dopo aver spiegato più nel dettaglio questo stesso metodo, mostreremo dei procedimenti semplificati per il caso della ricerca dell’equazione della retta tangente ad una circonferenza in un suo punto.

Un saluto a tutti voi e, come sempre, buono studio con SìMatematica!