Tangente ad una circonferenza in un suo punto

 - 

Circonferenza (scuole superiori)

Il metodo più generale per determinare l’equazione della retta tangente ad una circonferenza in un punto della circonferenza stessa consiste nell’imporre la condizione di determinante dell’equazione risolvente uguale a zero. Il procedimento si basa su quanto già visto a proposito della ricerca degli eventuali punti di intersezione tra una retta e una circonferenza.

Tuttavia, tale metodo non è il più efficiente. In particolare, mostreremo come determinare più rapidamente l’equazione della retta tangente ad una circonferenza in un suo punto sfruttando un’opportuna relazione di perpendicolarità oppure facendo uso di formule specifiche, dette formule di sdoppiamento.

In verità ci siamo già occupati di questi metodi nella prima lezione sulla circonferenza, ma nel corso di questa lezione riprenderemo ancora più nel dettaglio ciascun procedimento, fornendo i relativi esercizi di esempio, ripartendo da zero. Di conseguenza, anche senza aver letto la lezione indicata nel link sarà comunque possibile studiare i metodi per determinare l’equazione della retta tangente ad una circonferenza in un suo punto

Un’importante precisazione. In questa lezione ci occupiamo del problema di determinare l’equazione della retta tangente ad una circonferenza in un punto appartenente alla circonferenza stessa. Del problema invece relativo a come determinare le rette tangenti ad una circonferenza passanti per un punto esterno alla circonferenza stessa ci occuperemo nella lezione successiva. E per quest’ultimo problema, oltre al metodo più generale basato sull’equazione risolvente, mostreremo anche come cavarcela utilizzando la formula della distanza tra una retta ad un punto.

Tecniche per la determinazione dell’equazione della retta tangente ad una circonferenza in un suo punto

Cominciamo subito ad esaminare ciascuna delle principali tecniche grazie alle quali è possibile determinare l’equazione della retta tangente ad una circonferenza in un punto appartenente alla circonferenza stessa.

Utilizzo di un’opportuna relazione di perpendicolarità

Consideriamo una circonferenza {\gamma} reale non degenere con equazione scritta ad esempio in forma canonica:

\gamma : x^2+y^2+ax+by+c=0

Consideriamo inoltre un punto {P} appartenente alla circonferenza, avente coordinate note:

P=(x_P, y_P)

Possiamo rappresentare la retta {t} tangente alla circonferenza nel punto {P} come segue:

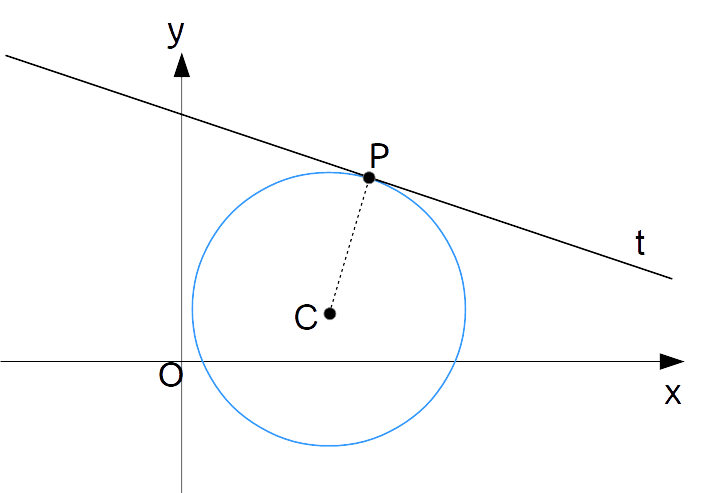
Nella figura, con {C} è indicato il centro della circonferenza:

C=(x_C, y_C)

Se l’equazione della circonferenza è data in forma canonica, possiamo ricavare le coordinate del centro della circonferenza con le formule già note:

x_C=-\dfrac{1}{2}a, \quad y_C=-\dfrac{1}{2}b

Ricordando poi la formula del coefficiente angolare, possiamo esprimere il coefficiente angolare della retta passante per {C} e {P} come:

m_{CP}=\dfrac{y_P-y_C}{x_P-x_C}

ovviamente sotto la condizione {x_P \neq x_C}.

Ora, dalla geometria elementare sappiamo che la retta {t} è perpendicolare alla retta che passa per i punti {C} e {P}. Ciò si vede immediatamente dalla figura, poiché il segmento {\overline{CP}} è perpendicolare alla retta tangente {t}.

Di conseguenza, il coefficiente angolare {m} della retta {t} si può ricavare a partire dal coefficiente angolare {m_{CP}} come:

m=-\dfrac{1}{m_{CP}}

Ciò si basa sulla condizione di perpendicolarità fra rette. Prestiamo attenzione che la relazione è valida soltanto nel caso in cui la retta {r_{CP}} (ovvero la retta passante per i punti {C} e {P}) non sia parallela all’asse {x} o all’asse {y}. In altre parole, la precedente relazione non è valida se la retta per {C} e {P} è orizzontale oppure verticale.

Ora ci basta soltanto osservare che il punto {P} appartiene necessariamente alla retta tangente {t}. Di conseguenza, tenendo conto della formula della retta di pendenza nota passante per un dato punto, possiamo scrivere l’equazione della retta {t}:

t:y-y_P=m(x-x_P)

Vediamo subito degli esempi su come determinare l’equazione della retta tangente alla circonferenza in un suo punto, utilizzando la condizione di perpendicolarità fra rette.

Esempio 1

Determinare l’equazione della retta {t} tangente alla circonferenza reale non degenere {\gamma : x^2+y^2+2x-4y-8=0} nel suo punto {P=(1,5)}.

L’equazione della circonferenza è data in forma canonica, ovvero:

x^2+y^2+ax+by+c=0

con i seguenti valori dei coefficienti {a} e {b}:

a=2, \: b=-4

Di conseguenza, le coordinate del centro della circonferenza sono:

x_C=-\dfrac{1}{2}a=-\dfrac{1}{2}\cdot2=-1; \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot (-4)=2

Essendo anche note le coordinate del punto {P}, ed essendo soddisfatta la condizione {x_P \neq x_C}, possiamo calcolare il coefficiente angolare della retta passante per {C} e {P}:

m_{CP}=\dfrac{y_P-y_C}{x_P-x_C}=\dfrac{5-2}{1-(-1)}=\dfrac{3}{2}

A questo punto, poiché la retta passante per {C} e {P} è perpendicolare alla retta tangente {t}, il coefficiente angolare {m} di quest’ultima è dato da:

m=-\dfrac{1}{m_{CP}}=-\dfrac{1}{\frac{3}{2}}=-\dfrac{2}{3}

Quindi, ricordando la formula della retta passante per un punto con coefficiente angolare noto, tenendo conto che la retta tangente passa necessariamente per il punto {P}, abbiamo:

t: y-\underbrace{5}_{y_P}=\underbrace{-\dfrac{2}{3}}_{m} \cdot (x-\underbrace{1}_{x_P})

Esprimendo infine la retta tangente ad esempio in forma esplicita abbiamo con qualche rapido calcolo:

t: y=-\dfrac{2}{3}x+\dfrac{17}{3}

E questa è l’equazione in forma esplicita della retta tangente alla circonferenza data nel punto {P}.

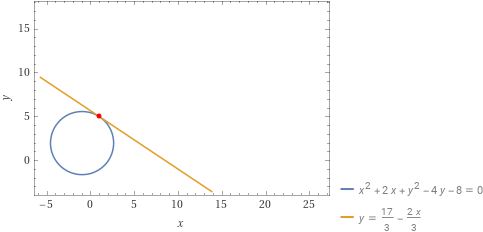
Esempio 2

Determinare l’equazione della retta tangente alla circonferenza {\gamma} reale non degenere di equazione {x^2+y^2-4x-4y-8=0} nel suo punto {P=(2,6)}.

Cominciamo determinando le coordinate del centro della circonferenza:

x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot (-4)=2; \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot (-4)=2

Di conseguenza la circonferenza ha centro {C=(2,2)}.

E’ fondamentale osservare che il centro {C} e il punto {P} condividono la stessa ascissa, infatti abbiamo {x_C=x_P=2}. Ciò significa che non è possibile calcolare il coefficiente angolare della retta passante per i punti {C} e {P}, infatti nella seguente uguaglianza:

m_{CP}=\dfrac{y_P-y_C}{x_P-x_C}

il denominatore al secondo membro in questo caso si annulla. E ciò non è accettabile (vedi: campo di esistenza di una frazione algebrica).

In particolare, ricordiamo che se i punti di una retta condividono la stessa ascissa, la retta stessa è verticale, ovvero della forma:

x=k, \qquad k \in \R

Così nel nostro caso la retta passante per {C} e {P} ha equazione:

r_{CP}: x=2

ed è verticale. E per le rette verticali, il coefficiente angolare non è definito. Non è quindi possibile utilizzare l’uguaglianza:

m=-\dfrac{1}{m_{CP}}

in quanto non esiste alcun valore da attribuire ad {m_{CP}}.

Tuttavia, per scrivere l’equazione della retta ad essa perpendicolare e passante per il punto di tangenza {P}, basta osservare che per la geometria elementare tale retta sarà necessariamente orizzontale, con equazione del tipo:

y=k, \qquad k \in \R

In altre parole, la perpendicolare ad una retta verticale è necessariamente orizzontale.

Ma quanto vale {k}? Poiché la retta è passante per {P}, e l’ordinata di {P} è {6}, avremo necessariamente {k=6}. Di conseguenza, l’equazione della retta perpendicolare ad {r_{CP}} e passante per {P} è:

y=6

e per quanto sin qui visto questa non è che la retta tangente alla circonferenza nel punto {P}.

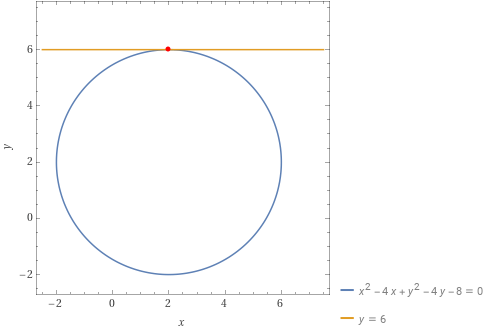
Esempio 3

Determinare l’equazione della retta tangente alla circonferenza reale non degenere {\gamma: x^2+y^2-4x-4y-17=0} nel punto {P=(-3,2)}.

Per le coordinate del centro della circonferenza abbiamo:

x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot (-4)=2; \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot (-4)=2

di conseguenza:

C=(2,2)

Osserviamo che il centro {C} e il punto {P} hanno in comune la stessa ordinata. Quindi si ha:

m_{CP}=\dfrac{y_P-y_C}{x_P-x_C}=0

poiché infatti {y_P=y_C}. E come sappiamo, se il coefficiente angolare di una retta è nullo, questa è orizzontale.

Ora, non possiamo ricavare il coefficiente angolare {m} utilizzando la relazione:

m=-\dfrac{1}{m_{CP}}

infatti questa non è valida nel caso in cui la retta {r_{CP}} sia verticale oppure, come nel nostro caso, orizzontale. E non a caso, provando ad utilizzare comunque tale uguaglianza il denominatore al secondo membro si annullerebbe.

Tuttavia, sappiamo che una retta orizzontale passante per il punto {P=(-3,2)} ha necessariamente equazione:

y=2

Ora, per la geometria elementare, una retta perpendicolare ad una retta orizzontale dovrà necessariamente essere verticale. Così una retta perpendicolare a {y=2} dovrà necessariamente avere un’equazione del tipo:

x=k, \qquad k \in \R

e poiché questa deve passare per {P=(-3,2)}, {k} deve necessariamente valere {-3}, ed abbiamo in conclusione l’equazione della retta tangente alla circonferenza data e passante per {P}:

t:x=-3

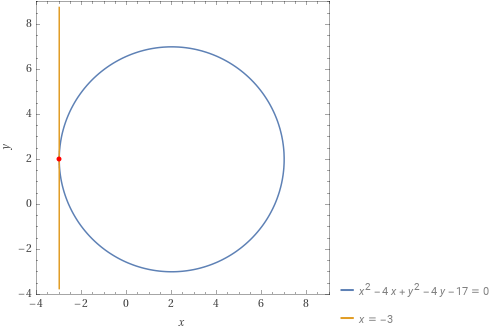
Formule di sdoppiamento della circonferenza

Un altro metodo per determinare l’equazione della retta tangente ad una circonferenza in un suo punto è dato dalle formule di sdoppiamento della circonferenza. Tali formule consentono di determinare l’equazione della retta tangente cercata a partire dall’equazione in forma canonica della circonferenza in esame, operando delle opportune sostituzioni.

In particolare, data l’equazione di una circonferenza reale non degenere in forma canonica:

x^2+y^2+ax+by+c=0

per ricercare la retta ad essa tangente nel punto:

P=(x_P, y_P)

si tratterà di operare nell’equazione della circonferenza data le sostituzioni:

x^2 \rightarrow x_P \cdot x, \qquad y^2 \rightarrow y_P \cdot y, \qquad x \rightarrow \dfrac{x+x_P}{2}, \qquad y \rightarrow \dfrac{y+y_P}{2}

In altre parole, bisogna sostituire nell’equazione in forma canonica della circonferenza ad {x^2} la quantità {x_P \cdot x}, ad {y^2} la quantità {y_P \cdot y} e così via.

Importante. Prima di utilizzare le formule di sdoppiamento occorre sempre assicurarsi che l’equazione della circonferenza sia in forma canonica, ovvero sia data esclusivamente da una somma di monomi tra loro non simili.

Vediamo subito l’utilizzo delle formule di sdoppiamento per la circonferenza riprendendo i tre esempi precedenti.

Esempio 1 bis

Determinare l’equazione della retta {t} tangente alla circonferenza reale non degenere {\gamma : x^2+y^2+2x-4y-8=0} nel suo punto {P=(1,5)}. Utilizzare le formule di sdoppiamento.

Osserviamo che per applicare le formule di sdoppiamento non abbiamo bisogno delle coordinate del centro della circonferenza. Ci basta conoscere soltanto l’equazione in forma canonica della circonferenza e il punto di tangenza {P}. Questo è un evidente vantaggio rispetto al metodo che si basa sulla relazione di perpendicolarità tra rette. Tuttavia, dobbiamo ricordare le sostituzioni da eseguire sull’equazione della circonferenza.

Nel nostro caso il punto di tangenza è {P=(1,5)}. Abbiamo quindi:

x_P=1; \qquad y_P=5

Ora, le sostituzioni da eseguire, che in generale sono:

x^2 \rightarrow x_P \cdot x, \qquad y^2 \rightarrow y_P \cdot y, \qquad x \rightarrow \dfrac{x+x_P}{2}, \qquad y \rightarrow \dfrac{y+y_P}{2}

nel nostro particolare caso, tenendo conto dei valori di {x_P} e {y_P}, divengono:

x^2 \rightarrow 1 \cdot x, \qquad y^2 \rightarrow 5 \cdot y, \qquad x \rightarrow \dfrac{x+1}{2}, \qquad y\rightarrow \dfrac{y+5}{2}

ovvero:

x^2 \rightarrow x, \qquad y^2\rightarrow 5y, \qquad x \rightarrow \dfrac{x+1}{2}, \qquad y \rightarrow \dfrac{y+5}{2}

Così, a partire dall’equazione della circonferenza in forma canonica:

 x^2+y^2+2x-4y-8=0

effettuando tali sostituzioni abbiamo:

\underbrace{x}_{x^2}+\underbrace{5y}_{y^2}+2 \cdot \underbrace{\left( \dfrac{x+1}{2}\right)}_{x}-4 \cdot \underbrace{\left( \dfrac{y+5}{2}\right)}_{y}-8=0

Come possiamo vedere, grazie a tali sostituzioni l’equazione della circonferenza diviene un’equazione di primo grado rispetto ad entrambe le variabili. Svolgendo i calcoli al primo membro:

x+5y+x+1-2y-10-8=0

otteniamo in conclusione:

t:2x+3y-17=0

Questa è l’equazione della retta tangente alla circonferenza data nel punto {P}.

Il risultato è lo stesso di quello ottenuto con il procedimento dell’esempio 1. Infatti, basta riscrivere l’equazione della retta {t} in forma esplicita, ovvero nella forma {y=mx+q}:

\begin{align*}&3y=-2x+17; \\ \\ & y=\dfrac{-2x+17}{3}; \\ \\ & t: y=-\dfrac{2}{3}x+\dfrac{17}{3} &\end{align*}

Ritroviamo così anche con le formule di sdoppiamento lo stesso risultato dell’esempio precedente.

Esempio 2 bis

Determinare l’equazione della retta tangente alla circonferenza {\gamma} reale non degenere di equazione {x^2+y^2-4x-4y-8=0} nel suo punto {P=(2,6)}. Utilizzare le formule di sdoppiamento.

Nel nostro caso, essendo {P=(2,6)} abbiamo {x_P=2} e {y_P=6}. Per cui le formule di sdoppiamento divengono:

x^2 \rightarrow 2x, \qquad y^2\rightarrow 6y, \qquad x\rightarrow \dfrac{x+2}{2}, \qquad y\rightarrow \dfrac{y+6}{2}

Così operando tali sostituzioni nell’equazione in forma canonica della circonferenza in esame, abbiamo:

2x+6y-4 \cdot \left( \dfrac{x+2}{2}\right)-4\cdot\left(\dfrac{y+6}{2} \right)-8=0

Effettuando i calcoli al primo membro:

\cancel{2x}+6y-\cancel{2x}-4-2y-12-8=0

ovvero:

t:4y=24

e infine, semplificando:

t:y=6

Questa è la retta tangente alla circonferenza nel punto {P}. Ed il risultato è lo stesso di quello ottenuto nell’esempio 2.

Esempio 3 bis

Determinare l’equazione della retta tangente alla circonferenza reale non degenere {\gamma: x^2+y^2-4x-4y-17=0} nel punto {P=(-3,2)}. Utilizzare le formule di sdoppiamento.

Abbiamo:

x^2 \rightarrow -3x, \qquad y^2 \rightarrow 2y, \qquad x\rightarrow \dfrac{x-3}{2}, \qquad y\rightarrow \dfrac{y+2}{2}

e quindi operando tali sostituzioni nell’equazione della circonferenza:

\begin{align*} & -3x+2y-4 \cdot \left( \dfrac{x-3}{2}\right)-4 \cdot \left( \dfrac{y+2}{2}\right)-17=0;  \\ \\ & -3x+\cancel{2y}-2x+6-\cancel{2y}-4-17=0;\\ \\ & -5x-15=0\end{align*}

da cui otteniamo in conclusione l’equazione della retta tangente alla circonferenza nel punto {P}:

t:x=-3

ritrovando lo stesso risultato dell’esempio 3.

Osserviamo che gli esempi 2 bis e 3 bis evidenziano che le formule di sdoppiamento possono essere utilizzate senza alcuna particolare precauzione in tutti i casi, compresi quelli di rette tangenti orizzontali e verticali.

Ora, quale dei due metodi utilizzare? Il metodo che si basa sulla relazione di perpendicolarità fra rette è sicuramente quello più elegante, ed inoltre consente di risolvere il problema della retta tangente alla circonferenza in un suo punto in modo ragionato, utilizzando le conoscenze già acquisite di geometria analitica. D’altro canto, le formule di sdoppiamento non richiedono di eseguire particolari ragionamenti: basta ricordare le formule a memoria. Tuttavia, sebbene lo sforzo concettuale richiesto dalle formule di sdoppiamento sia prevalentemente mnemonico, è indubbio che tali formule consentono di acquisire familiarità con le sostituzioni. E l’abilità nelle sostituzioni e più in generale nei cambi di variabile è un requisito indispensabile per gli studi di Analisi Matematica. Inoltre, le formule di sdoppiamento come già visto non richiedono particolari ragionamenti anche nei casi di retta tangente orizzontale o verticale.

In conclusione, per quanto detto entrambi i metodi presentano i loro vantaggi e svantaggi, per cui nella scelta del metodo da utilizzare non vi resta che orientarvi secondo le vostre particolari inclinazioni, tenendo comunque sempre conto delle indicazioni fornire dal vostro insegnante e/o libro di testo.

Inoltre, come già anticipato nella lezione precedente, esiste un ulteriore metodo per la determinazione dell’equazione della retta tangente ad una circonferenza in un punto della circonferenza stessa. E tale metodo si basa sui ragionamenti fatti per la ricerca dei punti di intersezione tra una retta e una circonferenza. Per quanto quest’ultimo metodo risulti scomodo e laborioso rispetto ai due metodi sin qui illustrati nella lezione, intendiamo comunque nel seguito mostrarne l’applicazione.

Determinazione dell’equazione della retta tangente ad una circonferenza in un suo punto utilizzando l’equazione risolvente

In alternativa ai due metodi visti in precedenza, esiste un terzo metodo, anche se decisamente più scomodo, del quale per completezza ci occuperemo ora.

Riprendiamo l’esempio 1, nel quale bisognava ricercare la retta tangente alla circonferenza:

x^2+y^2+2x-4y-8=0

nel punto {P=(1,5)} appartenente alla circonferenza stessa.

L’unica cosa che sappiamo relativamente alla retta tangente cercata è che questa passa per il punto di tangenza {P}. Di conseguenza, è possibile scriverne l’equazione utilizzando la formula della retta passante per un punto ed avente coefficiente angolare {m}:

t: y-5=m(x-1)

Il problema è che per scrivere l’equazione con i valori di tutti i suoi coefficienti non conosciamo il coefficiente angolare {m}.

Tuttavia, se la retta {t} è tangente alla circonferenza, allora questa avrà con la circonferenza necessariamente un punto in comune, dato proprio dal punto di tangenza {P}. Di conseguenza, dovrà necessariamente esistere un valore del coefficiente angolare {m} per cui il sistema seguente risulterà verificato:

\begin{cases} x^2+y^2+2x-4y-8=0 \\ \\  y-5=m(x-1)\end{cases}

Infatti, il sistema è impostato per ricercare i punti di intersezione tra la circonferenza e la retta. E il sistema risulterà necessariamente determinato se {m} è il coefficiente angolare della retta tangente alla circonferenza nel punto {P}.

Anche se l’equazione della retta presenta il coefficiente angolare incognito, è comunque possibile esplicitare ad esempio la {y} nell’equazione:

\begin{cases} x^2+y^2+2x-4y-8=0 \\ \\  y=m(x-1)+5\end{cases}

ovvero, se preferite:

\begin{cases} x^2+y^2+2x-4y-8=0 \\ \\  y=mx-m+5\end{cases}

Ora, come visto nei problemi relativi all’intersezione tra una circonferenza e una retta, ciò che dobbiamo fare è sostituire l’espressione per {y} così ottenuta nell’equazione della circonferenza. In altre parole, dobbiamo sostituire ad ogni lettera {y} nell’equazione della circonferenza la quantità {mx-m+5}. Concentrandoci sulla sola equazione della circonferenza abbiamo:

x^2+\underbrace{(mx-m+5)^2}_{\substack{\text{quadrato di un}\\ \text{trinomio}}}+2x-4(mx-m+5)-8=0

Ricordando la regola del quadrato di un trinomio e sviluppando i calcoli:

\begin{align*} &x^2+m^2x^2+m^2+25-2m^2x+10mx-10m+2x-4mx+4m-20-8=0;\\ \\ & (1+m^2)x^2+(-2m^2+10m+2-4m)x+m^2+25-10m+4m-20-8=0;\\ \\ & (1+m^2)x^2+(-2m^2+6m+2)x+m^2-6m-3=0\end{align*}

L’equazione di secondo grado così ottenuta è l’equazione risolvente del sistema. Ricordando ancora quanto sappiamo relativamente al problema dell’intersezione circonferenza-retta, se il determinante dell’equazione risolvente è nullo, allora la retta è tangente alla circonferenza. Ma allora ciò che dobbiamo fare a questo punto è imporre la condizione di determinante dell’equazione risolvente nullo:

\Delta=0 \quad \Rightarrow \quad b^2-4ac=0

Nell’equazione risolvente del caso in esame, i coefficienti {a,b,c} sono funzioni del coefficiente angolare {m}:

\underbrace{ (1+m^2)}_{a}x^2+\underbrace{(-2m^2+6m+2)}_{b}x+\underbrace{m^2-6m-3}_{c}=0

Così imponendo {\Delta=0} abbiamo:

\underbrace{(-2m^2+6m+2)^2-4 \cdot (1+m^2)\cdot(m^2-6m-3)}_{b^2-4ac}=0

Svolgendo i calcoli otteniamo un’equazione di secondo grado in forma normale nella sola incognita {m}:

\begin{align*} &\cancel{4m^4}+36m^2+4-\cancel{24m^3}-8m^2+24m-4m^2+24m+12-\cancel{4m^4}+\cancel{24m^3}+12m^2=0;\\ \\ & (36-8-4+12)m^2+(24+24)m+4+12=0;\\ \\ & 36m^2+48m+16=0;\\ \\ & 9m^2+12m+4=0\end{align*}

Ora per poter scrivere in forma completa l’equazione della tangente alla circonferenza in {P} basta ricavare il coefficiente angolare {m} dall’equazione di secondo grado appena scritta. Abbiamo:

m_{1,2}=\dfrac{-\dfrac{b}{2} \pm \sqrt{\left( \dfrac{b}{2}\right)^2-ac}}{a}=\dfrac{-6\pm\sqrt{36-9 \cdot 4}}{9}=-\dfrac{2}{3}

Osserviamo che otteniamo due valori reali e coincidenti e quindi a lato pratico un solo valore per il coefficiente angolare {m}. Ciò non deve stupire, poiché effettivamente la retta tangente alla circonferenza in un punto della circonferenza stessa è unica.

Per cui sostituendo il valore di {m} appena trovato nell’equazione della retta tangente ad esempio nella forma precedentemente scritta:

y=mx-m+5

otteniamo:

y=-\dfrac{2}{3}x+\dfrac{2}{3}+5

e quindi in conclusione:

t:y=-\dfrac{2}{3}x+\dfrac{17}{3}

Abbiamo così ritrovato lo stesso risultato dell’esempio 1, anche se con calcoli molto più laboriosi. Vista quindi la lunghezza dei calcoli richiesti per quest’ultimo metodo, per la ricerca della retta tangente alla circonferenza in un suo punto consigliamo soltanto uno dei due metodi precedentemente visti.

Conclusioni

Per quanto riguarda il problema relativo a come determinare l’equazione della retta tangente ad una circonferenza in un punto appartenente alla circonferenza stessa è tutto. Nella prossima lezione ci occuperemo del problema della ricerca delle rette tangenti ad una circonferenza passanti per un punto esterno alla circonferenza stessa.

Un saluto a tutto voi e buon proseguimento con SìMatematica!