Rette tangenti ad una circonferenza per un punto esterno

 - 

Circonferenza (scuole superiori)

Le rette tangenti ad una circonferenza passanti per un punto esterno alla circonferenza stessa sono sempre due. Le equazioni di tali rette si determinano a partire dal fascio di rette proprio avente come centro il punto esterno stesso, compresa l’equazione della retta esclusa, e tenendo conto dell’equazione della circonferenza. In particolare, occorre mettere a sistema l’equazione della circonferenza in forma canonica e l’equazione del fascio, imponendo che il determinante dell’equazione risolvente corrispondente sia nullo. In tal modo è possibile ricavare in generale due valori per il coefficiente angolare, ciascuno corrispondente ad una retta tangente. Se si ottiene un solo valore del coefficiente angolare, la rimanente retta tangente sarà data dalla retta esclusa dal fascio.

Per la determinazione delle equazioni delle rette tangenti ad una circonferenza per un punto esterno ad essa, in alternativa al metodo appena indicato è anche possibile ricorrere alla formula della distanza tra una retta ed un punto. L’obiettivo è comunque sempre quello di ricavare i coefficienti angolari corrispondenti alle rette tangenti passanti per il punto esterno dato, tenendo conto eventualmente degli accorgimenti riguardanti la retta esclusa.

Sottolineiamo ancora una volta che le rette tangenti da ricercare sono sempre due, sotto l’ipotesi che il punto ove passano le tangenti sia esterno alla circonferenza. Se invece il punto appartiene alla circonferenza, come mostrato nella precedente lezione la retta tangente della quale determinare l’equazione è soltanto una (vedi: retta tangente ad una circonferenza in un suo punto).

Nel rimanente caso in cui si vogliano considerare le rette passanti per un punto interno alla circonferenza, infine, queste saranno sempre secanti alla circonferenza. Le considerazioni sin qui fatte derivano dalla geometria elementare.

Vediamo allora come determinare le equazioni delle rette tangenti ad una circonferenza passanti per un punto esterno alla circonferenza stessa, utilizzando il metodo del sistema (determinante dell’equazione risolvente nullo), e il metodo alternativo basato sulla formula della distanza punto-retta.

Come determinare le equazioni delle rette tangenti ad una circonferenza passanti per un punto ad essa esterno

Precisiamo ancora che in questa lezione ci occupiamo del caso della determinazione delle equazioni delle rette tangenti ad una circonferenza passanti per un punto esterno ad essa. Il caso più semplice relativo a come determinare l’equazione della retta tangente ad una circonferenza in un punto appartenente alla circonferenza stessa è disponibile invece nella lezione precedente.

Consideriamo una circonferenza reale non degenere {\gamma} con equazione espressa in forma canonica:

\gamma:x^2+y^2+ax+by+c=0

con {a,b,c} coefficienti reali e tali da soddisfare la relazione per la quale la circonferenza risulta reale non degenere (vedi: circonferenza).

Consideriamo un punto {P} esterno alla circonferenza, ovvero un punto tale da non appartenere né alla circonferenza, né alla regione di piano delimitata dalla circonferenza stessa. In altre parole, tale punto dovrà trovarsi “al di fuori” della circonferenza.

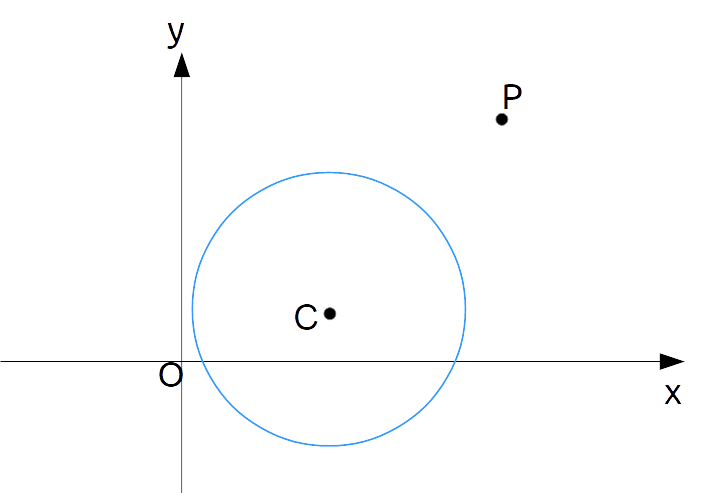
Dalla geometria elementare sappiamo che le rette tali da essere tangenti alla circonferenza e tali da passare per il punto {P} sono sempre due:

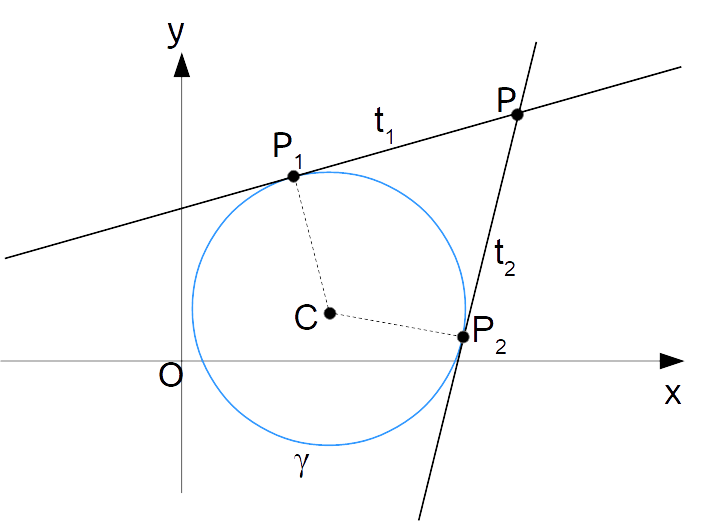
Indichiamo tali rette tangenti passanti per {P} con {t_1} e {t_2}. I punti {P_1} e {P_2} sono invece i punti appartenenti alla circonferenza nei quali le rette risultano rispettivamente tangenti alla circonferenza stessa.

Ora, a partire dall’equazione della circonferenza in forma canonica, il nostro obiettivo è determinare le equazioni delle rette tangenti {t_1} e {t_2}, passanti per il punto {P} esterno alla circonferenza.

Ciò che accomuna le due rette tangenti è il fatto che entrambe passano per il punto {P}. Così, indicato con {m} il coefficiente angolare di una qualunque delle due rette tangenti, l’equazione di ciascuna delle rette {t_1} e {t_2} dovrà essere esprimibile come:

y-y_P=m(x-x_P)

La formula utilizzata è quella relativa all’equazione di una retta passante per un punto e con coefficiente angolare noto (vedi: retta nel piano). In questo caso, tuttavia, non conosciamo ancora il valore del coefficiente angolare di ciascuna retta tangente. Ma possiamo senz’altro dire che le rette tangenti andranno ricercate sicuramente tra le rette del fascio proprio centrato nel punto {P}:

y-y_P=m(k)(x-x_P), \qquad k \in \R

Come possiamo vedere, l’equazione discende direttamente da quella precedente relativa a ciascuna delle rette tangenti, con la differenza che il coefficiente angolare è ora una funzione del parametro reale {k}.

Ora, è immediato rendersi conto che per nessun valore di {k} sarà possibile ricondurre l’equazione del fascio alla forma {x=x_P}. Ciò non è una coincidenza, in quanto la retta {x=x_P} è verticale e per le rette verticali il coefficiente angolare non è definito. Di conseguenza, il valore di {m} per cui sia possibile ritrovare a partire dall’equazione del fascio l’equazione {x=x_P} non esiste. Quindi, la retta {x=x_P} è la retta esclusa dal fascio. E nel caso in cui con i metodi che spiegheremo tra un istante si dovesse trovare un solo valore di {m}, poiché le rette tangenti da ricercare sono necessariamente due, allora la rimanente retta tangente è proprio la retta esclusa {x=x_P}.

A seguire per comodità scriveremo semplicemente {m} e non {m(k)}, lasciando sottinteso che comunque stiamo considerando un fascio di rette. E talvolta con lieve abuso di linguaggio ma per maggior chiarezza ci riferiremo a tale fascio di rette come ad una retta con coefficiente angolare indeterminato.

Metodo con sistema ed equazione risolvente

Ricordiamo che per determinare gli eventuali punti di intersezione tra una circonferenza {\gamma} ed una retta {r_1} bisogna impostare il seguente sistema (vedi: intersezioni tra una circonferenza e una retta):

\begin{cases} \gamma: x^2+y^2+ax+by+c=0 \\ \\ r_1: a_1x+b_1y+c_1=0\end{cases}

Nel nostro caso, l’idea è quella di impostare il sistema relativo alla ricerca dei punti di intersezione tra la circonferenza data e l’equazione di una generica retta ad essa tangente, fra quelle del fascio scritto in precedenza:

\begin{cases} \gamma: x^2+y^2+ax+by+c=0 \\ \\y-y_P=m(x-x_P)\end{cases}

Il nostro obiettivo è determinare i due valori del coefficiente angolare {m} corrispondenti alla due rette tangenti passanti per il punto esterno {P}, o almeno uno dei due nel caso in cui una delle due rette tangenti sia verticale.

L’idea è quella anzitutto di esplicitare la variabile {y} dall’equazione della generica retta tangente:

\begin{cases} \gamma: x^2+y^2+ax+by+c=0 \\ \\y=m(x-x_P)+y_P \quad \rightarrow \quad y=mx-mx_P+y_P\end{cases}

e quindi sostituire l’espressione appena ottenuta per {y} nell’equazione della circonferenza:

\begin{cases} \gamma: x^2+\left( mx-mx_P+y_P\right)^2+ax+b(mx-mx_P+y_P)+c=0 \\ \\ y=mx-mx_P+y_P\end{cases}

Sviluppando i calcoli relativamente alla prima equazione a sistema, è possibile ottenere caso per caso un’equazione risolvente nelle due incognite {x} e {m}. In particolare, si tratta più propriamente di un’equazione di secondo grado nell’incognita {x} e con coefficienti dei suoi termini dipendenti da {m}.

Ora, poiché richiediamo che la retta a sistema sia tangente alla circonferenza, il determinante dell’equazione risolvente dovrà essere necessariamente nullo. Così, poiché i coefficienti dei termini dell’equazioni sono funzioni di {m}, imponendo la condizione di determinante nullo si otterrà un’equazione di secondo grado nella sola incognita {m}. E quest’ultima, una volta risolta, fornirà i valori dei coefficienti angolari delle rette tangenti alla circonferenza e tali da passare per il punto {P} dato. Si otterrà un solo valore di {m} nel solo caso in cui una delle due rette tangenti, come già anticipato, sia verticale.

Infine, per eseguire i calcoli è necessario ricordare la regola del quadrato di un trinomio.

Esempio 1

Determinare le equazioni delle rette {t_1} e {t_2} tangenti alla circonferenza {\gamma: x^2+y^2-2x-2y+1=0} e passanti per il punto {P=(1,3)} esterno alla circonferenza stessa.

Le rette tangenti {t_1} e {t_2} vanno ricercate nel fascio proprio di rette centrato nel punto {P=(1,3)}, compresa la retta esclusa. Tale fascio ha equazione:

y-y_P=m(x-x_P)

ovvero, sostituendo i valori delle coordinate del punto {P}:

y-3=m(x-1)

Attenzione a non scambiare tra loro l’ascissa e l’ordinata del punto {P}.

Ora, considerata l’equazione della circonferenza in esame, il sistema da impostare è il seguente:

\begin{cases}x^2+y^2-2x-2y+1=0 \\ \\ y-3=m(x-1)\end{cases}

Esplicitiamo la variabile {y} dalla seconda equazione a sistema:

\begin{cases}x^2+y^2-2x-2y+1=0 \\ \\ y=\boxed{mx-m+3} \end{cases}

A questo punto consideriamo la sola equazione della circonferenza, e sostituiamo a ciascuna lettera {y} in essa presente l’espressione evidenziata nel riquadro. In tal modo, ci liberiamo dalla variabile {y} e riconduciamo l’equazione della circonferenza ad un’equazione che conterrà soltanto termini in {x} ed in {m}:

x^2+\left( mx-m+3\right)^2-2x-2\left( mx-m+3\right)+1=0

Sviluppando i calcoli al primo membro:

\small \begin{align*} &x^2+m^2x^2+m^2+9-2m^2x+6mx-6m-2x-2mx+2m-6+1=0; \\ \\ & (1+m^2)x^2+(-2m^2+6m-2-2m)x+m^2+9-6m+2m-6+1=0;\\ \\ & \underbrace{(1+m^2)}_{a}x^2+\underbrace{(-2m^2+4m-2)}_{b}x+\underbrace{m^2-4m+4}_{c}=0\end{align*}

Come evidenziato abbiamo ottenuto un’equazione di secondo grado nella forma normale {ax^2+bx+c=0} con coefficienti {a,b,c} dipendenti da {m}. Questa è l’equazione risolvente del sistema.

La condizione di determinante nullo, che corrisponde al fatto che ricerchiamo le rette tangenti alla circonferenza, si scrive come:

\underbrace{b^2-4ac}_{\Delta}=0

e quindi nel nostro caso (anche se sarebbe possibile utilizzare il {\Delta/4)}):

\begin{align*} &(-2m^2+4m-2)^2-4 \cdot (1+m^2)\cdot(m^2-4m+4)=0\end{align*}

Svolgendo i calcoli (serve ancora il quadrato di un trinomio):

\small \begin{align*} &\cancel{4m^4}+\cancel{16m^2}+4-\cancel{16m^3}+8m^2-\cancel{16m}-4m^2+\cancel{16m}-16-\cancel{4m^4}+\cancel{16m^3}-\cancel{16m^2}=0;\\ \\ &4m^2-12=0 \quad \Rightarrow  \quad m^2=3 \quad \Rightarrow \quad m_{1,2}=\pm \sqrt{3}\end{align*}

Abbiamo così ottenuto per il coefficiente angolare {m} i due valori {\sqrt{3}} e {-\sqrt{3}}, ai quali corrispondono le due rette tangenti cercate. Per determinarne le equazioni, basta riprendere l’equazione della retta tangente nel sistema e sostituire i due valori di {m}:

\begin{align*} & t : y={mx-m+3}  \quad \text{con}  \quad m=\sqrt{3} \quad \Rightarrow t_1: y= \sqrt{3}x-\sqrt{3}+3; \\ \\ & t:y=mx-m+3 \quad \text{con} \quad m=-\sqrt{3} \quad \Rightarrow  t_2: y=-\sqrt{3}x+\sqrt{3}+3  \end{align*}

Siamo così riusciti a scrivere le equazioni delle due rette tangenti alla circonferenza e passanti per il punto {P=(1,3)}.

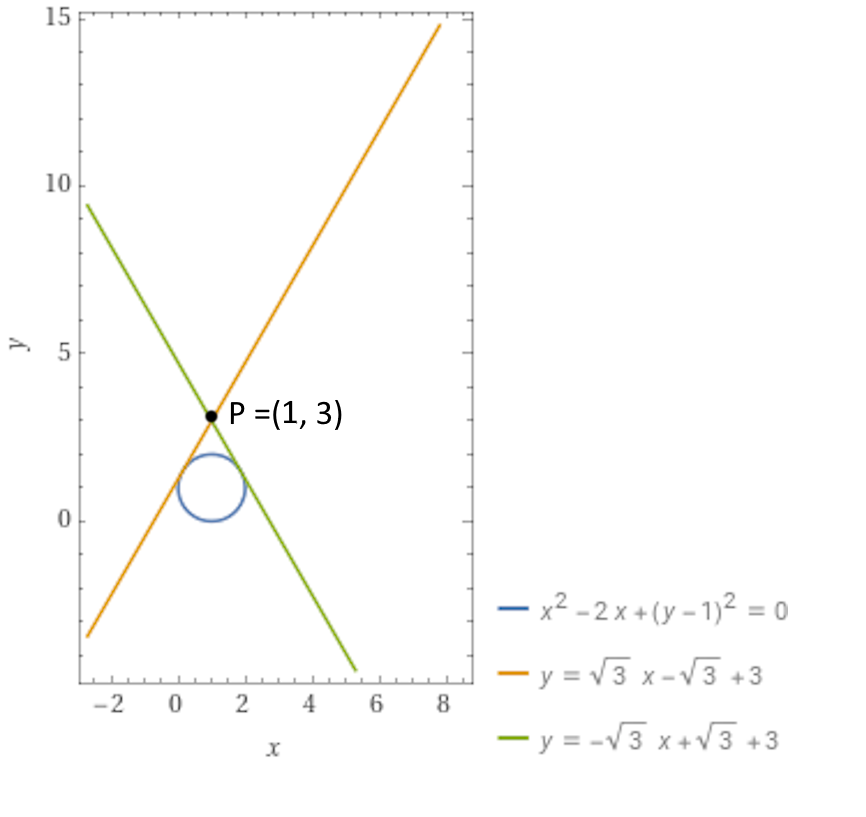
Per meglio comprendere la logica che sta dietro alla procedura seguita, riprendiamo quanto sappiamo sull’intersezione fra una retta e una circonferenza. L’idea per ricercare i punti di intersezione (eventuali) tra una circonferenza e una retta è quella di ricercare quei punti che soddisfano contemporaneamente le condizioni di appartenenza sia alla circonferenza, sia alla retta. E ciò corrisponde ad impostare un sistema ove siano presenti le equazioni della retta e della circonferenza. Infatti, le eventuali soluzioni del sistema saranno le coppie di valori che corrispondono alle coordinate dei punti di intersezione tra la circonferenza e la retta:

\begin{cases} x^2+y^2+ax+by+c=0 \\ \\ a_1x+b_1y+c=0\end{cases}

E la retta sarà in particolare tangente alla circonferenza se il determinante dell’equazione risolvente il sistema è nullo.

Ora, nel ricercare le rette tangenti alla circonferenza passanti per un dato punto esterno, quello che facciamo è mettere a sistema l’equazione di una “generica” retta passante per il punto esterno stesso:

\begin{cases} x^2+y^2+ax+by+c=0 \\ \\y-y_P=m(x-x_P)\end{cases}

Che la retta sia “generica” lo si riconosce dal fatto che il valore del coefficiente angolare {m} è sconosciuto.

Quindi ciò che desideriamo è imporre una condizione che consenta di ricavare il valore o i valori di {m} corrispondenti alle rette tangenti. Ma come sappiamo, tale condizione equivale a richiedere che il determinante dell’equazione risolvente sia uguale a zero. Per cui il valore o i valori di {m} tali da soddisfare tale condizione corrisponderanno alle rette tangenti cercate.

E ricordiamo ancora che se dovesse capitare di trovare un solo valore per {m}, la retta tangente mancante è quella esclusa dal fascio, ovvero la retta verticale {x=x_P}. Ma vediamo questo particolare caso nell’esempio immediatamente a seguire.

Esempio 2

Determinare le equazioni delle rette tangenti alla circonferenza {\gamma: x^2+y^2+6x=0} e passanti per il punto esterno alla circonferenza {P=(-6,4)}.

Le rette tangenti andranno ricercate fra le rette del fascio proprio centrato nel punto {P}, ovvero:

y-4=m[x-(-6)]

e quindi:

y-4=m(x+6)

Così dobbiamo impostare il sistema:

\begin{cases} x^2+y^2+6x=0 \\ \\ y-4=m(x+6)\end{cases}

ovvero, esplicitando la {y} nella seconda equazione:

\begin{cases} x^2+y^2+6x=0 \\ \\ y=m(x+6)+4 \quad \rightarrow \quad y=mx+6m+4\end{cases}

A questo punto consideriamo la sola equazione della circonferenza, e sostituiamo in essa alla lettera {y} l’espressione {mx+6m+4}:

\begin{align*} &x^2+(mx+6m+4)^2+6x=0;\\ \\ & x^2+m^2x^2+36m^2+16+12m^2x+8mx+48m+6x=0;\\ \\ & \underbrace{(1+m^2)}_{a}x^2+\underbrace{(12m^2+8m+6)}_{b}x+\underbrace{36m^2+48m+16}_{c}=0;\end{align*}

Imponiamo il determinante dell’equazione di secondo grado appena scritta uguale a zero. Utilizziamo in questo caso per comodità il {\dfrac{\Delta}{4}}:

\left( \dfrac{b}{2}\right)^2-ac =0

Ciò è conveniente dato che i coefficienti che figurano nella quantità {b} sono tutti pari. Abbiamo:

\small \begin{align*} &(6m^2+4m+3)^2-(1+m^2) \cdot (36m^2+48m+16)=0; \\ \\ & \cancel{36m^4}+\cancel{16m^2}+9+\cancel{48m^3}+\cancel{36m^2}+24m-\cancel{36m^2}-48m-16-\cancel{36m^4}-\cancel{48m^3}-\cancel{16m^2}=0;\\ \\&-24m-7=0 \quad \Rightarrow \quad m=-\dfrac{7}{24} & \end{align*}

Osserviamo che abbiamo ottenuto un solo valore per {m}. Ma ciò, attenzione, non significa che la retta tangente alla circonferenza e passante per {P} sia soltanto una! Ricordiamo infatti che le rette tangenti ad una circonferenza e passanti per un punto esterno ad essa sono sempre due. Ed infatti, nel nostro caso la retta tangente mancante è quella che corrisponde alla retta esclusa dal fascio di rette di equazione {y-4=m(x+6)}, ovvero la retta {x=-6} (la retta verticale passante per {P}).

Così in conclusione abbiamo la retta tangente {t_1} corrispondente al valore {-\dfrac{7}{24}} del coefficiente angolare, e la retta {t_2} di equazione {x=-6} che corrisponde alla retta esclusa dal fascio. Come nell’esempio precedente, per determinare l’equazione della retta {t_1} basta sostituire il valore di {m} ricavato nell’equazione del fascio, ad esempio nella forma {y=mx+6m+4}. Abbiamo quindi per le rette tangenti cercate le equazioni:

\begin{align*} &y=-\dfrac{7}{24}x+6 \cdot \left( -\dfrac{7}{24} \right)+4  \quad \Rightarrow t_1: y=-\dfrac{7}{24}x+\dfrac{9}{4}; \\ \\ &t_2: x=-6 \end{align*}

Come scrivere le equazioni delle rette tangenti ad una circonferenza utilizzando la formula della distanza punto-retta

Un altro metodo per la determinazione delle rette tangenti ad una circonferenza passanti per un punto esterno ad essa si basa sull’utilizzo della formula per la distanza punto-retta.

Consideriamo una circonferenza di centro {C=(x_C, y_C)} e raggio {r} con le rette ad essa tangenti per il punto esterno {P=(x_P, y_P)}:

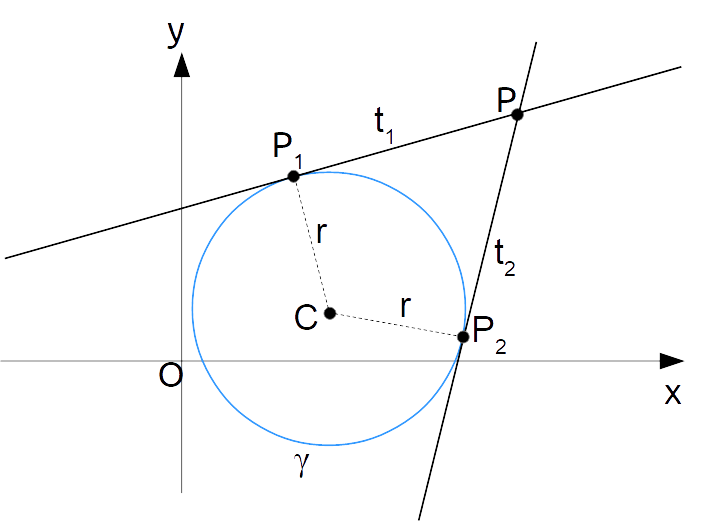
Le rette tangenti {t_1} e {t_2} sono da ricercare fra le rette del fascio proprio centrato in {P} di equazione:

y-y_P=m(x-x_P)

ovvero:

y=mx-mx_P+y_P 

Poiché l’equazione è della forma {y=mx+q}, deduciamo:

q=-mx_P+y_P

Non dimentichiamo inoltre che tra le possibili rette tangenti deve anche essere compresa la retta esclusa {x=x_P}.

Ora, è evidente dalla figura che per la definizione di raggio di una circonferenza devono necessariamente valere le uguaglianze:

\overline{CP_1}=r; \qquad \overline{CP_2}=r

Ma {\overline{CP_1}} è la distanza fra la retta {t_1} e il punto {C}, ed allo stesso modo {\overline{CP_2}} è la distanza fra la retta {t_2} ed lo stesso punto {C}. Di conseguenza le precedenti uguaglianze si possono riscrivere come:

d(C, t_1)=r; \qquad d(C, t_2)=r \qquad (*)

Ricordiamo la formula per il calcolo della distanza punto-retta nel piano, con equazione della retta in forma esplicita, formula che nel nostro caso può essere espressa come:

{d(C,r)=\dfrac{|y_C-(mx_C+q)|}{\sqrt{1+m^2}}} \qquad (@)

Di conseguenza, tenendo conto dell’equazione del fascio proprio di rette con centro in {P}, dalle uguaglianze * discende la seguente uguaglianza:

\dfrac{|y_C-(mx_C-\overbrace{mx_P+y_P}^{q})|}{\sqrt{1+m^2}}=r \qquad (**)

Tale equazione consente in generale di ricavare entrambi i coefficienti angolari delle rette {t_1} e {t_2}. Nel caso particolare in cui l’equazione fornisca un solo valore per {m}, allora l’altra retta tangente sarà la retta {x=x_P} esclusa dal fascio.

Esempio 3

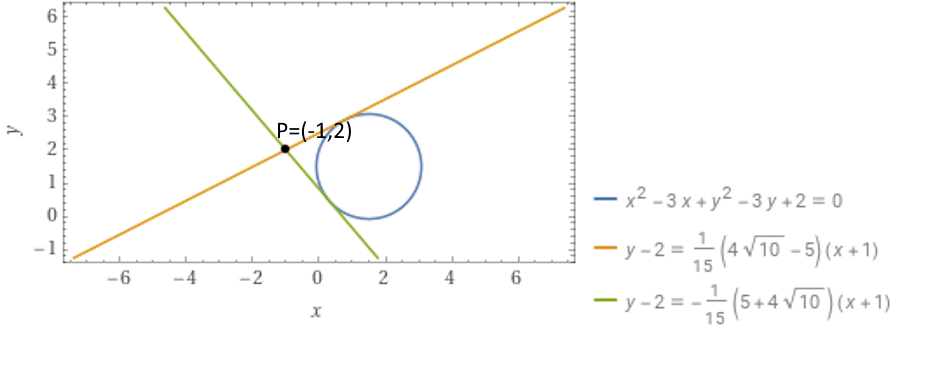
Scrivere le equazioni delle rette {t_1} e {t_2} tangenti alla circonferenza di equazione {x^2+y^2-3x-3y+2=0} e tali da passare per il punto esterno {P=(-1,2)}.

Cominciamo con il calcolare il centro e il raggio della circonferenza, dati necessari per impostare l’equazione **. Abbiamo:

\begin{align*} & x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot (-3)=\dfrac{3}{2}; \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot (-3)=\dfrac{3}{2} \\ \\ &r=\sqrt{x_C^2+y_C^2-c}=\sqrt{\dfrac{9}{4}+\dfrac{9}{4}-2} =\sqrt{\dfrac{5}{2}}=\dfrac{\sqrt{5}}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{\sqrt{10}}{2}\end{align*}

Osserviamo che per semplificare la misura del raggio siamo ricorsi alla razionalizzazione.

Ora, ricordare l’equazione ** è piuttosto scomodo, per cui conviene seguire i ragionamenti passo passo.

Le rette tangenti {t_1} e {t_2} sono da ricercare nel fascio proprio di centro {P}:

y-y_P=m(x-x_P)

ovvero:

y=mx-mx_P+y_P

L’equazione del fascio può essere riletta come l’equazione in forma esplicita di una retta con coefficiente angolare {m} indeterminato, ovvero un’equazione della forma {y=mx+q}, avente ordinata all’origine {q=-mx_P+y_P}.

Ricordando la formula per la distanza punto-retta nella forma @ abbiamo nel nostro caso:

{d(C,r)=\dfrac{|y_C-(mx_C+q)|}{\sqrt{1+m^2}}} =\dfrac{|y_C-(mx_C-mx_P+y_P)|}{\sqrt{1+m^2}}

e poiché per definizione la distanza tra la retta {r} e il punto {C} è uguale al raggio {r} della circonferenza:

\dfrac{|y_C-(mx_C-mx_P+y_P)|}{\sqrt{1+m^2}}=r

Sostituendo i valori delle coordinate dei punti {C} e {P} e del raggio {r}, otteniamo la seguente equazione nell’incognita {m}:

\dfrac{\left| \dfrac{3}{2}-\left[ \dfrac{3}{2}m-(-1)\cdot m+2\right] \right|}{\sqrt{1+m^2}}=\dfrac{\sqrt{10}}{2}

Eseguendo i calcoli al primo membro abbiamo:

\begin{align*} &\dfrac{\left|\dfrac{3}{2}-\left(\dfrac{3}{2}m+m+2 \right)\right|}{\sqrt{1+m^2}}=\dfrac{\sqrt{10}}{2}; \\ \\ & \dfrac{\left|{\dfrac{3}{2}}-{\dfrac{3}{2}}m-m-2\right|}{\sqrt{1+m^2}}=\dfrac{\sqrt{10}}{2};\\ \\ & \dfrac{\left|-\dfrac{5}{2}m-\dfrac{1}{2}\right|}{\sqrt{1+m^2}}=\dfrac{\sqrt{10}}{2} \end{align*}

Ora spostiamo tutto al primo membro e mettiamo tutti i termini a denominatore comune:

\begin{align*} &\dfrac{\left|-\dfrac{5}{2}m-\dfrac{1}{2}\right|}{\sqrt{1+m^2}}-\dfrac{\sqrt{10}}{2}=0;\\ \\ & \dfrac{\left|\dfrac{1}{2}(-5m-1)\right|}{\sqrt{1+m^2}}-\dfrac{\sqrt{10}}{2}=0;\\ \\ & \dfrac{\left|-5m-1\right|}{2\sqrt{1+m^2}}-\dfrac{\sqrt{10}}{2}=0;\\ \\ & \dfrac{\left|-5m-1\right|-\sqrt{10}\sqrt{1+m^2}}{2\sqrt{1+m^2}}=0\end{align*}

A questo punto è possibile eliminare il denominatore senza alcuna discussione. Infatti, il radicando {1+m^2} è una quantità sempre positiva non nulla. Di conseguenza, il radicale {\sqrt{1+m^2}} esisterà per ogni valore di {m} e il denominatore della frazione algebrica al primo membro non sarà mai nullo.

\left|-5m-1\right|-\sqrt{10}\sqrt{1+m^2}=0

Ora, riscriviamo l’equazione come segue, separando le quantità in valore assoluto da quelle sotto radice:

|-5m-1|=\sqrt{10}\sqrt{1+m^2}

ovvero, tenendo conto che al secondo membro abbiamo un prodotto fra radicali con lo stesso indice:

|-5m-1|=\sqrt{10(1+m^2)}

Abbiamo così ottenuto un’equazione irrazionale con valori assoluti, che tuttavia è di risoluzione agevole.

In particolare, è possibile elevare entrambi i membri al quadrato, senza dover imporre alcuna condizione di concordanza. Infatti, entrambi i membri sono positivi, in quanto rispettivamente valore assoluto e radice quadrata. Inoltre, non dobbiamo nemmeno imporre alcuna condizione di realtà dei radicali (il radicando al secondo membro è sempre positivo). Abbiamo quindi:

(-5m-1)^2=10(1+m^2)

Sviluppiamo i calcoli e risolviamo l’equazione rispetto a {m}:

\begin{align*} & 25m^2+10m+1-10-10m^2=0;\\ \\ & 15m^2+10m-9=0 \end{align*}

Otteniamo un’equazione di secondo grado nell’incognita {m}, che risolta fornisce:

\begin{align*} &m_{1,2} = \dfrac{-\dfrac{b}{2}\pm \sqrt{\left(\dfrac{b}{2}\right)^2-ac}}{a}=\dfrac{-5\pm \sqrt{25-15 \cdot (-9)}}{15}=\\ \\ & =\dfrac{-5 \pm \sqrt{25+135}}{15}=\dfrac{-5 \pm \sqrt{160}}{15}=\dfrac{-5 \pm \sqrt{5 \cdot 2 \cdot 2^4}}{15}=\\ \\ & =\dfrac{-5 \pm 4\sqrt{5 \cdot 2 }}{15}=\dfrac{-5 \pm 4\sqrt{10}}{15}=\begin{cases} \dfrac{-5+4\sqrt{10}}{15} \\ \\ \dfrac{-5-4\sqrt{10}}{15}\end{cases}\end{align*}

Abbiamo così ottenuto i valori dei due coefficienti angolari {m_1} ed {m_2} corrispondenti alla rette tangenti {t_1} e {t_2}. L’equazione di ciascuna retta tangente si ottiene poi sostituendo ciascuno dei due valori nell’equazione precedentemente scritta:

y-y_P=m(x-x_P)

Riusciamo a scrivere in questo modo le due equazioni cercate:

t_1: y-2= \dfrac{-5+4\sqrt{10}}{15} (x+1); \qquad t_2:y-2= \dfrac{-5-4\sqrt{10}}{15}(x+1)

Non conviene in questo caso ricondurre le equazioni alla forma esplicita {y=mx+q}, per cui l’esercizio è così concluso.

Vediamo ora un ulteriore esempio su come scrivere le equazioni delle rette tangenti ad una circonferenza e passanti per un punto esterno ad essa.

Esempio 4

Scrivere le equazioni delle rette {t_1} e {t_2} tangenti alla circonferenza di equazione {x^2+y^2-4x+6y-12=0} e passanti per il punto esterno P=(-5,2).

Determiniamo centro e raggio della circonferenza:

\begin{align*} &x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot (-4)=2; \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot 6=-3 \\ \\ &r=\sqrt{x_C^2+y_C^2-c}=\sqrt{2^2+(-3)^2-(-12)}=\sqrt{4+9+12}=5\end{align*}

Imponiamo che la distanza fra ciascuna delle rette {r_1} ed {r_2} sia uguale al raggio {r} della circonferenza, utilizzando per brevità direttamente la **:

\dfrac{|y_C-(mx_C-mx_P+y_P)|}{\sqrt{1+m^2}}=r

Sostituendo i valori abbiamo nel nostro caso:

\dfrac{|-3-(2m-(-5)m+2)|}{\sqrt{1+m^2}}=5

Sviluppando i calcoli otteniamo:

\begin{align*} &\dfrac{|-3-(2m+5m+2)|}{\sqrt{1+m^2}} =5; \\ \\ &  \dfrac{|-5-7m|}{\sqrt{1+m^2}}=5; \\ \\ & \dfrac{|-5-7m|-5\sqrt{1+m^2}}{\cancel{\sqrt{1+m^2}}}=0; \\ \\ & |-5-7m|= 5\sqrt{1+m^2}; \\ \\ & (-5-7m)^2=25(1+m^2);\\ \\ & \cancel{25}+49m^2+70m-\cancel{25}-25m^2=0;\\ \\ & 24m^2+70m=0; \\ \\ & 12m^2+35m=0;\\ \\ & m(12m+35)=0 \qquad \Rightarrow \qquad m=0 \quad \vee \quad m= -\dfrac{35}{12}\end{align*}

L’equazione di secondo grado in {m} che abbiamo appena risolto è spuria, ed abbiamo in particolare utilizzato un raccoglimento per {m} seguito dall’applicazione della legge di annullamento del prodotto.

Ora, come ormai sappiamo le rette tangenti cercate appartengono necessariamente al fascio:

y-y_P=m(x-x_P)

compresa eventualmente la retta esclusa {x=x_P}. Nel nostro caso abbiamo due valori per {m}, che sostituiti nell’equazione del fascio forniscono rispettivamente:

\begin{align*} &y-2=0 \cdot (x+5) \quad \Rightarrow \quad t_1: y = 2; \\ \\ & y-2=-\dfrac{35}{12} \cdot (x+5) \quad \Rightarrow \quad t_2: y=-\dfrac{35}{12}x-\dfrac{151}{12}\end{align*}

Queste sono in conclusione le equazioni delle rette tangenti alla circonferenza nel punto {P} ad essa esterno.

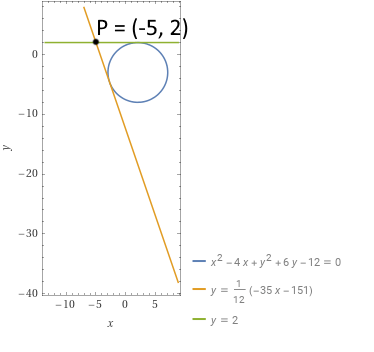
Osserviamo che abbiamo ottenuto tranquillamente fra le rette tangenti alla circonferenza passanti per {P} una retta orizzontale, poiché questa è compresa nel fascio (si ricade in una retta orizzontale per {m=0}).

Conclusioni

Per quanto riguarda come determinare le equazioni delle rette tangenti ad una circonferenza passanti per un punto esterno ad essa è tutto. Nel corso della lezione abbiamo presentato due differenti metodi. In particolare abbiamo visto:

• come determinare le equazioni delle rette tangenti ad una circonferenza passanti per un punto esterno {P}, utilizzando il metodo del sistema risolvente;
• come determinare le equazioni di tali rette utilizzando il metodo basato sulla formula della distanza punto-retta.

Quale dei due metodi utilizzare? Come sempre, il consiglio è quello di regolarvi in base alle indicazioni del vostro insegnante e/o libro di testo. Tuttavia, personalmente ci sentiamo di consigliare il metodo che fa uso della formula della distanza punto-retta, poiché è quello che più consente di utilizzare le conoscenze sin qui acquisite sulla geometria analitica. In ogni caso, il metodo del sistema risolvente è comunque utilizzabile tranquillamente, e tra l’altro non richiede di ricordare la formula della distanza punto-retta. Presenta comunque lo svantaggio di richiedere dei calcoli un po’ più pesanti, e in particolare è necessario ricordare la regola del quadrato di un trinomio.

Un punto in comune ai due metodi, come abbiamo visto, è dato dalla necessità di ricordare l’equazione di un fascio proprio di rette, nella particolare forma:

y-y_P=m(x-x_P)

ove il centro del fascio {P=(x_P, y_P)} è un punto esterno alla circonferenza data, punto in comune alla due rette tangenti {t_1} e {t_2}. Ricordiamo sempre, infine, che la retta esclusa al fascio ha equazione {x=x_P}.

Nel salutarci, vi segnaliamo la seguente risposta sulle rette condotte da un punto tangenti a una circonferenza, utile per chi vuole allenarsi con un ulteriore esercizio. Un saluto a tutti voi e buon proseguimento con SìMatematica!