Condizioni per determinare l’equazione di una circonferenza

 - 

Circonferenza (scuole superiori)

Studiare le condizioni per determinare l’equazione di una circonferenza nel piano corrisponde a comprendere sotto quali ipotesi una circonferenza del piano risulta univocamente determinata. In altre parole, ci chiediamo quali sono i dati necessari e sufficienti affinché sia possibile scrivere l’equazione di una circonferenza.

Al fine di individuare le condizioni necessarie e sufficienti per determinare l’equazione di una circonferenza sono di aiuto noti teoremi della geometria euclidea. In questa lezione non ci occuperemo di trattare approfonditamente tali teoremi, ma piuttosto cercheremo di formalizzare dette condizioni grazie all’ausilio della geometria analitica. Così il nostro obiettivo è quello di scrivere l’equazione di una circonferenza a partire da opportuni dati di partenza, utilizzando le conoscenze sin qui acquisite.

Vedremo in particolare:

• come scrivere l’equazione di una circonferenza a partire dalle coordinate di tre suoi punti (circonferenza per tre punti non allineati);
• come scrivere l’equazione di una circonferenza noti un suo punto e le coordinate del suo centro;
• ancora, come determinare l’equazione di una circonferenza a partire dalle coordinate di due punti appartenenti ad essa e dall’equazione di una retta passante per il centro della circonferenza stessa;
• infine, come scrivere l’equazione della circonferenza conoscendo le coordinate del centro e posta la condizione di tangenza ad una determinata retta. In altre parole, vedremo come determinare l’equazione di una circonferenza avente centro noto e tale da essere tangente ad una retta della quale è data l’equazione.

Prima di iniziare, precisiamo che con il termine di condizioni “necessarie e sufficienti” intendiamo in questo contesto quelle condizioni che servono e allo stesso tempo bastano per scrivere l’equazione della circonferenza. Ad esempio, se per scrivere l’equazione di una data circonferenza ci venissero fornite le coordinate di quattro punti, è evidente per quanto detto che le coordinate del quarto punto sarebbero di troppo. L’idea è allora quella di avere il numero minimo di condizioni necessarie per scrivere l’equazione della circonferenza. Ciò permette l’impostazione di un metodo risolutivo del problema che non sia inutilmente oneroso.

Ricordiamo infine, come caso banale, che una circonferenza del piano è univocamente determinata una volta note le coordinate del suo centro e la misura del suo raggio. Ciò è diretta conseguenza di quanto abbiamo visto a suo tempo sull’equazione della circonferenza. Così, una volta note le coordinate del centro e la misura del raggio è sempre possibile scrivere l’equazione della circonferenza corrispondente.

Condizioni necessarie e sufficienti per determinare l’equazione di una circonferenza nel piano cartesiano

Coordinate di tre punti della circonferenza (passaggio della circonferenza per tre punti)

Siano dati tre punti del piano cartesiano non allineati tra loro. Ricordiamo che tre punti sono non allineati tra loro se, considerata la retta che passa ad esempio per i primi due punti, risulta che il terzo punto non appartiene a tale retta.

Dal punto di vista della geometria analitica, precisiamo che la verifica del non allineamento di tre punti consiste nello scrivere l’equazione della retta passante ad esempio per i primi due punti, e quindi verificare che le coordinate del terzo punto non soddisfano la condizione di appartenenza della retta stessa (vedi: circonferenza).

Ora, dati tre punti del piano non allineati tra loro esiste sempre ed è unica la circonferenza che passa per essi. In altre parole, esiste sempre un’unica circonferenza tale che ciascuno dei tre punti dati appartiene ad essa.

Per dimostrare tale affermazione, dimentichiamo per un attimo la circonferenza e consideriamo i segmenti che congiungono tra loro ad esempio i punti {P_1} e {P_2} e i punti {P_2} e {P_3}. Tracciamo inoltre gli assi di tali segmenti, che indicheremo rispettivamente con {r_1} ed {r_2}:

Ricordiamo che l’asse di un segmento è una retta perpendicolare al segmento e tale da passare per il punto medio del segmento stesso. Inoltre, l’asse è formato da punti aventi tutti la medesima distanza dagli estremi del segmento.

L’intersezione tra i due assi {r_1} ed {r_2} è data dal punto {C} indicato in figura. E poiché tale punto appartiene all’asse {r_1}, è sicuramente equidistante dai punti {P_1} e {P_2}, estremi del segmento {\overline{P_1P_2}}. Ma dato che il punto {C} appartiene anche all’asse {r_2}, tale punto sarà pure equidistante dai punti {P_2} e {P_3}, estremi del segmento {\overline{P_2P_3}}

Dal ragionamento fatto segue che le misure delle seguenti distanze sono tutte uguali fra loro. Indichiamo la misura corrispondente a tali distanze con {r}:

\overline{P_1C}=\overline{P_2C}=\overline{P_3C}=r

Di conseguenza i punti {P_1}, {P_2} e {P_3} hanno tutti la stessa distanza {r} dal punto {C}. E poiché la circonferenza è definita come il luogo geometrico di punti tutti equidistanti dal centro, concludiamo che per i punti {P_1}, {P_2} e {P_3} passa la circonferenza di centro {C} e raggio {r}:

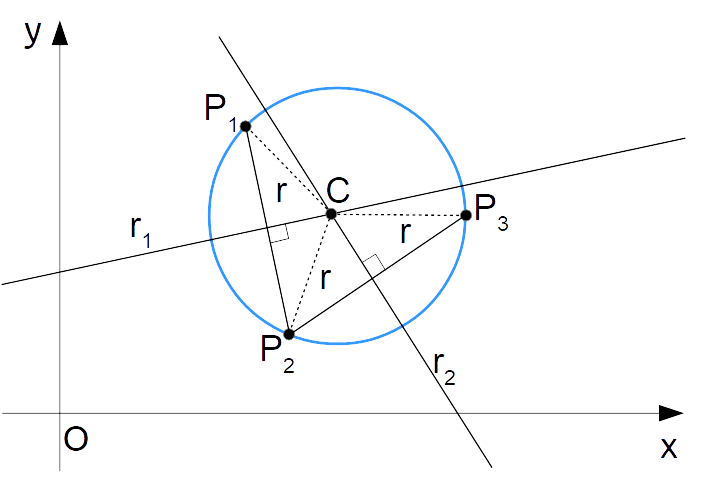
La semplice dimostrazione proposta delinea anche una possibile procedura per determinare l’equazione di una circonferenza a partire dalle coordinate di tre suoi punti. Dati i tre punti non allineati {P_1, \: P_2} e {P_3} basterà infatti scrivere le equazioni degli assi relativi ai segmenti {\overline{P_1P_2}} e {\overline{P_2P_3}}, per poi mettere tali equazioni a sistema. Il risultato saranno le coordinate del centro {C} della circonferenza, ottenute dall’intersezione dei due assi. A tal punto, calcolando la distanza fra il centro {C} ed uno a scelta dei punti dati si otterrà la misura del raggio. Ed infine, note le coordinate del centro e la misura del raggio, sarà possibile scrivere l’equazione della circonferenza.

Esempio 1 (circonferenza per tre punti ricercando il centro e il raggio)

Scrivere l’equazione della circonferenza passante per i punti non allineati fra loro {P_1=(2,0)}, {P_2=(3,1)} e {P_3=(-1,1)}.

Cominciamo scrivendo le equazioni delle rette {s_1} ed {s_2} che passano rispettivamente per i due punti {P_1} e {P_2} e per i due punti {P_2} e {P_3}. Osserviamo che tali rette sono parallele ai segmenti {\overline{P_1P_2}} e {\overline{P_2P_3}}.

Ricordiamo anzitutto la formula della retta per due punti del piano:

\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}

Per la retta {s_1} passante per i due punti {P_1=(2,0)} e {P_2=(3,1)} abbiamo:

\dfrac{y-0}{1-0}=\dfrac{x-2}{3-2} \quad \Rightarrow \quad s_1: y=x-2 \quad \Rightarrow \quad m_1=1

ove {m_1} è il coefficiente angolare della retta {s_1}.

In alternativa, osserviamo che avremmo anche potuto direttamente utilizzare la formula per il calcolo del coefficiente angolare.

Per la retta {s_2} passante per i punti {P_2=(3,1)} e {P_3=(-1,1)} non è possibile utilizzare la formula appena vista. Infatti, i due punti sono allineati orizzontalmente (condividono la stessa ordinata). Ma poiché dei punti che hanno la stessa ordinata appartengono ad una retta orizzontale, e poiché l’ordinata in comune ai punti è {1}, per l’equazione di {s_2} possiamo scrivere:

s_2: y=1 \quad \Rightarrow \quad m_2=0

Ora, dato che i segmenti {\overline{P_1P_2}} e {\overline{P_2P_3}} appartengono alle rette {s_1} ed {s_2}, le rette perpendicolari a {s_1} ed {s_2} e passanti per i punti medi dei segmenti saranno rispettivamente gli assi {r_1} ed {r_2} di tali segmenti.

Calcoliamo i punti medi dei segmenti:

\begin{align*} & M_1=\left( \dfrac{x_{P_1}+x_{P_2}}{2}, \dfrac{y_{P_1}+y_{P_2}}{2}\right)=\left( \dfrac{2+3}{2}, \dfrac{0+1}{2}\right)=\left( \dfrac{5}{2}, \dfrac{1}{2}\right) \\ \\ & M_2=\left( \dfrac{x_{P_2}+x_{P_3}}{2}, \dfrac{y_{P_2}+y_{P_3}}{2}\right) =\left( \dfrac{3-1}{2}, \dfrac{1+1}{2}\right)=(1,1)\end{align*}

Così, a partire dal valore del coefficiente angolare della retta {s_1}, ricordando quanto sappiamo sulla relazione di perpendicolarità fra rette e ricordando inoltre l’equazione di una retta passante per un punto con coefficiente angolare noto possiamo scrivere:

\begin{align*} &r_1: y-y_{M_1} = -\dfrac{1}{m_1}(x-x_{M_1}) \quad \Rightarrow r_1: y-\dfrac{1}{2}=-1\left( x-\dfrac{5}{2}\right) \end{align*}

ovvero:

r_1:y=-x+\dfrac{5}{2}+\dfrac{1}{2} \quad \Rightarrow \quad r_1: y=-x+3

In pratica abbiamo scritto l’equazione dell’asse {r_1} intendendo questo come la retta che passa per il punto {M_1} ed avente coefficiente angolare {-\dfrac{1}{m_1}} (infatti la retta {r_1} è perpendicolare alla retta {s_1} avente coefficiente angolare {m_1}).

Per la retta {r_2}, a partire dall’equazione della retta {s_2} basta ricordare che una retta perpendicolare ad una retta orizzontale è necessariamente verticale. Ed inoltre, se la retta passa per {M_2}, questa dovrà avere equazione della forma {x=x_{M_2}}. Di conseguenza possiamo scrivere:

r_2:x=1

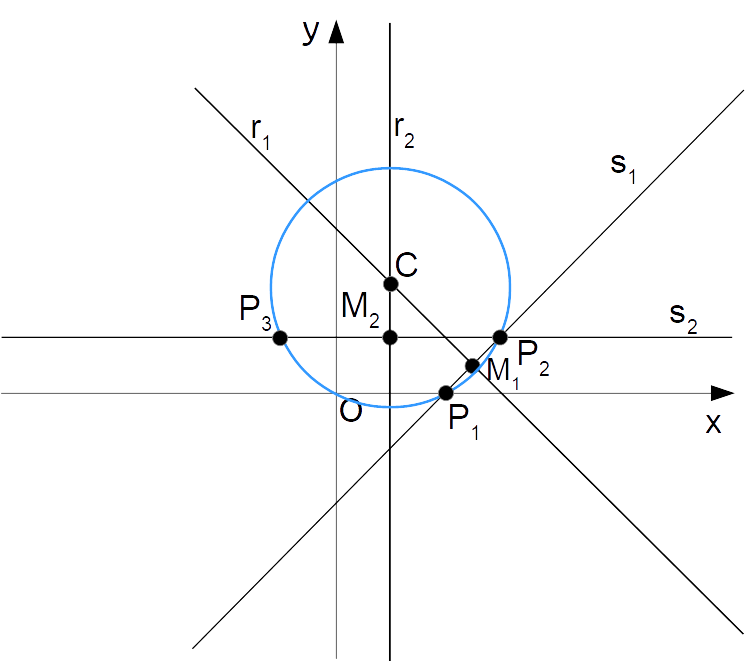
Ora, per ricavare le coordinate del centro della circonferenza basta scrivere il sistema che contiene le equazioni delle rette {r_1} ed {r_2}, in modo da ricercare i valori delle coordinate del punto di intersezione tra le due rette stesse (che coincide con il centro della circonferenza):

\begin{cases} y=-x+3 \\ \\ x=1\end{cases}

La risoluzione del sistema è piuttosto immediata e fornisce:

\begin{cases} y=2 \\ \\ x=1\end{cases}

Di conseguenza il centro della circonferenza passante per i punti {P_1}, {P_2} e {P_3} è {C=(1,2)}.

Infine, possiamo calcolare il raggio della circonferenza come distanza ad esempio tra il centro {C} e il punto {P_1=(2,0)}:

\begin{align*} & d(C, P_1)=\overline{CP_1}=\sqrt{(x_{P_1}-x_C)^2+(y_{P_1}-y_C)^2}=\\ \\ & =\sqrt{(2-1)^2+(0-2)^2} =\sqrt{1+4}=\sqrt{5}\end{align*}

E’ a questo punto immediato scrivere l’equazione della circonferenza con centro e raggio:

(x-1)^2+(y-2)^2=5

Infine, l’equazione riespressa in forma canonica diviene:

\begin{align*} &x^2-2x+1+y^2-4y+4=5; \\ \\ & \boxed{x^2+y^2-2x-4y=0}\end{align*}

Abbiamo così determinato l’equazione (anche in forma canonica) della circonferenza del piano cartesiano passante per i tre punti assegnati.

Riassumiamo brevemente i passi da seguire per scrivere l’equazione della circonferenza passante per i punti del piano {P_1, \: P_2, \: P_3} non allineati tra loro, utilizzando il metodo della ricerca del centro e del raggio:

• scrivere le equazioni delle rette {s_1} ed {s_2} passanti rispettivamente per i punti {P_1, P_2} e per i punti {P_2, P_3};
• determinare le coordinate dei punti medi dei segmenti {\overline{P_1P_2}} e {\overline{P_2P_3}};
• scrivere le equazioni delle rette {r_1} ed {r_2} passanti per i punti medi ottenuti e perpendicolari rispettivamente alle rette {s_1} ed {s_2}. Tali rette sono gli assi dei segmenti {\overline{P_1P_2}} e {\overline{P_2P_3}};
• determinare il punto di intersezione tra le rette {r_1} ed {r_2}, ottenendo il centro della circonferenza {C};
• calcolare il raggio della circonferenza come distanza ad esempio tra il centro {C} e il punto {P_1};
• infine, utilizzando le coordinate del centro e la misura del raggio, scrivere l’equazione della circonferenza corrispondente, ottenendo così l’equazione della circonferenza passante per i tre punti dati.

Equazione della circonferenza a partire dalle coordinate di tre punti non allineati con le condizioni di appartenenza

Vediamo ora un altro metodo per scrivere l’equazione della circonferenza che passa per tre punti non allineati.

Ricordiamo che se un punto {P=(x_P, y_P)} appartiene ad una circonferenza {\gamma: x^2+y^2+ax+by+c=0}, le coordinate di tale punto dovranno soddisfare l’equazione della circonferenza stessa. In altre parole, sostituendo i valori di {x_P} ed {y_P} rispettivamente alle lettere {x} e {y} nell’equazione della circonferenza, si dovrà ottenere l’uguaglianza {0=0}. Se ciò si verifica diremo che il punto {P} soddisfa la condizione di appartenenza alla circonferenza {\gamma}.

Ora, dati tre punti non allineati {P_1=(x_1, y_1), \: P_2=(x_2, y_2), \: P_3 = (x_3, y_3)}, questi dovranno necessariamente appartenere ad una certa circonferenza {\gamma}. Di conseguenza, ciascun punto dovrà soddisfare la condizione di appartenenza alla circonferenza stessa. Così dovranno valere contemporaneamente le seguenti uguaglianze:

\begin{align*} &x_1^2+y_1^2+ax_1+by_1+c=0 \qquad \text{appartenenza di } P_1 ; \\ \\ & x_2^2+y_2^2+ax_2+by_2+c=0 \qquad \text{appartenzenza di }P_2; \\ \\ &x_3^2+y_3^2+ax_3+by_3+c=0 \qquad \text{appartenenza di }P_3  \end{align*}

Ma richiedere che tali uguaglianze risultino verificate contemporaneamente equivale a richiedere che per certi valori di {a,b,c } dovrà risultare determinato il seguente sistema:

\begin{cases}x_1^2+y_1^2+ax_1+by_1+c=0 \\ \\ x_2^2+y_2^2+ax_2+by_2+c=0 \\ \\  x_3^2+y_3^2+ax_3+by_3+c=0\end{cases}

Così, a partire dalle coordinate dei punti {P_1, \: P_2, \: P_3} non allineati tra loro, l’idea è quella di scrivere un tale sistema, ricercando i valori delle incognite {a, \: b, \: c}. E poiché tali incognite rappresentano i coefficienti dell’equazione di una circonferenza in forma canonica, una volta ottenute le soluzioni del sistema sarà possibile scrivere l’equazione della circonferenza passante per i tre punti dati.

Esempio 2 (circonferenza per tre punti con le condizioni di appartenenza)

Determinare l’equazione della circonferenza passante per i punti non allineati fra loro {P_1=(2,-3), \: P_2=(4,-1), \: P_3=(0,1)}.

Sostituendo le coordinate rispettivamente dei punti {P_1, \: P_2} e {P_3} nell’equazione di una generica circonferenza in forma canonica {x^2+y^2+ax+by+c=0}, otteniamo tre equazioni nelle incognite {a, b, c} che rappresentano la condizione di appartenenza di ciascun punto alla circonferenza. Abbiamo:

\begin{cases}2^2+(-3)^2+2a-3b+c=0 \\ \\ 4^2+(-1)^2+4a-b+c=0 \\ \\ 0^2+1^2+0a+b+c=0\end{cases}

ovvero:

\begin{cases} 4+9+2a-3b+c=0 \\ \\ 16+1+4a-b+c=0 \\ \\ 1+b+c=0\end{cases}

Sommando i termini simili e riordinando i termini:

\begin{cases} 2a-3b+c=-13 \\ \\ 4a-b+c=-17\\ \\ b+c=-1\end{cases}

Osserviamo che abbiamo portato i termini noti al secondo membro in modo da ricondurre il sistema alla forma normale.

Il sistema è di tre equazioni nelle tre incognite {a, \: b, \: c}. Per risolverlo possiamo utilizzare ad esempio il metodo di Cramer.

Per non incorre in errori, riscriviamo la terza equazione riportando esplicitamente anche il termine in {a}, anche se ha coefficiente nullo. Abbiamo:

\begin{cases} 2a-3b+c=-13 \\ \\ 4a-b+c=-17\\ \\ 0a+ b+c=-1\end{cases}

Calcoliamo il determinante della matrice dei coefficienti, ad esempio utilizzando la regola di Sarrus:

\begin{align*} & D=\det \begin{pmatrix} 2  & -3 & 1 \\ 4 & -1 & 1 \\ 0 & 1 & 1\end{pmatrix}=\\ \\ & =2 \cdot (-1) \cdot 1 + (-3) \cdot 1 \cdot 0 + 1 \cdot 4 \cdot 1- 0 \cdot (-1)\cdot1-1 \cdot 1 \cdot 2-1 \cdot 4 \cdot -3=\\ \\ & =-2+0+4-0-2+12=12 \end{align*}

Proseguiamo calcolando i determinanti {D_x, \: D_y, \: D_z}, che nel nostro caso scriviamo come {D_a, \: D_b, \: D_c} dato che le incognite sono i coefficienti {a,\: b, \:c}:

\small\begin{align*} &D_a=\det \begin{pmatrix} -13 & -3 & 1\\ -17 &-1 & 1\\ -1 &1 & 1\end{pmatrix}=\\ \\ & =(-13) \cdot (-1) \cdot 1+(-3) \cdot 1 \cdot (-1) + 1 \cdot (-17) \cdot 1-(-1)\cdot(-1) \cdot 1 - 1 \cdot 1 \cdot (-13)+ \\ \\ & -1 \cdot (-17) \cdot (-3)=\\ \\ & =13+3-17-1+13-51=-40\end{align*}

\begin{align*} &D_b = \det \begin{pmatrix} 2 & -13 &  1\\ 4 & -17  & 1\\0  & -1 & 1  \end{pmatrix}=\\ \\ & =2 \cdot (-17)\cdot1+(-13)\cdot1\cdot0+1 \cdot 4 \cdot (-1)-0 \cdot (-17)\cdot1-(-1)\cdot1\cdot2-1 \cdot 4 \cdot (-13)=\\ \\ & =-34+0-4-0+2+52=16\end{align*}

\begin{align*} &D_c=\det \begin{pmatrix}2 & -3 & -13\\ 4 & -1  &-17\\ 0 & 1 &-1 \end{pmatrix}=\\ \\ & =2 \cdot (-1) \cdot (-1)+(-3) \cdot (-17) \cdot 0 +(-13)\cdot4 \cdot 1-0 \cdot (-1) \cdot (-13)-1 \cdot (-17) \cdot 2 +\\ \\ & -(-1) \cdot 4 \cdot (-3) =\\ \\ & =2+0-28-52-0+34-12=-28\end{align*}

Otteniamo per il sistema le soluzioni:

\small a=\dfrac{D_a}{D}=\dfrac{-40}{12}=-\dfrac{10}{3}; \qquad b=\dfrac{D_b}{D}=\dfrac{16}{12}=\dfrac{4}{3}; \qquad c=\dfrac{D_c}{D}=\dfrac{-28}{12}=-\dfrac{7}{3}

Siamo a questo punto in grado di scrivere l’equazione della circonferenza direttamente in forma canonica, poiché disponiamo dei coefficienti {a,b,c} necessari:

x^2+y^2-\dfrac{10}{3}x+\dfrac{4}{3}y-\dfrac{7}{3}=0

E questa è in conclusione l’equazione della circonferenza passante per i tre punti dati.

Per scrivere l’equazione della circonferenza passante per tre punti non allineati, quale fra i due metodi utilizzare? Sicuramente entrambi presentano vantaggi e svantaggi. In particolare, il metodo basato sulla ricerca del centro e del raggio richiede molti ragionamenti a livello di geometria analitica, ma dal punto di vista algebrico richiede di risolvere un sistema molto semplice. Viceversa, il metodo basato sulle condizioni di appartenenza dei punti alla circonferenza non richiede un particolare sforzo di ragionamento ma porta comunque a dover risolvere un sistema di tre equazioni in tre incognite. Per cui come al solito, consigliamo di orientarvi verso il metodo che più vi resta comodo, tenendo comunque conto delle indicazioni del vostro insegnante.

Centro e coordinate di un punto come condizioni per determinare l’equazione di una circonferenza

Proseguiamo lo studio delle condizioni per determinare l’equazione di una circonferenza esaminando un altro caso. Supponiamo di conoscere le coordinate del centro {C} di una circonferenza e le coordinate di un punto {P} ad essa appartenente. Tali dati sono sufficienti per scrivere l’equazione della circonferenza? E sono tutti necessari?

La risposta è sì. Infatti, dalle coordinate del centro e dalle coordinate di un punto della circonferenza è immediato ricavare la misura del raggio. Si tratta infatti, per definizione, della distanza tra i punti {C} e {P}:

r=\overline{CP}=\sqrt{(x_P-x_C)^2+(y_P-y_C)^2}

Ma una volta noti raggio e centro, come sappiamo è possibile scrivere immediatamente l’equazione della circonferenza nella forma con centro e raggio:

(x-x_C)^2+(y-y_C)^2=r^2

Inoltre sviluppando i quadrati, sommando i termini simili e portando tutto al primo membro è possibile ricondurre l’equazione alla forma canonica. In alternativa, è possibile ricavare i coefficienti {a, \: b,\: c} con le opportune formule.

Esempio 3 (circonferenza con coordinate del centro e di un suo punto)

Scrivere l’equazione di una circonferenza avente centro {C=(3,0)} ed alla quale appartiene il punto {P=(6,4)}.

A partire dalle coordinate dei punti {C} e {P}, ricaviamo la misura del raggio:

\begin{align*} &r = \sqrt{(x_P-x_C)^2+(y_P-y_C)^2}=\sqrt{(6-3)^2+(4-0)^2}=\\ \\ & =\sqrt{9+16}=\sqrt{25}=5\end{align*}

Così l’equazione nella forma con centro e raggio della circonferenza cercata è:

(x-3)^2+(y-0)^2=5^2

ovvero:

(x-3)^2+y^2=25

Sviluppando il quadrato al primo membro:

x^2-6x+9+y^2=25

Portando infine tutto al primo membro sommando i termini simili:

x^2+y^2-6x-16=0

e questa è in conclusione l’equazione in forma canonica della circonferenza cercata.

Equazione della circonferenza a partire dalle coordinate di due suoi punti e dall’equazione di una retta passante per il suo centro

Un altro insieme di condizioni per determinare l’equazione di una circonferenza è dato dalla conoscenza delle coordinate di due punti della circonferenza e dell’equazione di una retta che passa per il centro della circonferenza stessa.

Osserviamo, come si può intuire dalla figura, che conoscendo le coordinate dei punti {P_1, \: P_2} e l’equazione della retta passante per il centro della circonferenza {r_C}, è possibile risalire alle coordinate del centro della circonferenza. Ed a tal punto, una volta calcolato il raggio, riusciamo a scrivere l’equazione della circonferenza cercata.

In particolare, le coordinate del centro si individuano tramite l’intersezione fra la retta {r_C}, la cui equazione è nota, e la retta {r_{12}}, asse del segmento {\overline{P_1P_2}}. E come abbiamo visto all’inizio della lezione, l’equazione dell’asse di un segmento si ottiene a partire dall’equazione della retta passante per i due estremi del segmento, imponendo la condizione di perpendicolarità della retta {r_{12}} rispetto alla retta passante per {P_1, \: P_2} e imponendo inoltre il passaggio della retta {r_{1,2}} nel punto medio del segmento {\overline{P_1P_2}}.

Prestando attenzione al seguente esempio quanto detto risulterà più chiaro.

Esempio 4

Scrivere l’equazione della circonferenza passante per i punti {P_1=(1,4)} e {P_2=(-2, 1)} e il cui centro {C} appartiene alla retta {r_C} di equazione {3x-y+4=0}.

Cominciamo calcolando il coefficiente angolare della retta che passa per i punti {P_1} e {P_2}. Ci interessa poiché è il coefficiente angolare della retta parallela al segmento {\overline{P_1P_2}}, del quale poi dovremo determinare l’equazione dell’asse. Abbiamo:

m=\dfrac{y_{P_2}-y_{P_1}}{x_{P_2}-x_{P_1}}

Sostituendo i valori delle coordinate dei due punti:

m=\dfrac{1-4}{-2-1}=\dfrac{-3}{-3}=1

Ora determiniamo {M_{12}}, ovvero il punto medio del segmento {\overline{P_1P_2}}:

\begin{align*} & M_{12}=\left( \dfrac{x_{P_1}+x_{P_2}}{2}, \dfrac{y_{P_1}+y_{P_2}}{2}\right)=\\ \\ & =\left( \dfrac{1-2}{2}, \dfrac{4+1}{2}\right)=\left( -\dfrac{1}{2}, \dfrac{5}{2}\right) \end{align*}

Scriviamo a questo punto l’equazione della retta {r_{12}} perpendicolare alla retta passante per {P_1} e {P_2} ed inoltre tale da passare per il punto {M_1}. La retta {r_{12}} in altre parole è l’asse del segmento {\overline{P_1P_2}}:

y-y_{M_{12}}=-\dfrac{1}{m}(x-x_{M_{12}}) \quad \Rightarrow \quad y-\dfrac{5}{2}=-1 \left(x+\dfrac{1}{2}\right)

Svolendo i calcoli otteniamo in conclusione per la retta {r_{1,2}}:

r_{1,2}:y=-x+2

Ma ormai siamo quasi arrivati, poiché le coordinate del centro della circonferenza si ottengono dall’intersezione della retta {r_{1,2}} con la retta {r_C}, la cui equazione è nota dal testo:

\begin{cases} r_{1,2}: y=-x+2 \\ \\ r_C:  3x-y+4=0\end{cases}

Per risolvere il sistema, riscriviamo l’equazione della retta {r_C} in forma esplicita, e quindi utilizziamo il metodo del confronto:

\small \begin{align*} &\begin{cases} y=-x+2  \\ \\ y=3x+4\end{cases}\end{align*} \quad  \Rightarrow \quad \begin{cases} -x+2=3x+4 \\ \\ y=3x+4  \end{cases} \quad \Rightarrow \quad \begin{cases} 4x=2-4 \quad \rightarrow \:x=-\dfrac{1}{2} \\ \\ y=3x+4 \quad \rightarrow \:y=\dfrac{5}{2}\end{cases}

Così il centro della circonferenza è dato dal punto {C=\left( -\dfrac{1}{2}, \dfrac{5}{2}\right)}. Infine, per il raggio basta calcolare la distanza ad esempio tra il punto {C} e il punto {P_1}:

\small \begin{align*} & r=\overline{CP_1}=\sqrt{(x_{P_1}-x_C)^2+(y_{P_1}-y_C)^2}=\sqrt{\left(1+\dfrac{1}{2}\right)^2+\left( 4-\dfrac{5}{2}\right)^2}=\\ \\ & =\sqrt{\dfrac{9}{2}}=\dfrac{\sqrt{9}}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{\sqrt{18}}{2}\end{align*}

Disponendo di centro e raggio possiamo concludere scrivendo l’equazione della circonferenza cercata:

\begin{align*} &\left( x+\dfrac{1}{2}\right)^2+\left( y-\dfrac{5}{2}\right)^2=\left( \dfrac{\sqrt{18}}{2}\right)^2; \\ \\ & x^2+\dfrac{1}{4}+x+y^2+\dfrac{25}{4}-5y-\dfrac{18}{4}=0;\\ \\ & \boxed{x^2+y^2+x-5y+2=0}\end{align*}

Rimane ora da studiare un ultimo caso, ovvero quello relativo ad una circonferenza della quale siano note le coordinate del centro e l’equazione di una retta ad essa tangente.

Condizioni per determinare l’equazione di una circonferenza: coordinate del centro ed equazione della retta tangente alla circonferenza stessa

Consideriamo il caso relativo ad una circonferenza della quale conosciamo:

• le coordinate del centro, {C=(x_C, y_C)};
• l’equazione di una retta tangente alla circonferenza, ad esempio nella forma implicita {a_1x+b_1y+c_1=0}.

Per quanto visto sulla lezione per la determinazione dell’equazione della retta tangente ad una circonferenza in un suo punto, la distanza tra la retta tangente e il centro della circonferenza equivale alla misura del raggio. Di conseguenza, basterà calcolare il raggio utilizzando la formula per la distanza tra una retta e un punto nel piano. E, in conclusione, potremo scrivere l’equazione della circonferenza, in quanto centro e raggio sono noti.

Esempio 5

Determinare l’equazione della circonferenza di centro {C=(-3,-5)} e tangente alla retta {t} di equazione {2x+9y-7=0}.

Calcoliamo la distanza fra la retta {t} e il punto {C}. Ricordiamo la formula da utilizzare, nel caso di equazione della retta data in forma implicita:

d(P,r)=\dfrac{|ax_P+by_P+c|}{\sqrt{a^2+b^2}}

Nel caso in esame:

\begin{align*} &d(C, t)=\dfrac{|2 \cdot (-3)+9 \cdot (-5)-7|}{\sqrt{2^2+9^2}}=\\ \\ & =\dfrac{|-6-45-7|}{\sqrt{85}}=\dfrac{58}{\sqrt{85}}=r\end{align*}

Per definizione, la distanza ottenuta corrisponde alla misura del raggio della circonferenza cercata. Ma essendo anche note le coordinate del centro, possiamo concludere l’esercizio scrivendo l’equazione della circonferenza:

\begin{align*} &(x+3)^2+(y+5)^2=\left( \dfrac{58}{\sqrt{85}}\right)^2; \\ \\ & x^2+6x+9+y^2+10y+25=\dfrac{3364}{85};\\ \\ & \boxed{x^2+y^2+6x+10y-\dfrac{474}{85}}=0\end{align*}

Conclusioni

Abbiamo quindi visto le condizioni necessarie e sufficienti per determinare l’equazione di una circonferenza nel piano, nei vari casi. Tutti i ragionamenti fatti si basano sulla geometria euclidea e su quanto sappiamo sulla geometria analitica, non solo a proposito della circonferenza ma anche della retta nel piano. E le nozioni relative all’equazione della retta, il coefficiente angolare, la retta passante per un punto con pendenza nota e la relazione di perpendicolarità fra rette sono tutte fondamentali per poter muoversi con una certa sicurezza nello studio delle condizioni per determinare l’equazione di una circonferenza nel piano.

Un saluto a tutti voi e buon proseguimento con SìMatematica!