Fascio di circonferenze

 - 

Circonferenza (scuole superiori)

Un fascio di circonferenze è un insieme di infinite circonferenze che possono essere tra loro secanti, tangenti, concentriche oppure esterne. Il fascio è rappresentabile mediante un’equazione parametrica che corrisponde ad una determinata circonferenza per certi valori del parametro reale.

Dopo aver visto come rappresentare una circonferenza mediante un’equazione (nelle due forme con centro e raggio e canonica), in questa lezione ci occupiamo del fascio di circonferenze.

Come nel caso della retta abbiamo incontrato i fasci di rette, così anche nel caso della circonferenza è possibile stabilire la nozione di fascio. Un fascio di circonferenze, in particolare, può essere costruito a partire da due circonferenze aventi determinate proprietà. Infatti, come vedremo fra un istante il tipo di fascio di circonferenze cambia in base al fatto che le due circonferenze di partenza siano secanti o tangenti, oppure che queste abbiano i centri in comune oppure no.

E allo stesso modo dei fasci di rette, costruiremo un fascio di circonferenze come combinazione lineare delle equazioni delle due circonferenze di partenza. E anche in questo caso faremo uso, sotto opportune ipotesi, di un solo parametro reale.

Equazione di un fascio di circonferenze

Consideriamo due distinte circonferenze {\mathscr{C}_1} e {\mathscr{C}_2}, reali non degeneri, aventi equazioni espresse in forma canonica:

\small \mathscr{C}_1: x^2+y^2+a_1x+b_1y+c_1=0, \qquad \mathscr{C}_2: x^2+y^2+a_2x+b_2y+c_2=0

Ora, sommiamo membro a membro le due equazioni tra loro, avendo allo stesso tempo cura di moltiplicare i primi membri delle equazioni rispettivamente per degli opportuni parametri reali {\lambda} e {\mu}:

\small \lambda(x^2+y^2+a_1x+b_1y+c_1)+\mu(x^2+y^2+a_2x+b_2y+c_2)=0

Tale equazione rappresenta per definizione una combinazione lineare delle due equazioni di partenza. Ed in particolare, per {\lambda = 0} e {\mu \neq 0} ritroviamo l’equazione della circonferenza {\mathscr{C}_2}, mentre per {\lambda \neq 0} e {\mu = 0} ritroviamo l’equazione della circonferenza {\mathscr{C}_1}.

Eseguiamo i prodotti al primo membro, ottenendo:

\lambda x^2+\lambda y^2+ \lambda a_1x + \lambda b_1y +\lambda c_1+\mu x^2 + \mu y^2 + \mu a_2x+\mu b_2y+\mu c_2=0

Scriviamo di seguito i termini in {x^2}, poi quelli in {y^2}, poi quelli in {x}, quelli in {y} ed infine i termini noti:

\lambda x^2+\mu x^2+\lambda y^2+\mu y^2+\lambda a_1x +\mu a_2x+\lambda b_1 y+\mu b_2y+\lambda c_1+\mu c_2=0

Ora raccogliamo parzialmente per {x^2, y^2, x, y}:

\small (\lambda + \mu)x^2+(\lambda + \mu)y^2+(\lambda a_1 + \mu a_2)x+(\lambda b_1 + \mu b_2)y+\lambda c_1+\mu c_2 = 0 \qquad (*)

Ponendo {A(\lambda, \mu)=\lambda + \mu}, {B(\lambda, \mu)=\lambda a_1 + \mu a_2}, {C(\lambda, \mu)=\lambda b_1 + \mu b_2} e infine {D(\lambda, \mu)=\lambda c_1 + \mu c_2} ritroviamo un’equazione della forma dell’equazione di una circonferenza, anche se non canonica:

\small A(\lambda, \mu)x^2+A(\lambda, \mu)y^2+B(\lambda, \mu)x+C(\lambda, \mu)y+D(\lambda, \mu)=0 

Di conseguenza, fissati opportuni valori di {\lambda} e {\mu}, all’equazione appena scritta corrisponderà l’equazione di una circonferenza. E per ogni opportuna scelta dei valori dei parametri {\lambda} e {\mu} otterremo l’equazione di una circonferenza differente.

Osserviamo che affinché l’equazione effettivamente sia della forma di quella di una circonferenza dovrà essere chiaramente {A \neq 0} ( e quindi {\lambda + \mu \neq 0}). Diversamente, i termini di secondo grado sparirebbero.

Prestiamo attenzione al fatto che i coefficienti {A(\lambda, \mu),B(\lambda, \mu),C(\lambda, \mu),D(\lambda, \mu)} scritti sono funzioni dei parametri reali {\lambda} e {\mu}. Così al variare di tali parametri si otterrà un fascio di circonferenze avente per generatrici le circonferenze {\mathscr{C}_1} e {\mathscr{C}_2}. In altre parole, lo sottolineiamo ancora, ad ogni scelta di valori da attribuire opportunamente ai parametri {\lambda} e {\mu} si otterranno determinati valori dei coefficienti nell’equazione, e di conseguenza avremo la particolare circonferenza corrispondente ad essi.

Nota: per i parametri sono accettabili quei valori che corrispondono a circonferenze reali non degeneri.

Ora, riprendiamo l’equazione del fascio nella forma *. Ipotizziamo che sia {\lambda \neq 0}. In tal caso, dividendo ciascun termine per {\lambda} in base al secondo principio di equivalenza abbiamo:

\scriptsize\left( \dfrac{\lambda + \mu}{\lambda}\right)x^2+ \left( \dfrac{\lambda + \mu}{\lambda}\right)y^2+\left( \dfrac{\lambda a_1 + \mu a_2}{\lambda}\right)x+\left( \dfrac{\lambda b_1 + \mu b_2}{\lambda}\right)y+\dfrac{\lambda}{\lambda} c_1+\dfrac{\mu}{\lambda} c_2 = 0

ovvero:

\left( 1+\dfrac{\mu}{\lambda}\right)x^2+\left(1+ \dfrac{\mu}{\lambda}\right)y^2+\left( a_1+\dfrac{\mu}{\lambda}a_2\right)x+\left(b_1+ \dfrac{\mu}{\lambda}b_2\right)y+c_1+\dfrac{\mu}{\lambda}c_2=0

Ponendo infine {\dfrac{\mu}{\lambda}=k}:

\small (1+k)x^2+(1+k)y^2+(a_1+ka_2)x+(b_1+kb_2)y+c_1+kc_2=0 \qquad (**)

Osserviamo che deve valere la condizione {1+k \neq 0 }, altrimenti i termini di secondo grado sparirebbero. Ciò equivale a richiedere {k \neq -1}.

In conclusione l’equazione ** rappresenta il fascio di circonferenze avente per generatrici le circonferenze {\mathscr{C}_1} e {\mathscr{C}_2}. E in questo caso compare più comodamente il solo parametro reale {k}.

Tuttavia, per poter utilizzare un solo parametro abbiamo dovuto porre la condizione {\lambda \neq 0}. Ciò significa che la circonferenza {\mathscr{C}_2}, la cui equazione in precedenza si otteneva per {\lambda = 0}, resta esclusa dal fascio.

Forniamo a questo punto la definizione generale di fascio di circonferenze.

Definizione. Date due circonferenze reali non degeneri:{\mathscr{C}_1: x^2+y^2+a_1x+b_1y+c_1=0, \qquad \mathscr{C}_2: x^2+y^2+a_2x+b_2y+c_2=0}il fascio di circonferenze da esse generato ha equazione:{\small (1+k)x^2+(1+k)y^2+(a_1+ka_2)x+(b_1+kb_2)y+c_1+kc_2=0 \qquad (**) } con {k \neq -1}.

Ora, come vedremo tra un istante il tipo di fascio considerato dipende da come si presentano le circonferenze che lo generano. In particolare abbiamo i seguenti casi:

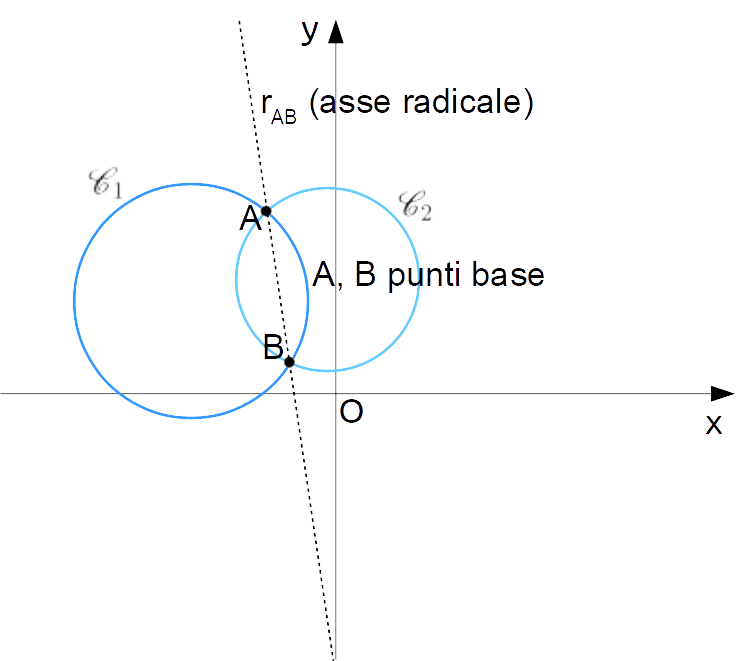
• le circonferenze generatrici del fascio sono secanti, ovvero hanno due punti {A} e {B} in comune tra loro. In questo caso come vedremo tutte le circonferenze del fascio passano per i punti {A} e {B} (detti punti base). Inoltre, la retta passante per i punti {A} e {B} si dice asse radicale del fascio;
• le circonferenze generatrici sono tangenti in un certo punto {A}. In altre parole, le circonferenze generatrici hanno nel punto {A} la stessa retta tangente. In questo caso le circonferenze del fascio passano tutte per il punto {A} (detto punto base) ed in tale punto risultano tangenti sempre alla stessa retta;
• ancora, le circonferenze generatrici sono tra loro concentriche. In tal caso come vedremo le due circonferenze condividono gli stessi coefficienti {a} e {b} (da essi infatti come sappiamo dipendono le coordinate del centro);
• infine, le due circonferenze generatrici non hanno punti in comune e non sono concentriche.

Analizziamo nel seguito i primi tre casi nel dettaglio, che sono quelli di nostro interesse.

Fascio di circonferenze secanti

Consideriamo due circonferenze del piano cartesiano {\mathscr{C}_1} e {\mathscr{C_2}}, tali da essere secanti, ovvero tali da avere due punti {A} e {B} in comune tra loro:

Le due circonferenze hanno equazioni:

\mathscr{C}_1: x^2+y^2+a_1x+b_1y+c_1=0, \qquad \mathscr{C}_2: x^2+y^2+a_2x+b_2y+c_2=0

Osserviamo che i punti {A} e {B} appartengono ad entrambe le circonferenze. Quindi, le coordinate di tali punti soddisfano le condizioni di appartenenza a ciascuna circonferenza. Di conseguenza, se costruiamo un fascio a partire dalle equazioni delle circonferenze {\mathscr{C}_1} e {\mathscr{C}_2}, l’equazione del fascio corrispondente sarà necessariamente tale da essere soddisfatta per i valori delle coordinate dei punti {A} e {B}. Ricordiamo infatti che l’equazione del fascio si ottiene come combinazione lineare delle equazioni delle due circonferenze.

Così, tutte le circonferenze del fascio passeranno per i punti {A} e {B}. Per questa particolarità, i due punti vengono indicati con il nome di punti base del fascio.

La retta passante per i punti {A} e {B} viene invece detta asse radicale del fascio.

Riprendiamo a questo punto, per comodità, l’equazione del fascio di circonferenze:

\small (1+k)x^2+(1+k)y^2+(a_1+ka_2)x+(b_1+kb_2)y+c_1+kc_2=0 \qquad (**)

che nel nostro caso avrà i coefficienti {a_1, b_1, c_1} e {a_2, b_2, c_2} relativi alle circonferenze {\mathscr{C}_1} e {\mathscr{C}_2} tra loro secanti.

Se imponiamo {k=-1} i termini di secondo grado spariscono e ci riconduciamo alla seguente equazione di una retta:

(a_1-a_2)x+(b_1-b_2)y+c_1-c_2=0

Ora, si può dimostrare che tale retta è proprio la retta passante per i due punti {A} e {B}, ovvero l’asse radicale del fascio.

Per dimostrarlo, studiamo le intersezioni tra le due circonferenze {\mathscr{C}_1} e {\mathscr{C}_2}. Allo scopo, mettiamo a sistema le equazioni delle circonferenze {\mathscr{C}_1} e {\mathscr{C_2}}:

\begin{cases} x^2+y^2+a_1x+b_1y+c_1=0 \\ \\ x^2+y^2+a_2x+b_2y+c_2=0\end{cases}

Applicando il metodo di riduzione, sottraiamo alla prima equazione la seconda. Consideriamo singolarmente la nuova equazione che così si ottiene:

\begin{align*} &\cancel{x^2}+\cancel{y^2}+a_1x+b_1y+c_1-\cancel{x^2}-\cancel{y^2}-a_2x-b_2y-c_2=0;\\ \\ &a_1x-a_2x+b_1y-b_2y+c_1-c_2=0;
\\ \\ & \boxed{(\underbrace{a_1-a_2}_{a})x+(\underbrace{b_1-b_2}_{b})y+\underbrace{c_1-c_2}_{c}=0} \end{align*}

Ora, dato che otteniamo tale equazione imponendo che le due circonferenze si intersechino, è evidente che l’equazione sarà soddisfatta dalle coordinate di entrambi i punti di intersezione delle circonferenze. E trattandosi dell’equazione di una retta, poiché della forma {ax+by+c=0}, è altrettanto chiaro che si tratta dell’equazione corrispondente proprio alla retta passante per i punti di intersezione tra le circonferenze.

Ritroviamo in questo modo l’equazione dell’asse radicale del fascio, che effettivamente è la retta passante per i due punti {A} e {B} di intersezione tra le due circonferenze secanti. Quindi abbiamo dimostrato che per {k=-1} dall’equazione del fascio di circonferenze otteniamo l’equazione dell’asse radicale.

Asse centrale di un fascio di circonferenze secanti

I centri di tutte le circonferenze che appartengono ad un fascio di circonferenze secanti giacciono su una retta che è detta asse centrale. Tale retta è perpendicolare all’asse radicale del fascio.

L’asse centrale può essere di conseguenza visto come la retta che unisce i centri delle circonferenze generatrici del fascio, oppure come la retta perpendicolare all’asse radicale e tale da passare per il centro di una circonferenza generatrice del fascio. Con queste due osservazioni sarà possibile ricavare negli esercizi l’equazione dell’asse centrale di una fascio.

La dimostrazione del fatto che l’asse centrale è perpendicolare all’asse radicale è disponibile, in via del tutto facoltativa, alla fine della lezione.

Forme alternative per l’equazione di un fascio di circonferenze secanti

Riprendiamo l’equazione di una fascio di circonferenze con generatrici secanti nella seguente forma:

\small \lambda(x^2+y^2+a_1x+b_1y+c_1)+\mu(x^2+y^2+a_2x+b_2y+c_2)=0

Ponendo {\lambda \neq 0} e dividendo i termini per {\lambda} come segue:

\small \dfrac{\lambda}{\lambda}(x^2+y^2+a_1x+b_1y+c_1)+\dfrac{\mu}{\lambda}(x^2+y^2+a_2x+b_2y+c_2)=0

otteniamo l’equazione:

\small x^2+y^2+a_1x+b_1y+c_1+\dfrac{\mu}{\lambda}(x^2+y^2+a_2x+b_2y+c_2)=0

ed infine ponendo {\dfrac{\mu}{\lambda}=k}:

\small x^2+y^2+a_1x+b_1y+c_1+k(x^2+y^2+a_2x+b_2y+c_2)=0 \qquad (****)

L’equazione ottenuta è molto simile a quella a suo tempo vista per i fasci di rette. Nell’equazione è possibile individuare i primi membri delle equazioni delle circonferenze generatrici {\mathscr{C}_1} e {\mathscr{C}_2}.

Vogliamo ora mostrare la possibilità di esprimere l’equazione di un fascio di circonferenze con generatrici secanti anche come combinazione lineare dell’equazione di una delle due circonferenze generatrici e dell’equazione dell’asse radicale.

Riprendiamo l’equazione del fascio di circonferenze **:

\small (1+k)x^2+(1+k)y^2+(a_1+ka_2)x+(b_1+kb_2)y+c_1+kc_2=0 \qquad (**)

Vogliamo mostrare che anche la seguente equazione esprime lo stesso fascio di circonferenze con generatrici secanti:

\small x^2+y^2+a_1x+b_1y+c_1+h[(a_1-a_2)x+(b_1-b_2)y+c_1-c_2]=0 \qquad (***)

con {h} parametro reale diverso da {k}.

Si tratta in particolare della combinazione lineare delle equazioni della circonferenza {\mathscr{C}_1} e della retta passante per {A} e {B} (asse radicale del fascio).

Sviluppiamo i prodotti dell’ultima equazione scritta:

\begin{align*} &x^2+y^2+a_1x+b_1y+c_1+ha_1x-ha_2x+hb_1y-hb_2y+hc_1-hc_2 = 0\end{align*}

Raccogliendo parzialmente per {x} e {y} abbiamo:

x^2+y^2+(a_1+ha_1-ha_2)x+(b_1+hb_1-hb_2)y+c_1+hc_1-hc_2=0

Come possiamo vedere l’equazione ha la forma dell’equazione canonica di una circonferenza, ma con coefficienti dipendenti dal parametro reale {h}. Di conseguenza, per ogni valore di {h} otterremo una determinata equazione in forma canonica. E inoltre, poiché l’equazione risulta dalla combinazione lineare dell’equazione di {\mathscr{C}_1} e dell’equazione dell’asse radicale, tutte le circonferenze (reali non degeneri) che si ottengono al variare di {h} passano necessariamente per i punti base, ovvero i punti {A} e {B}. Ma allora anche l’equazione *** rappresenta il fascio con generatrici le circonferenze {\mathscr{C}_1} e {\mathscr{C}_2}.

Vediamo ora degli esempi sui fasci di circonferenze secanti.

Esempio 1 (fasci di circonferenze secanti)

Scrivere l’equazione del fascio generato dalle circonferenze {\mathscr{C}_1: x^2+y^2-1=0} e {\mathscr{C}_2: x^2+y^2-2x=0}. Determinare inoltre i punti base ed esprimere l’equazione del fascio anche utilizzando l’equazione dell’asse radicale.

Cominciamo determinando i punti base del fascio. Questi sono i punti {A} e {B} che risultano dall’intersezione delle due circonferenze generatrici. Mettendo allora a sistema le equazioni di tali circonferenze abbiamo:

\begin{cases}\mathscr{C}_1: x^2+y^2-1=0 \\ \\  \mathscr{C}_2: x^2+y^2-2x=0\end{cases}

Siamo di fronte ad un sistema non lineare avente due equazioni di secondo grado rispetto alle variabili {x} e {y}. Applichiamo il metodo di riduzione sottraendo la seconda equazione alla prima, e sostituendo la nuova equazione che così si ottiene alla prima equazione a sistema:

\begin{cases}\cancel{ x^2}+\cancel{y^2}-1-\cancel{x^2}-\cancel{y^2}+2x=0 \\ \\ x^2+y^2-2x=0\end{cases}

Abbiamo:

\small \begin{cases} \boxed{2x-1=0} \quad \rightarrow \quad x=\dfrac{1}{2} \\ \\ x^2+y^2-2x=0 \quad \rightarrow \quad y^2=2x-x^2 \quad \rightarrow y^2=1-\dfrac{1}{4} \quad \rightarrow y=\pm \dfrac{\sqrt{3}}{2}\end{cases}

Otteniamo così dall’intersezione delle due circonferenze i punti:

A=\left(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right); \qquad B=\left( \dfrac{1}{2}, -\dfrac{\sqrt{3}}{2}\right)

Questi sono i punti base del fascio di circonferenze in esame.

L’asse radicale, ovvero la retta che passa per i punti {A} e {B} ha per equazione quella evidenziata nel riquadro nel sistema:

r_{AB}:2x-1=0

ovvero, dividendo tutti i termini per {2}:

r_{AB}:x-\dfrac{1}{2}=0 \quad \Rightarrow \quad x=\dfrac{1}{2}

Tale equazione si ottiene in alternativa anche a partire dai due punti {A} e {B}. Poiché i due punti sono infatti allineati verticalmente (stessa ascissa), la retta che passa per essi è la retta verticale {x=\dfrac{1}{2}}, ove al secondo membro abbiamo l’ascissa in comune ai due punti.

Ora, l’asse centrale è perpendicolare all’asse radicale ed inoltre passa per il centro delle circonferenze generatrici. Poiché l’ordinata del centro di tali circonferenze è {0} (vedi i coefficienti {b_1} e {b_2} nelle rispettive equazioni), l’asse centrale avrà equazione:

r_{C}: y=0

e corrisponde quindi all’asse {x}.

L’equazione del fascio di circonferenze dato si può scrivere a partire dalle equazioni delle circonferenze {\mathscr{C}_1} e {\mathscr{C}_2}:

x^2+y^2-1+k(x^2+y^2-2x)=0

Volendo ricondurre tale equazione alla forma **, basta infine sviluppare il prodotto e quindi raccogliere rispetto ai termini in {x^2, y^2} e {y}:

\begin{align*} &x^2+y^2-1+kx^2+ky^2-2kx=0; \\ \\ & x^2+kx^2+y^2+ky^2-2kx-1=0;\\ \\ & (1+k)x^2+(1+k)y^2-2kx-1=0\end{align*}

Osserviamo come ulteriore alternativa che l’equazione dell’asse radicale si può anche ottenere dall’equazione del fascio ponendo {k=-1}:

\begin{align*} &  (1-1)x^2+(1-1)y^2+2x-1=0 \quad \Rightarrow \:2x-1=0 \quad \Rightarrow \\ \\ &   x-\dfrac{1}{2}=0 \quad \Rightarrow \: x=\dfrac{1}{2} \end{align*}

Infine, possiamo esprimere l’equazione del fascio anche come combinazione dell’equazione di una delle due circonferenze generatrici e dell’equazione dell’asse radicale. Ad esempio:

\underbrace{x^2+y^2-1}_{\mathscr{C}_1}+h\underbrace{\left(x-\dfrac{1}{2}\right)}_{r_{AB}}=0

ovvero calcolando il prodotto:

x^2+y^2-1+hx-\dfrac{1}{2}h=0

e infine, riordinando i termini e riconducendo l’equazione alla forma intera:

2x^2+2y^2+2hx-h-2=0

Come possiamo vedere dalla seguente figura, l’asse centrale del fascio coincide con l’asse delle {x} (il quale ha equazione {y=0}), mentre l’asse radicale è dato dalla retta verticale {x=\dfrac{1}{2}}:

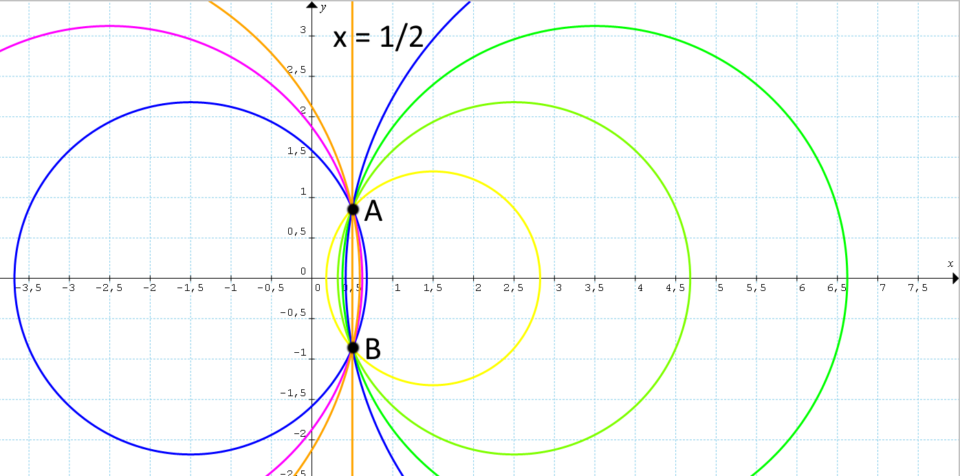
In figura abbiamo ovviamente rappresentato soltanto alcune circonferenze del fascio, secondo una scelta casuale.

La possibilità di poter esprimere un fascio di circonferenze secanti mediante la combinazione lineare dell’equazione di una delle circonferenze generatrici e dell’equazione dell’asse radicale risulta comoda quando si deve scrivere l’equazione di un fascio di circonferenze a partire dai suoi punti base, come mostra il seguente esempio.

Esempio 2

Scrivere l’equazione del fascio di circonferenze avente per punti base {A=(2,3)} e {B=(-1,5)}.

In teoria potremmo scrivere l’equazione del fascio a partire da due circonferenze generatrici {\mathscr{C}_1} e {\mathscr{C}_2}. Tuttavia, ciò richiede di dover scrivere le equazioni di due circonferenze tali da passare per i punti {A} e {B}. Ma, dato che per due punti passano infinite circonferenze, dovremmo imporre un’ulteriore condizione a nostra scelta.

Più pratico risulta allora scrivere l’equazione della retta passante per i due punti {A} e {B} (l’asse radicale del fascio) e l’equazione di una sola circonferenza, avente ad esempio, nel caso più semplice, come diametro il segmento di estremi {A} e {B}.

Per la retta per {A} e {B} basta utilizzare la formula della retta passante per due punti, sostituendo i valori delle coordinate dei punti {A} e {B}:

\dfrac{y-y_A}{y_B-y_A}=\dfrac{x-x_A}{x_B-x_A}

Si ha:

\begin{align*} &\dfrac{y-3}{5-3}= \dfrac{x-2}{-1-2}; \\ \\ & y=2 \cdot \dfrac{x-2}{-3}+3;\\ \\ & r_{AB}:  y=-\dfrac{2}{3}x+\dfrac{13}{3}\end{align*}

ovvero in forma implicita:

r_{AB}: \dfrac{2}{3}x+y-\dfrac{13}{3}=0  \quad \Rightarrow \quad r_{AB}: 2x+3y-13=0

Per la circonferenza di diametro avente estremi {A} e {B}, abbiamo che il centro è dato dal punto medio del segmento {\overline{AB}}:

M_{AB}=\left( \dfrac{x_A+x_B}{2}, \dfrac{y_A+y_B}{2}\right)=\left( \dfrac{2-1}{2}, \dfrac{3+5}{2}\right)=\left( \dfrac{1}{2}, 4\right)=C

Per il raggio:

\begin{align*} & r=\overline{AM_{AB}}=\sqrt{(x_A-x_{M_{AB}})^2+(y_A-y_{M_{AB}})^2}=\\ \\ & =\sqrt{\left( 2-\dfrac{1}{2}\right)^2+\left(3-4 \right)^2}= \sqrt{\dfrac{9}{4}+1}=\dfrac{\sqrt{13}}{2}\end{align*}

Così l’equazione della circonferenza il cui diametro ha per estremi i punti {A} e {B} è, nella forma con centro e raggio:

\left(x-\dfrac{1}{2}\right)^2+\left( y-4\right)^2=\dfrac{13}{4}

Per riscrivere l’equazione in forma canonica in alternativa al calcolo dei quadrati possiamo ricavare i coefficienti {a,b,c}:

a=-2x_C=-2 \cdot \dfrac{1}{2}=-1; \qquad b=-2y_C=-2 \cdot 4 = -8

c=x_C^2+y_C^2-r^2=\dfrac{1}{4}+16-\dfrac{13}{4}=\dfrac{64-12}{4}=13

Di conseguenza, l’equazione in forma canonica della circonferenza è:

\mathscr{C}_1: x^2+y^2-x-8y+13=0

A questo punto non resta che scrivere l’equazione del fascio come combinazione lineare delle equazioni di {\mathscr{C}_1} e di {r_{AB}}:

x^2+y^2-x-8y+13+h\left( 2x+3y-13\right) = 0

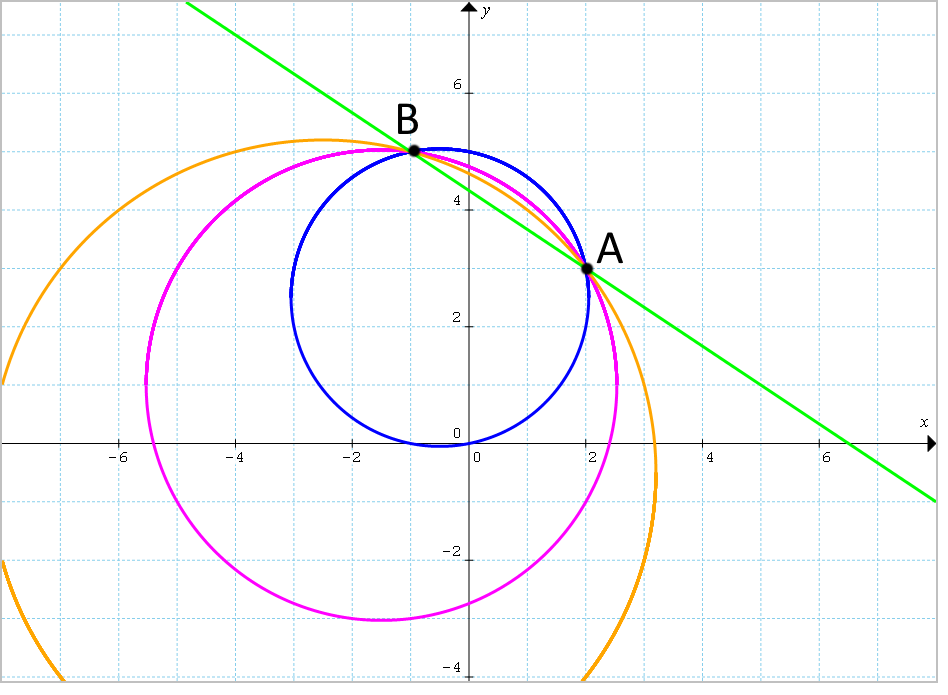
Concludiamo determinando l’equazione dell’asse centrale del fascio.

Ricordiamo anzitutto che l’asse centrale è perpendicolare all’asse radicale e passa per i centri delle circonferenze. Il centro {C=\left( \dfrac{1}{2}, 4\right)} di una circonferenza generatrice è noto. Per il coefficiente angolare dell’asse radicale, basta considerare l’equazione dell’asse radicale in forma esplicita che abbiamo scritto in precedenza:

r_{AB}: \dfrac{2}{3}x+y-\dfrac{13}{3}=0 

da essa ricaviamo in modo immediato un valore del coefficiente angolare per l’asse radaicale uguale a {\dfrac{2}{3}}.

Ma a questo punto per scrivere l’equazione dell’asse centrale abbiamo tutto ciò che ci serve: un punto ad esso appartenente (il centro {C} di una circonferenza generatrice) e il suo coefficiente angolare (l’inverso del reciproco del coefficiente angolare dell’asse radicale, data la relazione di perpendicolarità tra i due).

Abbiamo quindi per l’equazione dell’asse centrale:

r_{C}: y-4=-\dfrac{1}{-\frac{2}{3}}\left(x-\dfrac{1}{2}\right)

ovvero:

r_{C}:y=\dfrac{3}{2}x+\dfrac{13}{4}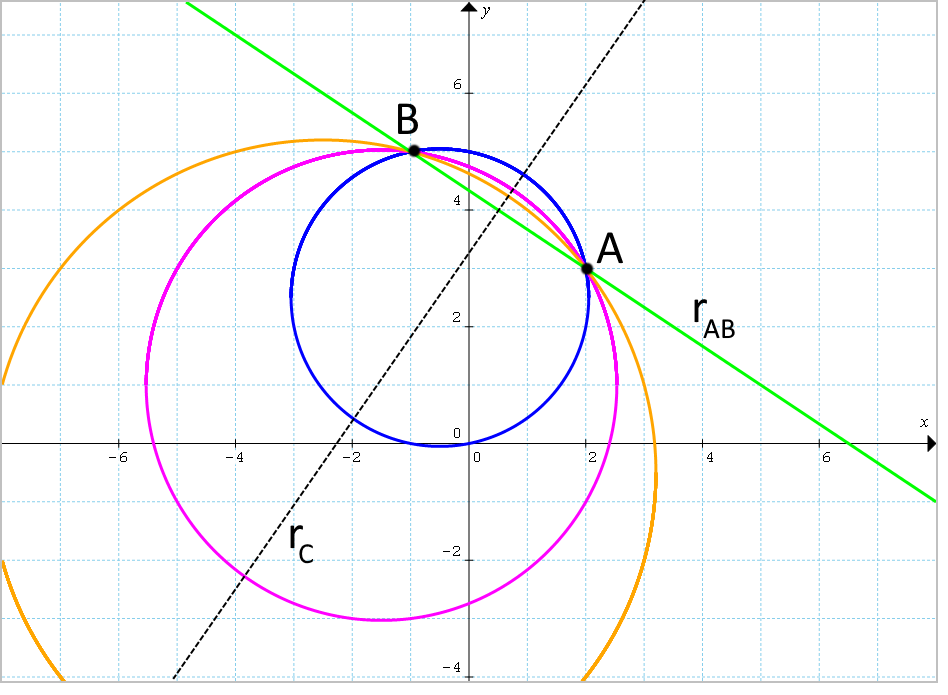

Esempio 3

Determinare i punti base del seguente fascio di circonferenze con generatrici secanti:{(1+k)x^2+(1+k)y^2+(2-2k)x+(2-2k)y+k-3=0}

Ponendo {k=0} otteniamo l’equazione di una delle circonferenze generatrici, ovvero {\mathscr{C}_1}:

\small \begin{align*} &(1+k)x^2+(1+k)y^2+(2-2k)x+(2-2k)y+k-3=0, \quad \text{con} \: k=0 \\ \\ & \Rightarrow \mathscr{C}_1:  x^2+y^2+2x+2y-3=0\end{align*}

Come ormai sappiamo l’asse radicale si ottiene per {k=-1}, ovvero per il valore di {k} che fa sparire i termini di secondo grado dall’equazione del fascio:

\small \begin{align*} &(1+k)x^2+(1+k)y^2+(2-2k)x+(2-2k)y+k-3=0, \quad \text{con} \: k=-1 \\ \\ & \Rightarrow r_{AB}: 4x+4y-4=0 \quad \Rightarrow \quad r_{AB}: x+y-1=0\end{align*}

Ora per determinare i punti base non resta che intersecare la circonferenza {\mathscr{C}_1} con la retta {r_{AB}}. Ricerchiamo infatti i due punti per i quali passano le circonferenze del fascio (compresa quindi una delle generatrici) e per i quali passa allo stesso tempo la retta corrispondente all’asse radicale. Abbiamo:

\begin{cases}\mathscr{C}_1:   x^2+y^2+2x+2y-3=0\\ \\  r_{AB}:x+y-1=0 \end{cases}

Esplicitiamo la {x} dalla seconda equazione:

\begin{cases}  x^2+y^2+2x+2y-3=0\\ \\ x=1-y \end{cases}

Sostituiamo l’espressione ottenuta per {x} nella prima equazione a sistema, ottenendo un’equazione di secondo grado nella sola incognita {y}, che sappiamo risolvere:

\begin{align*} & (1-y)^2+y^2+2(1-y)+2y-3=0; \\ \\ & 1-2y+y^2+y^2+2-\cancel{2y}+\cancel{2y}-3=0; \\ \\ & 2y^2-2y=0\end{align*}

Risolviamo l’equazione di secondo grado (si tratta di un’equazione spuria):

2y(y-1)=0 \quad \Rightarrow \quad y = 0 \quad \vee \quad y=1

Otteniamo così i due valori {y_1=0} e {y_2=1}. Ora riprendendo la seconda equazione a sistema, ovvero l’equazione {x=1-y}, sostituendo i valori appena ottenuti per l’incognita {y} otteniamo i seguenti valori per l’incognita {x}:

x_1=1; \qquad x_2=0

Di conseguenza, otteniamo dall’intersezione della circonferenza {\mathscr{C}_1} e della retta {r_{AB}} i punti:

A=(1,0), \qquad B=(0,1)

Come ulteriore esercizio, riprendiamo l’equazione dell’asse radicale dell’esempio appena svolto:

r_{AB}:x+y-1=0 

In forma esplicita diviene:

r_{AB}: y=-x+1

da cui abbiamo il coefficiente angolare {m_{AB} = -1}.

La circonferenza generatrice {\mathscr{C}_1} ha centro {C=(-1,-1)}. Infatti data la sua equazione:

\mathscr{C}_1:  x^2+y^2+2x+2y-3=0

dalle formule per ricavare le coordinate del centro a partire dai coefficienti dell’equazione della circonferenza in forma canonica ricaviamo:

x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot 2=-1; \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2}\cdot2=-1

Di conseguenza per l’equazione dell’asse centrale, perpendicolare all’asse radicale e passante per {C}, abbiamo:

r_{C}: y+1=1\cdot(x+1)

da cui:

r_{C}:y=x

e questa è in conclusione l’equazione dell’asse centrale del fascio, ovvero l’equazione della retta passante per tutti i centri delle circonferenze del fascio.

Precisiamo ancora che un fascio di circonferenze è costituito da infinite circonferenze, ciascuna delle quali si ottiene per un certo valore del parametro reale k oppure h (il parametro utilizzato dipende da come è scritta l’equazione del fascio). Nelle figure rappresentiamo soltanto qualche circonferenza poiché ovviamente sarebbe impossibile disegnarne infinite. Ma non dimentichiamo mai che per ogni valore del parametro reale si ottiene un’equazione della forma {x^2+y^2+ax+by+c=0}. Poi a tale equazione potrà corrispondere o meno una circonferenza reale non degenere, ma per le proprietà dell’insieme dei numeri reali le circonferenze del fascio sono comunque infinite.

Fascio di circonferenze tangenti

Abbiamo visto che a partire da due circonferenze secanti è possibile costruire un fascio di circonferenze tutte secanti, ovvero tutte passanti per i punti base del fascio. Allo stesso modo, partendo da due circonferenze tangenti in un dato punto {A} ad una retta {t}, è possibile costruire un fascio di circonferenze caratterizzato da infinite circonferenze tutte tangenti nello stesso punto {A} alla medesima retta {t}.

Consideriamo allora due circonferenze {\mathscr{C}_1} e {\mathscr{C}_2}, tangenti nel punto {A} ad una stessa retta {t}

Il fascio di circonferenze avente per generatrici le circonferenze {\mathscr{C}_1} e {\mathscr{C}_2} è dato da tutte le circonferenze tali da essere tangenti nello stesso punto {A} alla medesima retta {t} (in generale non necessariamente verticale come in figura, ma avente pendenza qualsiasi).

In questo caso abbiamo un solo punto base del fascio, dato dal punto di tangenza {A}. La retta tangente {t} è l’asse radicale del fascio.

Come nel precedente caso di un fascio di circonferenze avente generatrici secanti, anche nel caso di un fascio di circonferenze con generatrici tangenti è possibile ottenere l’equazione del fascio a partire dalla combinazione lineare delle equazioni delle circonferenze generatrici, oppure a partire dall’equazione di una delle due circonferenze generatrici e dall’equazione dell’asse radicale del fascio (ovvero dall’equazione della retta tangente {t}).

Così date le due circonferenze {\mathscr{C}_1} e {\mathscr{C}_2}, tangenti in {A} alla retta {t} ed aventi equazioni:

\small \mathscr{C}_1: x^2+y^2+a_1x+b_1y+c_1=0; \qquad \mathscr{C}_2:x^2+y^2+a_2x+b_2y+c_2=0

l’equazione del fascio di circonferenze da esse generato ha equazione, come nel caso di un fascio generato da circonferenze secanti:

\small (1+k)x^2+(1+k)y^2+(a_1+ka_2)x+(b_1+kb_2)y+c_1+kc_2=0 \qquad (**)

Inoltre, seguendo ragionamenti del tutto simili a quelli fatti in precedenza, la retta tangente {t} ha equazione:

t:(a_1-a_2)x+(b_1-b_2)y+c_1-c_2=0

e tale equazione si ottiene ancora ponendo {k=-1} nell’equazione del fascio.

Inoltre, è possibile esprimere l’equazione del fascio generato dalle circonferenze {\mathscr{C}_1} e {\mathscr{C}_2} anche come:

\small x^2+y^2+a_1x+b_1y+c_1+h[(a_1-a_2)x+(b_1-b_2)y+c_1-c_2]=0 \qquad (***)

Infine, è anche possibile esprimere l’equazione del fascio di circonferenze con generatrici tangenti come:

\small x^2+y^2+a_1x+b_1y+c_1+k(x^2+y^2+a_2x+b_2y+c_2)=0 \qquad (****)

ritrovando di nuovo una forma già vista nel caso dei fasci di circonferenze con generatrici secanti.

Prima di passare agli esempi, ricordiamo che dalla geometria elementare la retta tangente ad una circonferenza in un punto {A} è perpendicolare alla retta passante per il centro della circonferenza e lo stesso punto {A}. Di conseguenza, la retta perpendicolare all’asse radicale del fascio e passante per il punto di tangenza {A} è il luogo dei centri delle circonferenze del fascio (ovvero l’asse centrale del fascio). Ciò significa che i centri delle circonferenze del fascio appartengono tutti a tale retta.

Esempio 4 (fascio di circonferenze tangenti)

Scrivere l’equazione del fascio di circonferenze generato dalle circonferenze {\mathscr{C}_1: x^2+y^2-2x+6y-30=0} e {\mathscr{C}_2: x^2+y^2+2x-6y+10=0}.

Vediamo anzitutto quali eventuali punti in comune hanno le circonferenze tra loro. Impostiamo il sistema contenente le rispettive equazioni:

\begin{cases} x^2+y^2-2x+6y-30=0 \\ \\ x^2+y^2+2x-6y+10=0 \end{cases}

Risolviamo per riduzione il sistema, sostituendo alla prima equazione una nuova equazione che si ottiene sottraendo membro a membro alla prima equazione a sistema la seconda:

\begin{cases} -2x+6y-30-2x+6y-10=0 \\ \\ x^2+y^2+2x-6y+10=0\end{cases}

si ha:

\begin{cases} -4x+12y-40 = 0 \quad \rightarrow \quad -x+3y-10=0 \quad \rightarrow \quad x=3y-10 \\ \\  x^2+y^2+2x-6y+10=0 \end{cases}

Sostituendo l’espressione {3y-10} nella seconda equazione a sistema otteniamo un’equazione di secondo grado nella sola incognita {y}:

\begin{align*} & (3y-10)^2+y^2+2(3y-10)-6y+10=0; \\ \\ & 9y^2-60y+100+y^2+\cancel{6y}-20-\cancel{6y}+10=0;\\ \\ & 10y^2-60y+90=0;\\ \\ & y^2-6y+9=0\end{align*}

Risolvendo l’equazione di secondo grado:

y_{1,2} = \dfrac{3 \pm \sqrt{(-3)^2-1 \cdot 9}}{1}=3\pm 0=3

Otteniamo così due soluzioni reali e coincidenti, che a lato pratico forniscono un solo valore per la coordinata {y}. Sostituendo il valore ottenuto nell’equazione a sistema {x=3y-10} otteniamo per la coordinata {x}:

x=3y-10=3 \cdot3 - 10 = -1

Così le due circonferenze {\mathscr{C}_1} e {\mathscr{C}_2} si intersecano nel solo punto {A=(-1, 3)}, che è il punto base del fascio in esame.

Con considerazioni del tutto simili a quelle fatte nel caso dei fasci di circonferenze con generatrici secanti, l’equazione dell’asse radicale è individuabile dal sistema come:

x=3y-10 \quad \rightarrow \quad t:x-3y+10=0

e corrisponde alla retta tangente alle circonferenze nel punto base {A=(-1,3)}. Infatti, tale equazione si ottiene imponendo che le due circonferenze si intersechino, e di conseguenza questa è soddisfatta dalle coordinate del punto di intersezione (in questo caso punto di tangenza) tra le due circonferenze.

Ora, la forma più semplice grazie alla quale esprimere l’equazione del fascio di circonferenze dato è quella del tipo ****:

 \small x^2+y^2-2x+6y-30+k(x^2+y^2+2x-6y+10)=0

Tra l’altro, ponendo {k=-1} da tale equazione ritroviamo l’equazione dell’asse radicale (retta tangente alle circonferenze del fascio nel punto base):

\begin{align*} & \cancel{x^2}+\cancel{y^2}-2x+6y-30-\cancel{x^2}-\cancel{y^2}-2x+6y-10=0; \\ \\ &-4x+12y-40=0;\\ \\ & t: x-3y+10=0  \end{align*}

Volendo scrivere l’equazione del fascio nelle forme ** e *** abbiamo rispettivamente:

\small \begin{align*} &  x^2+y^2-2x+6y-30+k(x^2+y^2+2x-6y+10)=0; \\ \\ & x^2+y^2-2x+6y-30+kx^2+ky^2+2kx-6ky+10k=0;\\ \\ &\boxed{ (1+k)x^2+(1+k)y^2+(-2+2k)x+(6-6k)y-30+10k=0}\end{align*}

e, utilizzando ad esempio l’equazione della circonferenza {\mathscr{C}_1}:

x^2+y^2-2x+6y-30+h(x-3y+10)=0

Osserviamo infine che le circonferenze del fascio hanno centri che appartengono tutti alla retta perpendicolare a {t} e passante per il punto base {A}. Tale retta è l’asse centrale del fascio. Indicando con {r_C} tale retta abbiamo:

r_C: y-y_A=-\dfrac{1}{m_t} (x-x_A)

ove {m_t} è il coefficiente angolare dell’asse radicale del fascio e {x_A} e {y_A} sono le coordinate del punto base {A}.

Riprendiamo per comodità l’equazione dell’asse radicale, ovvero della retta {t}:

t: x-3y+10=0 

Esprimiamola in forma esplicita:

t:y=\dfrac{1}{3}x+\dfrac{10}{3}

Abbiamo {m_t = \dfrac{1}{3}} e quindi per l’equazione dell’asse centrale precedentemente scritta otteniamo, sostituendo i valori:

r_C:y-3=-3(x+1) \quad \Rightarrow \quad r_C:y=-3x

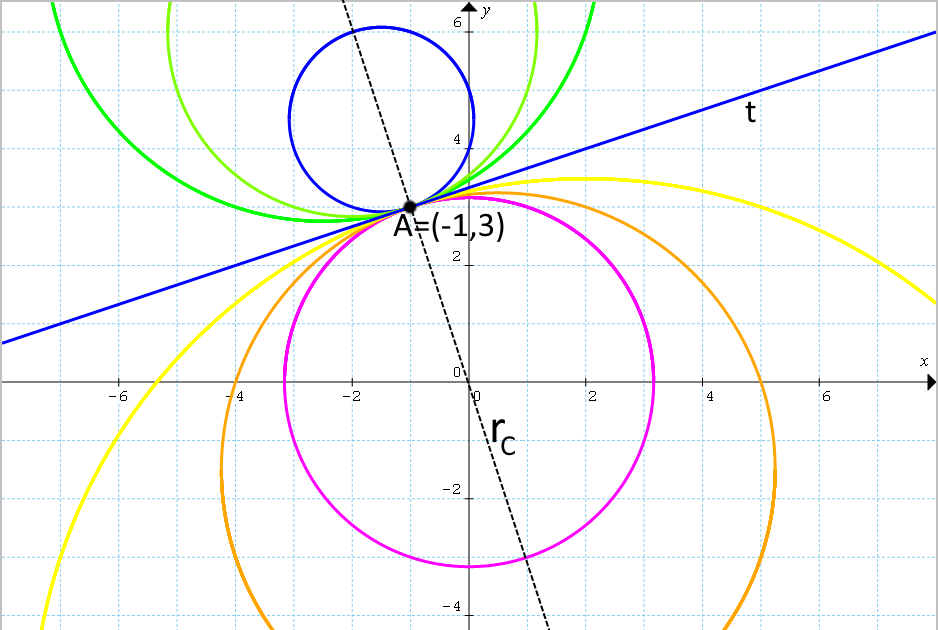
Esempio 5

Studiare il fascio di circonferenze di equazione {x^2+y^2-3(2-k)x+4ky-16-34k=0}.

Calcolando i prodotti al primo membro dell’equazione del fascio, riordinando i termini e quindi eseguendo un raccoglimento parziale per {k} si ha:

\begin{align*} & x^2+y^2-3(2-k)x+4ky-16-34k=0 ;\\ \\ &x^2+y^2-6x+3kx+4ky-16-34k=0;\\ \\ & x^2+y^2-6x-16+3kx+4ky-34k=0; \\ \\ &x^2+y^2-6x-16+k(3x+4y-34)=0\end{align*}

e quindi più propriamente, cambiando il nome del parametro secondo le convenzioni sin qui adottate (l’equazione è della forma ***):

x^2+y^2-6x-16+h(3x+4y-34)=0

Abbiamo così riscritto l’equazione del fascio come combinazione lineare tra l’equazione di una delle circonferenze generatrici (che indicheremo ad esempio con {\mathscr{C}_1}) e l’equazione dell’asse radicale, che indicheremo genericamente con {r}:

\mathscr{C}_1: x^2+y^2-6x-16=0, \qquad r:3x+4y-34=0

A questo punto impostiamo un sistema contenente le due equazioni appena scritte, in modo da ricercare gli eventuali punti di intersezione tra la circonferenza generatrice e l’asse radicale:

\begin{cases} x^2+y^2-6x-16=0 \\ \\ 3x+4y-34 = 0\end{cases}

Procediamo per sostituzione isolando ad esempio la variabile {x} dalla seconda equazione:

\begin{cases}  x^2+y^2-6x-16=0\\ \\ 3x+4y-34 = 0 \quad \rightarrow x=\dfrac{34}{3}-\dfrac{4}{3}y\end{cases}

quindi sostituiamo l’espressione ottenuta per la variabile {x} nella prima equazione a sistema (consideriamola separatamente):

\begin{align*} &\left( \dfrac{34}{3}-\dfrac{4}{3}y\right)^2+y^2-6\left( \dfrac{34}{3}-\dfrac{4}{3}y\right)-16=0;\\ \\ & \dfrac{34^2}{9}-\dfrac{8\cdot 34}{9}y+\dfrac{16}{9}y^2+y^2-\dfrac{6 \cdot 34}{3}+\dfrac{24}{3}y-16=0;\\ \\ & \dfrac{25}{9}y^2+\left( \dfrac{-272+72}{9}\right)y+\dfrac{1156-612-144}{9}=0;\\ \\ & \dfrac{25}{9}y^2-\dfrac{200}{9}y+\dfrac{400}{9}=0;\\ \\ & y^2-8y+16=0 \end{align*}

Risolvendo l’equazione di secondo grado otteniamo per {y}:

y_{1,2}=4 \pm \sqrt{(-4)^2-16}=4

Così ai fini pratici otteniamo per {y} il solo valore {y=4}. Sostituendo tale valore nella seconda equazione a sistema otteniamo per {x}:

x=\dfrac{34}{3}-\dfrac{4}{3}y=\dfrac{34}{3}-\dfrac{16}{3}=\dfrac{18}{3}=6

Così dall’intersezione delle equazioni della circonferenza generatrice e dell’asse radicale otteniamo il punto {A=(6,4)}, che è il punto base del fascio. Avendo ottenuto un solo punto base, concludiamo che il fascio di circonferenze in esame è dato da circonferenze tutte tangenti nel punto {A} alla retta di equazione:

t:3x+4y-34=0

ovvero in forma esplicita:

t:y=-\dfrac{3}{4}x+\dfrac{34}{4}

Questa retta è l’asse radicale del fascio.

Infine per il luogo dei centri delle circonferenze (o asse centrale) abbiamo, come visto nell’esempio precedente:

r_C:  y-y_A=-\dfrac{1}{m_t}(x-x_A)

ovvero:

r_C:y-4 = -\dfrac{1}{-\frac{3}{4}} (x-6) \quad \Rightarrow \quad r_C:y=\dfrac{4}{3}x-4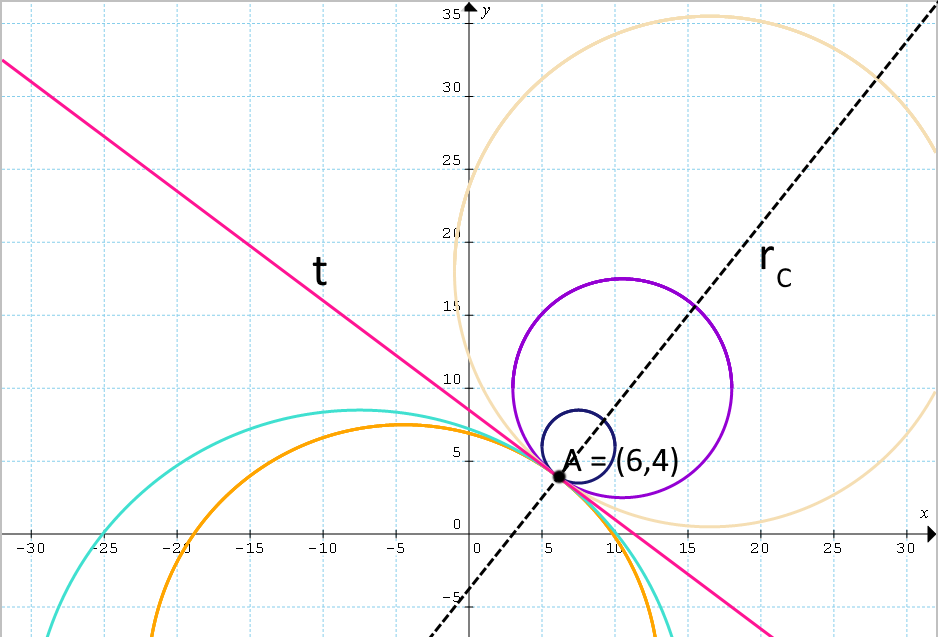

Fasci di circonferenze concentriche

Consideriamo due circonferenze {\mathscr{C}_1} e {\mathscr{C}_2} aventi equazioni:

\small \mathscr{C}_1:x^2+y^2+ax+by+c_1=0; \qquad \mathscr{C}_2:x^2+y^2+ax+by+c_2=0

Osserviamo che le due circonferenze hanno in comune i coefficienti {a} e {b} dei termini in {x} e {y}. Ma come visto nelle precedenti lezioni per le coordinate del centro {C} di una circonferenza valgono le formule:

x_C=-\dfrac{1}{2}a; \qquad y_C=-\dfrac{1}{2}b

ovvero le coordinate del centro dipendono dai coefficienti {a} e {b} dell’equazione in forma canonica di una circonferenza.

Ora, poiché nelle equazioni delle circonferenze {\mathscr{C}_1} e {\mathscr{C}_2} i coefficienti {a} e {b} sono gli stessi, concludiamo che le due circonferenze sono concentriche, ovvero hanno gli stessi centri.

Così, se a partire dalle circonferenze {\mathscr{C}_1} e {\mathscr{C}_2} costruiamo un fascio di circonferenze, esso sarà dato da circonferenze tutte concentriche fra loro.

Riprendendo l’equazione del fascio di circonferenze nella forma **** si ha per il caso in esame la seguente equazione del fascio di circonferenze concentriche:

x^2+y^2+ax+by+c_1+k(x^2+y^2+ax+by+c_2)=0

ovvero:

x^2+y^2+ax+by+c_1+kx^2+ky^2+kax+kby+kc_2=0

e quindi, raccogliendo opportunamente:

(1+k)x^2+(1+k)y^2+(a+ka)x+(b+kb)y+c_1+kc_2=0

e infine, raccogliendo ove possibile all’interno delle parentesi tonde e portando il fattore messo in evidenza al di fuori delle parentesi:

(1+k)x^2+(1+k)y^2+a(1+k)x+b(1+k)y+c_1+kc_2=0 \qquad (⁑)

L’equazione appena scritta rappresenta un fascio di circonferenze concentriche. Il centro comune a tutte le circonferenze del fascio è dato da:

C=\left( -\dfrac{1}{2}a, -\dfrac{1}{2}b\right)

Infatti posto {k \neq -1} dividendo tutti i termini per {1+k} l’equazione ⁑ diviene:

x^2+y^2+ax+by+\dfrac{c_1+kc_2}{1+k}=0

e rappresenta al variare del parametro {k} delle circonferenze di centro comune {C=\left( -\dfrac{1}{2}a, -\dfrac{1}{2}b\right)}. Infatti, tutte le circonferenze hanno gli stessi coefficienti dei termini in {x} ed {y}, sempre uguali ad {a} e {b}.

Così, l’equazione di un fascio di circonferenze concentriche è riconoscibile dal fatto che i coefficienti dei termini in {x} e {y} non dipendono dal parametro.

Prima di passare agli esempi, consideriamo che in generale non è particolarmente agevole stabilire per quale insieme di valori del parametro reale si ottengono, a partire dall’equazione di un fascio di circonferenze generico, delle circonferenze reali non degeneri. Nel caso invece dei fasci di circonferenze concentriche, poiché i coefficienti dei termini in {x} e {y} non dipendono dal parametro, ciò è invece più fattibile, specialmente nel caso in cui i coefficienti dei termini in {x^2} e {y^2} siano unitari, come mostra il seguente esempio.

Esempio 6 (fascio di circonferenze concentriche)

Studiare il fascio di circonferenze di equazione {x^2+y^2+2x-2y+\dfrac{1-2k}{1+k}=0}. Stabilire inoltre per quali valori reali del parametro {k} si ottengono circonferenze reali non degeneri.

Poiché i coefficienti dei termini in {x} e {y} non dipendono dal parametro, le circonferenze del fascio condividono tutte lo stesso centro. Riconosciamo che l’equazione data è quella di una fascio poiché il termine noto dipende dal parametro {k}:

x^2+y^2+2x-2y+\underbrace{\dfrac{1-2k}{1+k}}_{\substack{\text{termine} \\ \text{noto} \: c}}=0

Nell’equazione abbiamo {a=2} e {b=-2}. Il centro comune a tutte le circonferenze del fascio è dunque:

C=\left( -\dfrac{1}{2}a, -\dfrac{1}{2}b\right)=(-1,1)

Ora, ricordiamo la condizione per la quale una circonferenza con equazione in forma canonica {x^2+y^2+ax+by+c=0} è reale non degenere:

\dfrac{a^2}{4}+\dfrac{b^2}{4}-c>0

Nel caso dell’equazione del fascio in esame tale condizione diviene:

\dfrac{2^2}{4}+\dfrac{(-2)^2}{4}-\dfrac{1-2k}{1+k} > 0

Si tratterà così di risolvere la disequazione appena scritta rispetto a {k}. Siamo nel caso di una disequazione fratta di primo grado. Cominciamo riducendo i termini a denominatore comune:

\dfrac{4(1+k)+4(1+k)-4+8k}{4(1+k)}> 0

Eseguendo un raccoglimento al numeratore:

\dfrac{\cancel{4}(1+k+1+k-1+2k)}{\cancel{4}(1+k)}>0

otteniamo:

\dfrac{4k+1}{1+k} > 0

Effettuiamo lo studio dei segni del numeratore e del denominatore:

Si ha che la disequazione è verificata per:

k < -1 \quad \vee \quad k > -\dfrac{1}{4}

e per tali valori del parametro {k} si ottengono dall’equazione del fascio data delle circonferenze reali non degeneri.

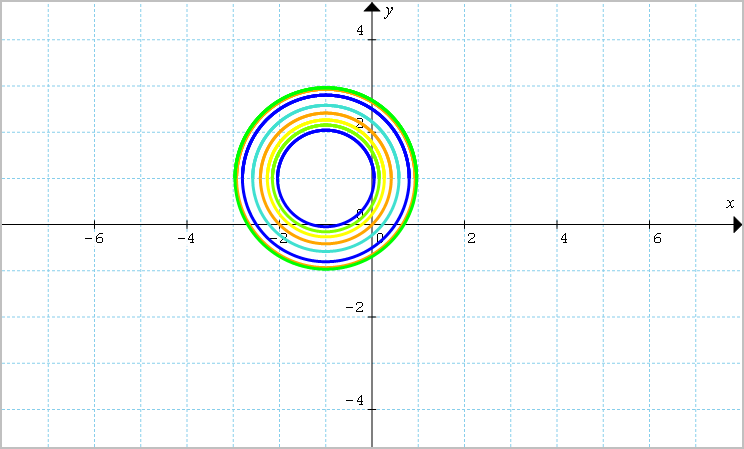
Fasci di circonferenze senza punti in comune e non concentriche

L’ultimo caso è quello relativo al fascio di circonferenze le cui generatrici non hanno punti in comune e non hanno nemmeno il centro in comune. In altre parole, le circonferenze generatrici e più in generale tutte le circonferenze del fascio non sono né tangenti e nemmeno secanti e non sono inoltre concentriche.

Anche in questo caso l’equazione del fascio si costruisce come combinazione lineare delle equazioni delle circonferenze generatrici. Come nei casi precedenti inoltre abbiamo l’asse radicale e l’asse centrale del fascio.

L’asse radicale è ancora definito come la retta di equazione:

(a_1-a_2)x+(b_1-b_2)y+c_1-c_2=0

e l’asse centrale è come negli altri casi la retta che passa per i centri delle circonferenze del fascio. In particolare, la sua equazione corrisponde a quella della retta che congiunge i centri delle circonferenze generatrici del fascio.

Inoltre, l’asse radicale e l’asse centrale risultano ancora perpendicolari tra loro. Infine, fasci di questo tipo sono privi di punti base.

Dimostrazione del fatto che l’asse centrale di un fascio di circonferenze secanti è perpendicolare all’asse radicale (facoltativa)

Per concludere la lezione riportiamo la dimostrazione relativa al fatto che in un fascio di circonferenze secanti l’asse centrale è perpendicolare all’asse radicale. Precisiamo che tale dimostrazione è del tutto facoltativa e che l’espressione che otterremo per l’equazione dell’asse radicale di un generico fascio di circonferenze secanti non è assolutamente da imparare a memoria.

Il primo passo per dimostrare la perpendicolarità tra asse centrale ed asse radicale consiste nel ricavare l’equazione in forma esplicita dell’asse centrale. In tal modo, sarà possibile ricavare da essa un’espressione per il coefficiente angolare dell’asse centrale.

Ora, per ottenere l’espressione generica dell’equazione dell’asse centrale di una fascio di circonferenze secanti, partiamo dalle coordinate del centro delle circonferenze generatrici. Per come abbiamo definito in precedenza le corrispondenti equazioni, per le due circonferenze generatrici {\mathscr{C}_1} e {\mathscr{C}_2} abbiamo rispettivamente le coordinate dei centri:

C_1=\left( -\dfrac{1}{2}a_1, -\dfrac{1}{2}b_1\right); \qquad C_2=\left( -\dfrac{1}{2}a_2, -\dfrac{1}{2}b_2\right)

Per la formula della retta passante per due punti, l’equazione dell’asse centrale del fascio, ovvero della retta che passa per i centri delle circonferenze generatrici, è:

\dfrac{y-y_{C_1}}{y_{C_2}-y_{C_1}}=\dfrac{x-x_{C_1}}{x_{C_2}-x_{C_1}}

ovvero sostituendo le espressioni delle coordinate dei centri in funzione dei coefficienti che compaiono nelle equazioni delle circonferenze generatrici (passaggi noiosi ma fattibili):

\small \begin{align*} &\dfrac{y+\dfrac{1}{2}b_1}{-\dfrac{1}{2}b_2-\left( -\dfrac{1}{2}b_1\right)}= \dfrac{x+\dfrac{1}{2}a_1}{-\dfrac{1}{2}a_2-\left(- \dfrac{1}{2}a_1\right)};\\ \\ & \dfrac{y+\dfrac{1}{2}b_1}{\dfrac{1}{2}(b_1-b_2)}=\dfrac{x+\dfrac{1}{2}a_1}{\dfrac{1}{2}(a_1-a_2)};\\ \\ & \dfrac{y+\dfrac{1}{2}b_1}{\dfrac{1}{2}(b_1-b_2)}-\dfrac{x+\dfrac{1}{2}a_1}{\dfrac{1}{2}(a_1-a_2)}=0;\\ \\ & \dfrac{\left( y+\dfrac{1}{2}b_1\right)(a_1-a_2)-\left( x+\dfrac{1}{2}a_1\right)(b_1-b_2)}{\dfrac{1}{2}(a_1-a_2)(b_1-b_2)}=0; \\ \\ &\dfrac{a_1y-a_2y+\cancel{\dfrac{1}{2}a_1b_1}-\dfrac{1}{2}a_2b_1-b_1x+b_2x-\cancel{\dfrac{1}{2}a_1b_1}+\dfrac{1}{2}a_1b_2}{\dfrac{1}{2}(a_1-a_2)(b_1-b_2)} =0; \\ \\ &\dfrac{(a_1-a_2)y+(b_2-b_1)x+\dfrac{1}{2}(a_1b_2-a_2b_1)}{\dfrac{1}{2}(a_1-a_2)(b_1-b_2)}=0 \\ \\ &\dfrac{2\cancel{(a_1-a_2)}y}{\cancel{(a_1-a_2)}(b_1-b_2)}= \dfrac{2\cancel{(b_1-b_2)}x}{(a_1-a_2)\cancel{(b_1-b_2)}}+\dfrac{a_2b_1-a_1b_2}{(a_1-a_2)(b_1-b_2)} \end{align*}

Osserviamo che per le semplificazioni eseguite si ha {a_1 \neq a_2 } e {b_1 \neq b_2}.

Proseguendo ancora i passaggi ed isolando la variabile {y}:

y= \dfrac{\cancel{2}(b_1-b_2)}{\cancel{2}(a_1-a_2)}x +\dfrac{(a_2b_1-a_1b_2)\cancel{(b_1-b_2)}}{2(a_1-a_2)\cancel{(b_1-b_2)}}

ovvero in conclusione:

y= \dfrac{b_1-b_2}{a_1-a_2}x +\dfrac{a_2b_1-a_1b_2}{2(a_1-a_2)}

Questa è l’equazione dell’asse centrale di un fascio di circonferenze secanti, dalla quale deduciamo la seguente espressione del coefficiente angolare per l’asse centrale:

m_C=\dfrac{b_1-b_2}{a_1-a_2}

Riprendiamo ora l’equazione dell’asse radicale:

(a_1-a_2)x+(b_1-b_2)y+c_1-c_2=0

Riduciamola alla forma esplicita:

y=\dfrac{(a_2-a_1)x+c_2-c_1}{(b_1-b_2)}

ovvero:

y=\dfrac{a_2-a_1}{b_1-b_2}x+\dfrac{c_2-c_1}{b_1-b_2}

da cui deduciamo per l’asse radicale il coefficiente angolare:

m_{ar}=\dfrac{a_2-a_1}{b_1-b_2}

Effettivamente confrontando i due coefficienti angolari si ha:

m_{C}=-\dfrac{1}{m_{ar}}

Ma ciò corrisponde alla condizione di perpendicolarità fra rette. Per cui effettivamente l’asse centrale e l’asse radicale di un fascio di circonferenze secanti sono tra loro perpendicolari.

Conclusioni

Questa lunga lezione sui fasci di circonferenze termina qui. E siamo anche arrivati alla conclusione di questo corso di lezioni sulla circonferenza per le scuole superiori.

Un saluto a tutti voi e buon proseguimento con SìMatematica!