Proponiamo in questa scheda una serie di esercizi di riepilogo sulla circonferenza, svolti e commentati. Gli esercizi si rivolgono agli studenti delle scuole superiori ed hanno per oggetto tutti i principali argomenti trattati nelle lezioni di geometria analitica relative alla retta e alla circonferenza.
Negli esercizi di riepilogo sulla circonferenza qui disponibili potremo allenarci sui seguenti argomenti:
- equazione della circonferenza (centro e raggio, forma canonica);
- come determinare le intersezioni tra una circonferenza e una retta;
- come scrivere l’equazione della retta tangente ad una circonferenza in un punto della circonferenza stessa;
- ancora, come determinare le equazioni delle rette tangenti ad una circonferenza condotte per un punto esterno;
- infine, le condizioni per determinare l’equazione di una circonferenza.
Per quanto riguarda invece i fasci di circonferenze rimandiamo alla scheda di esercizi dedicata, omettendo di presentare esercizi relativi ai fasci di circonferenze nei seguenti esercizi di riepilogo sulla circonferenza.
Mettiamoci a questo punto subito all’opera con gli esercizi di riepilogo sulla circonferenza di SìMatematica!
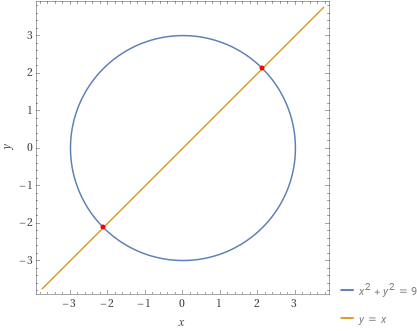
Esercizio 1
Determinare i punti di intersezione tra la circonferenza di centro l’origine e raggio uguale a {3} e la bisettrice del primo e terzo quadrante.
Per il primo di questa serie di esercizi di riepilogo sulla circonferenza, abbiamo un esercizio di livello base.
Cominciamo con lo scrivere l’equazione della circonferenza con centro l’origine e raggio {3}. Allo scopo dobbiamo utilizzare l’equazione della circonferenza con centro e raggio:
(x-x_C)^2+(y-y_C)^2=r^2
ove {x_C} ed {y_C} sono rispettivamente l’ascissa e l’ordinata del centro {C} della circonferenza.
Nel nostro caso la circonferenza è centrata nell’origine, e quindi abbiamo {C=(0,0)}. Inoltre, essendo {r=3} la precedente equazione sostituendo i valori diviene:
(x-0)^2+(y-0)^2=3^2
ovvero:
x^2+y^2=9
Ora, la bisettrice del primo e del terzo quadrante ha equazione:
y=x
Per determinare i punti di intersezione tra la circonferenza e la retta, dobbiamo mettere a sistema le rispettive equazioni:
\begin{cases} x^2+y^2=9 \\ \\ y=x\end{cases}Il sistema è del tipo non lineare ma si risolve agevolmente per sostituzione. In particolare, la seconda equazione afferma che le due variabili {x} ed {y} sono uguali fra loro. In questo caso, quindi, sostituendo nella prima equazione ad esempio ad ogni lettera {y} la lettera {x} otteniamo:
\begin{cases} x^2+x^2=9 \\ \\ y=x\end{cases}ovvero:
\begin{cases} 2x^2=9 \\ \\ y=x\end{cases}Risolvendo la prima equazione (si tratta di un’equazione di secondo grado) otteniamo:
2x^2=9 \quad \Rightarrow \quad x_{1,2}=\pm \sqrt{\dfrac{9}{2}} =\begin{cases} \dfrac{{3}}{\sqrt{2}} \\ \\ -\dfrac{3}{\sqrt{2}} \end{cases} Risostituendo i valori ottenuti nella seconda equazione a sistema ricaviamo due valori per l’incognita {y}:
y_1=\dfrac{3}{\sqrt{2}}; \qquad y_2=-\dfrac{3}{\sqrt{2}}Abbiamo così ottenuto due punti di intersezione tra la circonferenza e la retta. Il sistema infatti è determinato ed ha per soluzione due coppie di valori. E in ciascuna coppia abbiamo rispettivamente l’ascissa e l’ordinata di un punto di intersezione. In particolare, i due punti di intersezione sono:
A=\left( \dfrac{3}{\sqrt{2}}, \dfrac{3}{\sqrt{2}}\right); \qquad B=\left( -\dfrac{3}{\sqrt{2}}, -\dfrac{3}{\sqrt{2}}\right)Se preferite è possibile razionalizzare i valori delle coordinate, ottenendo:
A=\left( \dfrac{3\sqrt{2}}{2}, \dfrac{3\sqrt{2}}{2}\right); \qquad B=\left( -\dfrac{3\sqrt{2}}{2}, -\dfrac{3\sqrt{2}}{2}\right)L’esercizio è così concluso.
Proseguiamo gli esercizi di riepilogo sulla circonferenza con il seguente, nel quale ricaveremo una formula che consente di scrivere l’equazione canonica di una circonferenza avente per diametro un segmento di estremi dati.
Esercizio 2 (esercizi di riepilogo sulla circonferenza, esercizio teorico)
Scrivere una forma generale dell’equazione della circonferenza il cui diametro ha per estremi i punti {A=(x_A, y_A)} e {B=(x_B, y_B)}.
Se il diametro di una circonferenza ha per estremi i due punti {A} e {B}, ciò significa che il segmento {\overline{AB}} è il diametro della circonferenza. Ma allora, il centro della circonferenza coincide necessariamente con il punto medio del segmento. Se indichiamo il punto medio con {M=(x_M, y_M)}, per i valori delle sue coordinate si ha:
\begin{align*} &x_M=\dfrac{x_A+x_B}{2}=x_C; \qquad y_M=\dfrac{y_A+y_B}{2}=y_C\end{align*}Disponiamo a questo punto delle coordinate del centro della circonferenza in esame. Ma per poterne scrivere l’equazione, ci manca la misura del raggio.
Ora, il raggio della circonferenza ha misura uguale alla distanza tra il centro della circonferenza ed un qualsiasi punto della circonferenza stessa. Considerando ad esempio la distanza tra il punto {A} e il punto {M}, applicando la formula della distanza tra due punti si ha:
\begin{align*} &\overline{MA}=\sqrt{(x_M-x_A)^2+(y_M-y_A)^2}=\\ \\ & =\sqrt{\left( \dfrac{x_A+x_B}{2}-x_A\right)^2+\left( \dfrac{y_A+y_B}{2}-y_A\right)^2}=\\ \\ & =\sqrt{\left(\dfrac{x_A+x_B-2x_A}{2}\right)^2+\left( \dfrac{y_A+y_B-2y_A}{2}\right)^2}=\\ \\ & =\sqrt{\left(\dfrac{x_B-x_A}{2}\right)^2+\left( \dfrac{y_B-y_A}{2}\right)^2}=\\ \\ & =\sqrt{\dfrac{(x_B-x_A)^2}{4}+ \dfrac{\left( y_B-y_A\right)^2}{4}}=\\ \\ & =\sqrt{\dfrac{(x_B-x_A)^2+(y_B-y_A)^2}{4}}=r\end{align*}Ma a questo punto possiamo scrivere l’equazione della circonferenza nella forma con centro e raggio:
(x-x_C)^2+(y-y_C)^2=r^2
Abbiamo:
\begin{align*} &\left( x-\dfrac{x_A+x_B}{2}\right)^2+\left( y-\dfrac{y_A+y_B}{2}\right)^2=\left[ \sqrt{\dfrac{(x_B-x_A)^2+(y_B-y_A)^2}{4}}\right]^2\end{align*}Calcoliamo i quadrati dei binomi al primo membro e il quadrato al secondo membro:
\small \begin{align*} &x^2-(x_A+x_B)x+\dfrac{(x_A+x_B)^2}{4}+y^2-(y_A+y_B)y+\dfrac{(y_A+y_B)^2}{4}=\dfrac{(x_B-x_A)^2+(y_B-y_A)^2}{4}\end{align*}Proseguendo i calcoli:
\begin{align*} &4x^2-4(x_A+x_B)x+(x_A+x_B)^2+4y^2-4(y_A+y_B)y+\\ \\ & +(y_A+y_B)^2-(x_B-x_A)^2-(y_B-y_A)^2=0; \\ \\ & 4x^2-4x_Ax-4x_Bx+\cancel{x_A^2}+2x_Ax_B+\cancel{x_B^2}+4y^2-4y_Ay-4y_By+\\ \\ & +\cancel{y_A^2}+2y_Ay_B+\cancel{y_B^2}-\cancel{x_B^2}+2x_Ax_B-\cancel{x_A^2}-\cancel{y_B^2}+2y_Ay_B-\cancel{y_A^2}=0;\\ \\ &4x^2+4y^2+(-4x_A-4x_B)x+(-4y_A-4y_B)y+4x_Ax_B+4y_Ay_B=0;\\ \\ & \boxed{x^2+y^2+(-x_A-x_B)x+(-y_A-y_B)y+x_Ax_B+y_Ay_B=0} \end{align*}Abbiamo in questo modo ottenuto l’equazione cercata. Infatti, abbiamo l’equazione in forma canonica della circonferenza il cui diametro ha per estremi i punti {A} e {B}. L’utilità dell’equazione sta nel fatto che i suoi coefficienti sono direttamente espressi in funzione delle coordinate dei punti estremi del diametro.
L’equazione scritta si riconduce alla forma canonica {x^2+y^2+ax+by+c=0} poiché ponendo {a=-x_A-x_B, b=-y_A-y_B} e infine {c=x_Ax_B+y_Ay_B} ritroviamo un’equazione in tale forma.
Volendo collaudare l’equazione in forma generale appena ottenuta, proviamo a scrivere l’equazione della circonferenza avente per diametro i punti {A=(2,5)} e {B=(-3, -7)}.
Cominciamo utilizzando il metodo standard. Ricaviamo anzitutto il punto medio del segmento {\overline{AB}}: questo sarà il centro della circonferenza.
\begin{align*} &M=\left( \dfrac{x_A+x_B}{2}, \dfrac{y_A+y_B}{2}\right)=\left( \dfrac{2-3}{2}, \dfrac{5-7}{2}\right)=\left( -\dfrac{1}{2}, -1\right)=C\end{align*}Il raggio della circonferenza sarà la distanza tra il punto {M}, che coincide con il centro {C} della circonferenza, ed uno dei due estremi del diametro, ad esempio il punto {A}:
\begin{align*} &r=\sqrt{(x_A-x_M)^2+(y_A-y_M)^2}=\sqrt{\left( 2+\dfrac{1}{2}\right)^2+\left( 5+1\right)^2}=\\ \\ & =\sqrt{\left( \dfrac{5}{2}\right)^2+6^2}=\sqrt{\dfrac{25}{4}+36}=\sqrt{\dfrac{25+144}{4}}=\dfrac{\sqrt{169}}{2}=\dfrac{13}{2}\end{align*}A questo punto l’equazione nella forma con centro e raggio della circonferenza di estremi {A} e {B} è:
\begin{align*} &(x-x_C)^2+(y-y_C)^2=r^2 \quad \Rightarrow \quad \left( x+\dfrac{1}{2}\right)^2+(y+1)^2=\left( \dfrac{13}{2}\right)^2; \\ \\ &x^2+x+\dfrac{1}{4}+y^2+2y+1-\dfrac{169}{4}=0;\\ \\ & \boxed{x^2+y^2+x+2y-41=0}\end{align*}Questa è l’equazione in forma canonica della circonferenza il cui diametro ha estremi {A=(2,5)} e {B=(-3,-7)}.
Vediamo se utilizzando l’equazione in forma generale precedentemente ricavata otteniamo lo stesso risultato. Sostituiamo quindi nell’equazione:
x^2+y^2+(-x_A-x_B)x+(-y_A-y_B)y+x_Ax_B+y_Ay_B=0
le coordinate degli estremi del diametro, ovvero {x_A=2, y_A=5, x_B=-3, y_B=-7} (attenzione ai segni):
\begin{align*} &x^2+y^2+(-2+3)x+(-5+7)y+2 \cdot (-3)+5 \cdot (-7)=0; \\ \\ & \boxed{x^2+y^2+x+2y-41=0}\end{align*}Abbiamo correttamente ritrovato grazie alla formula che abbiamo elaborato l’equazione già ottenuta in precedenza con il metodo standard. Utilizzando l’equazione generale ricavata in questo esercizio la procedura è sicuramente più rapida, ma l’equazione non è così facile da ricordare. Utilizzeremo comunque la formula in uno degli ultimi esercizi di riepilogo sulla circonferenza di questa scheda.
Dopo questo esercizio di valenza teorica, torniamo ad esercizi di riepilogo sulla circonferenza di tipo più usuale.
Esercizio 3
Consideriamo la circonferenza di equazione:{x^2+y^2-8x-4y+10=0}Le tangenti alla circonferenza condotte dall’origine toccano la circonferenza stessa in due punti {A} e {B}. Trovare l’equazione della circonferenza passante per l’origine e per i due punti {A} e {B}.
Dopo i precedenti esercizi di riepilogo sulla circonferenza di “riscaldamento”, cominciamo con un esercizio che richiede l’utilizzo di diverse conoscenze tra quelle acquisite nell’ambito delle lezioni sulla circonferenza.
Dal testo sappiamo che esistono due rette tangenti alla circonferenza di equazione {x^2+y^2-8x-4y+10=0} e tali da passare per l’origine.
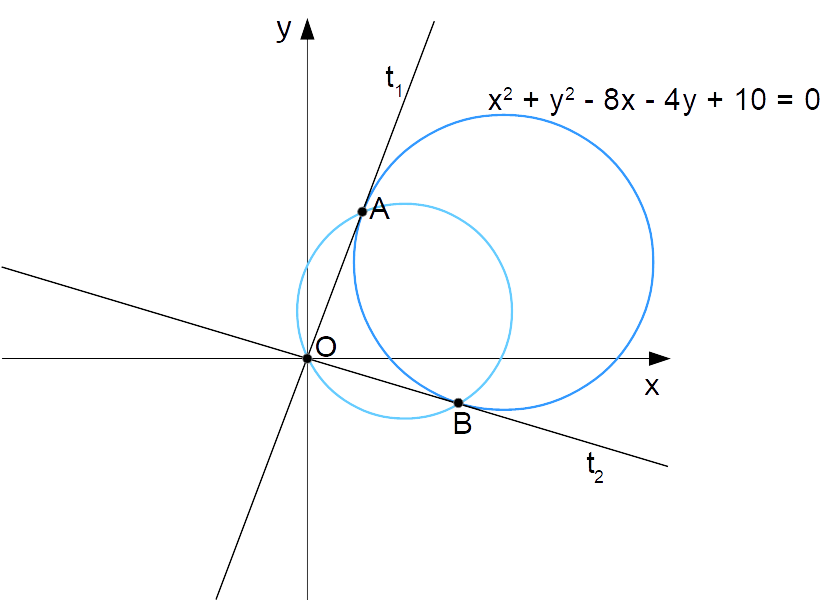
Sfruttando la formula della retta passante per un punto e con coefficiente angolare noto, l’equazione di ciascuna di tali rette può essere espressa in forma generale come:
y-0=m(x-0) \quad t: \Rightarrow y=mx
ove il coefficiente {m} è incognito.
Se la retta {t} è tangente alla circonferenza, il seguente sistema dovrà risultare determinato:
\begin{cases} x^2+y^2-8x-4y+10=0 \\ \\ y=mx\end{cases}Il sistema infatti consente di ricavare i punti di intersezione tra la circonferenza e la retta ad essa tangente {y=mx}.
Ora, se la retta {y=mx} è tangente alla circonferenza, l’equazione risolvente relativa al sistema scritto dovrà avere determinante nullo.
Sostituiamo l’espressione {mx} alla {y} nella prima equazione a sistema. In questo modo otteniamo l’equazione risolvente:
x^2+(mx)^2-8x-4mx+10=0
Svolgendo i calcoli:
\begin{align*} &x^2+m^2x^2-8x-4mx+10=0;\\ \\ & (1+m^2)x^2+(-8-4m)x+10=0\end{align*}Quella appena scritta è l’equazione risolvente del sistema. Si tratta di un’equazione di secondo grado con coefficienti dipendenti dal coefficiente angolare {m}, che in questo caso può essere visto a tutti gli effetti come un parametro.
Poiché sappiamo che la circonferenza ha due rette tangenti passanti per l’origine, imponiamo che il determinante di tale equazione sia nullo. Osserviamo che l’equazione è nella forma normale {ax^2+bx+c=0} con {a=1+m^2, b=-8-4m} e infine {c=10}. Di conseguenza, la condizione di determinante nullo:
b^2-4ac=0
ovvero utilizzando il Delta/4:
\left( \dfrac{b}{2}\right)^2-ac=0nel nostro caso diviene:
\begin{align*} &(-4-2m)^2-(1+m^2) \cdot 10=0; \\ \\ & 16+16m+4m^2-10-10m^2=0;\\ \\ & -6m^2+16m+6=0; \\ \\ & 6m^2-16m-6=0\end{align*}A questo punto abbiamo ottenuto un’equazione di secondo grado nella sola incognita {m}, che possiamo risolvere:
\begin{align*} &m_{1,2}=\dfrac{8 \pm \sqrt{(-8)^2-6 \cdot (-6)}}{6}=\dfrac{8 \pm \sqrt{100}}{6}=\dfrac{8\pm 10}{6}=\begin{cases} 3 \\ \\ -\dfrac{1}{3}\end{cases}\end{align*}Così le due rette tangenti alla circonferenza hanno coefficienti angolari {m_1=3} ed {m_2=-\dfrac{1}{3}}. Di conseguenza, poiché ciascuna tangente è esprimibile come {y=mx}, sostituendo i valori di {m} abbiamo le due seguenti equazioni delle rette tangenti alla circonferenza e passanti per l’origine:
t_1: y=3x; \qquad t_2: y=-\dfrac{1}{3}xTra parentesi osserviamo che, poiché un coefficiente angolare è l’inverso del reciproco dell’altro, le due rette sono perpendicolari tra loro.
Ma a questo punto possiamo ricavare i punti {A} e {B} come intersezioni tra la circonferenza data e ciascuna delle rette appena scritte. Abbiamo per la retta {t_1}:
\begin{cases} x^2+y^2-8x-4y+10=0 \quad \rightarrow \quad x^2+9x^2-8x-12x+10 = 0\\ \\ y=3x\end{cases}da cui:
\begin{cases} 10x^2-20x+10=0 \quad \rightarrow \quad x^2-2x+1=0 \quad \rightarrow \quad x_1 =1, \: x_2=1 \\ \\ y=3 \cdot 1 \quad \rightarrow \quad y=3\end{cases}Di conseguenza la tangente {t_1} tocca la circonferenza nel punto {A=(1,3)}.
Nota: osserviamo che dall’equazione di secondo grado a sistema otteniamo due valori reali e coincidenti per {x}, ma a lato pratico consideriamo un solo valore.
Allo stesso modo procediamo determinando le coordinate del punto {B}:
\begin{cases} x^2+y^2-8x-4y+10=0 \\ \\\ y=-\dfrac{1}{3}x\end{cases}Risolvendo il sistema abbiamo:
\begin{cases} x^2+\left( -\dfrac{1}{3}x\right)^2-8x+\dfrac{4}{3}x+10=0 \quad \rightarrow \quad x^2+\dfrac{1}{9}x^2-8x+\dfrac{4}{3}x+10=0 \\ \\ y=-\dfrac{1}{3}x\end{cases}da cui:
\begin{cases} \dfrac{10}{9}x^2-\dfrac{20}{3}x+10=0 \quad \rightarrow \quad 10x^2-60x+90=0 \quad \rightarrow \quad x^2-6x+9=0\\ \\ y=-\dfrac{1}{3}x\end{cases}e quindi:
\begin{cases} x^2-6x+9=0 \quad \rightarrow \quad x_{1}=3, \quad x_2=3 \\ \\ y=-\dfrac{1}{3} \cdot 3 \quad \rightarrow \quad y=-1\end{cases}Quindi il punto {B} è dato da {B=(3,-1)}.
A questo punto possiamo scrivere l’equazione della circonferenza passante per l’origine e per i punti {A} e {B}, come richiesto dal testo. Allo scopo ricordiamo quanto visto nella lezione sulle condizioni per determinare l’equazione di una circonferenza, con riferimento al caso dei tre punti non allineati.
Utilizziamo il metodo basato sulle condizioni di appartenenza di ciascun punto alla circonferenza. Indicando le coordinate di ciascun punto con:
A=(1,3)=(x_A, y_A); \qquad B=(3,-1)=(x_B, y_B); \quad O=(x_O, y_O)
abbiamo:
\begin{cases} x_A^2+y_A^2+ax_A+bx_A+c=0 \\ \\ x_B^2+y_B^2+ax_B+bx_B+c=0 \\ \\ x_O^2+y_O^2+ax_O+by_O+c=0\end{cases}Ricordiamo che l’idea è quella di imporre contemporaneamente le condizioni di appartenenza di ciascun punto alla circonferenza. L’obiettivo è ricavare i coefficienti {a,b,c} che permettono di scrivere l’equazione in forma canonica della circonferenza passante per i tre punti {A, B, O}. Sostituendo le coordinate dei punti assegnati nel precedente sistema otteniamo:
\begin{cases}1^2+3^2+a\cdot1+3b+c=0 \\ \\ 3^2+(-1)^2+3a-1 \cdot b + c= 0 \\ \\ 0^2+0^2+a \cdot 0 + b \cdot 0 +c = 0 \end{cases}ovvero:
\begin{cases} a+3b+c=-10 \\ \\ 3a-b+c=-10 \\ \\ c=0\end{cases}La terza equazione già ci fornisce il valore di {c}. Per cui conviene risolvere il sistema per sostituzione, ad esempio procedendo a ritroso (dall’ultima equazione in su fino alla prima):
\small \begin{cases} a+3b=-10 \quad \rightarrow a+3 \cdot (3a+10)=-10 \quad \rightarrow \: a+9a+30=-10 \quad \rightarrow \: a=-4 \\ \\ 3a-b=-10 \quad \rightarrow \quad b=3a+10\\ \\ c=0\end{cases}Infine sostituendo nella seconda equazione:
\begin{cases} a=-4 \\ \\ b=3 \cdot (-4)+10 \quad \rightarrow \: b =-2\\ \\ c=0\end{cases}Abbiamo ottenuto per i coefficienti dell’equazione in forma canonica della circonferenza cercata i valori:
a=-4, \quad b=-2, \quad c=0
per cui la circonferenza passante per i punti {A} e {B} e per l’origine ha equazione:
x^2+y^2-4x-2y=0
ed abbiamo concluso anche il terzo di questa serie di esercizi di riepilogo sulla circonferenza.
Esercizio 4
Determinare l’equazione della circonferenza passante per i punti {P_1=(2,4), P_2=(3,5)} e {P_3=(-2,9)}.
Cominciamo con lo scrivere l’equazione della circonferenza passante per i tre punti dati. Piuttosto che utilizzare le condizioni di appartenenza dei punti alla circonferenza come fatto nell’esercizio precedente, vediamo di avvalerci del metodo basato sulla ricerca del centro e del raggio. Riteniamo infatti importante per questi esercizi di riepilogo sulla circonferenza rivedere un po’ tutti i metodi esposti nelle lezioni. E l’utilizzo di tale metodo fornisce un’ottima occasione di ripasso.
Ricordiamo che il centro di una circonferenza si ottiene dall’intersezione degli assi dei segmenti aventi per estremi dei punti distinti appartenenti alla circonferenza. Così, dato che disponiamo delle coordinate di tre punti, l’idea è quella di costruire due segmenti ciascuno avente per estremi una distinta coppia di tali punti, e quindi ricercare il punto di intersezione fra gli assi di tali segmenti. Il punto che così troveremo sarà il centro della circonferenza. Successivamente basterà ricavare il raggio della circonferenza come distanza fra il centro e uno dei tre punti dati inizialmente. Infine, sarà possibile scrivere l’equazione con centro e raggio ed eventualmente l’equazione in forma canonica della circonferenza cercata.
Scegliamo di considerare i segmenti {\overline{P_1P_2}} e {\overline{P_2P_3}}.
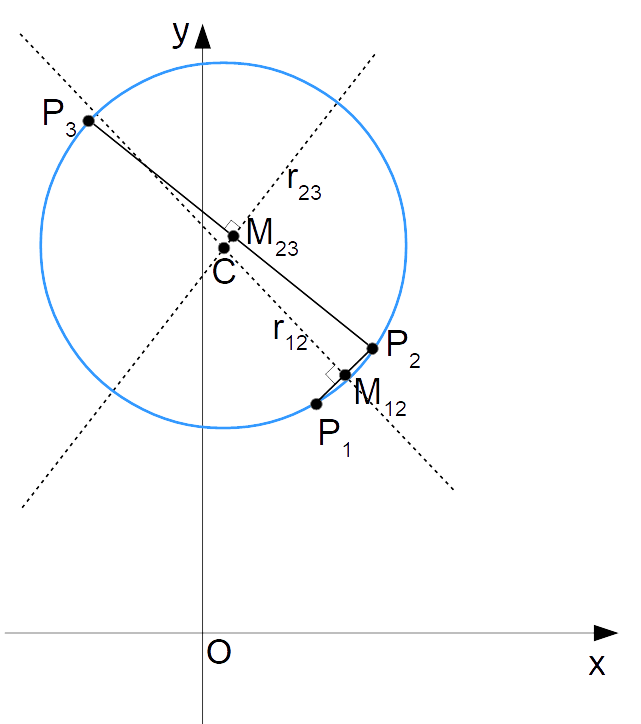
Cominciamo calcolando i punti medi dei segmenti ed i coefficienti angolari delle rette passanti per i punti {P_1, P_2} e {P_2, P_3}. Tali coefficienti angolari ci serviranno per determinare i coefficienti angolari degli assi dei segmenti. Ricordiamo infatti che l’asse di un segmento è una retta perpendicolare al segmento e tale da passare per il suo punto medio.
Per i punti medi abbiamo, rispettivamente, per il segmento {\overline{P_1P_2}}:
\begin{align*} &M_{12}=\left( \dfrac{x_{P_1}+x_{P_2}}{2}, \dfrac{y_{P_1}+y_{P_2}}{2}\right)=\left( \dfrac{2+3}{2}, \dfrac{4+5}{2}\right)=\left( \dfrac{5}{2}, \dfrac{9}{2}\right)\end{align*}Per il segmento {\overline{P_2P_3}}:
M_{23}=\left( \dfrac{x_{P_2}+x_{P_3}}{2}, \dfrac{y_{P_2}+y_{P_3}}{2}\right)=\left( \dfrac{3-2}{2}, \dfrac{5+9}{2}\right)=\left( \dfrac{1}{2}, 7\right)Veniamo ora ai coefficienti angolari. Per il coefficiente angolare della retta passante per i punti {P_1, P_2} si ha:
m_{12}=\dfrac{y_{P_2}-y_{P_1}}{x_{P_2}-x_{P_1}}=\dfrac{5-4}{3-2}=1E per il coefficiente angolare della retta passante per i punti {P_2, P_3}:
m_{23}=\dfrac{y_{P_3}-y_{P_2}}{x_{P_3}-x_{P_2}}=\dfrac{9-5}{-2-3}=\dfrac{4}{-5}=-\dfrac{4}{5}Ricordiamo a questo punto l’equazione di una retta passante per un punto con coefficiente angolare noto (una formula piuttosto ricorrente in questa serie di esercizi di riepilogo sulla circonferenza):
y-y_0=m(x-x_0)
Nel nostro caso, l’asse del segmento {\overline{P_1P_2}}, che indicheremo con {r_{12}}, passa per il punto medio {M_{12}} ed ha coefficiente angolare {-\dfrac{1}{m_{12}}}, ovvero l’inverso del reciproco del coefficiente angolare della retta passante per i punti {P_1} e {P_2}. Ciò si giustifica tenendo conto del fatto che l’asse di un segmento è perpendicolare al segmento stesso, e ricordando la relazione di perpendicolarità fra rette.
r_{12}:y-y_{M_{12}}=-\dfrac{1}{m_{12}} (x-x_{M_{12}}) \quad \Rightarrow \quad y-\dfrac{9}{2}=-1 \cdot \left(x-\dfrac{5}{2}\right)da cui:
\begin{align*} &y=-x+\dfrac{5}{2}+\dfrac{9}{2} \quad \Rightarrow \quad r_{12}:y=-x+7\end{align*}Veniamo ora all’asse del segmento {\overline{P_2P_3}}. In modo del tutto simile abbiamo:
r_{23}: y-y_{M_{23}}=-\dfrac{1}{m_{23}} (x-x_{M_{23}})ovvero:
\begin{align*} &y-7=\dfrac{5}{4}\left(x-\dfrac{1}{2}\right); \\ \\ &y=\dfrac{5}{4}x-\dfrac{5}{8}+7; \\ \\ &r_{23}: y=\dfrac{5}{4}x+\dfrac{51}{8}\end{align*}A questo punto disponiamo delle equazioni degli assi dei segmenti e possiamo procedere alla ricerca del loro punto di intersezione, le cui coordinate corrisponderanno a quelle del centro della circonferenza. Impostiamo il sistema per la determinazione dei punti di intersezione tra le due rette:
\begin{cases} r_{12}: y=-x+7 \\ \\ r_{23}: y=\dfrac{5}{4}x+\dfrac{51}{8}\end{cases}Risolviamo il sistema utilizzando il metodo del confronto. Ciò riesce comodo poiché entrambe le equazioni delle rette sono espresse in forma esplicita.
\small \begin{cases} y=-x+7 \\ \\ -x+7=\dfrac{5}{4}x+\dfrac{51}{8} \quad \rightarrow \quad \dfrac{5}{4}x+x=7-\dfrac{51}{8} \quad \rightarrow \quad x=\dfrac{4}{9}\cdot \dfrac{5}{8} \quad \rightarrow \: x =\dfrac{5}{18}\end{cases}Sostituendo il valore appena ottenuto per la {x} nella prima equazione:
\begin{cases} y=-\dfrac{5}{18}+7 \quad \rightarrow \quad y=\dfrac{121}{18} \\ \\ x=\dfrac{5}{18}\end{cases}Così il punto di intersezione fra le due rette, ovvero il centro della circonferenza dato dall’intersezione degli assi dei due segmenti precedentemente costruiti, è:
C=\left( \dfrac{5}{18}, \dfrac{121}{18}\right)Ora determiniamo il raggio della circonferenza come distanza tra il centro {C} e ad esempio il punto {P_1=(2,4)}:
\begin{align*} & r=\overline{CP_1}=\sqrt{(x_{P_1}-x_C)^2+(y_{P_1}-y_C)^2}=\sqrt{\left(2-\dfrac{5}{18}\right)^2+\left( 4-\dfrac{121}{18}\right)^2}= \\ \\ & =\sqrt{\dfrac{961}{324}+\dfrac{2401}{324}}=\sqrt{\dfrac{3362}{324}}=\sqrt{\dfrac{1681}{162}}\end{align*}Disponiamo a questo punto delle coordinate del centro e della misura del raggio della circonferenza. Possiamo quindi scrivere in conclusione la sua equazione con centro e raggio:
(x-x_C)^2+(y-y_C)^2=r^2
ovvero sostituendo i valori:
\left( x-\dfrac{5}{18}\right)^2+\left( y-\dfrac{121}{18}\right)^2=\dfrac{1681}{162}Esercizio 5
Scrivere l’equazione della retta {t} tangente alla circonferenza di equazione {x^2+y^2-4x-14y+28=0} nel punto {P=(-3, 7)} appartenente alla circonferenza stessa. Determinare inoltre le equazioni delle rette tangenti alla circonferenza condotte per il punto esterno {Q=\left( \dfrac{2}{5}, \dfrac{4}{5}\right)}.
Rivediamo come scrivere l’equazione della retta tangente ad una circonferenza in un punto appartenente alla circonferenza stessa. Possiamo utilizzare due metodi, che riepiloghiamo brevemente a seguire. I richiami seguenti si riveleranno utili anche per i successivi esercizi di riepilogo sulla circonferenza.
Relazione di perpendicolarità fra rette. La retta che passa per il centro della circonferenza e per il punto {P} di tangenza è perpendicolare alla retta tangente. Di conseguenza, una volta noto il coefficiente angolare della retta passante per il centro {C} della circonferenza e per il punto {P}, sarà possibile scrivere l’equazione della tangente. Infatti, quest’ultima essendo perpendicolare alla retta per {C} e per {P} avrà coefficiente angolare uguale all’inverso del reciproco di quello relativo alla retta per {C} e per {P}. Inoltre, la retta tangente passa necessariamente per il punto di tangenza, fatto grazie al quale è possibile scrivere la sua equazione mediante la formula della retta passante per un punto e con coefficiente angolare noto. Osserviamo che nei casi in cui la retta per {C} e {P} sia orizzontale o verticale il metodo è comunque applicabile, e basterà osservare che una retta perpendicolare ad una retta orizzontale è verticale e viceversa.

Formule di sdoppiamento. Le formule di sdoppiamento consentono, mediante delle semplici sostituzioni, di ricavare, a partire dall’equazione in forma canonica della circonferenza, l’equazione della retta tangente alla circonferenza in un punto appartenente alla circonferenza stessa.
Il primo metodo è più ragionato ma non richiede di dover ricordare della formule specifiche. Il secondo metodo è più meccanico e quindi più diretto ma richiede di ricordare le formule di sdoppiamento della circonferenza. A seguire proponiamo l’applicazione di entrambi i metodi.
Relazione di perpendicolarità fra rette. Calcoliamo il coefficiente angolare della retta passante per i punti {C} e {P}. Se non si ricorda la formula del coefficiente angolare, è comunque possibile determinare l’equazione di tale retta in forma esplicita. A tal punto, il coefficiente angolare è ricavabile in modo immediato.
In ogni caso, abbiamo prima di tutto bisogno delle coordinate del centro {C} della circonferenza. Queste si ricavano a partire dall’equazione in forma canonica della circonferenza {x^2+y^2+ax+by+c=0} mediante le formule:
x_C=-\dfrac{1}{2}a, \quad y_C=-\dfrac{1}{2}bovvero nel nostro caso:
x_C=-\dfrac{1}{2} \cdot (-4)=2; \qquad y_C=-\dfrac{1}{2} \cdot (-14)=7Proseguiamo calcolando direttamente il coefficiente angolare {m_{CP}} della retta passante per {C} e per {P}. Si ha:
m_{CP}=\dfrac{y_P-y_C}{x_P-x_C}=\dfrac{7-7}{-3-2}=\dfrac{0}{-5}=0Il coefficiente angolare è nullo ed a ciò corrisponde una retta orizzontale. Di conseguenza, la retta tangente alla circonferenza nel punto {P} sarà verticale (perpendicolare alla retta passante per {C} e {P}). Inoltre, dovendo questa passare per il punto di tangenza {P=(-3,7)} dovrà necessariamente avere equazione:
t: x=-3
Infatti questa è l’unica retta verticale tale da passare per {P} (il secondo membro dell’equazione presenta il valore dell’ascissa del punto di tangenza {P}).
Formule di sdoppiamento. Data l’equazione in forma canonica di una circonferenza (reale e non degenere):
x^2+y^2+ax+by+c=0
indicato con {P=(x_P, y_P)} il punto della circonferenza in cui una retta {t} è tangente alla circonferenza stessa, valgono le seguenti formule di sdoppiamento:
x^2 \rightarrow x_P \cdot x; \qquad y^2\rightarrow y_P\cdot y; \qquad x\rightarrow \dfrac{x+x_P}{2}; \qquad y\rightarrow \dfrac{y+y_P}{2}Grazie a tali formule è possibile mediante le corrispondenti sostituzioni ricondurre l’equazione della circonferenza all’equazione della tangente alla circonferenza stessa nel suo punto {P}. Nel nostro caso le formule di trasformazione divengono, sostituendo i valori delle coordinate del punto {P}:
x^2\rightarrow -3x; \qquad y^2\rightarrow 7y; \qquad x\rightarrow \dfrac{x-3}{2}; \qquad y\rightarrow \dfrac{y+7}{2}Sostituiamo a questo punto, nell’equazione in forma canonica della circonferenza, ad {x^2} l’espressione {-3x}, ad {y^2} l’espressione {7y} e così via. Abbiamo:
\begin{align*} &x^2+y^2-4x-14y+28=0 \\ \\ & \Rightarrow -3x+7y-4\left( \dfrac{x-3}{2}\right)-14\left( \dfrac{y+7}{2}\right)+28=0; \\ \\ &-3x+\cancel{7y}-2x+6-\cancel{7y}-49+28=0;\\ \\ & -5x-15=0; \\ \\ & t:x=-3 \end{align*}Ritroviamo così, correttamente, lo stesso risultato per la retta tangente alla circonferenza nel punto {P} ad essa appartenente.
Vale decisamente la pena ricordare le formule di sdoppiamento, poiché specialmente nel caso degli esercizi di riepilogo sulla circonferenza, essendo presenti vari quesiti, consentono di risparmiare molto tempo.
Ricerchiamo ora la rette tangenti alla circonferenza tali da passare per il punto esterno alla circonferenza:
Q=\left( \dfrac{2}{5}, \dfrac{4}{5}\right)Per fare questo esistono due metodi:
- scrivere il sistema relativo ai punti di intersezione tra la circonferenza e una generica retta tangente passante per {Q}, e quindi ricavare i valori dei coefficienti angolari delle due rette tangenti imponendo uguale a zero il determinante dell’equazione risolvente del sistema;
- utilizzare la formula per la distanza di una retta da un punto, tenendo conto che la distanza tra una retta tangente alla circonferenza e il centro della circonferenza stessa è necessariamente uguale al raggio. In tal modo, ricaveremo i valori dei coefficienti angolari corrispondenti alle rette che soddisfano tale condizione.
Il primo metodo è quello più semplice come ragionamento da adottare, ma richiede dei calcoli un po’ più pesanti. Il secondo metodo richiede un po’ più di ragionamento ma alleggerisce i calcoli necessari. Abbiamo visto entrambi i metodi in azione nella lezione: rette tangenti ad una circonferenza passanti per un punto esterno.
Scegliamo qui di utilizzare il primo metodo, sperando di non imbatterci in calcoli troppo lunghi. In generale, comunque, specialmente nell’ambito di lunghi esercizi di riepilogo (quali gli esercizi di riepilogo qui proposti sulla circonferenza), è sempre bene scegliere il metodo più breve.
Possiamo scrivere l’equazione della generica retta tangente alla circonferenza data e passante per il punto esterno {Q} come:
s: y-y_Q=m_S(x-x_Q)
ovvero, dato che le coordinate del punto {Q} sono note:
s:y-\dfrac{4}{5}=m_s \left( x-\dfrac{2}{5}\right)ovvero in forma esplicita:
s:y=m_sx-\dfrac{2}{5}m_s+\dfrac{4}{5}Il sistema che permette di individuare i punti di intersezione tra la circonferenza data e la retta {s} è:
\begin{cases} x^2+y^2-4x-14y+28=0 \\ \\ y=m_sx-\dfrac{2}{5}m_s+\dfrac{4}{5}\end{cases}Sostituendo l’espressione per {y} che fornisce la seconda equazione nella prima equazione abbiamo, considerando separatamente quest’ultima:
\small \begin{align*} &x^2+\left( m_sx-\dfrac{2}{5}m_s+\dfrac{4}{5}\right)^2-4x-14\left( m_sx-\dfrac{2}{5}m_s+\dfrac{4}{5} \right)+28=0;\\ \\ & x^2+m_s^2x^2+\dfrac{4}{25}m_s^2+\dfrac{16}{25}-\dfrac{4}{5}m_s^2x+\dfrac{8}5{m_sx-\dfrac{16}{25}m_s-4x-14m_sx+\dfrac{28}{5}m_S-\dfrac{56}{5}+28=0;} \end{align*}Prima di tutto abbiamo calcolato i prodotti al primo membro, sviluppando tra l’altro il quadrato di un trinomio.
Proseguiamo raccogliendo per {x^2, x} e i termini noti:
\small \begin{align*} & (1+m_s^2)x^2+\left(-\dfrac{4}{5}m_s^2+\dfrac{8}{5}m_s-4-14m_s\right)x+\dfrac{4}{25}m_s^2+\dfrac{16}{25}-\dfrac{16}{25}m_s+\dfrac{28}{5}m_s-\dfrac{56}{5}+28=0; \\ \\ &\boxed{ (1+m_s^2)x^2+\left(-\dfrac{4}{5}m_s^2-\dfrac{62}{5}m_s-4\right)x+\dfrac{4}{25}m_s^2 +\dfrac{124}{25}m_s+\dfrac{436}{25}=0}\end{align*}Abbiamo così ottenuto l’equazione risolvente del sistema. Ora, il nostro obiettivo è ricercare quei valori del coefficiente angolare {m_s} che corrispondono alle due rette tangenti {s_1} ed {s_2} alla circonferenza per il punto esterno {Q}. Si tratta allora di imporre il determinante dell’equazione risolvente uguale a zero. Osserviamo che i coefficienti dell’equazione dipendono da {m_s}, per cui imponendo tale condizione ci ritroviamo con un’equazione nella sola incognita {m_s}:
\begin{align*} &\left(-\dfrac{4}{5}m_s^2-\dfrac{62}{5}m_s-4\right)^2-4 \cdot (1+m_s^2) \cdot \left( \dfrac{4}{25}m_s^2 +\dfrac{124}{25}m_s+\dfrac{436}{25}\right)=0\end{align*}Sviluppiamo i calcoli fino ad ottenere un’equazione di secondo grado in forma normale nell’incognita {m_s} (occorre aiutarsi con una calcolatrice visti i numeri un po’ ingombranti):
\begin{align*} &\dfrac{16}{25}m_s^4+\dfrac{3844}{25}m_s^2+16+\dfrac{62\cdot8}{25}m_s^3+\dfrac{32}{5}m_s^2+\dfrac{62 \cdot 8}{5}m_s+ \\ \\ & -4 \cdot \left(\dfrac{4}{25}m_s^2 +\dfrac{124}{25}m_s+\dfrac{436}{25}+\dfrac{4}{25}m_s^4+\dfrac{124}{25}m_s^3+\dfrac{436}{25}m_s^2\right)=0;\\ \\ & \cancel{\dfrac{16}{25}m_s^4}+\dfrac{3844}{25}m_s^2+16+\cancel{\dfrac{496}{25}m_s^3}+\dfrac{32}{5}m_s^2+\dfrac{496}{5}m_s-\dfrac{16}{25}m_s^2-\dfrac{496}{25}m_s+\\ \\ & -\dfrac{1744}{25}-\cancel{\dfrac{16}{25}m_s^4}-\cancel{\dfrac{496}{25}m_s^3}-\dfrac{1744}{25}m_s^2=0;\\ \\ & \left( \dfrac{3844}{25}+\dfrac{32}{5}-\dfrac{16}{25}-\dfrac{1744}{25}\right)m_s^2+\left( \dfrac{496}{5}-\dfrac{496}{25}\right)m_s+16-\dfrac{1744}{25}=0;\\ \\ &\dfrac{2244}{25}m_s^2+\dfrac{1984}{25}m_s-\dfrac{1344}{25}=0; \\ \\ &561m_s^2+496m_s-336=0 \end{align*}Ora non resta che risolvere l’equazione di secondo grado (formula ridotta):
\begin{align*} &m_{s_{1,2}}=\dfrac{-248\pm \sqrt{\left(248\right)^2-561 \cdot (-336)}}{561}=\dfrac{-248\pm \sqrt{61504+188496}}{561}=\\ \\ & =\dfrac{-248\pm \sqrt{250000}}{561}=\dfrac{-248\pm 500}{561}=\begin{cases} \dfrac{252}{561}=\dfrac{84}{187} \\ \\ -\dfrac{748}{561}=-\dfrac{4}{3}\end{cases}\end{align*}Abbiamo così per le rette tangenti alla circonferenza condotte per il punto esterno {Q} i coefficienti angolari {m_{s_1}=\dfrac{84}{187}} e {m_{s_2}=-\dfrac{4}{3}}. Di conseguenza, sostituendo tali valori nell’equazione precedentemente scritta:
s:y=m_sx-\dfrac{2}{5}m_s+\dfrac{4}{5}otteniamo in conclusione le equazioni delle rette tangenti cercate:
s_1:y=\dfrac{84}{187}x+\dfrac{116}{187}; \qquad s_2:y=-\dfrac{4}{3}x+\dfrac{4}{3}Proseguiamo ancora gli esercizi di riepilogo sulla circonferenza con il seguente, che costituisce un’applicazione di quanto visto sulle condizioni per determinare l’equazione di una circonferenza.
Esercizio 6
Determinare l’equazione della circonferenza passante per i punti {A=(-2, 0)} e {B=(6,0)}, ed il cui centro appartiene alla retta {x+2y+4=0}. Determinare inoltre le equazioni delle tangenti alla circonferenza passanti per il punto esterno {P=(-5,2)}.
Per scrivere l’equazione della circonferenza dobbiamo ricordare quanto visto nella lezione sulle condizioni per determinare l’equazione di una circonferenza (lezione molto importante per questa serie di esercizi di riepilogo sulla circonferenza). In particolare, siamo nel caso in cui sono noti due punti della circonferenza e l’equazione di una retta passante per il centro della circonferenza stessa.
Il primo passo consiste nel determinare le coordinate del punto medio {M_{AB}} del segmento avente per estremi i punti {A} e {B}. Per tale punto passa infatti l’asse del segmento {\overline{AB}}, la cui equazione ci servirà per determinare il centro della circonferenza.
M_{AB}=\left( \dfrac{x_A+x_B}{2}, \dfrac{y_A+y_B}{2}\right)=\left( \dfrac{-2+6}{2}, 0\right)=(2,0)Ora determiniamo il coefficiente angolare della retta passante per {A} e {B}:
m_{AB}=\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{0-0}{6+2}=0Così la retta passante per {A} e {B} è orizzontale. L’asse del segmento {\overline{AB}} dovrà essere perpendicolare a tale retta e quindi verticale. L’asse del segmento avrà quindi equazione del tipo {x=c}, con {c} numero reale. Inoltre, tale asse deve anche passare per il punto medio {M_{AB}}. Ma avendo tale punto ordinata {2}, l’equazione dell’asse del segmento dovrà essere necessariamente:
r_{AB}: x=2Ora, il centro della circonferenza appartiene ad {r_{AB}}. Infatti, per la geometria elementare l’asse di un qualunque segmento avente per estremi due distinti punti di una circonferenza passa per il centro della circonferenza stessa. Ma dato che come dice il testo anche la retta {x+2y+4=0} passa per il centro della circonferenza, le coordinate del centro saranno date dall’intersezione dell’asse {r_{AB}} e di tale retta:
\begin{cases} x=2 \\ \\ x+2y+4=0\end{cases}Risolvendo il sistema per sostituzione abbiamo:
\begin{cases} x=2 \\ \\ 2+2y+4=0 \quad \rightarrow \quad y=\dfrac{-4-2}{2}=-3\end{cases}Di conseguenza il centro della circonferenza {C} è:
C=(2,-3)

Ora per scrivere l’equazione della circonferenza ci manca soltanto il raggio. Ma questo può essere calcolato come la distanza ad esempio tra il centro {C} e il punto {B}:
r=\sqrt{(x_B-x_C)^2+(y_B-y_C)^2}=\sqrt{(6-2)^2+(0+3)^2}=\sqrt{16+9}=\sqrt{25}=5Disponiamo così di tutti gli ingredienti per poter scrivere l’equazione della circonferenza nella forma con centro e raggio:
(x-x_C)^2+(y-y_C)^2=r^2 \quad \Rightarrow \quad (x-2)^2+(y+3)^2=5^2
e quindi:
(x-2)^2+(y+3)^2=25
Ora, riconduciamo l’equazione appena scritta alla forma canonica. Per fare questo, possiamo calcolare i coefficienti {a,b,c} con le formule dedicate oppure sviluppare i quadrati. Scegliamo la seconda strada:
\begin{align*} & x^2-4x+4+y^2+6y+9-25=0; \\ \\ & \boxed{x^2+y^2-4x+6y-12=0} \end{align*}Vediamo ora come determinare le equazioni delle rette tangenti alla circonferenza condotte per il punto esterno {P=(-5,2)} alla circonferenza avente l’equazione appena scritta.
Cominciamo scrivendo l’equazione di una generica retta tangente passante per {P}:
t:y-y_P=m_t (x-x_P)
ove {m_t} è da determinare. Sostituendo intanto i valori delle coordinate del punto {P} abbiamo:
t:y-2=m_t(x+5)
ovvero in forma esplicita:
t:y=m_tx+5m_t+2
Ora, impostiamo il sistema relativo all’intersezione tra la circonferenza di equazione {x^2+y^2-4x+6y-12=0} e la generica retta tangente passante per {P}:
\begin{cases} x^2+y^2-4x+6y-12=0 \\ \\ y=m_tx+5m_t+2\end{cases}Sostituiamo l’espressione corrispondente a {y} fornita dalla seconda equazione nella prima equazione a sistema:
\begin{align*} &x^2+(m_tx+5m_t+2)^2-4x+6m_tx+30m_t+\cancel{12}-\cancel{12}=0;\\ \\ & x^2+m_t^2x^2+25m_t^2+4+10m_t^2x+4m_tx+20m_t-4x+6m_tx+30m_t=0;\\ \\ & (1+m_t^2)x^2+(10m_t^2+4m_t-4+6m_t)x+25m_t^2+4+20m_t+30m_t=0;\\ \\ & (1+m_t^2)x^2+(10m_t^2+10m_t-4)x+25m_t^2+50m_t+4=0;\end{align*}Abbiamo così ottenuto l’equazione risolvente del sistema, i cui coefficienti dipendono dal coefficiente angolare {m_t}.
Ora, poiché ricerchiamo le rette tangenti alla circonferenza, dobbiamo richiedere che il determinante dell’equazione risolvente sia nullo e risolvere rispetto ad {m_t} l’equazione corrispondente. In tal modo determineremo i coefficienti angolari delle rette tangenti alla circonferenza e passanti per {P}.
\small\begin{align*} &\left( \dfrac{b}{2}\right)^2-ac=0;\\ \\ & (5m_t^2+5m_t-2)^2-(1+m_t^2) \cdot (25m_t^2+50m_t+4)=0;\\ \\ & \cancel{25m_t^4}+\cancel{25m_t^2}+\cancel{4}+\cancel{50m_t^3}-20m_t^2-20m_t-\cancel{25m_t^2}-50m_t-\cancel{4}-\cancel{25m_t^4}-\cancel{50m_t^3}-4m_t^2=0;\\ \\ &-24m_t^2-70m_t=0;\\ \\ & 12m_t^2+35m_t=0 \quad \Rightarrow \quad m_t(12m_t+35)=0 \quad \Rightarrow \quad m_t=0 \quad \vee \quad m_t=-\dfrac{35}{12} \end{align*}Abbiamo così ottenuto i valori dei coefficienti angolari corrispondenti alla rette tangenti alla circonferenza e passanti per il punto {P}. Sostituendo in particolare i valori appena ottenuti nell’equazione in forma generica:
t:y=m_tx+5m_t+2
otteniamo in conclusione:
t_1: y=2; \qquad t_2:y=-\dfrac{35}{12}x-\dfrac{151}{12}Metodo della distanza punto-retta. In alternativa, per determinare le equazioni delle tangenti {t_1} e {t_2} passanti per il punto {P=(-5,2)}, avremmo anche potuto utilizzare il metodo basato sulla distanza punto-retta.
Tale metodo si basa sul fatto che la distanza tra una retta tangente ad una circonferenza e il centro della circonferenza stessa è uguale al raggio. Nel nostro caso, come visto nei passaggi precedenti sappiamo che il centro della circonferenza è {C=(2,-3)} e il raggio è {5}.
Ora, riprendiamo l’equazione della generica retta tangente alla circonferenza e passante per {P}:
t:y-2=m_t(x+5)
ovvero in forma implicita:
t: m_tx-y+5m_t+2=0
L’equazione è in questo modo della forma {ax+by+c=0} con {a=m_t, b=-1} e {c=5m_t+2}.
Ciò che dobbiamo fare è imporre che la distanza fra tale retta tangente e il centro della circonferenza sia uguale al raggio {r}, ovvero {5} (vedi: distanza di una retta da un punto nel piano).
\begin{align*} &d(t,C)=r \iff \dfrac{|ax_C+by_C+c|}{\sqrt{a^2+b^2}}=r\end{align*}Sostituendo i valori delle coordinate del centro {C} e le espressioni dei coefficienti {a,b,c} relativi all’equazione della retta {t} in forma implicita abbiamo:
\begin{align*} &\dfrac{|m_t \cdot 2+(-1)\cdot (-3)+5m_t+2| }{\sqrt{m_t^2+(-1)^2}}=5\end{align*}Il primo passo per risolvere l’equazione consiste nel portare tutti i termini al primo membro e metterli a denominatore comune:
\begin{align*} & \dfrac{|2m_t+3+5m_t+2|}{\sqrt{m_t^2+1}}=5; \\ \\ & \dfrac{|7m_t+5|}{\sqrt{m_t^2+1}}=5;\\ \\ & \dfrac{|7m_t+5|}{\sqrt{m_t^2+1}}-5=0;\\ \\ & \dfrac{|7m_t+5|-5\sqrt{m_t^2+1}}{\sqrt{m_t^2+1}}=0\\ \\ \end{align*}A questo punto è importante osservare che possiamo eliminare il denominatore senza alcuna discussione. Infatti, il radicando è una somma di quadrati e quindi sempre positivo. Il denominatore di conseguenza sarà diverso da zero per ogni valore di {m_t}. Proseguendo allora i passaggi:
|7m_t+5|=5\sqrt{m_t^2+1}Abbiamo ricondotto l’equazione all’uguaglianza tra una quantità in valore assoluto e un radicale con indice pari (moltiplicato per un numero positivo). In particolare, si tratta di un’equazione irrazionale.
Vediamo nel dettaglio come risolvere un’equazione della forma appena scritta, poiché molto ricorrente negli esercizi di riepilogo sulla circonferenza.
Ora, per risolvere l’equazione basta elevare al quadrato entrambi i membri, senza dovere in questo caso fare alcuna discussione. Infatti, non serve alcuna condizione di concordanza dei segni, poiché entrambi i membri sono sempre positivi. Inoltre, non serve nemmeno alcuna condizione di realtà, poiché come detto il radicando del radicale al secondo membro è sempre positivo.
Così abbiamo:
\begin{align*} &(7m_t+5)^2=25(m_t^2+1)\end{align*}Per il calcolo del quadrato al secondo membro è bastato ricordare che il quadrato di un prodotto è uguale al prodotto dei quadrati (proprietà delle potenze).
A questo punto è possibile ricondursi ad un’equazione di secondo grado, che risolta fornisce i valori per il coefficiente angolare {m_t}:
\begin{align*} &49m_t^2+70m_t+\cancel{25}-25m_t^2-\cancel{25}=0;\\ \\ & 24m_t^2+70m_t=0;\\ \\ & 12m_t^2+35m_t=0 \quad \Rightarrow \quad m_t=0 \quad \vee \quad m_t=-\dfrac{35}{12}\end{align*}Abbiamo ritrovato correttamente gli stessi valori dei coefficienti angolari delle rette tangenti cercate, ai quali corrispondono le rispettive equazioni già precedentemente scritte.
Come è evidente, il metodo della distanza punto-retta (per la ricerca delle rette tangenti ad una circonferenza condotte per un punto esterno) consente di alleggerire sensibilmente i calcoli da eseguire. Tuttavia, abbiamo l’onere di dover ricordare la formula della distanza punto-retta e di saper ragionare come visto sull’equazione irrazionale che ci ritroveremo a dover risolvere. Per cui a voi la scelta del metodo da utilizzare, come sempre tenendo conto delle indicazioni del vostro insegnante e/o libro di testo.
Esercizio 7
Determinare l’equazione della circonferenza passante per i punti {A=(-1,-3)} e {B=(-2,-2)} e tangente alla retta {r:12x+5y+9=0} nel punto {T=\left( -\dfrac{1}{13}, -\dfrac{21}{13}\right)}. Scrivere inoltre le equazioni delle rette tangenti alla circonferenza e passanti per il punto esterno {P=(-1,1)}.
Per poter determinare l’equazione della circonferenza in esame disponiamo delle coordinate di due punti ad essa appartenenti e dell’equazione di una retta ad essa tangente. Tali dati sono sufficienti per individuare univocamente una circonferenza nel piano (vedi: condizioni per determinare l’equazione di una circonferenza).
Infatti, noti due punti di una circonferenza, l’asse del segmento che ha per estremi tali punti passa necessariamente per il centro. Ma anche la retta perpendicolare alla tangente alla circonferenza in un punto e passante per il punto di tangenza passa per il centro. Di conseguenza, dall’intersezione tra le due rette sarà possibile ottenere le coordinate del centro della circonferenza stessa.
Cominciamo determinando l’equazione dell’asse del segmento avente per estremi i punti {A} e {B}. Prima di tutto, calcoliamo il punto medio del segmento, che è il punto per il quale passa l’asse del segmento stesso:
M_{AB}=\left( \dfrac{x_A+x_B}{2}, \dfrac{y_A+y_B}{2}\right)=\left( \dfrac{-1-2}{2}, \dfrac{-3-2}{2}\right)=\left( -\dfrac{3}{2},-\dfrac{5}{2}\right)A questo punto determiniamo il coefficiente angolare della retta passante per i punti {A} e {B}:
m_{AB}=\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{-2+3}{-2+1}=-1A questo punto possiamo determinare l’equazione dell’asse del segmento, tenendo conto che è la retta passante per {M_{AB}} e perpendicolare alla retta per i punti {A} e {B}. Quindi, il coefficiente angolare dell’asse del segmento è l’inverso dell’opposto di {m_{AB}}.
\begin{align*} &r_{AB}:y-y_{M_{AB}}=-\dfrac{1}{m_{AB}}(x-x_{M_{AB}})\\ \\ &\Rightarrow \:r_{AB}: y+\dfrac{5}{2}=-\dfrac{1}{-1} \cdot\left( x+\dfrac{3}{2}\right) \end{align*}Quindi in forma esplicita:
r_{AB}: y=x-1Questa è l’equazione per l’asse del segmento {\overline{AB}}, che è una retta passante per il centro della circonferenza.
Ora dobbiamo determinare l’equazione della retta {s} perpendicolare alla retta {r:12x+5y+9=0} e passante per il punto di tangenza {T=\left( -\dfrac{1}{13}, -\dfrac{21}{13}\right)}. Infatti, abbiamo bisogno dell’equazione di un’altra retta passante per il centro della circonferenza. Ma la perpendicolare ad una retta tangente alla circonferenza passante per il punto di tangenza è una retta che passa necessariamente per il centro della circonferenza.
Ricaviamo il coefficiente angolare della retta {r}. Per fare questo possiamo utilizzare la formula specifica oppure ricondurre l’equazione della retta stessa alla forma esplicita. Scegliamo la seconda strada. Abbiamo:
5y=-12x-9 \quad \Rightarrow \quad r: y=-\dfrac{12}{5}x-\dfrac{9}{5}Poiché l’equazione è della forma {y=mx+q}, il coefficiente angolare {m_r} della retta {r} è {m_r=-\dfrac{12}{5}}. Così, la retta perpendicolare a {r} e passante per {T=\left( -\dfrac{1}{13}, -\dfrac{21}{13}\right)} è:
s: y-y_T=-\dfrac{1}{m_r}(x-x_T)ovvero sostituendo i valori:
s:y+\dfrac{21}{13}=-\dfrac{1}{-\frac{12}{5}}\left( x+\dfrac{1}{13}\right)e quindi in forma esplicita:
\begin{align*} &y=\dfrac{5}{12}x +\dfrac{5}{12\cdot13}-\dfrac{21}{13}; \\ \\ & y=\dfrac{5}{12}x+\dfrac{5}{156}-\dfrac{21 \cdot 12}{156};\\ \\ & y=\dfrac{5}{12}x-\dfrac{247}{156};\\ \\ & s: y=\dfrac{5}{12}x-\dfrac{19}{12}\end{align*}A questo punto possiamo determinare le coordinate del centro della circonferenza come intersezione tra l’asse {r_{AB}} e la retta {s}:
\begin{cases} r_{AB}: y=x-1 \\ \\ s: y=\dfrac{5}{12}x-\dfrac{19}{12} \end{cases}Risolviamo il sistema con il metodo del confronto:
\small \begin{cases} x-1=\dfrac{5}{12}x-\dfrac{19}{12} \quad \rightarrow \: \left( 1-\dfrac{5}{12}\right)x=-\dfrac{19}{12}+1 \quad \rightarrow \: x=\dfrac{12}{7}\cdot \left( -\dfrac{7}{12} \right) \: \rightarrow \: x =-1\\ \\ y=\dfrac{5}{12}x-\dfrac{19}{12} \quad \rightarrow \: y=-\dfrac{5}{12}-\dfrac{19}{12} \quad \rightarrow \: y=-2\end{cases}Così il centro {C} della circonferenza è:
C=\left( -1, -2\right)
Per scrivere l’equazione della circonferenza ci serve ancora il raggio. Ma questo è dato ad esempio da:
r=\overline{AC}=\sqrt{(x_C-x_A)^2+(y_C-y_A)^2}=\sqrt{(-1+1)^2+(-2+3)^2}=1Ma disponendo ormai di centro e raggio possiamo scrivere l’equazione della circonferenza cercata come:
\begin{align*} &(x-x_C)^2+(y-y_C)^2=r^2; \\ \\ &\mathscr{C}:(x+1)^2+(y+2)^2=1\end{align*}ovvero in forma canonica:
\begin{align*} &x^2+2x+1+y^2+4y+4-1=0;\\ \\ & \mathscr{C}: x^2+y^2+2x+4y+4=0\end{align*}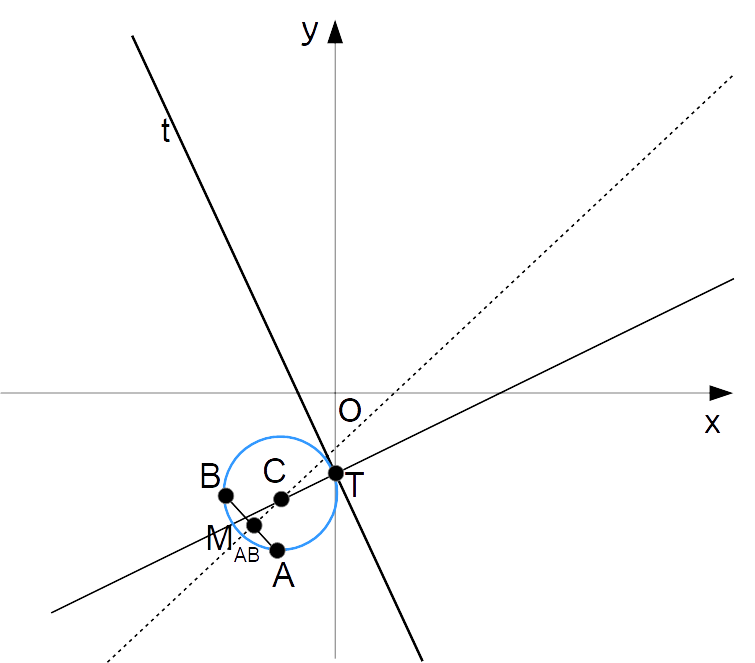
Ora dobbiamo determinare le equazioni delle rette tangenti alla circonferenza e passanti per il punto ad essa esterno {P=(-1,1)}. Utilizziamo il metodo basato sulla formula della distanza punto-retta.
Una generica retta tangente alla circonferenza e tale da passare per il punto {P=(-1,1)} avrà equazione:
t:y-1=m_t(x+1)
ove {m_t} è il coefficiente angolare della generica retta tangente alla circonferenza passante per {P}. L’equazione appena scritta diviene in forma implicita:
t:m_tx-y+m_t+1=0
La retta è ora della forma {ax+by+c=0} con {a=m_t, b=-1} e infine {c=m_t+1}.
Per ricercare i due valori del coefficiente angolare {m_t} (le rette tangenti ad una circonferenza per un punto esterno sono sempre due) imponiamo che la distanza fra la retta {t} e il centro {C} della circonferenza sia uguale al raggio:
d(t, C)=r
Ciò discende direttamente dalla definizione di distanza tra una retta e un punto nel piano. Utilizzando la formula della distanza punto-retta abbiamo:
\dfrac{|ax_C+by_C+c|}{\sqrt{a^2+b^2}}=rovvero, sostituendo i valori e sviluppando i calcoli:
\begin{align*} & \dfrac{|m_t\cdot(-1)+(-1) \cdot (-2)+m_t+1|}{\sqrt{m_t^2+(-1)^2}}=1; \\ \\ &\dfrac{|-m_t+2+m_t+1|}{\sqrt{m_t^2+1}}-1=0;\\ \\ & \dfrac{3-\sqrt{m_t^2+1}}{\sqrt{m_t^2+1}}=0;\\ \\ & \sqrt{m_t^2+1}=3; \\ \\ & m_t^2+1=9 \quad \Rightarrow \quad m_{t_{1,2}} = \pm \sqrt{8}=\pm 2\sqrt{2} \end{align*}A questo punto abbiamo ottenuto i valori dei coefficienti angolari delle rette tangenti alla circonferenza e passanti per il punto esterno {P}.
Riprendiamo per comodità l’equazione della generica retta tangente {t} alla circonferenza passante per il punto esterno {P}:
t:y-1=m_t(x+1)
L’equazione in forma esplicita diviene:
t:y=m_tx+m_t+1
Sostituendo i valori precedentemente ricavati per {m_t} nell’equazione della generica retta tangente {t} in forma esplicita otteniamo in conclusione le equazioni:
t_1: y=2\sqrt{2}x+2\sqrt{2}+1; \qquad t_2:y=-2\sqrt{2}x-2\sqrt{2}+1Esercizio 8
Determinare l’equazione della circonferenza {\mathscr{C}} concentrica alla circonferenza {\mathscr{C}'} di equazione {x^2+y^2+3x+6y-7=0} e tangente alla retta {s} di equazione {2x-3y+5=0}.
Cominciamo ricavando le coordinate del centro della circonferenza {\mathscr{C}'}. Ricordiamo che a partire dall’equazione in forma canonica di una circonferenza (reale non degenere):
x^2+y^2+ax+by+c=0
le coordinate del centro sono date da:
x_C=-\dfrac{1}{2}a, \qquad y_C=-\dfrac{1}{2}bNel nostro caso abbiamo l’equazione:
x^2+y^2+3x+6y-7=0
da cui segue {a=3} e {b=6}. Di conseguenza, per le coordinate del centro della circonferenza {\mathscr{C}_1} si ha:
x_C=-\dfrac{1}{2} \cdot 3=-\dfrac{3}{2}; \qquad y_C=-\dfrac{1}{2} \cdot 6=-3Ora, dato che le due circonferenze sono concentriche, le coordinate ottenute per il centro della circonferenza {\mathscr{C}'} sono anche relative al centro della circonferenza {\mathscr{C}}. Di conseguenza:
C=\left( -\dfrac{3}{2}, -3\right)A questo punto sono note le coordinate del centro della circonferenza {\mathscr{C}}, ma per scriverne l’equazione abbiamo anche bisogno del raggio della circonferenza.
Tuttavia, è nota l’equazione di una retta tangente alla circonferenza, ovvero l’equazione della retta {s}. Così, è possibile ricavare il raggio della circonferenza come distanza fra la retta {s} e il centro della circonferenza stessa.
Dall’equazione della retta {s}:
2x-3y+5=0
risultano i coefficienti:
a=2, \: b=-3, \: c=5
e quindi applicando la formula della distanza tra una retta e un punto del piano si ha:
\begin{align*} &r=d(s, C)=\dfrac{\left| ax_C+by_C+c\right|}{\sqrt{a^2+b^2}}=\dfrac{\left| 2 \cdot \left( -\dfrac{3}{2}\right)-3 \cdot (-3)+5\right|}{\sqrt{2^2+(-3)^2}}=\\ \\ & =\dfrac{11}{\sqrt{13}}\end{align*}Ma a questo punto disponendo delle coordinate del centro e della misura del raggio della circonferenza {\mathscr{C}} possiamo scriverne l’equazione nella forma con centro e raggio ed anche in forma canonica:
\begin{align*} & \left( x+\dfrac{3}{2}\right)^2+\left( y+3\right)^2=\left( \dfrac{11}{\sqrt{13}}\right)^2; \\ \\ & x^2+3x+\dfrac{9}{4}+y^2+6y+9-\dfrac{121}{13}=0;\\ \\ & x^2+y^2+3x+6y+\dfrac{9}{4}+9-\dfrac{121}{13}=0;\\ \\ & x^2+y^2+3x+6y+\dfrac{9\cdot13+9\cdot52-121\cdot4}{52}=0;\\ \\ & x^2+y^2+3x+6y+\dfrac{117+468-484}{52}=0;\\ \\ & \boxed{\mathscr{C}:x^2+y^2+3x+6y+\dfrac{101}{52}=0} \end{align*}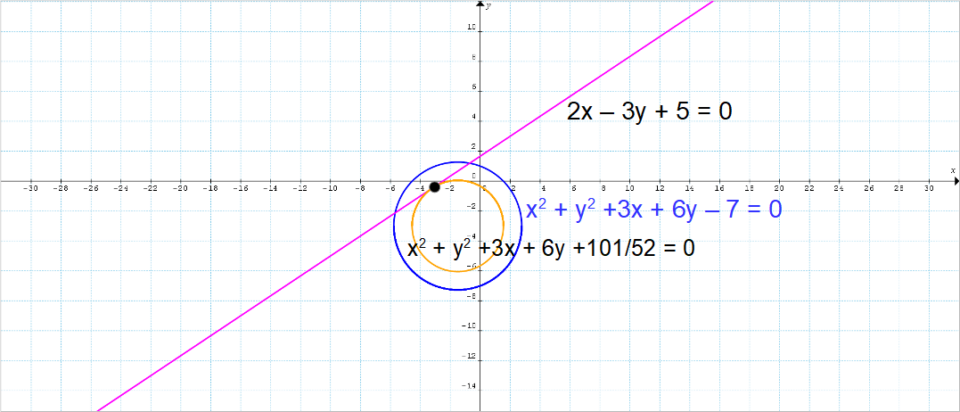
Concluso anche questo esercizio, ci mancano soltanto un paio di esercizi di riepilogo sulla circonferenza, prima di poterci salutare.
Esercizio 9
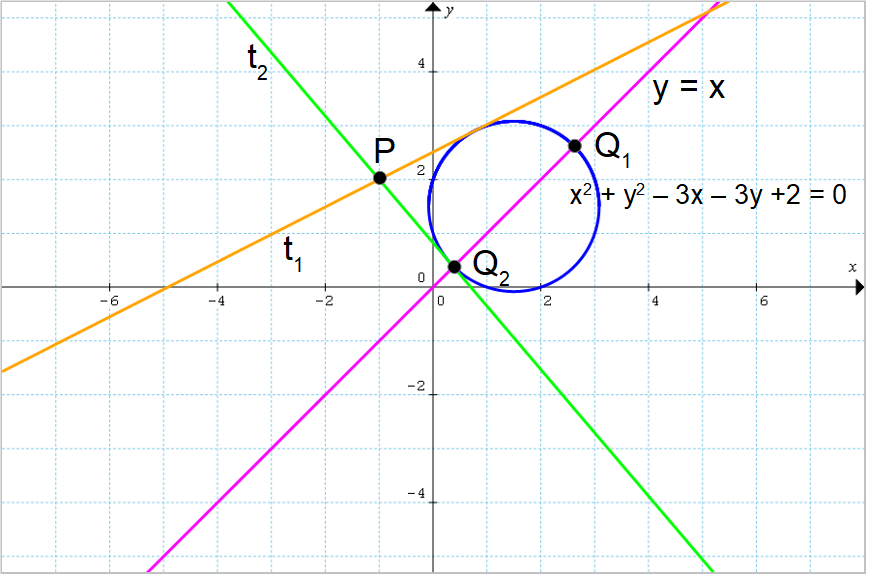
Determinare l’equazione della circonferenza {\mathscr{C}} passante per i punti {P_1=(1,0), P_2=(2,0), P_3=(0,2)} e calcolare le coordinate del suo centro. Determinare inoltre le coordinate dei punti di intersezione tra la circonferenza e la retta passante per l’origine e per il centro della circonferenza stessa. Infine, determinare le equazioni delle rette tangenti a {\mathscr{C}} condotte per il punto esterno {P=(-1,2)}.
Cominciamo determinando l’equazione della circonferenza. Poiché le ordinate dei primi due punti e l’ascissa del terzo punto sono nulle, ci aspettiamo che impostando il sistema con le condizioni di appartenenza dei punti alla circonferenza non otteniamo equazioni troppo complicate. Così scegliamo il metodo delle condizioni di appartenenza piuttosto che il metodo basato sulla ricerca di centro e raggio.
Dette con {x_1, y_1, x_2, y_2, x_3, y_3} le coordinate dei punti dati, impostiamo il sistema come segue:
\begin{cases} x_1^2+y_1^2+ax_1+by_1+c=0 \\ \\ x_2^2+y_2^2+ax_2+by_2+c=0 \\ \\ x_3^2+y_3^2+ax_3+by_3+c=0\end{cases}Sostituendo le coordinate dei punti:
\small \begin{cases} 1^2+a+c=0 \\ \\ 2^2+2a+c=0\\ \\ 2^2+2b+c=0\end{cases} \quad \Rightarrow \quad \begin{cases} a+c=-1 \quad \rightarrow \quad c=-1-a \\ \\ 2a+c=-4 \quad \rightarrow \quad 2a-1-a=-4 \quad \rightarrow \:a=-3\\ \\ 2b+c=-4 \quad \rightarrow \quad b=\dfrac{-4-c}{2} \end{cases}Sostituendo il valore ottenuto per {a} nella prima equazione, e quindi il valore che così si ottiene per {c} nella terza equazione, abbiamo per il sistema la soluzione:
\begin{cases} c=-1-a \quad \rightarrow \quad c=2 \\ \\ a=-3 \\ \\ b=\dfrac{-4-c}{2} \quad \rightarrow \quad b=-3\end{cases}Disponendo dei coefficienti {a,b,c} possiamo scrivere l’equazione in forma canonica della circonferenza {\mathscr{C}}:
\mathscr{C}: x^2+y^2-3x-3y+2=0Le coordinate del centro della circonferenza si ricavano agevolmente a partire dai coefficienti {a} e {b}, ovvero i coefficienti dei termini in {x} e {y}:
x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot (-3)=\dfrac{3}{2}; \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot (-3)=\dfrac{3}{2}Così il centro della circonferenza è:
C=\left( \dfrac{3}{2}, \dfrac{3}{2}\right)Il quesito successivo richiede di determinare i punti di intersezione tra la circonferenza {\mathscr{C}} e la retta passante per l’origine e per il punto {C}.
Cominciamo scrivendo l’equazione della retta passante per l’origine e per il centro {C} della circonferenza (formula della retta per due punti):
\dfrac{y-y_C}{y_O-y_C}=\dfrac{x-x_C}{x_O-x_C}ovvero sostituendo i valori:
\dfrac{y-\dfrac{3}{2}}{0-\dfrac{3}{2}}=\dfrac{x-\dfrac{3}{2}}{0-\dfrac{3}{2}}da cui si ottiene in conclusione l’equazione:
y=x
A questo punto, per determinare i punti di intersezione con la circonferenza {\mathscr{C}} basta risolvere il seguente sistema, contenente le equazioni rispettivamente della circonferenza e della retta:
\begin{cases} x^2+y^2-3x-3y+2=0 \\ \\ y=x \end{cases}Operando per sostituzione si ha:
x^2+x^2-3x-3x+2=0 \quad \Rightarrow \quad 2x^2-6x+2=0
ovvero:
x^2-3x+1=0
Risolvendo l’equazione di secondo grado otteniamo i seguenti valori delle ascisse:
x_{1,2}=\dfrac{3 \pm \sqrt{(-3)^2-4 \cdot 1 \cdot 1}}{2}=\dfrac{3\pm \sqrt{5}}{2}Tenendo conto che per la seconda equazione a sistema l’ascissa e l’ordinata di ciascun punto di intersezione sono tra loro uguali, otteniamo i punti di intersezione:
Q_1=\left( \dfrac{3+\sqrt{5}}{2}, \dfrac{3+\sqrt{5}}{2}\right); \qquad Q_2=\left( \dfrac{3-\sqrt{5}}{2}, \dfrac{3-\sqrt{5}}{2}\right)Rimangono a questo punto da determinare le equazioni delle rette tangenti alla circonferenza {\mathscr{C}} condotte per il punto esterno {P=(-1,2)}.
La generica retta tangente alla circonferenza passante per il punto {P} ha equazione:
t:y-2=m_t(x+1)
ovvero in forma esplicita:
t:y=m_tx+m_t+2
e in forma implicita:
t:m_tx-y+m_t+2=0
Utilizziamo la formula della distanza tra una retta ed un punto. Come già visto in precedenza, l’idea è quella di imporre che la distanza fra la retta tangente e il centro {C} della circonferenza sia uguale al raggio della circonferenza stessa.
Per il raggio della circonferenza abbiamo, tenendo conto dell’equazione della circonferenza e delle coordinate del suo centro:
r=\sqrt{x_C^2+y_C^2-c}=\sqrt{\left( \dfrac{3}{2}\right)^2+\left( \dfrac{3}{2}\right)^2-2}=\sqrt{\dfrac{5}{2}}=\dfrac{\sqrt{10}}{2}Ora, utilizzando l’equazione in forma implicita della generica retta {t}, imponiamo l’uguaglianza:
d(t,C)=r
che riscritta tenendo conto dell’equazione in forma implicita della retta {t}, delle coordinate del centro {C} e del raggio della circonferenza, diviene:
\begin{align*} & \dfrac{\left|m_t\cdot\dfrac{3}{2}-1 \cdot \dfrac{3}{2}+m_t+2\right|}{\sqrt{m_t^2+1}}=\dfrac{\sqrt{10}}{2}; \\ \\ & \dfrac{\dfrac{5}{2}m_t+\dfrac{1}{2}}{\sqrt{m_t^2+1}}-\dfrac{\sqrt{10}}{2}=0;\\ \\ &\dfrac{5m_t+1-\sqrt{10}\sqrt{m_t^2+1}}{2\sqrt{m_t^2+1}}=0;\\ \\ & 5m_t+1=\sqrt{10}\sqrt{m_t^2+1}; \\ \\ & (5m_t+1)^2=10 \cdot (m_t^2+1);\\ \\ & 25m_t^2+10m_t+1-10m_t^2-10=0;\\ \\ & 15m_t^2+10m_t-9=0 \end{align*}Risolvendo l’equazione di secondo grado otteniamo per il coefficiente della retta tangente {t} i valori:
\begin{align*} & m_{t_{1,2}}=\dfrac{-5 \pm \sqrt{5^2-15 \cdot(-9)}}{15}=\dfrac{-5 \pm \sqrt{25+15 \cdot 9}}{15}=\\ \\ & =\dfrac{-5 \pm \sqrt{160}}{15}=\dfrac{-5 \pm 4\sqrt{10}}{15} \end{align*}Di conseguenza sostituendo i valori di {m_t} appena calcolati abbiamo le seguenti equazioni per le rette tangenti alla circonferenza {\mathscr{C}} passanti per il punto {P}:
t_1: y-2=\dfrac{-5+4\sqrt{10}}{15}(x+1); \qquad t_2:y-2=\dfrac{-5-4\sqrt{10}}{15}(x+1)Qui è risultato conveniente esprimere le equazioni delle rette tangenti nella forma:
t:y-2=m_t(x+1)
Visto come si presenta il coefficiente angolare, risulterebbe infatti piuttosto scomodo ricondurre le equazioni alla forma {y=mx+q}.
Esercizio 10
Veniamo ora finalmente all’ultimo di questa serie di esercizi di riepilogo sulla circonferenza.
Data la retta {s} di equazione {2x+y-2=0}, determinare l’equazione della circonferenza {\mathscr{C}} avente per diametro il segmento staccato sulla retta {s} dagli assi cartesiani. Determinare inoltre le equazioni delle rette parallele alla retta {s} e tali da essere tangenti alla circonferenza {\mathscr{C}}.
Cominciamo determinando i punti di intersezione tra la retta {s} e gli assi cartesiani. Il segmento avente per estremi i punti di intersezione ottenuti sarà il diametro della circonferenza la cui equazione è da determinare.
Ricordiamo che l’asse {x} ha equazione:
y=0
mentre l’asse {y} ha equazione:
x=0
Si tratta in particolare delle due rette orizzontali e verticali tali da passare per l’origine.
Cominciamo determinando il punto di intersezione tra la retta {s} e l’asse {x} (vedi: intersezione tra due rette):
\begin{cases} 2x+y-2=0 \\ \\ y=0\end{cases} \quad \Rightarrow \quad \begin{cases} x=1 \\ \\ y=0\end{cases}Proseguiamo determinando il punto di intersezione tra la retta {s} e l’asse {y}:
\begin{cases} 2x+y-2 = 0\\ \\ x=0\end{cases} \quad \Rightarrow \quad \begin{cases} y=2 \\ \\ x=0\end{cases}Così i due punti di intersezione cercati, ciascuno corrispondente alle coppie di valori per {x} ed {y} ottenuti, sono:
T_1=(1,0); \qquad T_2=(0,2)
Ciò che ora dobbiamo fare è determinare l’equazione della circonferenza avente per diametro il segmento {\overline{T_1T_2}}, ovvero il segmento avente per estremi i due punti di intersezione appena ottenuti.
In base all’esercizio 2, potremmo direttamente utilizzare la formula:
x^2+y^2+(-x_A-x_B)x+(-y_A-y_B)y+x_Ax_B+y_Ay_B=0
che nel nostro caso diviene:
x^2+y^2+(-x_{T_1}-x_{T_2})x+(-y_{T_1}-y_{T_2})y+x_{T_1}x_{T_2}+y_{T_1}y_{T_2}=0e quindi sostituendo i valori:
\begin{align*} &x^2+y^2+(-1-0)x+(-0-2)y+1\cdot0+0\cdot2=0;\\ \\ & \boxed{\mathscr{C}: x^2+y^2-x-2y=0}\end{align*}Ovviamente la formula utilizzata è un po’ scomoda da ricordare, ma è comunque possibile utilizzare il metodo alternativo sempre visto nell’esercizio 2. Ricordiamo infatti che se un segmento di dati estremi è il diametro di una circonferenza, il centro della circonferenza stessa è dato dal punto medio del segmento. Infine, il raggio si ottiene come distanza del centro da uno dei due estremi del segmento. E noti centro e raggio, è possibile scrivere l’equazione della circonferenza.
In ogni caso, per ricordare la formula basta tenere conto che dobbiamo scrivere l’equazione in forma canonica di una circonferenza ove:
- i coefficienti dei termini in {x} e {y} sono le somme rispettivamente delle ascisse e delle ordinate degli estremi del diametro, cambiate di segno;
- il termine noto è dato dalla somma dei prodotti rispettivamente delle ascisse e delle ordinate degli estremi del diametro.
Passiamo ora all’ultimo quesito. Vediamo in particolare come determinare le equazioni delle rette tangenti alla circonferenza e parallele alla retta {s}.
Nel risolvere il problema occorre stare particolarmente attenti alla strada che si sceglie. E’ molto importante fare un semplice disegno e tenere ben presenti le proprietà della geometria elementare. In particolare, in questo caso occorre ricordare che la perpendicolare alla retta tangente ad una circonferenza passante per il punto di tangenza, passa anche per il centro della circonferenza stessa.
Ora, poiché ciascuna retta tangente dovrà essere parallela alla retta {s}, il relativo coefficiente angolare è noto. Infatti, basterà ricavare il coefficiente angolare della retta {s}. E questo sarà il valore del coefficiente angolare anche delle rette tangenti.
L’equazione della retta {s} è:
s: 2x+y-2=0
che riscritta in forma esplicita diviene:
s: y=-2x+2
da cui segue il valore del coefficiente angolare:
m_s=-2
Così, la generica retta tangente alla circonferenza {\mathscr{C}} e parallela alla retta {s} avrà equazione:
t:y-y_T=m_s(x-x_T)
ovvero, sostituendo il valore di {m_s}:
t:y-y_T=-2(x-x_T)
ove {x_T} ed {y_T} sono le coordinate di ciascuno dei punti di tangenza {T_1'} e {T_2'}, al momento sconosciute.
Ora, la retta {s'} passante per il centro e per i punti di tangenza alla circonferenza è perpendicolare alla rette tangenti. Di conseguenza, per quanto sappiamo sulla relazione di perpendicolarità fra rette abbiamo:
m_{s'}=-\dfrac{1}{m_s}=-\dfrac{1}{-2}=\dfrac{1}{2}e la retta {s'}, passando per il centro della circonferenza, avrà equazione:
s':y-y_C=m_{s'}\left( x-x_C\right)Le coordinate del centro della circonferenza {x_C} ed {y_C} si possono agevolmente ricavare a partire dalla equazione della circonferenza stessa:
x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot(-1)=\dfrac{1}{2}; \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot (-2)=1e quindi sostituendo tali valori nell’equazione di {s'}:
s': y-1=\dfrac{1}{2} \left( x-\dfrac{1}{2}\right)ovvero in forma esplicita:
s': y=\dfrac{1}{2}x+\dfrac{3}{4}Così, per determinare le coordinate dei punti di contatto della circonferenza rispetto alla rette ad essa tangenti e parallele ad {s}, l’idea è quella di intersecare la circonferenza con la retta {s'}. Ciò ha senso poiché ogni retta tangente alla circonferenza e parallela ad {s} ha in comune con la retta {s'} i punti di contatto con la circonferenza.
Occorre quindi impostare il sistema:
\begin{cases} \mathscr{C}: x^2+y^2-x-2y=0 \\ \\ s': y=\dfrac{1}{2}x+\dfrac{3}{4} \end{cases}Si tratta di un sistema non lineare, ma la sua risoluzione non è affatto complicata. Effettivamente basta sostituire l’espressione di {y}, fornita dalla seconda equazione, nella prima equazione. Considerando separatamente la prima equazione abbiamo in particolare:
\begin{align*} &x^2+\left( \dfrac{1}{2}x+\dfrac{3}{4}\right)^2-x-2\left( \dfrac{1}{2}x+\dfrac{3}{4}\right)=0; \\ \\ & x^2+\dfrac{1}{4}x^2+\dfrac{3}{4}x+\dfrac{9}{16}-x-x-\dfrac{3}{2}=0;\\ \\ & \dfrac{5}{4}x^2-\dfrac{5}{4}x-\dfrac{15}{16}=0; \\ \\ & 20x^2-20x-15=0;\\ \\ & 4x^2-4x-3=0\end{align*}Abbiamo così ottenuto un’equazione di secondo grado che, una volta risolta, fornisce i valori delle ascisse dei punti di contatto della circonferenza {\mathscr{C}} con le rette ad essa tangenti e parallele ad {s}. Utilizzando la formula ridotta:
\begin{align*} &x_{1,2}=\dfrac{2 \pm \sqrt{4-4 \cdot (-3)}}{4}=\dfrac{2 \pm 4}{4}=\begin{cases} \dfrac{3}{2}\\ \\ -\dfrac{1}{2}\end{cases}\end{align*}da cui {x_1=\dfrac{3}{2}} e {x_2=-\dfrac{1}{2}}.
Per ricavare le ordinate dei punti di tangenza (o punti di contatto) basta sostituire i valori appena ottenuti nell’equazione:
y=\dfrac{1}{2}x+\dfrac{3}{4}ottenendo, rispettivamente:
y_1=\dfrac{1}{2} \cdot \dfrac{3}{2}+\dfrac{3}{4} \quad \rightarrow \quad y_1= \dfrac{3}{2}e:
y_2=\dfrac{1}{2} \cdot \left( -\dfrac{1}{2}\right)+\dfrac{3}{4} \quad \rightarrow \quad y_2=\dfrac{1}{2}Abbiamo quindi in conclusione i punti di tangenza:
T_1'=\left( x_1, y_1\right)=\left( \dfrac{3}{2}, \dfrac{3}{2}\right); \qquad T_2'=(x_2,y_2)=\left( -\dfrac{1}{2}, \dfrac{1}{2}\right)A questo punto, note le coordinate dei punti di contatto (o punti di tangenza) possiamo infine scrivere le equazioni delle rette tangenti corrispondenti, a partire dall’equazione della generica retta tangente {t}, che per comodità riportiamo:
t:y-y_T=-2(x-x_T)
Abbiamo:
\begin{align*} &t_1: y-\dfrac{3}{2}=-2\left( x-\dfrac{3}{2}\right); \\ \\ & t_2: y-\dfrac{1}{2}=-2\left( x+\dfrac{1}{2}\right)\end{align*}ovvero in forma esplicita:
\begin{align*} &t_1: y=-2x+\dfrac{9}{2} ; \qquad t_2: y=-2x-\dfrac{1}{2}\end{align*}L’esercizio è così concluso.
Nel risolvere l’ultimo quesito dell’esercizio, ovvero la determinazione delle equazioni delle rette tangenti alla circonferenza e parallele ad {s}, abbiamo cercato di percorrere la strada più breve, facendo uso delle proprietà elementari della circonferenza.
Differenti strade avrebbero portato ad uno svolgimento dell’esercizio ben più pesante. Ci riferiamo in particolare all’utilizzo della distanza punto-retta, oppure in alternativa all’utilizzo della condizione di determinante nullo dell’equazione risolvente il sistema relativo all’intersezione fra la circonferenza e ciascuna retta tangente. In quest’ultimo caso, in particolare, si ottiene un’equazione di secondo grado in due incognite che deve essere messa a sistema con un’altra condizione (l’appartenenza del generico punto di tangenza alla circonferenza – assolutamente improponibile – o, decisamente meglio, l’appartenenza del generico punto di tangenza alla retta {s'}).
Vediamo a puro scopo illustrativo l’applicazione del metodo del sistema risolvente, in modo da mettere in evidenza l’importanza della scelta della procedura risolutiva più breve negli esercizi sulla circonferenza e più in generale nei problemi di geometria analitica.
Cominciamo indicando con {T=(x_T, y_T)} il punto di tangenza tra la circonferenza e ciascuna retta tangente {t_1} e {t_2}.
Ora, dato che ciascuna retta tangente dovrà essere parallela alla retta {s}, ognuna di esse dovrà avere lo stesso coefficiente angolare della retta {s} (vedi: rette parallele). Come già fatto nello svolgimento precedente, determiniamo il coefficiente angolare della retta {s}:
s: 2x+y-2=0 \quad \Rightarrow \quad y=-2x+2 \quad \Rightarrow \quad m_s=-2
La generica retta tangente alla circonferenza e parallela ad {s} avrà quindi per tutto quanto detto equazione:
t: y-y_T=m_s(x-x_T)
ovvero:
t:y-y_T=-2(x-x_T)
e quindi in forma esplicita:
t:y=-2x+2x_T+y_T
Ora, scriviamo il sistema necessario a determinare i punti di intersezione tra la circonferenza {\mathscr{C}} e la generica retta tangente {t}:
\begin{cases}x^2+y^2-x-2y=0 \\ \\ y=-2x+2x_T+y_T \end{cases}La seconda equazione offre un’espressione per {y}, che sostituita nella prima equazione fornisce l’equazione risolvente del sistema:
\begin{align*} &x^2+(-2x+2x_T+y_T)^2-x-2\left( -2x+2x_T+y_T\right)=0;\\ \\ & x^2+4x^2+4x_T^2+y_T^2-8x_Tx-4y_Tx+4x_Ty_T-x+4x-4x_T-2y_T=0;\\ \\ & (1+4)x^2+(-8x_T-4y_T-1+4)x+4x_T^2+y_T^2+4x_Ty_T-4x_T-2y_T=0; \\ \\ & 5x^2+(-8x_T-4y_T+3)x+4x_T^2+y_T^2+4x_Ty_T-4x_T-2y_T=0\end{align*}Ora, dato che la circonferenza e la retta sono tangenti, imponiamo la condizione di determinante nullo dell’equazione risolvente:
\small \begin{align*} &\dfrac{(-8x_T-4y_T+3)^2-4 \cdot 5 \cdot (4x_T^2+y_T^2+4x_Ty_T-4x_T-2y_T)}{2\cdot5}=0;\\ \\ & \dfrac{64x_T^2+16y_T^2+9+64x_Ty_T-48x_T-24y_T-80x_T^2-20y_T^2-80x_Ty_T+80x_T+40y_T}{10}=0;\\ \\ &(64-80)x_T^2+(-48+80)x_T+(16-20)y_T^2+(-24+40)y_T+(64-80)x_Ty_T+9=0; \\ \\ & -16x_T^2+32x_T-4y_T^2+16y_T-16x_Ty_T+9=0 \end{align*}L’equazione è nelle due incognite {x_T} ed {y_T}, e quindi non è direttamente risolvibile. Tuttavia, possiamo ricavare agevolmente un’altra equazione contenente le incognite {x_T} ed {y_T} osservando che il punto {T} appartiene alla retta {s'}, la cui equazione abbiamo scritto nello svolgimento precedente. Di conseguenza, tenendo conto dell’equazione della retta {s'}, dovrà anche valere la condizione di appartenenza:
s': y_T=\dfrac{1}{2}x_T+\dfrac{3}{4} Imponendo così contemporaneamente la condizione di determinante nullo del sistema risolvente e la condizione di appartenenza del punto {T} alla retta {s} abbiamo il seguente sistema:
\begin{cases} -16x_T^2+32x_T-4y_T^2+16y_T-16x_Ty_T+9=0 \\ \\ y_T=\dfrac{1}{2}x_T+\dfrac{3}{4} \end{cases}Sostituendo l’espressione di {y_T} nella prima equazione abbiamo:
\small \begin{align*} &-16x_T^2+32x_T-4\left( \dfrac{1}{2}x_T+\dfrac{3}{4}\right)^2+16\left( \dfrac{1}{2}x_T+\dfrac{3}{4}\right)-16x_T\left( \dfrac{1}{2}x_T+\dfrac{3}{4}\right)+9=0;\\ \\ &-16x_T^2+32x_T-4\left( \dfrac{1}{4}x_T^2+\dfrac{3}{4}x_T+\dfrac{9}{16}\right)+8x_T+12-8x_T^2-12x_T+9=0;\\ \\ & -16x_T^2+32x_T-x_T^2-3x_T-\dfrac{9}{4}+8x_T+12-8x_T^2-12x_T+9=0;\\ \\ & (-16-1-8)x_T^2+(32-3+8-12)x_T-\dfrac{9}{4}+12+9=0;\\ \\ & -25x_T^2+25x_T+\dfrac{75}{4}=0;\\ \\ & 100x_T^2-100x_T-75=0; \\ \\ & 4x_T^2-4x_T-3=0 \end{align*}Ritroviamo così l’equazione di secondo grado già vista nello svolgimento precedente, la quale fornisce i valori delle ascisse dei punti di tangenza {T_1} e {T_2} già determinati.
Visti i calcoli ben più pesanti che ci siamo ritrovati a dover eseguire applicando questo secondo metodo, sottolineiamo ancora l’importanza della scelta del metodo risolutivo più efficiente negli esercizi sulla circonferenza e nei problemi di geometria analitica in generale.
Per quanto riguarda questa serie di esercizi di riepilogo sulla circonferenza è tutto. Ricordiamo le lezioni sulla circonferenza e le esercitazioni correlate per poter rivedere tutti gli argomenti affrontati negli esercizi.
Un saluto a tutti voi e buon proseguimento, come sempre, con SìMatematica!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
