Esercizi sui fasci di circonferenze

 - 

Esercizi sulla circonferenza (scuole superiori)

In questa scheda proponiamo una serie di esercizi svolti e commentati sui fasci di circonferenze. In particolare, qui potrete trovare le applicazioni pratiche di quanto visto nella lezione teorica sui fasci di circonferenze.

Riassumendo in breve la teoria, abbiamo visto che l’equazione di un fascio di circonferenze si può ottenere come combinazione lineare delle equazioni in forma canonica di due particolari circonferenze, dette circonferenze generatrici. Nello specifico, date due circonferenze {\mathscr{C}_1: x^2+y^2+a_1x+b_1y+c_1=0} e {\mathscr{C}_2: x^2+y^2+a_2x+b_2y+c_2=0}, l’equazione del fascio di circonferenze corrispondente è:

x^2+y^2+a_1x+b_1y+c_1+k(x^2+y^2+a_2x+b_2y+c_2)=0 \qquad (1)

ove {k} è un parametro reale.

In alternativa, tale equazione si può anche esprimere nella forma:

(1+k)x^2+(1+k)y^2+(a_1+ka_2)x+(b_1+kb_2)y+c_1+kc_2=0 \qquad (2)

con {k \neq -1}.

Infine, è anche possibile in generale ridurre l’equazione del fascio alla combinazione lineare dell’equazione di una delle due circonferenze generatrici e dell’equazione dell’asse radicale del fascio. L’equazione dell’asse radicale del fascio, in particolare, si ottiene dall’ultima equazione scritta per {k= -1}:

(a_1-a_2)x+(b_1-b_2)y+c_1-c_2=0 \qquad (3)

Così è possibile scrivere l’equazione del fascio ad esempio come:

\small x^2+y^2+a_1x+b_1y+c_1+h\left[ (a_1-a_2)x+(b_1-b_2)y+c_1-c_2\right]=0 \qquad (4)

ove {h} è ancora un parametro reale.

Per svolgere gli esercizi sui fasci di circonferenze, è inoltre importante ricordare che esistono i seguenti casi:

• se le circonferenze generatrici sono secanti, queste si intersecano nei due punti {A} e {B} che sono i punti base del fascio. Le circonferenze del fascio sono tutte secanti e passano per i punti base;
• se le circonferenze generatrici sono invece tangenti ad una stessa retta nel punto {A}, tutte le circonferenze del fascio risulteranno tangenti a quella stessa retta nel medesimo punto {A}. Quest’ultimo è l’unico punto base del fascio;
• ancora, se le circonferenze generatrici sono concentriche, ovvero condividono lo stesso centro, allora tutte le circonferenze del fascio saranno concentriche. Il fascio non è in questo caso caratterizzato da alcun punto base.
• infine, se le circonferenze generatrici non hanno punti in comune e non sono concentriche, anche le circonferenze del fascio non si intersecheranno in alcun punto e non condivideranno lo stesso centro. Come nel caso precedente, il fascio non avrà alcun punto base.

Per classificare un fascio la cui equazione è data, l’idea è quella di ricondurre l’equazione del fascio alle forme {1} oppure {4}, e quindi determinare gli eventuali punti base del fascio. Tali punti, se esistono, si ottengono mettendo a sistema le equazioni delle circonferenze generatrici oppure l’equazione di una circonferenza generatrice e l’equazione dell’asse radicale. Se si ottengono due punti base il fascio sarà dato da circonferenze secanti, mentre se si ottiene un solo punto base il fascio sarà dato da circonferenze tangenti ad una stessa retta, che è l’asse radicale del fascio.

Nel caso in cui non si ottenga invece alcun punto base, il fascio potrà essere dato da circonferenze concentriche, oppure da circonferenze non concentriche e prive di punti in comune. Un fascio di circonferenze concentriche è facilmente riconoscibile dal fatto che le equazioni delle due circonferenze generatrici condividono gli stessi coefficienti dei termini in {x} e {y}. Ciò è immediata conseguenza del fatto che le coordinate del centro di una circonferenza dipendono proprio da tali coefficienti (vedi: equazione della circonferenza).

Passiamo a questo punto a svolgere insieme gli esercizi sui fasci di circonferenze, affrontando i vari casi appena ricordati.

Esercizi sui fasci di circonferenze svolti e commentati

Esercizio 1 (fascio di circonferenze secanti)

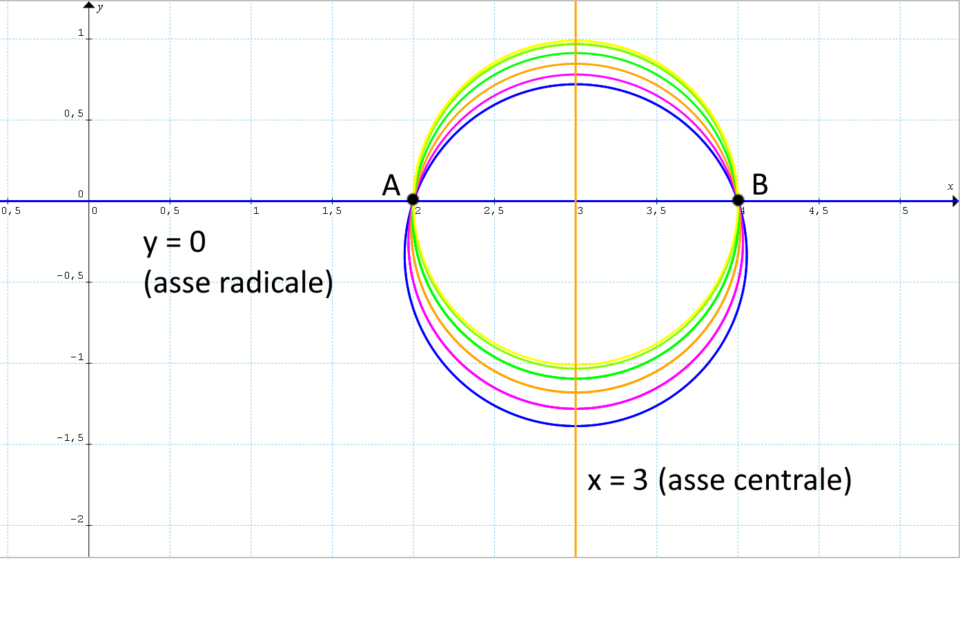
Studiare il fascio di circonferenze le cui circonferenze generatrici sono {\mathscr{C}_1: x^2+y^2-6x+2y+8=0} e {\mathscr{C}_2:x^2+y^2-6x+8=0}.

Lo studio di un fascio di circonferenze comprende le seguenti fasi:

• scrivere, se non è già data, l’equazione del fascio, in almeno una delle possibili forme;
• classificare il fascio, ovvero stabilire se è un fascio di circonferenze secanti, tangenti, concentriche oppure non concentriche e prive di punti in comune;
• determinare se esistono le coordinate dei punti base del fascio;
• infine, determinare ove possibile l’equazione dell’asse radicale e dell’asse centrale.

Nel nostro caso sono date le equazioni in forma canonica delle circonferenze generatrici. Pertanto, possiamo scrivere agevolmente l’equazione del fascio nella forma {1}:

x^2+y^2+a_1x+b_1y+c_1+k(x^2+y^2+a_2x+b_2y+c_2)=0

Nel nostro caso, utilizzando i primi membri delle equazioni delle circonferenze generatrici date:

x^2+y^2-6x+2y+8+k(x^2+y^2-6x+8)=0

Possiamo anche esprimere l’equazione del fascio nella forma {2}. Per fare ciò, senza dover ricordare la {(2)} a memoria, basta calcolare il prodotto, riordinare i termini e quindi eseguire dei raccoglimenti parziali per i termini in {x^2, y^2, x, y}:

\begin{align*} &x^2+y^2-6x+2y+8+kx^2+ky^2-6kx+8k=0; \\ \\ &x^2+kx^2+y^2+ky^2-6x-6kx+2y+8+8k=0; \\ \\ & \boxed{(1+k)x^2+(1+k)y^2+(-6-6k)x+2y+8(1+k)=0}\end{align*}

Per classificare il fascio, mettiamo a sistema le equazioni delle circonferenze generatrici, al fine di ricercare gli eventuali punti base.

\begin{cases} x^2+y^2-6x+2y+8=0 \\ \\ x^2+y^2-6x+8=0\end{cases}

Conviene risolvere il sistema per riduzione. Infatti, l’equazione che così si ottiene sarà eventualmente l’equazione dell’asse radicale del fascio. Possiamo ad esempio sostituire la prima equazione del sistema con l’equazione che si ottiene sottraendo membro a membro la seconda equazione alla prima. Osserviamo che i termini di secondo grado così facendo si cancellano l’uno con l’altro, per cui nello scrivere la nuova equazione possiamo direttamente ometterli. Si ha:

\begin{cases} \cancel{-6x}+2y+\cancel{8}+\cancel{6x}-\cancel{8}=0 \quad \rightarrow \quad 2y=0 \quad \rightarrow \quad \boxed{y=0} \\ \\ x^2+y^2-6x+8=0\end{cases}

Sostituiamo il valore ottenuto per la {y} nella seconda equazione:

\begin{cases} y=0 \\ \\ x^2-6x+8=0\end{cases}

Risolviamo l’equazione di secondo grado (formula ridottissima):

x_{1,2}=3 \pm \sqrt{(-3)^2-8}=3 \pm 1 = \begin{cases} 4 \\ \\ 2\end{cases}

Di conseguenza abbiamo per il fascio i punti base:

A=(2,0); \qquad B=(4,0)

Il fascio di circonferenze è dato da circonferenze secanti (due punti base) e l’equazione dell’asse radicale è quella evidenziata nel sistema, ovvero:

r_{AB}: y=0

L’asse centrale è perpendicolare all’asse radicale, e sarà quindi in questo caso un’equazione della forma:

x=c

con {c} numero reale. Inoltre, l’asse centrale deve passare per i centri delle circonferenze generatrici.

Ricordiamo che data l’equazione in forma canonica di una circonferenza, {x^2+y^2+ax+by+c=0} per le coordinate del centro {C=(x_C, y_C)} si ha:

x_C=-\dfrac{1}{2}a, \quad y_C=-\dfrac{1}{2}b

Dalle equazioni delle circonferenze generatrici abbiamo:

\begin{align*} & x_{C_1}=-\dfrac{1}{2}a_1=-\dfrac{1}{2} \cdot (-6)=3; \qquad y_{C_1}=-\dfrac{1}{2}b_1=-\dfrac{1}{2} \cdot 2 = -1 \\ \\ & x_{C_2} = -\dfrac{1}{2}a_2=-\dfrac{1}{2}\cdot(-6)=3; \qquad y_{C_2}=-\dfrac{1}{2} \cdot b_2=-\dfrac{1}{2} \cdot 0=0 \end{align*}

Così i centri delle circonferenze generatrici sono:

C_1=(3,-1); \qquad C_2=(3,0)

e l’equazione dell’asse centrale, ovvero della retta verticale passante per i centri delle circonferenze generatrici, sarà in conclusione:

r_C: x=3

Proseguiamo gli esercizi sui fasci di circonferenze con il caso di un fascio di circonferenze tangenti.

Esercizio 2 (fascio di circonferenze tangenti)

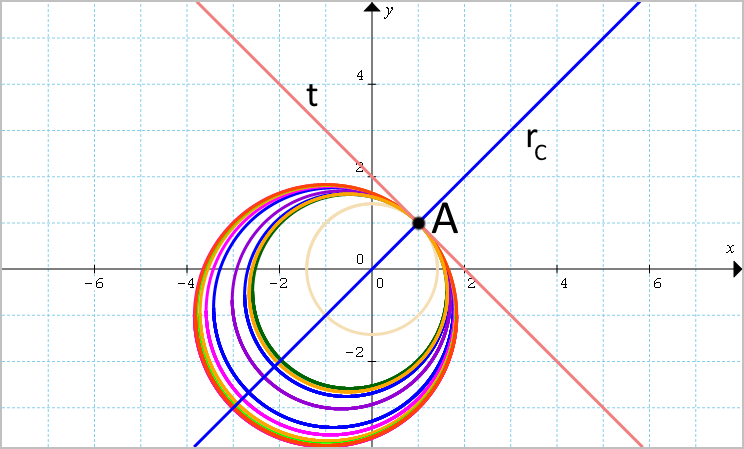
Studiare il fascio le cui circonferenze generatrici sono {\mathscr{C}_1: x^2+y^2+x+y-4=0} e {\mathscr{C}_2: x^2+y^2+2x+2y-6=0}.

Scriviamo l’equazione del fascio ad esempio nella forma {1}:

x^2+y^2+x+y-4+k\left( x^2+y^2+2x+2y-6\right)=0

In alternativa possiamo scrivere l’equazione del fascio anche nella forma {2}:

\begin{align*} &x^2+y^2+x+y-4+kx^2+ky^2+2kx+2ky-6k=0; \\ \\ & x^2+kx^2+y^2+ky^2+x+2kx+y+2ky-4-6k=0;\\ \\ & \boxed{(1+k)x^2+(1+k)y^2+(1+2k)x+(1+2k)y+2(-2-3k)=0}\end{align*}

Per classificare il fascio ricerchiamo gli eventuali punti di intersezione tra le circonferenze generatrici:

\begin{cases} x^2+y^2+x+y-4=0 \\ \\ x^2+y^2+2x+2y-6=0 \end{cases}

Risolvendo il sistema per riduzione come nell’esercizio precedente:

\begin{cases} x+y-4-2x-2y+6=0 \\ \\ x^2+y^2+2x+2y-6=0\end{cases}

ovvero:

\small\begin{cases}\boxed{ -x-y+2=0 }\quad \rightarrow \quad x=2-y \\ \\ x^2+y^2+2x+2y-6=0  \quad \rightarrow (2-y)^2+y^2+2(2-y)+2y-6=0\end{cases}

Eseguiamo i calcoli nella seconda equazione, e quindi risolviamola rispetto ad {y}:

\begin{align*} &4-4y+y^2+y^2+4-\cancel{2y}+\cancel{2y}-6=0; \\ \\ & 2y^2-4y+2=0;\\ \\ & y^2-2y+1=0; \\ \\ & y_{1,2}=1\pm \sqrt{1-1}=1\end{align*}

Otteniamo per {y} due valori reali e coincidenti, quindi a lato pratico il solo valore {y=1}. Sostituendo nella prima equazione a sistema il valore appena calcolato otteniamo per la {x}:

x=2-y=2-1=1

Il fascio ha quindi un solo punto base dato da:

A=(1,1)

Di conseguenza, avendo un solo punto base concludiamo che il fascio di circonferenze in esame è del tipo con circonferenze tangenti. In particolare, le circonferenze del fascio sono tutte tangenti nel punto {A} alla retta di equazione:

t: -x-y+2=0

ovvero:

t: x+y-2=0

Tale retta è l’asse radicale del fascio.

Per l’asse centrale, questo sarà perpendicolare all’asse radicale e dovrà passare per il punto di tangenza {A}.

Riscriviamo l’equazione dell’asse radicale nella forma esplicita, in modo da individuarne il coefficiente angolare {m_t}:

t:y=-x+2 \quad \Rightarrow \quad m_t=-1

Ora, l’asse centrale sarà la retta passante per {A} ed avente coefficiente angolare {-\dfrac{1}{m_t}}. Infatti, se l’asse centrale è perpendicolare all’asse radicale, il coefficiente angolare dell’uno dovrà essere l’inverso del reciproco dell’altro (vedi: perpendicolarità fra rette). Abbiamo:

r_C: y-y_A=-\dfrac{1}{m_t}(x-x_A)

ovvero sostituendo i valori:

r_C:y-1=1\cdot(x-1)

ovvero:

r_C: y=x

Quindi l’asse centrale del fascio è la bisettrice del primo e terzo quadrante.

Torniamo ora a considerare, negli esercizi sui fasci di circonferenze, il caso dei fasci di circonferenze secanti. In particolare, l’esercizio a seguire presenta numerosi quesiti ed è quindi una buona occasione per allenarsi.

Esercizio 3

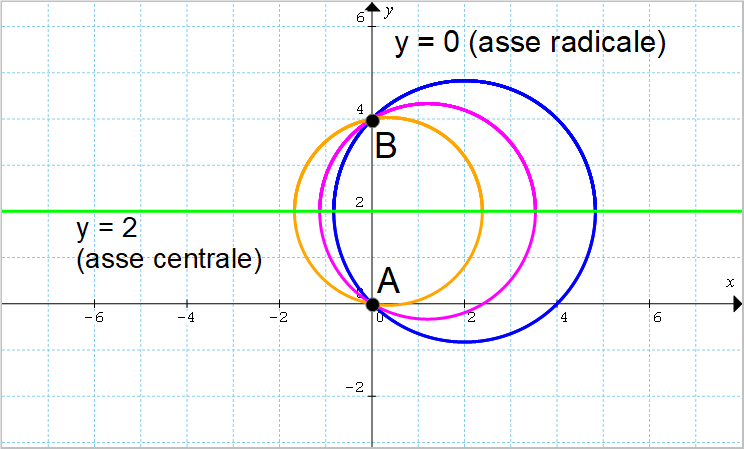
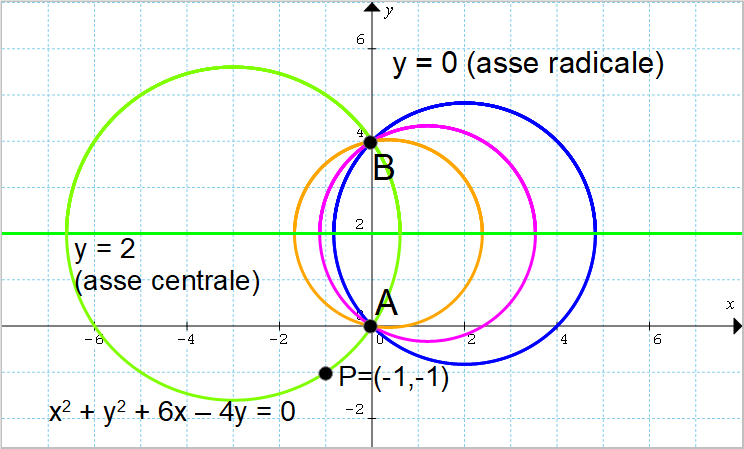
Studiare il fascio di circonferenze di equazione {(1+k)x^2+(1+k)y^2-12x-4(1+k)y=0} quindi determinare il valore di {k} per il quale si ottiene: la circonferenza passante per {P=(-1,-1)}, la circonferenza tangente nell’origine alla retta {r: 3x+2y=0}, la circonferenza che ha il centro sulla retta {s:x+y+4=0} ed infine la circonferenza con raggio {\sqrt{5}}.

Cominciamo con il classificare il fascio. L’equazione data del fascio è:

(1+k)x^2+(1+k)y^2-12x-4(1+k)y=0

In questa forma l’equazione non ci fornisce molte informazioni. Proviamo allora a ricondurre l’equazione alla forma canonica:

x^2+y^2+ax+by+c=0

Tale forma è di nostro interesse poiché offre come sappiamo delle informazioni sul centro della circonferenza.

Nel nostro caso, per {k \neq -1} abbiamo, dividendo tutti i termini per {1+k}:

\dfrac{1+k}{1+k}x^2+\dfrac{1+k}{1+k}y^2-\dfrac{12}{1+k}x-4\dfrac{1+k}{1+k}y=0

ovvero:

x^2+y^2-\dfrac{12}{1+k}x-4y=0

L’equazione del fascio è ora in una forma molto simile all’equazione in forma canonica di una circonferenza.

Come possiamo vedere, il coefficiente del termine in {x}, ovvero il coefficiente {a}, dipende da {k}. Ma poiché l’ascissa del centro della circonferenza dipende dal coefficiente {a}, concludiamo che nel nostro caso il centro delle circonferenze del fascio cambia con il parametro {k}. Di conseguenza, possiamo fin da subito escludere di avere a che fare con un fascio di circonferenze concentriche.

Cerchiamo di ricondurre l’equazione del fascio alla forma {1}, in modo da poter ricavare le equazioni delle sue circonferenze generatrici. L’idea è quella di calcolare i prodotti nell’equazione del fascio di partenza, e quindi, una volta riordinati opportunamente i termini, eseguire un raccoglimento rispetto a {k}:

\begin{align*} &x^2+kx^2+y^2+ky^2-12x-4y-4ky=0; \\ \\ & x^2+y^2-12x-4y+k(x^2+y^2-4y)=0\end{align*}

Le circonferenze generatrici del fascio sono dunque:

\mathscr{C}_1:x^2+y^2-12x-4y=0; \qquad \mathscr{C}_2: x^2+y^2-4y=0

Ricerchiamo gli eventuali punti base del fascio:

\begin{cases} x^2+y^2-12x-4y=0 \\ \\ x^2+y^2-4y=0\end{cases}

Risolvendo come al solito per riduzione:

\small \begin{cases} -12x-\cancel{4y}+\cancel{4y}=0 \quad \rightarrow \quad  \boxed{x = 0} \\ \\ x^2+y^2-4y=0 \quad \rightarrow \: y^2-4y=0 \quad \rightarrow \: y(y-4)=0 \quad \rightarrow y=0 \: \vee \: y=4\end{cases}

Otteniamo così i due punti base:

A=(0,0); \qquad B=(0,4)

Poiché i punti base sono due, ci ritroviamo con un fascio di circonferenze secanti. L’asse radicale ha equazione:

r_{AB}: x = 0

e coincide pertanto con l’asse {y}.

L’asse centrale essendo perpendicolare all’asse radicale sarà in questo caso della forma:

r_C: y=c

e dato che i centri delle circonferenze generatrici hanno entrambi ordinata uguale a {2} (basta osservare le corrispondenti equazioni) abbiamo:

r_C: y= 2

Proseguiamo a questo punto determinando il valore di {k} per il quale si ottiene a partire dall’equazione del fascio la circonferenza passante per il punto {P=(-1, -1)}.

L’idea è quella di riprendere l’equazione del fascio ad esempio nella forma iniziale:

(1+k)x^2+(1+k)y^2-12x-4(1+k)y=0

Questa è per le nostre finalità la forma più comoda, in quanto compare il minor numero di lettere {x} ed {y}, e quindi come vedremo le sostituzioni per le variabili {x} ed {y} risulteranno più rapide.

Ora, possiamo riguardare tale equazione, con lieve abuso di linguaggio, all’equazione della generica circonferenza del fascio. Infatti, l’equazione è praticamente della forma:

Ax^2+Ay^2+Bx+Cy+D=0

ma con coefficienti dipendenti dal parametro {k}.

Ora, se vogliamo verificare che una circonferenza passi per il punto {P}, dobbiamo imporre la relativa condizione di appartenenza. In altre parole, si tratterà di sostituire le coordinate del punto {P} nell’equazione della circonferenza, e quindi verificare che si ottenga un’uguaglianza numerica vera.

Nel caso dell’equazione della generica circonferenza del fascio, i coefficienti che compaiono nell’equazione dipendono dal parametro {k}. Così, l’idea è quella ancora di sostituire alle lettere {x} ed {y} nell’equazione del fascio le coordinate del punto {P}. Tuttavia, così facendo si otterrà un’equazione nella sola incognita {k}. Ma risolvendola, troveremo il valore di {k} che soddisfa la condizione di appartenenza della generica circonferenza del fascio al punto {P}. E quindi in conclusione troveremo il valore di {k} che corrisponde alla circonferenza del fascio passante per {P}.

Procedendo in questo modo abbiamo:

\small \begin{align*} &(1+k)x^2+(1+k)y^2-12x-4(1+k)y=0 \quad \text{con} \quad x=-1, \: y=-1 \\ \\ & \Rightarrow \quad (1+k) \cdot (-1)^2+(1+k)\cdot(-1)^2-12 \cdot (-1)-4\cdot(1+k)\cdot(-1)=0;\\ \\ & 1+k+1+k+12+4+4k=0;\\ \\ & 6k+18=0 \quad \Rightarrow \quad k=-\dfrac{18}{6}=-3\end{align*}

Così a partire dall’equazione del fascio, ponendo {k=-3} otteniamo la circonferenza passante per il punto {P=(-1,-1)}, ovvero la circonferenza di equazione:

\begin{align*} &(1+k)x^2+(1+k)y^2-12x-4(1+k)y=0 \quad \text{con} \quad k=-3 \\ \\ & \Rightarrow \quad (1-3)x^2+(1-3)y^2-12x-4(1-3)y=0; \\ \\ & -2x^2-2y^2-12x-4y+12y=0;\\ \\ & -2x^2-2y^2-12x+8y=0;\\ \\ & x^2+y^2+6x-4y=0\end{align*}

Effettivamente, come verifica, a partire dall’ultima equazione scritta, per {x=-1} ed {y=-1} ritroviamo un’uguaglianza numerica vera:

(-1)^2+(-1)^2+6\cdot(-1)-4 \cdot(-1)=0 \quad \Rightarrow \quad 0 = 0

per cui effettivamente per {k=-3} otteniamo la circonferenza del fascio che passa per {P}.

Ci domandiamo ora per quale valore del parametro {k} otteniamo la circonferenza del fascio tale da essere tangente in corrispondenza dell’origine alla retta:

r: 3x+2y=0

In altre parole, ci chiediamo quale circonferenza del fascio risulti tangente alla retta {r} nel punto {O=(0,0)}. Ora, osserviamo che il punto {O} appartiene alla circonferenza, in quanto coincide con il punto base {A}.

Ricordiamo che se una circonferenza è tangente ad una retta in un suo punto, il centro della circonferenza dovrà necessariamente passare per la retta perpendicolare alla tangente e passante per quello stesso punto. Ciò deriva da quanto visto sulle condizioni per determinare l’equazione di una circonferenza.

Infatti, ricordiamo che una circonferenza è univocamente determinata se è nota l’equazione della retta ad essa tangente in un suo punto e se sono note le coordinate di due punti della circonferenza. In tal caso basta infatti determinare l’equazione dell’asse del segmento avente per estremi i due punti, e quindi ricercare il centro della circonferenza come intersezione tra l’asse del segmento e la perpendicolare alla retta tangente passante per il punto di tangenza.

Da ciò deriva che se una circonferenza è tangente in un suo punto ad una data retta, il centro della circonferenza dovrà necessariamente appartenere alla perpendicolare alla retta tangente passante per quel punto.

Nel nostro caso, dobbiamo ancora ragionare sulla generica circonferenza del fascio, che possiamo vedere come la circonferenza con equazione parametrica:

(1+k)x^2+(1+k)y^2-12x-4(1+k)y=0

ovvero, come abbiamo già visto all’inizio, per {k \neq -1}:

x^2+y^2-\dfrac{12}{1+k}x-4y=0

Così il centro della circonferenza, che nel caso di un’equazione canonica non dipendente dal parametro è:

C=\left( -\dfrac{1}{2}a, -\dfrac{1}{2}b\right)

nel nostro particolare caso diviene:

C=\left( -\dfrac{1}{2} \cdot \left(-\dfrac{12}{1+k}\right), -\dfrac{1}{2} \cdot (-4)\right)

ovvero:

C=\left( \dfrac{6}{1+k}, 2\right)

Ora, noi ricerchiamo la circonferenza del fascio tale che alla perpendicolare alla tangente passante per l’origine appartenga il centro {C} appena scritto. Si tratterà quindi di scrivere l’equazione di tale perpendicolare, e quindi trovare il valore di {k} che verifica la condizione di appartenenza al punto {C}.

L’equazione della retta tangente alla circonferenza è:

r: 3x+2y=0

ovvero in forma esplicita:

r: y=-\dfrac{3}{2}x

da cui {m=-\dfrac{3}{2}}. Ma allora, per la relazione di perpendicolarità fra rette, il coefficiente di una retta perpendicolare ad {r} avrà coefficiente angolare {\dfrac{2}{3}}. E poiché tale perpendicolare deve passare per il punto {C}, ricordando l’equazione di una retta passante per un punto e con coefficiente angolare noto, l’equazione della perpendicolare stessa sarà:

y-y_C=\dfrac{2}{3}(x-x_C)

ovvero:

y-2=\dfrac{2}{3} \left( x-\dfrac{6}{1+k}\right)

Ora, poiché la retta è tangente alla circonferenza nell’origine, sostituendo {x=0} e {y=0} abbiamo:

-2=\dfrac{2}{3} \cdot \left( -\dfrac{6}{1+k}\right)

e quindi:

-\dfrac{12}{3(1+k)}+2=0

ovvero semplificando:

\dfrac{-4}{(1+k)}+2=0

da cui ricavando {k}:

\begin{align*} & \dfrac{-4+2(1+k)}{1+k}=0;\\ \\ & -4+2+2k=0, \quad k \neq -1;\\ \\ & 2k=2 \quad \Rightarrow \quad k=1 \end{align*}

Quindi per {k=1} otteniamo a partire dall’equazione del fascio la circonferenza tangente ad {r} nell’origine, ovvero la circonferenza:

\begin{align*} &(1+k)x^2+(1+k)y^2-12x-4(1+k)y=0 \quad \text{con} \quad k=1 \\ \\ & \Rightarrow  \quad 2x^2+2y^2-12x-8y=0;\\ \\ & \boxed{x^2+y^2-6x-4y=0}\end{align*}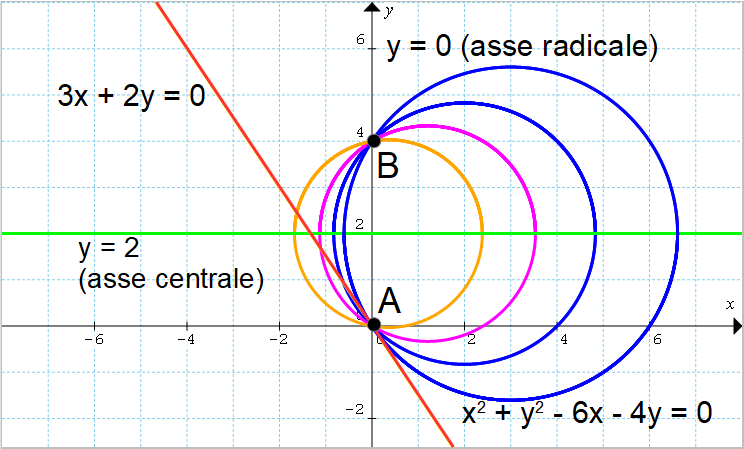

Passiamo al quesito successivo. Ci viene richiesto di determinare il valore di {k} che corrisponde alla circonferenza del fascio avente centro sulla retta {s: x+y+4=0}.

Per trovare il valore del parametro {k} che risponde a tale condizione basta imporre la condizione di appartenenza del centro {C=\left( \dfrac{6}{1+k}, 2\right)} alla retta {s}:

\underbrace{\dfrac{6}{1+k}}_{x_C}+\underbrace{2}_{y_C}+4=0

da cui otteniamo:

\begin{align*} & \dfrac{6+2(1+k)+4(1+k)}{1+k}=0;\\ \\ & 6+2+2k+4+4k=0, \quad k \neq -1; \\ \\ & 6k+12=0 \quad \Rightarrow \quad k=-2\end{align*}

Quindi la circonferenza del fascio che ha centro sulla retta {s} ha equazione:

\begin{align*} &(1+k)x^2+(1+k)y^2-12x-4(1+k)y=0 \quad \text{con} \quad k = -2 \\ \\ & \Rightarrow \quad -x^2-y^2-12x+4y=0; \\ \\ & \boxed{x^2+y^2+12x-4y=0} \end{align*}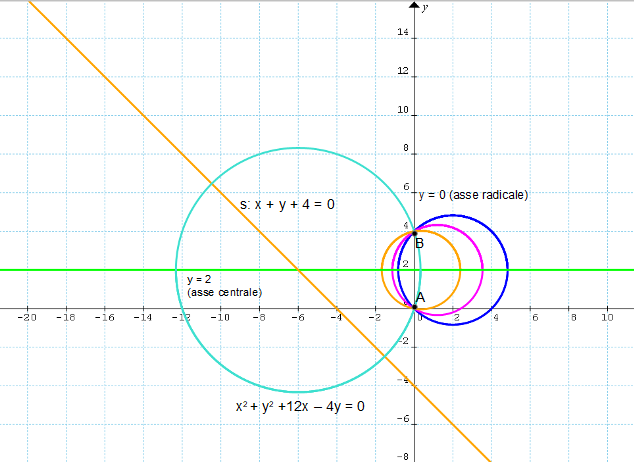

Infine, per rispondere all’ultimo quesito, dobbiamo determinare il valore del parametro {k} al quale corrisponde la circonferenza del fascio avente raggio {\sqrt{5}}. Allo scopo, riprendiamo l’equazione del fascio nella forma precedentemente scritta:

x^2+y^2-\dfrac{12}{1+k}x-4y=0

Come già detto l’equazione pur essendo parametrica è della stessa forma dell’equazione canonica di una circonferenza, con {a=-\dfrac{12}{1+k}}, {b=-4} e {c=0}. Inoltre, come in precedenza scritto per il centro abbiamo:

C=\left( \dfrac{6}{1+k}, 2\right)

Il raggio della circonferenza con equazione in forma canonica è dato da:

r=\sqrt{x_C^2+y_C^2-c}

e quindi nel nostro caso:

\sqrt{5}=\sqrt{\left(\dfrac{6}{1+k}\right)^2+2^2-0}

ovvero:

\sqrt{5}=\sqrt{\dfrac{36}{(1+k)^2}+4}

All’interno della radice abbiamo una somma di quadrati, e quindi una quantità sempre positiva. Inoltre, il raggio {r} per una circonferenza reale non degenere è per definizione sempre positivo. Di conseguenza, possiamo elevare al quadrato entrambi i membri dell’equazione senza alcuna discussione:

(\sqrt{5})^2=\dfrac{36}{(1+k)^2}+4

ovvero, sviluppando i calcoli:

\begin{align*} & 5-\dfrac{36}{1+2k+k^2}-4=0; \\ \\ & \dfrac{5+10k+5k^2-36-4-8k-4k^2}{1+2k+k^2}=0; \\ \\ & k^2+2k-35=0 \\ \\ &k_{1,2}=-1\pm \sqrt{1+35}=-1\pm 6=\begin{cases} 5 \\ \\ -7\end{cases}\end{align*}

Di conseguenza le circonferenze del fascio che hanno raggio {\sqrt{5}} sono quelle che si ottengono per {k=5} e {k=-7}, ovvero le circonferenze di equazioni:

\begin{align*} &(1+k)x^2+(1+k)y^2-12x-4(1+k)y=0 \quad \text{con} \quad k = 5 \\ \\ & \Rightarrow 6x^2+6y^2-12x-4y-20y=0; \\ \\ & 6x^2+6y^2-12x-24y=0;\\ \\ & \boxed{x^2+y^2-2x-4y=0}\end{align*}

\begin{align*} &(1+k)x^2+(1+k)y^2-12x-4(1+k)y=0 \quad \text{con} \quad k = -7 \\ \\ & \Rightarrow \quad -6x^2-6y^2-12x-4y+28y=0;\\ \\ & -6x^2-6y^2-12x+24y=0;\\ \\ & \boxed{x^2+y^2+2x-4y=0}\end{align*}

L’esercizio è così concluso.

Proseguiamo ancora gli esercizi sui fasci di circonferenze esaminando un caso di fascio di circonferenze concentriche, ovvero un fascio dato da circonferenze aventi tutte il medesimo centro.

Esercizio 4

Classificare il fascio di equazione: {x^2+y^2+2x-2y+\dfrac{1-2k}{1+k}=0} e quindi determinare per quale valore di {k} si ottiene l’equazione di una circonferenza tangente alla retta {t:2x-y+4=0}.

E’ immediato notare che siamo in presenza di un fascio di circonferenze concentriche. Infatti, nell’equazione data i termini in {x} ed {y} non dipendono dal parametro. E poiché dai coefficienti di tali termini dipendono le coordinate del centro delle circonferenze del fascio, concludiamo che tutte le circonferenze hanno lo stesso centro.

Ora, richiedere che la generica circonferenza del fascio sia tangente alla retta {t} equivale a richiedere che il sistema contenente l’equazione della generica circonferenza del fascio e l’equazione della retta tangente abbia un’unica soluzione:

\begin{cases} x^2+y^2+2x-2y+\dfrac{1-2k}{1+k}=0 \\ \\  2x-y+4=0\end{cases}

Ma ciò equivale a richiedere che l’equazione risolvente il sistema abbia determinante nullo. Di conseguenza, basterà imporre la condizione di determinante dell’equazione risolvente nullo e quindi calcolare il corrispondente valore del parametro {k}.

Come al solito, esplicitiamo una delle due variabili dall’equazione della retta, ad esempio la variabile {x}:

\begin{cases} x^2+y^2+2x-2y+\dfrac{1-2k}{1+k}=0 \\ \\x=\dfrac{y-4}{2}\end{cases}

Sostituendo l’espressione appena ottenuta nella prima equazione otteniamo l’equazione risolvente il sistema, che scriviamo separatamente:

\begin{align*} &\left( \dfrac{y-4}{2}\right)^2+y^2+2 \left( \dfrac{y-4}{2}\right)-2y+\dfrac{1-2k}{1+k}=0\end{align*}

Eseguendo i calcoli ci ritroviamo con la seguente equazione nell’incognita {y} e contenente il parametro {k}:

\scriptsize\begin{align*} &\dfrac{y^2-8y+16}{4}+y^2+y-4-2y+\dfrac{1-2k}{1+k} = 0; \\ \\ & \dfrac{(1+k)(y^2-8y+16)+4(1+k)y^2+4(1+k)y-16(1+k)-8(1+k)y+4-8k}{4(1+k)}=0;\\ \\ & \dfrac{y^2-8y+16+ky^2-8ky+16k+4y^2+4ky^2+4y+4ky-16-16k-8y-8ky+4-8k}{4(1+k)}=0;\\ \\ & (1+k+4+4k)y^2+(-8-8k+4+4k-8-8k)y+16+16k-16-16k+4-8k=0, \quad k \neq-1;\\ \\ &(5+5k)y^2+(-12k-12)y+(-8k+4)=0 \end{align*}

Abbiamo così un’equazione di secondo grado in forma normale con coefficienti dipendenti dal parametro {k}:

a=5+5k; \quad b=-12k-12; \quad c=-8k+4

Imponiamo il determinante dell’equazione uguale a zero. Utilizziamo per brevità la formula del Delta/4:

\begin{align*} & \left( \dfrac{b}{2}\right)^2-ac=0; \\ \\ & (-6k-6)^2-(5+5k)\cdot(-8k+4)=0; \\ \\ & 36k^2+72k+36+40k-20+40k^2-20k=0;\\ \\ & 76k^2+92k+16=0; \\ \\ & 19k^2+23k+4=0\end{align*}

Otteniamo per {k}:

\begin{align*} &k_{1,2}=\dfrac{-23\pm \sqrt{23^2-4 \cdot19 \cdot 4}}{38}= \dfrac{-23 \pm \sqrt{529-304}}{38}=\\ \\ & =\dfrac{-23 \pm \sqrt{225}}{38}=\dfrac{-23 \pm 15}{38}=\begin{cases} -\dfrac{8}{38}=-\dfrac{4}{19} \\ \\ -\dfrac{38}{38}=-1\end{cases}\end{align*}

Prestiamo ora attenzione al fatto che il valore {-1} non è accettabile per {k}. Infatti nello svolgere i precedenti calcoli avevamo imposto la condizione {k \neq -1}. Così otteniamo per {k} il solo valore:

k=-\dfrac{4}{19}

al quale corrisponde la circonferenza del fascio tale da essere tangente alla retta {t}:

\begin{align*} &x^2+y^2+2x-2y+\dfrac{1-2k}{1+k}=0 \qquad \text{con} \quad k=-\dfrac{4}{19} \\ \\ & \Rightarrow \: x^2+y^2+2x-2y+\dfrac{1+\dfrac{8}{19}}{1-\dfrac{4}{19}}=0;\\ \\ & \boxed{\mathscr{C}': x^2+y^2+2x-2y+\dfrac{9}{5}=0}\end{align*}

Veniamo ora all’ultimo esercizio, nel quale affronteremo un ultimo caso, relativo ad un fascio di circonferenze non concentriche e prive di punti in comune.

Esercizio 5

Dato il fascio di circonferenze di equazione {x^2+y^2-2kx+(k+1)y-2k=0} determinare per quale valore di {k} si ottiene la circonferenza tale da staccare sulla retta {y=x} una corda di lunghezza uguale a {\dfrac{1}{2}\sqrt{66}}. Inoltre, classificare il fascio.

In questo esercizio vediamo come determinare la circonferenza del fascio che stacca su una data retta una corda di lunghezza assegnata. In questo modo ampliamo quanto visto sugli esercizi sui fasci di circonferenze precedenti.

Ricordiamo che dati due punti appartenenti ad una circonferenza, la corda costruita su quei due punti è il segmento che unisce i due punti stessi. Inoltre, la lunghezza della corda è uguale alla distanza tra i due punti considerati.

Nel nostro caso, dobbiamo individuare la circonferenza del fascio tale da staccare sulla retta {y=x} una corda di lunghezza {\dfrac{1}{2}\sqrt{66}}. In altre parole, richiediamo che la circonferenza intersechi la retta in due punti, e che la distanza tra i due punti sia uguale a {\dfrac{1}{2}\sqrt{66}}. Se indichiamo tali punti con {P_1} e {P_2} abbiamo orientativamente la seguente situazione:

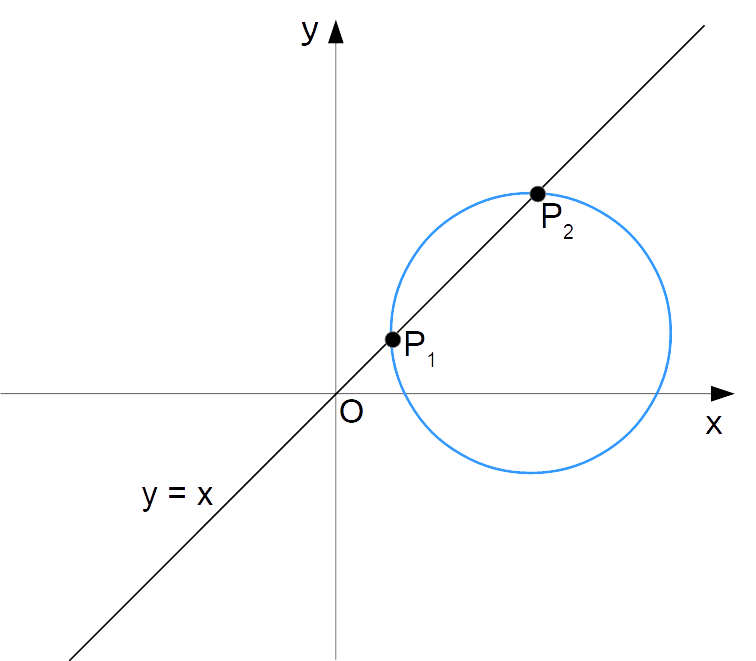
La distanza tra i due punti {P_1} e {P_2} è uguale alla lunghezza della corda {\overline{P_1P_2}}. Così intanto dobbiamo imporre:

\overline{P_1P_2}=\dfrac{1}{2}\sqrt{66}

Consideriamo ora l’equazione del fascio:

x^2+y^2-2kx+(k+1)y-2k=0

L’idea è quella di determinare gli eventuali punti di intersezione della generica circonferenza del fascio (la cui equazione corrisponde a quella appena scritta) con la retta {y=x}. Di conseguenza dovremo impostare il sistema:

\begin{cases} x^2+y^2-2kx+(k+1)y-2k=0 \\ \\ y=x\end{cases}

Procedendo per sostituzione otteniamo l’equazione risolvente:

x^2+x^2-2kx+(k+1)x-2k=0

ovvero:

2x^2+(-k+1)x-2k=0

per la quale otteniamo come soluzioni le seguenti espressioni per la variabile {x} in funzione di {k}:

\begin{align*} &x_{1,2}= \dfrac{k-1\pm \sqrt{(-k+1)^2-4 \cdot 2 \cdot (-2k)}}{4}=\\ \\ & =\dfrac{k-1 \pm \sqrt{k^2-2k+1+16k}}{4}=\dfrac{k-1\pm \sqrt{k^2+14k+1}}{4}=\\ \\ & =\begin{cases} \dfrac{k-1+\sqrt{k^2+14k+1}}{4} \\ \\ \dfrac{k-1-\sqrt{k^2+14k+1}}{4}\end{cases}\end{align*}

Da ciò otteniamo i seguenti punti di intersezione fra la retta e la circonferenza, in funzione di {k}:

\small \begin{align*} &P_1=(x_1, y_1)=(x_1, x_1)=\left(\dfrac{k-1+\sqrt{k^2+14k+1}}{4}, \dfrac{k-1+\sqrt{k^2+14k+1}}{4} \right)\end{align*}

\small \begin{align*} &P_2=(x_2, y_2)=(x_2, x_2)=\left(\dfrac{k-1-\sqrt{k^2+14k+1}}{4}, \dfrac{k-1-\sqrt{k^2+14k+1}}{4} \right)\end{align*}

Infatti poiché a sistema abbiamo l’equazione {y=x} le ascisse e le ordinate di ciascun punto di intersezione tra retta e circonferenza sono tra loro uguali.

Ora, la lunghezza della corda staccata dalla retta {y=x} sulla generica circonferenza del fascio sarà uguale alla distanza tra i due punti {P_1} e {P_2} (vedi distanza tra due punti nel piano):

\begin{align*} &\overline{P_1P_2}=\sqrt{(x_{P_2}-x_{P_1})^2+(y_{P_2}-y_{P_1})^2}=\\ \\ & =\tiny{\sqrt{\left( \dfrac{k-1-\sqrt{k^2+14k+1}}{4}-\dfrac{k-1+\sqrt{k^2+14k+1}}{4}\right)^2+\left( \dfrac{k-1-\sqrt{k^2+14k+1}}{4}-\dfrac{k-1+\sqrt{k^2+14k+1}}{4}\right)^2}}=\end{align*}

Proseguendo i passaggi:

\scriptsize\begin{align*} & =\sqrt{\left(\dfrac{k-1-k+1-2\sqrt{k^2+14k+1}}{4}\right)^2+\left( \dfrac{k-1-k+1-2\sqrt{k^2-14k+1}}{4}\right)^2}= \\ \\ & =\sqrt{\left( \dfrac{-2\sqrt{k^2+14k+1}}{4}\right)^2+\left( \dfrac{-2\sqrt{k^2-14k+1}}{4}\right)^2}=\\ \\ & =\sqrt{\dfrac{k^2+14k+1}{4}+\dfrac{k^2+14k+1}{4}}=\boxed{\dfrac{\sqrt{2k^2+28k+2}}{2}}\end{align*}

Abbiamo così determinato un’espressione per la lunghezza della corda staccata dalla circonferenza generica del fascio sulla retta {y=x}. Ora imponiamo che tale lunghezza sia uguale alla quantità indicata nel testo, ovvero {\dfrac{1}{2}\sqrt{66}}:

\begin{align*} &\dfrac{\sqrt{2k^2+28k+2}}{2}=\dfrac{1}{2}\sqrt{66}\end{align*}

ovvero:

\sqrt{2k^2+28k+2}=\sqrt{66}

Ora, per risolvere l‘equazione irrazionale, teniamo conto che il secondo membro, in quanto radice con indice pari, è una quantità sempre positiva. Per cui non serve alcuna condizione di concordanza dei segni. Tuttavia, dobbiamo imporre la condizione di realtà del radicale al primo membro, ritrovandoci con una disequazione di secondo grado:

2k^2+28k+2 \geq 0

Risolviamo l’equazione di secondo grado associata:

2k^2+28k+2 = 0

ovvero:

k^2+14k+1=0

Otteniamo le soluzioni:

k_{1,2} ={-7 \pm \sqrt{(7)^2-1}}{}=-7 \pm \sqrt{48}=-7 \pm 4\sqrt{3}=\begin{cases} -7+4\sqrt{3} \\ \\ -7-4\sqrt{3}\end{cases}

La disequazione è verificata per valori esterni agli zeri, compresi gli zeri, ovvero:

k \leq -7-4\sqrt{3}\quad \vee \quad   k \geq -7 + 4\sqrt{3}

A questo punto, tornando all’equazione irrazionale, possiamo elevare entrambi i membri al quadrato, verificando poi che le soluzioni che otterremo soddisfino la condizione di realtà appena scritta. Abbiamo:

\begin{align*} &\left(\sqrt{2k^2+28k+2}\right)^2=\left(\sqrt{66}\right)^2;\\ \\ & 2k^2+28k+2-66=0;\\ \\ & 2k^2+28k-64=0;\\ \\ & k^2+14k-32=0\end{align*}

Risolvendo l’equazione di secondo grado appena scritta otteniamo:

\begin{align*} &k_{1,2}=-7 \pm\sqrt{7^2+32}=-7 \pm \sqrt{49+32}=-7\pm \sqrt{81}=\\ \\ & =-7\pm 9=\begin{cases} 2 \\ \\ -16\end{cases}  \end{align*}

Entrambi i valori sono accettabili poiché rispettano la condizione di realtà del radicale dell’equazione irrazionale.

Otteniamo così i valori {k=2} e {k=-16}, ai quali corrispondono non soltanto una ma due circonferenze del fascio tali da staccare sulla retta {y=x} una corda di lunghezza {\dfrac{1}{2}\sqrt{66}}.

A partire dall’equazione del fascio:

x^2+y^2-2kx+(k+1)y-2k=0

le equazioni di tali circonferenze sono, sostituendo i valori di {k} appena trovati:

\small \mathscr{C}'=x^2+y^2-4x+3y-4=0; \qquad \mathscr{C}''=x^2+y^2+32x-15y+32=0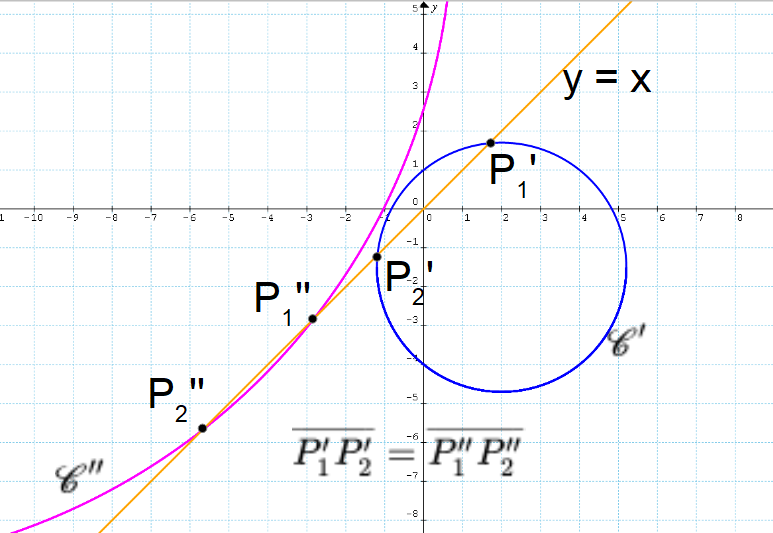

Infine, per classificare il fascio riprendiamo l’equazione del fascio stesso di partenza:

x^2+y^2-2kx+(k+1)y-2k=0

Come visto nei precedenti esercizi sui fasci di circonferenze, riconduciamo l’equazione del fascio ad altra forma, ad esempio:

\begin{align*} &x^2+y^2-2kx+ky+y-2k=0;\\ \\ & x^2+y^2+y-2kx+ky-2k=0;\\ \\ & x^2+y^2+y+k(-2x+y-2)=0\end{align*}

Il fascio ha dunque una circonferenza generatrice di equazione:

\mathscr{C}_1:x^2+y^2+y=0

e l’asse radicale di equazione:

r:-2x+y-2=0

Determiniamo i punti base come intersezione della circonferenza {\mathscr{C}_1} e dell’asse radicale:

\begin{cases}x^2+y^2+y=0 \\ \\ -2x+y-2=0 \end{cases}

Risolviamo il sistema per sostituzione:

\small \begin{cases} x^2+(2x+2)^2+2x+2=0 \quad \rightarrow \:x^2+4x^2+8x+4+2x+2=0 \\ \\ y=2x+2\end{cases}

E quindi:

\begin{cases} 5x^2+10x+6=0  \\ \\ y=2x+2\end{cases}

Tuttavia, la prima equazione a sistema non ammette soluzioni reali. Allora, il sistema è impossibile e non esistono punti di intersezione fra la circonferenza generatrice e l’asse radicale. Di conseguenza, il fascio di circonferenze è privo di punti base. Quindi non siamo di fronte a un fascio di circonferenze secanti e nemmeno ad un fascio di circonferenze tangenti.

Inoltre, nell’equazione del fascio i coefficienti dei termini in {x} e {y} dipendono dal parametro {k}, per cui non ci ritroviamo nemmeno nel caso di un fascio di circonferenze concentriche. Abbiamo quindi un fascio di circonferenze non concentriche e prive di punti in comune.

Conclusioni

Per quanto riguarda questa scheda di esercizi sui fasci di circonferenze è tutto.

Abbiamo visto che per classificare un fascio di circonferenze basta lavorare sull’equazione corrispondente, in modo da individuare le circonferenze generatrici, oppure una circonferenza generatrice e l’asse radicale. L’intersezione delle rispettive equazioni fornirà gli eventuali punti base del fascio. Se i punti base sono due, le circonferenze del fascio sono secanti, se il punto base è invece soltanto uno, le circonferenze del fascio sono tutte tangenti ad una stessa retta nel medesimo punto.

Nel caso in cui non si abbiano punti base, il fascio di circonferenze può essere dato da circonferenze concentriche, oppure da circonferenze non concentriche e prive di punti in comune. Per distinguere tra questi due ultimi casi, basta riscrivere l’equazione del fascio in una forma simile a quella dell’equazione di una circonferenza in forma canonica (se non è già in tale forma), e quindi controllare se i coefficienti dei termini in {x} e {y} dipendono o no dal parametro. Se si ha tale dipendenza, le circonferenze del fascio sono concentriche. Diversamente, queste sono non concentriche e prive di punti di intersezione.

In particolare, volendo fornire uno schema generale per gli esercizi sui fasci di circonferenze, se il fascio ha un’equazione del tipo:

\small(1+k)x^2+(1+k)y^2+(a_1+ka_2)x+(b_1+kb_2)y+c_1+kc_2=0, \quad k \neq -1

per ricondurlo ad una forma simile all’equazione in forma canonica di una circonferenza, dobbiamo dividere tutti i termini per {1+k} (vedi l’esercizio 3). In tal modo, come richiesto dall’equazione in forma canonica di una circonferenza, ci ritroviamo con i coefficienti dei termini in {x^2} ed {y^2} unitari:

x^2+y^2+\dfrac{a_1+ka_2}{1+k}x+\dfrac{b_1+kb_2}{1+k}y+\dfrac{c_1+kc_2}{1+k}=0

Per stabilire se le circonferenze del fascio sono concentriche oppure no, una volta ricondotta l’equazione del fascio a questa forma, basta controllare se i coefficienti dei termini in {x} e {y} dipendono dal parametro {k} oppure no.

Osserviamo che per stabilire se le coordinate del centro delle circonferenze del fascio dipendono o meno dal parametro occorre necessariamente ricondurre l’equazione del fascio alla forma appena scritta. Ad esempio, consideriamo il fascio di equazione:

(1+k)x^2+(1+k)y^2+(2+2k)x+(2+2k)y-7+k=0

I termini in {x} e {y} dipendono dal parametro {k}, tuttavia siamo in presenza di un fascio di circonferenze concentriche. Per verificarlo, dividiamo tutti i termini per {k}, in modo da ricondurre l’equazione del fascio ad una forma simile a quella dell’equazione della circonferenza in forma canonica:

x^2+y^2+\dfrac{2+2k}{1+k}x+\dfrac{2+2k}{1+k}y+\dfrac{-7+k}{1+k}=0

ovvero:

\begin{align*} &x^2+y^2+\dfrac{2(1+k)}{1+k}x+\dfrac{2(1+k)}{1+k}y+\dfrac{-7+k}{1+k}=0; \\ \\ & x^2+y^2+2x+2y+\dfrac{-7+k}{1+k}=0\end{align*}

Come possiamo vedere, i coefficienti dei termini in {x} e {y} ora non dipendono dal parametro {k}, per cui il fascio di circonferenze dato è un fascio di circonferenze concentriche.

Quello appena riassunto è lo schema da seguire negli esercizi sui fasci di circonferenze per poter riconoscere il tipo di fascio con il quale abbiamo a che fare. In altre parole, quella appena ricordata è la procedura che mostra come classificare un fascio di circonferenze.

Per gli esercizi sui fasci di circonferenze di questa scheda è davvero tutto. Un saluto a tutti voi e buon proseguimento con SìMatematica.