Rette condotte da un punto tangenti a una circonferenza

 - 

Domande e risposte

Come si determinano le equazioni delle rette condotte da un punto esterno tangenti a una circonferenza? Quali metodi è possibile utilizzare?

Per determinare le equazioni delle rette condotte da un punto esterno a una circonferenza e tangenti alla circonferenza stessa esistono principalmente due metodi:

• utilizzo della formula della distanza punto-retta, imponendo che la distanza tra ciascuna retta tangente e il centro della circonferenza sia uguale al raggio;
• scrivere il sistema per ricercare i punti di intersezione tra la circonferenza e ciascuna retta tangente, imponendo che il determinante dell’equazione risolvente sia nullo. In tal modo, è possibile ricavare i coefficienti angolari corrispondenti alle rette tangenti.

Ciascun metodo presenta vantaggi e svantaggi. Il primo metodo offre dei calcoli più leggeri ma richiede più ragionamenti dal punto di vista della geometria. Il secondo metodo, per contro, è molto più meccanico e quindi di applicazione più diretta, ma richiede calcoli più pesanti.

Vediamo in azione entrambi i metodi, risolvendo un problema pratico.

Determinare le equazioni delle rette tangenti a una circonferenza, in particolare la circonferenza {\mathscr{C}_1} di equazione {x^2+y^2-4x-4y-8=0}, condotte per il punto {P=(-2, 4)} esterno alla circonferenza stessa.

Metodo della formula distanza punto-retta. Cominciamo disegnando la circonferenza nel piano cartesiano, il punto {P} ad essa esterno ed infine le rette tangenti alla circonferenza e condotte per il punto esterno stesso.

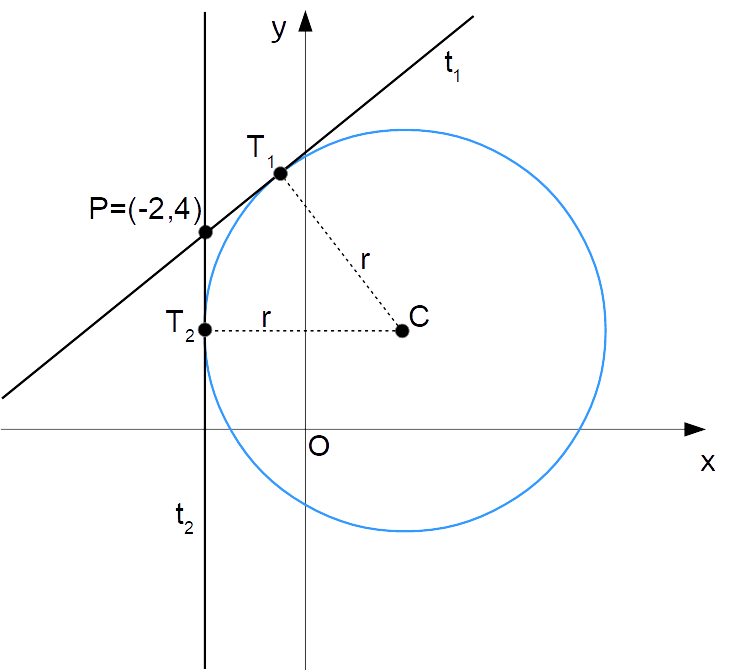
Il nostro obiettivo è determinare le equazioni delle rette {t_1} e {t_2} tangenti alla circonferenze e condotte per il punto {P}.

Indichiamo con {x_P} ed {y_P} rispettivamente l’ascissa e l’ordinata del punto {P}, i cui valori sono comunque noti. Osserviamo che ciascuna delle rette tangenti alla circonferenza ha equazione esprimibile in generale nella forma:

t: y-y_P=m_t(x-x_P)

ove {m_t} rappresenta ciascuno dei valori dei coefficienti angolari delle rette tangenti alla circonferenza. L’equazione appena scritta corrisponde ad un fascio di rette, al variare di {m_t} nei reali.

Riesprimendo tale equazione in forma implicita si ha:

t:m_tx-y-m_tx_P+y_P=0 

ovvero, sostituendo i valori delle coordinate del punto {P}:

t:m_tx-y+2m_t+4=0 \qquad (*)

L’equazione è ora della forma {ax+by+c=0} con {a=m_t, b=-1} e {c=2m_t+4}

Osserviamo che il coefficiente angolare è incognito. Ciò che dobbiamo fare è quindi determinare i due valori di {m_t}, ove possibile, corrispondenti ciascuno ad una delle rette tangenti {t_1} e {t_2}.

Con riferimento alla figura precedente, è chiaro che entrambe le rette tangenti dovranno soddisfare le uguaglianze:

d(t_1,C)=r; \qquad d(t_2, C)=r

ovvero ciascuna distanza tra la retta tangente e il centro {C} dovrà essere uguale alla misura del raggio della circonferenza.

Riscriviamo per comodità l’equazione della circonferenza:

\mathscr{C}_1: x^2+y^2-4x-4y-8=0

Il centro della circonferenza ha coordinate:

x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot (-4)=2; \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot (-4)=2

e quindi abbiamo {C=(2,2)}.

Il raggio {r} della circonferenza è invece dato da:

r=\sqrt{x_C^2+y_C^2-c}=\sqrt{2^2+2^2+8}=4

Così, tenendo conto della forma * con la quale è possibile esprimere ciascuna equazione delle rette tangenti {t_1} e {t_2}, e ricordando la formula della distanza punto-retta, si ha:

\dfrac{|mt \cdot x_C-1 \cdot y_C-2m_t+4|}{\sqrt{m_t^2+1}}=r

e quindi sostituendo i valori delle coordinate del centro {C} e della misura del raggio {r}:

\dfrac{|2m_t-2+2m_t+4|}{\sqrt{m_t^2+1}}=4

ovvero, svolgendo i calcoli:

\begin{align*} & \dfrac{|4m_t+2|}{\sqrt{m_t^2+1}}=4; \\ \\ &\dfrac{|4m_t+2|}{\sqrt{m_t^2+1}}-4=0;\\ \\ & \dfrac{|4m_t+2|-4\sqrt{m_t^2+1}}{\sqrt{m_t^2+1}}=0;\\ \\ & 2\sqrt{m_t^2+1}=|2m_t+1|; \\ \\ & \left[2\sqrt{m_t^2+1}\right]^2=(2m_t+1)^2; \\ \\ &4(m_t^2+1)=4m_t^2+4m_t+1; \\ \\ & \cancel{4m_t^2}+4-\cancel{4m_t^2}-4m_t-1=0 \quad \rightarrow \quad m_t=\dfrac{3}{4}\end{align*}

In sintesi, nei precedenti passaggi abbiamo inizialmente portato tutti i termini al primo membro e li abbiamo ridotti a denominatore comune. Abbiamo poi eliminato il denominatore senza alcuna discussione poiché la quantità {\sqrt{m^2+1}} non si annulla mai (somma di quadrati all’interno della radice). Infine, abbiamo trasportato al secondo membro le quantità non contenenti una radice ed abbiamo elevato al quadrato entrambi i membri. Anche in questo caso, non è necessaria alcuna discussione poiché entrambi i membri sono positivi (radice di indice pari al primo membro, valore assoluto al secondo), ed inoltre il radicale al primo membro è definito in tutti i reali. Per maggiori dettagli vedi la lezione: tangenti ad una circonferenza per un punto esterno.

Abbiamo così ottenuto un solo valore del coefficiente angolare, {m_t=\dfrac{3}{4}}, corrispondente alla retta tangente {t_1} in figura. Di conseguenza, per questa a partire dalla (*), sostituendo il valore per {m_t} appena calcolato, otteniamo l’equazione:

t_1: \dfrac{3}{4}x-y+ \dfrac{3}{2}+4=0 \quad \Rightarrow \quad t_1: \dfrac{3}{4}x-y+\dfrac{11}{2}=0

Tuttavia, non dimentichiamo mai che le rette tangenti ad una circonferenza condotte per un punto ad essa esterno sono sempre due. Ma allora, per quale motivo abbiamo ottenuto un solo valore del coefficiente angolare {m_t}?

In questo caso, abbiamo ottenuto un solo valore del coefficiente angolare {m_t} poiché la retta tangente {t_2}, come mostra la figura, è verticale. E come sappiamo dalle lezioni sulla retta, il coefficiente angolare di una retta verticale non è definito.

Tuttavia, per scrivere l’equazione della retta {t_2} basta osservare che la retta passa per il punto {P}, ed inoltre che una retta verticale ha in generale equazione:

x=c, \qquad c \in \R

Così nel nostro caso avremo:

t_2:x=-2

poiché questa è l’unica retta verticale tale da passare per il punto {P}, il quale ha ascissa uguale al secondo membro dell’equazione appena scritta.

Abbiamo così determinato le equazioni delle due rette tangenti cercate.

Vediamo ora l’utilizzo del metodo alternativo.

Metodo del determinante nullo dell’equazione risolvente. Poiché ciascuna retta tangente ha evidentemente un punto di contatto con la circonferenza, il seguente sistema dovrà risultare determinato:

\begin{cases} \mathscr{C}_1: x^2+y^2-4x-4y-8=0 \\ \\   t: y-y_P=m_t(x-x_P)\end{cases}

Infatti tale sistema corrisponde alla ricerca dei punti di intersezione tra la circonferenza e una delle due rette tangenti alla circonferenza e passanti per il punto esterno {P}.

Ora, riprendiamo l’equazione *:

t:m_tx-y+2m_t+4=0

Riscriviamola in forma esplicita:

y=m_tx+2m_t+4

Così utilizzando l’equazione appena scritta il precedente sistema diviene:

\begin{cases} x^2+y^2-4x-4y-8=0 \\ \\   y=m_tx+2m_t+4\end{cases}

Impostiamo la risoluzione del sistema per sostituzione, in modo da ricavare l’equazione risolvente del sistema. In particolare, sostituiamo a ciascuna lettera {y} nella prima equazione l’espressione fornita dalla seconda equazione, come segue:

\begin{cases} x^2+(m_tx+2m_t+4)^2-4x-4(m_tx+2m_t+4)-8=0 \\ \\ y=m_tx+2m_t+4\end{cases}

Considerando la sola prima equazione abbiamo, ricordando la regola del quadrato di un trinomio:

\begin{align*} &x^2+m_t^2x^2+4m_t^2+\cancel{16}+4m_t^2x+8m_tx+16m_t-4x-4m_tx-8m_t-\cancel{16}-8=0; \\ \\ &(1+m_t^2)x^2+(4m_t^2+8m_t-4-4m_t)x+4m_t^2+16m_t-8m_t-8=0;\\ \\ & (1+m_t^2)x^2+(4m_t^2+4m_t-4)x+4m_t^2+8m_t-8=0 \end{align*}

Quella ottenuta è l’equazione risolvente del sistema (equazione di secondo grado). Ora, l’equazione è della forma {ax^2+bx+c} con {a=1+m_t^2, b=4m_t^2+4m_t-4} e {c=4m_t^2+8m_t-8}. Imponiamo la condizione di determinante dell’equazione risolvente nullo:

\begin{align*} &\left( \dfrac{b}{2}\right)^2-ac=0;\\ \\ & \left( 2m_t^2+2m_t-2\right)^2-(1+m_t^2)(4m_t^2+8m_t-8)=0;\\ \\ & \cancel{4m_t^4}+\cancel{4m_t^2}+4+\cancel{8m_t^3}-\cancel{8m_t^2}-8m_t-\cancel{4m_t^2}-8m_t+8-\cancel{4m_t^4}-\cancel{8m_t^3}+\cancel{8m_t^2}=0;\\ \\ &-16m_t+12=0 \quad \rightarrow \quad m_t=\dfrac{3}{4}\end{align*}

Ritroviamo così anche con il metodo appena utilizzato il valore di {m_t} ottenuto in precedenza, al quale corrisponde la stessa equazione già determinata per la retta tangente {t_1}.

Anche in questo caso, rimane a noi determinare l’equazione della seconda retta tangente condotta per {P}, utilizzando gli stessi ragionamenti visti nello svolgimento precedente.

Abbiamo qui fornito una risposta sintetica relativa alla domanda sul come determinare le rette condotte da un punto e tangenti ad una circonferenza, nel caso di un punto esterno alla circonferenza stessa. Per delle spiegazioni più approfondite rimandiamo alla lezione sulle rette tangenti ad una circonferenza passanti per un punto esterno.

Un saluto a tutti voi e, come sempre, buono studio con SìMatematica!