Parabola con asse obliquo

 - 

Parabola (scuole superiori)

In questa lezione vogliamo mostrare come ottenere l’equazione di una parabola con direttrice data da una retta qualsiasi, ovvero di una parabola con asse di simmetria anche obliquo. Il procedimento che adotteremo si basa sulle conoscenze sin qui acquisite nell’ambito delle lezioni di geometria analitica (retta nel piano e circonferenza). Non proporremo quindi il metodo migliore o più rapido, ma ci baseremo sulle formule della distanza punto-retta e della distanza tra due punti del piano.

La parabola con asse di simmetria obliquo non è argomento delle scuole superiori, ed a livello universitario viene trattata ricorrendo a strumenti matematici più sofisticati rispetto a quelli che qui utilizzeremo. Tuttavia, l’idea è quella di mostrare come sia possibile risolvere il problema anche con strumenti piuttosto semplici. In ogni caso, lo sottolineiamo ancora, l’argomento a livello delle scuole superiori non viene di solito trattato, e di conseguenza la presente lezione può essere considerata al più un utile approfondimento.

Chiariamo che se una parabola ha direttrice qualsiasi, allora la parabola stessa avrà un asse di simmetria avente pendenza qualsiasi (quindi anche obliquo). Infatti, come sappiamo l’asse di simmetria di una parabola è perpendicolare alla sua direttrice. Di conseguenza, il nostro obiettivo sarà scrivere l’equazione di una parabola il cui asse di simmetria forma un angolo di ampiezza arbitraria rispetto all’orizzontale.

Equazione di una parabola con asse di simmetria anche obliquo (direttrice qualsiasi)

Ricordiamo che la parabola è il luogo geometrico dei punti equidistanti da una retta s detta direttrice e da un punto F non appartenente a s detto fuoco. Nel definire la parabola, pertanto, intervengono le nozioni di distanza tra due punti e di distanza tra un punto e una retta. E in particolare, nel caso di parabola con direttrice qualsiasi (asse di simmetria anche obliquo) dovremo utilizzare la formula della distanza punto-retta.

Ora, scegliamo una retta {s} avente equazione:

s: a_sx+b_sy+c_s=0

Questa sarà la direttrice della parabola.

Scegliamo inoltre un punto {F=(x_F, y_F)} non appartenente a {s}, (il fuoco della parabola). Rappresentiamo la direttrice e il fuoco nel piano cartesiano:

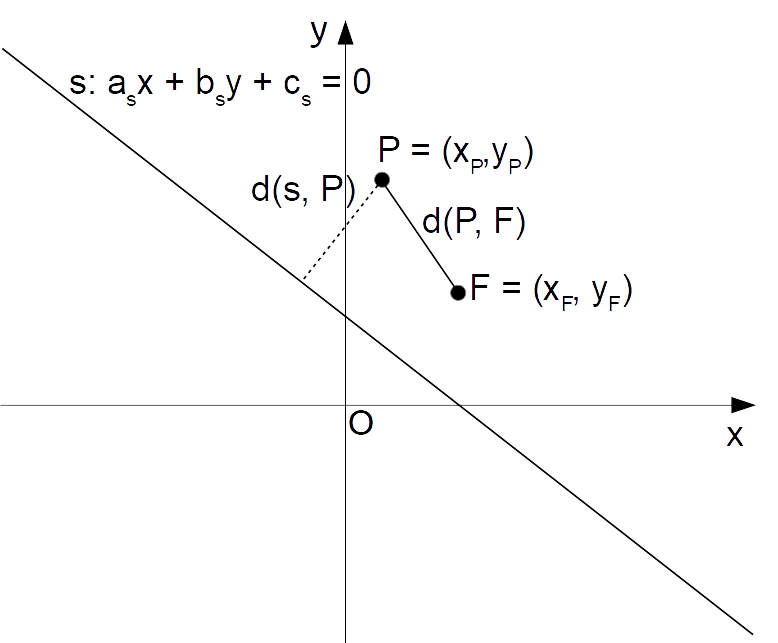
Indichiamo inoltre con {P=(x_P,y_P)} un generico punto della parabola.

Affinché il punto {P} appartenga alla parabola, per la definizione data come luogo geometrico dovrà essere:

d(s,P)=d(P,F)

ovvero, la distanza fra il punto {P} e la retta {s} (direttrice della parabola) deve essere uguale alla distanza fra lo stesso punto {P} e il fuoco {F}.

A questo punto dobbiamo ricordare la definizione di distanza tra una retta e un punto nel piano e la definizione di distanza tra due punti nel piano. La precedente uguaglianza diviene allora:

\dfrac{|a_sx_P+b_sy_P+c_s|}{\sqrt{a_s^2+b_s^2}}=\sqrt{(x_F-x_P)^2+(y_F-y_P)^2}

Osserviamo che qui è già possibile elevare entrambi i membri al quadrato, in modo da liberarci delle radici, tuttavia scegliamo di farlo in un momento successivo. La scelta, ovviamente, non è obbligata.

Portiamo tutti i termini al primo membro e riduciamoli a denominatore comune:

\begin{align*} &\dfrac{|a_sx_P+b_sy_P+c_s|}{\sqrt{a_s^2+b_s^2}}-\sqrt{(x_F-x_P)^2+(y_F-y_P)^2}=0; \\ \\ & \dfrac{|a_sx_P+b_sy_P+c_s|-\sqrt{(a_s^2+b_s^2) \cdot \left( x_F^2-2x_Fx_P+x_P^2+y_F^2-2y_Fy_P+y_P^2\right)}}{\sqrt{a^2_s+b^2_s}}=0\end{align*}

Osserviamo che nel secondo passaggio abbiamo sviluppato i quadrati sotto radice. Inoltre, ci siamo avvalsi della regola del prodotto di radicali con lo stesso indice.

A questo punto, possiamo direttamente eliminare il denominatore senza alcuna condizione. Infatti, il radicando è sempre positivo e non è mai nullo (poiché relativi ad una retta, i coefficienti {a_s} e {b_s} non possono essere entrambi nulli). Così proseguendo i passaggi:

\begin{align*} & |a_sx_P+b_sy_P+c_s|=\\ \\ & =\scriptsize{\sqrt{a_s^2x_F^2-2a_s^2x_Fx_P+a_s^2x_P^2+a_s^2y_F^2-2a_s^2y_Fy_P+a_s^2y_P^2+b_s^2x_F^2-2b_s^2x_Fx_P+b_s^2x_P^2+b_s^2y_F^2-2b_s^2y_Fy_P+b_s^2y_P^2}}; \end{align*}

Ora procediamo elevando al quadrato entrambi i membri dell’equazione. Osserviamo che per fare ciò non è necessaria alcuna discussione. Infatti, il primo membro è sempre positivo in quanto valore assoluto, mentre il secondo membro è sempre positivo in quanto radice quadrata. Osserviamo inoltre che al secondo membro basta soltanto eliminare la radice, mentre al primo membro dobbiamo calcolare il quadrato di un trinomio. Si ha:

\begin{align*} &\cancel{a_s^2x_P^2}+\cancel{b_s^2y_P^2}+c_s^2+2a_sb_sx_Py_P+2a_sc_sx_P+2b_sc_sy_P=\\ \\ & =\scriptsize{a_s^2x_F^2-2a_s^2x_Fx_P+\cancel{a_s^2x_P^2}+a_s^2y_F^2-2a_s^2y_Fy_P+a_s^2y_P^2+b_s^2x_F^2-2b_s^2x_Fx_P+b_s^2x_P^2+b_s^2y_F^2-2b_s^2y_Fy_P+\cancel{b_s^2y_P^2}}\end{align*}

Adesso conviene indicare le coordinate del punto {P} semplicemente con {x} e {y}, poiché effettivamente l’equazione è soddisfatta da un qualunque punto appartenente alla parabola. Proseguiamo inoltre i passaggi raccogliendo opportunamente i termini, come segue:

\begin{align*} &c_s^2+2a_sb_sxy+2a_sc_sx+2b_sc_sy -a_s^2x_F^2+2a_s^2x_Fx-a_s^2y_F^2+\\ \\ & +2a_s^2y_Fy-a_s^2y^2-b_s^2x_F^2+2b_s^2x_Fx-b_s^2x^2-b_s^2y_F^2+2b_s^2y_Fy=0; \\ \\ &  -b_s^2x^2-a_s^2y^2+(2a_sc_s+2a_s^2x_F+2b_s^2x_F)x+\left( 2b_sc_s+2a_s^2y_F+2b_s^2y_F\right)y+ \\ \\ & +2a_sb_sxy+c_s^2-a_s^2x_F^2-a_s^2y_F^2-b_s^2x_F^2-b_s^2y_F^2=0; \\ \\ & -b_s^2x^2-a_s^2y^2+(2a_sc_s+2a_s^2x_F+2b_s^2x_F)x+\left( 2b_sc_s+2a_s^2y_F+2b_s^2y_F\right)y+ \\ \\ & +2a_sb_sxy-x_F^2(a_s^2+b_s^2)-y_F^2(a_s^2+b_s^2)+c_s^2=0  \end{align*}

L’equazione, sicuramente ingombrante, è riesprimibile sinteticamente come:

\boxed{Ax^2+By^2+Cx+Dy+Exy+F=0}

ponendo:

\begin{align*} &A=-b_s^2, \qquad B=-a_s^2, \qquad C=2a_sc_s+2a_s^2x_F+2b_s^2x_F, \\ \\ & D=2b_sc_s+2a_s^2y_F+2b_s^2y_F, \qquad E=2a_sb_s, \\ \\ & F=-x_F^2(a_s^2+b_s^2)-y_F^2(a_s^2+b_s^2)+c_s^2\end{align*}

ovvero se preferite, eseguendo ulteriori raccoglimenti e ponendo {H=a_s^2+b_s^2}:

\begin{align*} &A=-b_s^2, \qquad B=-a_s^2, \qquad C=2(a_sc_s+Hx_F), \\ \\ & D=2(b_sc_s+Hy_F), \qquad E=2a_sb_s, \\ \\ & F=H\cdot(-x_F^2-y_F^2)+c_s^2\end{align*}

L’equazione evidenziata nel riquadro è in conclusione l’equazione in forma implicita di una parabola avente fuoco {F=(x_F, y_F)} e direttrice data da una retta {s:a_sx+b_sy+c_s=0}. Disponiamo quindi in conclusione dell’equazione di una parabola con direttrice qualsiasi, ovvero con asse di simmetria anche obliquo.

Le formule dei coefficienti dell’equazione in forma implicita di una parabola con direttrice qualsiasi sono piuttosto scomode da ricordare, e da questo capiamo perché le parabole con asse di simmetria anche obliquo non sono argomento solitamente trattato nelle scuole superiori.

Esempio 1 (equazione in forma implicita di una parabola con asse di simmetria obliquo)

Determinare l’equazione in forma implicita della parabola avente direttrice {s:3x+4y-6=0} e fuoco {F=(2,2)}.

Scriviamo l’equazione di tale parabola utilizzando la forma:

Ax^2+By^2+Cx+Dy+Exy+F=0

Calcoliamo i valori dei coefficienti (la quantità {H} serve solo per calcolare più rapidamente i coefficienti):

\small \begin{align*} &H=a_s^2+b_s^2=3^2+4^2=9+16=25; \\ \\ &A=-b_s^2=-16, \qquad B=-a_s^2=-9, \qquad C=2(a_sc_s+Hx_F)=2\cdot[3\cdot(-6)+25 \cdot 2]=64, \\ \\ & D=2(b_sc_s+Hy_F)=2 \cdot[4 \cdot (-6)+25 \cdot 2]=52, \qquad E=2a_sb_s=24, \\ \\ & F=H\cdot(-x_F^2-y_F^2)+c_s^2=25 \cdot (-2^2-2^2)+(-6)^2=25 \cdot (-8)+36=-164\end{align*}

L’equazione della parabola in esame è quindi:

-16x^2-9y^2+64x+52y+24xy-164=0

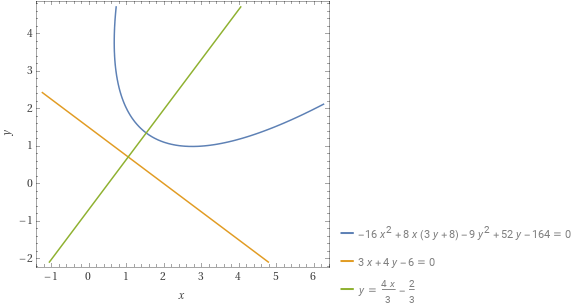
In figura abbiamo anche rappresentato l’asse di simmetria della parabola, che è la retta perpendicolare alla direttrice e tale da passare per il fuoco della parabola.

Per scrivere l’equazione dell’asse di simmetria, osserviamo anzitutto che l’equazione della direttrice è riesprimibile in forma esplicita come:

3x+4y-6=0 \quad \Rightarrow \quad s: y=-\dfrac{3}{4}x+\dfrac{3}{2}

Così, il coefficiente angolare della direttrice della parabola è {m=-\dfrac{3}{4}}. Di conseguenza, il coefficiente angolare dell’asse di simmetria della parabola, che è perpendicolare alla direttrice, è {m'=\dfrac{4}{3}}.

Pertanto, l’asse di simmetria della parabola avrà equazione:

\begin{align*} &y-y_F=\dfrac{4}{3}(x-x_F) \quad \Rightarrow \quad y-2=\dfrac{4}{3}(x-2) \quad \Rightarrow \: y=\dfrac{4}{3}x-\dfrac{2}{3} \end{align*}

e corrisponde alla retta in verde rappresentata in figura.

Parabola con direttrice parallela ad uno degli assi coordinati (a partire dalla parabola con asse obliquo)

Dal caso generale appena studiato è possibile ritrovare i due casi particolari a noi già noti di parabole con direttrici parallele, rispettivamente, agli assi {x} e {y}.

In particolare, se la direttrice {s} della parabola è parallela all’asse delle {x}, la direttrice stessa corrisponderà ad una retta orizzontale ed avrà equazione:

s:y=-c_s

da cui {a_s=0} e {b_s=1}. In tal caso l’equazione della parabola si riduce a:

\begin{align*} &-b_s^2x^2-a_s^2y^2+(2a_sc_s+2a_s^2x_F+2b_s^2x_F)x+\left( 2b_sc_s+2a_s^2y_F+2b_s^2y_F\right)y+ \\ \\ & +2a_sb_sxy-x_F^2(a_s^2+b_s^2)-y_F^2(a_s^2+b_s^2)+c_s^2=0 \quad \text{con} \quad a_s=0, \: b_s=1 \\ \\ & \Rightarrow-x^2+2x_Fx+2c_sy+2y_Fy-x_F^2-y_F^2+c_s^2=0\end{align*}

ovvero esplicitando la {y}:

\begin{align*} &-x^2+2x_Fx+2(c_s+y_F)y-x_F^2-y_F^2+c_s^2=0; \\ \\ & 2(c_s+y_F)y=x^2-2x_Fx+x_F^2+y_F^2-c_s^2; \\ \\ & y=\dfrac{1}{2(c_s+y_F)}x^2-\dfrac{2x_F}{2(c_s+y_F)}x+\dfrac{x_F^2+y_F^2-c_s^2}{2(c_s+y_F)};\\ \\ &y=\dfrac{1}{2(c_s+y_F)}x^2-\dfrac{x_F}{c_s+y_F}x+\dfrac{x_F^2+y_F^2-c_s^2}{2(c_s+y_F)}\end{align*}

A questo punto se esprimiamo per comodità l’equazione della retta direttrice della parabola nella forma:

s: y=d

si ha {c_s=-d} e la precedente diviene:

\begin{align*} &y=\dfrac{1}{2(-d+y_F)}x^2-\dfrac{x_F}{-d+y_F}x+\dfrac{x_F^2+y_F^2-d^2}{2(-d+y_F)}\end{align*}

ovvero riordinando i termini all’interno delle parentesi ai denominatori:

\begin{align*} &y=\dfrac{1}{2(y_F-d)}x^2-\dfrac{x_F}{y_F-d}x+\dfrac{x_F^2+y_F^2-d^2}{2(y_F-d)}\end{align*}

Infine ponendo {a=\dfrac{1}{2(y_F-d)}}, {b=-\dfrac{x_F}{y_F-d}} e {c=\dfrac{x_F^2+y_F^2-d^2}{2(y_F-d)}} otteniamo in definitiva:

\boxed{y=ax^2+bx+c}

e questa è l’equazione di una parabola con direttrice parallela all’asse delle {x}, e quindi con asse di simmetria parallelo all’asse {y}.

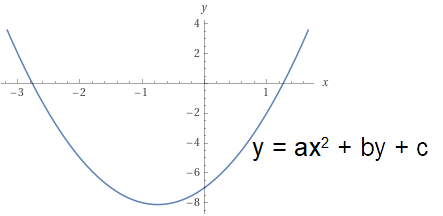
Procedendo allo stesso modo, se la direttrice è della forma:

x=d

abbiamo {a_s=1, b_s = 0} e si ottiene che l’equazione della parabola avente tale direttrice e fuoco {F=(x_F, y_F)} è:

\boxed{x=ay^2+by+c}

ove ai coefficienti {a,b,c} corrispondono le medesime espressioni precedentemente scritte.

Quest’ultima in particolare è l’equazione di una parabola con direttrice parallela all’asse {y}, e quindi con asse di simmetria parallelo all’asse {x}.

Determinazione dell’equazione della direttrice e delle coordinate del fuoco a partire dall’equazione in forma implicita di una parabola

Supponiamo che ci venga data l’equazione in forma implicita di una parabola:

Ax^2+By^2+Cx+Dy+Exy+F=0

In questa lezione ipotizzeremo che una tale equazione sia già verificata come appartenente ad una parabola. Osserviamo infatti che in generale un’equazione di questa forma non sempre appartiene ad una parabola. Ciò dipende in particolare dai valori dei coefficienti dei suoi termini. In altre parole, se attribuiamo a tali termini dei valori reali arbitrari, potremmo incorrere in un’equazione che non rappresenta una parabola. Se invece calcoliamo i termini secondo le espressioni precedentemente fornite, da tale equazione otterremo sempre una parabola.

Il nostro obiettivo è ora determinare, a partire dall’equazione in forma implicita di una parabola, l’equazione della sua direttrice e le coordinate del suo fuoco. In altre parole, si tratterà di ricavare i coefficienti {a_s, b_s, c_s} dell’equazione in forma implicita della direttrice e le coordinate {x_F, y_F} del fuoco.

Cominciamo ricordando le espressioni dei coefficienti {A} e {B}:

A=-b_s^2, \qquad B=-a_s^2

Volendo ricavare i valori dei coefficienti {b_s} ed {a_s}, invertendo tali formule si ha:

b_s^2=-A, \qquad a_s^2=-B

ovvero:

\boxed{b_s=\pm\sqrt{-A}, \qquad a_s=\pm \sqrt{-B}}

Da tali espressioni discendono due osservazioni.

In primo luogo, affinché sia possibile estrarre le radici quadrate, i coefficienti {A} e {B} dovranno essere negativi. Di conseguenza, se nell’equazione data i coefficienti {A} e {B} sono positivi, prima di tutto dovremo cambiare il segno di tutti i termini dell’equazione (ciò in forza del secondo principio di equivalenza).

Inoltre, poiché il segno davanti alla radice è indeterminato (abbiamo un simbolo {\pm}), come facciamo a determinare il segno di ciascun coefficiente? Per questo ci viene in aiuto il segno del coefficiente {E}, dato dal prodotto dei due coefficienti:

E=2a_sb_s

Osserviamo che il segno di {E} dipende dal segno dei coefficienti {a_s} e {b_s}. Infatti, al secondo membro dell’uguaglianza abbiamo il doppio prodotto dei due coefficienti. Di conseguenza, dovremo stabilire i segni di {a_s} e {b_s} necessariamente in modo tale da rispettare il segno di {E}. Così, in pratica, se {E} è negativo dovremo fare in modo che {a_s} e {b_s} siano discordi, mentre se {E} è positivo dovremo fare in modo che {a_s} e {b_s} siano concordi. Ciò discende direttamente dalla regola dei segni relativa ai prodotti.

Ora, nello scegliere i segni dei coefficienti {a_s} e {b_s}, pur rispettando il segno di {E} si hanno comunque due differenti alternative. Ciò non è comunque un problema perché come vedremo ricaveremo il rimanente coefficiente {c_s} coerentemente con i segni scelti per {a_s} e {b_s}.

A questo punto possiamo ricavare la quantità {H}:

H=a_s^2+b_s^2

Ora, per determinare le coordinate del fuoco e il rimanente coefficiente {c_s} dell’equazione della retta direttrice, osserviamo che dalle relazioni:

C=2(a_sc_s+Hx_F),  \qquad D=2(b_sc_s+Hy_F)

si ottiene rispettivamente:

\begin{align*} &C=2a_sc_s+2Hx_F \quad \Rightarrow \quad x_F=\dfrac{C-2a_sc_s}{2H}\end{align*}

e:

D=2b_sc_s+2Hy_F \quad \Rightarrow \quad  y_F=\dfrac{D-2b_sc_s}{2H}

Inoltre deve anche valere la relazione:

 F=H\cdot(-x_F^2-y_F^2)+c_s^2

Abbiamo quindi il sistema di tre equazioni in tre incognite:

\begin{cases}  x_F=\dfrac{C-2a_sc_s}{2H} \\ \\    y_F=\dfrac{D-2b_sc_s}{2H} \\ \\   F=H\cdot(-x_F^2-y_F^2)+c_s^2\end{cases}

Per risolvere il sistema, basta sostituire le espressioni di {x_F} e {y_F} date dalle prime due equazioni nella terza equazione. Considerando separatamente quest’ultima si ha:

\begin{align*} &F=H \cdot \left[ -\left( \dfrac{C-2a_sc_s}{2H}\right)^2-\left( \dfrac{D-2b_sc_s}{2H}\right)^2\right]+c_s^2; \\ \\ & F=H\cdot \left( \dfrac{-C^2+4Ca_sc_s-4a_s^2c_s^2-D^2+4Db_sc_s-4b_s^2c_s^2}{4H^2}\right)+c_s^2;\\ \\ & F=\dfrac{-C^2+4Ca_sc_s-4a_s^2c_s^2-D^2+4Db_sc_s-4b^2_sc_s^2+4Hc_s^2}{4H}  \end{align*}

Proseguiamo i passaggi eseguendo opportunamente dei raccoglimenti, in modo da ritrovare un fattore uguale alla quantità {H}. Poi, procediamo isolando {c_s}.

\begin{align*} &F=\dfrac{-C^2+4Ca_sc_s-\cancel{4(\overbrace{a_s^2+b_s^2}^{H})c_s^2}-D^2+4Db_sc_s+\cancel{4Hc_s^2}}{4H}; \\ \\& F =\dfrac{-C^2-D^2+4c_s(Ca_s+Db_s)}{4H};\\ \\ & \dfrac{-C^2-D^2-4HF+4c_s(Ca_s+Db_s)}{4H}=0;\\ \\ & 4c_s(Ca_s+Db_s)=C^2+D^2+4HF, \qquad H \neq 0; \\ \\ & \boxed{c_s=\dfrac{C^2+D^2+4HF}{4(Ca_s+Db_s)}}\end{align*}

Come evidente l’espressione per {c_s} ottenuta dipende dai valori dei coefficienti {a_s} e {b_s} e quindi fornisce un valore di {c_s} che tiene conto dei segni scelti per {a_s} e {b_s}.

E’ quindi possibile ricavare il valore di {c_s} dall’ultima uguaglianza scritta, e infine i valori delle coordinate {x_F} e {y_F} del fuoco tramite le relazioni già viste in precedenza:

 \boxed{x_F=\dfrac{C-2a_sc_s}{2H}, \qquad y_F=\dfrac{D-2b_sc_s}{2H}}

Vediamo ora di mettere in pratica tutte le formule ottenute con un esempio. In particolare, determiniamo l’equazione della direttrice e le coordinate del fuoco della parabola relativa all’esempio precedente.

Esempio 2

Determinare l’equazione della direttrice e le coordinate del fuoco della parabola di equazione in forma implicita {-16x^2-9y^2+64x+52y+24xy-164=0}.

L’equazione è della forma {Ax^2+By^2+Cx+Dy+Exy+F=0}, con {A=-16, B=-9, C=64, D=52, E=24} ed {F=-164}.

Cominciamo ricavando i coefficienti {a_s} e {b_s}.

In questo caso, osserviamo che non dobbiamo cambiare il segno di tutti i termini dell’equazione. Infatti i coefficienti dei termini di secondo grado sono negativi. Quindi, in base a come abbiamo precedentemente stabilito la formule per i coefficienti {A,B,C,D,E,F} non abbiamo problemi.

Ricordiamo che se invece i coefficienti di secondo grado dell’equazione della parabola sono positivi, occorre cambiare i segni di tutti i termini. Diversamente, non sarebbe possibile estrarre le radici quadrate per ricavare i coefficienti {a_s} e {b_s}.

Per i coefficienti {a_s} e {b_s} abbiamo:

b_s=\pm\sqrt{-A}=\pm \sqrt{-(-16)}=\pm 4, \qquad a_s=\pm \sqrt{-B}=\pm\sqrt{-(-9)}=\pm 3

Ora, per la scelta del segno da attribuire ai coefficienti {a_s} e {b_s} dobbiamo controllare il segno di {E}. Poiché nel nostro caso il segno di {E} è positivo, i due coefficienti devono essere concordi. Possiamo indifferentemente sceglierli entrambi positivi o entrambi negativi, ad esempio:

b_s=4, \qquad a_s=3

Effettivamente ritroviamo correttamente {E=2a_sb_s=2 \cdot 3 \cdot 4 = 24}.

Calcoliamo ora la quantità {H}, necessaria per i calcoli successivi:

H=\sqrt{a_s^2+b_s^2}=\sqrt{3^2+4^2}=25

A questo punto calcoliamo il coefficiente {c_s}:

\begin{align*} &c_s=\dfrac{C^2+D^2+4HF}{4(Ca_s+Db_s)}=\dfrac{64^2+52^2+4 \cdot 25 \cdot (-164)}{4 \cdot (64 \cdot 3 + 52 \cdot 4)}=\dfrac{4096+2704-16400}{4\cdot(192+208)}=\\ \\ & =\dfrac{-9600}{1600}=-6\end{align*}

Disponiamo così di tutti e tre i coefficienti dell’equazione in forma implicita della retta direttrice, per la quale ritroviamo correttamente l’equazione:

s:a_sx+b_sy+c_s=0 \quad \Rightarrow \quad s:3x+4y-6=0

Osserviamo che la scelta alternativa per i segni di {a_s} e {b_s} avrebbe portato all’equazione {-3x-4y+6=0}, comunque equivalente a quella appena ottenuta.

Ci rimangono da determinare le coordinate del fuoco, ovvero i valori {x_F} ed {y_F}. Abbiamo:

\begin{align*} &x_F=\dfrac{C-2a_sc_s}{2H} =\dfrac{64-2 \cdot 3 \cdot (-6)}{2 \cdot 25}=\dfrac{64+36}{50}=\dfrac{100}{50}=2;\\ \\ & y_F=\dfrac{D-2b_sc_s}{2H}=\dfrac{52-2 \cdot 4 \cdot (-6)}{2 \cdot 25}=\dfrac{52+48}{50}=\dfrac{100}{50}=2\end{align*}

Ritroviamo così correttamente il fuoco:

F=(2,2)

Per concludere la lezione sulla parabola con asse di simmetria anche obliquo vediamo un altro esempio.

Esempio 3

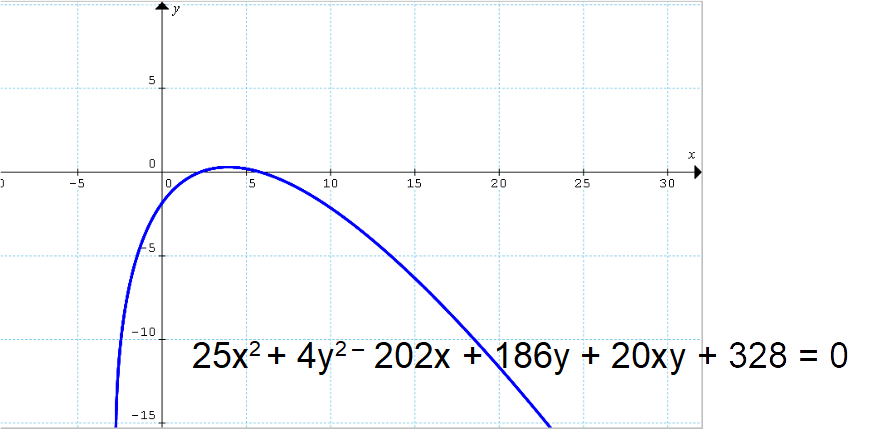
Determinare equazione della retta direttrice e coordinate del fuoco della parabola avente equazione in forma implicita {25x^2+4y^2-202x+186y+20xy+328=0}.

Osserviamo che i coefficienti dei termini di secondo grado sono positivi. Per cui, per come abbiamo dato le formule per il calcolo dei coefficienti {A,B,C,D,E,F} dobbiamo fare in modo che i segni di tali coefficienti siano negativi. Di conseguenza, dobbiamo invertire i segni di tutti i termini dell’equazione:

-25x^2-4y^2+202x-186y-20xy-328=0

A questo punto possiamo assegnare i valori dei coefficienti:

A=-25, B=-4, C=202, D=-186, E=-20, F=-328

Per i coefficienti {a_s} e {b_s} abbiamo:

b_s=\pm\sqrt{-A}=\pm\sqrt{-(-25)}=\pm5, \qquad a_s=\pm\sqrt{-B}=\pm\sqrt{-(-4)}=\pm 2

Ora, il coefficiente {E} ha segno negativo e pertanto i due coefficienti {a_s} e {b_s} devono essere discordi (segno differente). Scegliamo ad esempio i valori:

a_s=2; \qquad b_s=-5

Ricaviamo la quantità {H}:

H=a_s^2+b_s^2=2^2+(-5)^2=4+25=29

A questo punto procediamo calcolando il valore del coefficiente {c_s}:

\begin{align*} &c_s=\dfrac{C^2+D^2+4HF}{4(Ca_s+Db_s)}=\dfrac{202^2+(-186)^2+4 \cdot 29 \cdot (-328)}{4 \cdot (202 \cdot 2+(-186)\cdot(-5)}=\\ \\ & =\dfrac{40804+34596-38048}{4\cdot(404+930)}=\dfrac{37352}{5336}=7\end{align*}

Disponiamo così di tutti e tre i coefficienti dell’equazione in forma implicita della direttrice della parabola, che ha equazione:

s:a_sx+b_sy+c_s \quad \Rightarrow \quad s:2x-5y+7

ovvero se preferite in forma esplicita:

s: y=\dfrac{2}{5}x+\dfrac{7}{5}

Infine calcoliamo le coordinate del fuoco della parabola:

\begin{align*} &x_F=\dfrac{C-2a_sc_s}{2H} =\dfrac{202-2 \cdot 2 \cdot 7}{2 \cdot 29}=\dfrac{202-28}{58}=\dfrac{174}{58}=3;\\ \\ & y_F=\dfrac{D-2b_sc_s}{2H}=\dfrac{-186-2 \cdot (-5)\cdot7}{58}=\dfrac{-186 +70}{58}=\dfrac{-116}{58}=-2\end{align*}

Così in conclusione il fuoco della parabola in esame è:

F=(3,-2)

Infine, come riprova, vediamo se a partire dall’equazione della direttrice e dalle coordinate del fuoco appena determinate ritroviamo l’equazione in forma implicita della parabola di partenza. Abbiamo:

\small \begin{align*} &H=a_s^2+b_s^2=2^2+(-5)^2=29; \\ \\ &A=-b_s^2=-(-5)^2=-25 \qquad B=-a_s^2=-(-2)^2=-4, \\ \\ &C=2(a_sc_s+Hx_F)=2 \cdot (2 \cdot 7+29 \cdot 3)=2\cdot(14+87)=202, \\ \\ & D=2(b_sc_s+Hy_F)=2\cdot[-5\cdot7+29\cdot(-2)]=2 \cdot (-93)=-186, \\ \\ & E=2a_sb_s=2 \cdot 2 \cdot (-5)=-20, \\ \\ & F=H\cdot(-x_F^2-y_F^2)+c_s^2=29 \cdot [-3^2-(-2)^2]+7^2=29\cdot(-9-4)+49=-328\end{align*}

Ritroviamo così per la parabola l’equazione:

-25x^2-4y^2+202x-186y-20xy-328=0

ovvero, invertendo i segni di tutti i termini:

25x^2+4y^2-202x+186y+20xy+328=0

Conclusioni

Per quanto riguarda lo studio della parabola con asse di simmetria anche obliquo (direttrice qualsiasi) ci fermiamo qui. Ribadiamo ancora una volta che le parabole di questo genere non vengono trattate alle scuole superiori. In tale contesto, infatti, sono di interesse soltanto le parabole con asse di simmetria parallelo ad uno degli assi coordinati. Tuttavia, abbiamo ritenuto utile presentare il caso più generale, mostrando come sia possibile affrontarlo anche utilizzando nozioni di geometria analitica non particolarmente avanzate. Qui in particolare ce la siamo cavata utilizzando la formula della distanza punto-retta e la formula della distanza tra due punti del piano.

Un saluto a tutti voi e, come sempre, buono studio con SìMatematica!