Parabola

 - 

Parabola (scuole superiori)

La parabola è il luogo geometrico dei punti aventi la stessa distanza da una particolare retta detta direttrice e da un fissato punto detto fuoco, tale da non appartenere alla direttrice.

L’equazione della parabola è y = ax² + bx + c se l’asse di simmetria della parabola è verticale (direttrice orizzontale) oppure x = ay² + by + c se l’asse di simmetria della parabola è orizzontale (direttrice verticale). L’asse di simmetria della parabola è in ogni caso tale da essere perpendicolare alla direttrice ed è tale da passare per un particolare punto della parabola detto vertice. I coefficienti a, b, c sono numeri reali, con a ≠ 0.

Osserviamo che in generale la direttrice di una parabola può essere una retta qualunque. In tal caso l’equazione della parabola si scrive in forma implicita come Ax² + By² + Cx + Dy + Exy + F = 0, con opportune ipotesi sui valori dei coefficienti (vedi: parabola con asse obliquo). Tuttavia, nell’ambito delle scuole superiori si considerano tipicamente i soli due casi di parabole con direttrice parallela ad uno degli assi coordinati.

In questa lezione considereremo entrambi i casi di parabole con assi paralleli all’asse {x} e all’asse {y}, mostrando come ricavare le corrispondenti equazioni a partire dalla definizione di parabola come luogo geometrico. Infine, presenteremo degli esempi su come determinare l’equazione di una parabola a partire dalla direttrice e dal fuoco e viceversa su come determinare le coordinate del fuoco, del vertice e l’equazione della direttrice di una parabola a partire dall’equazione della parabola stessa.

Precisiamo che nella presente lezione forniremo moltissime dimostrazioni, con l’obiettivo di consentire l’acquisizione di una buona padronanza degli argomenti. Nelle successive lezioni ci concentreremo invece di più sulle formule e i relativi esempi, rivedendo le dimostrazioni soltanto nella parte finale di ciascuna lezione.

Definizione di parabola come luogo geometrico

Consideriamo una retta {s} parallela ad esempio all’asse {x}, detta direttrice, e un punto a nostra scelta {F=(x_F, y_F)}, detto fuoco, tale da non appartenere alla retta {s}. In particolare, nel caso in esame la retta {s} è orizzontale ed ha equazione:

s: y = d, \qquad d \in \R

Importante. Secondo le convenzioni qui adottate, indichiamo con {s} la direttrice e con {d} il valore presente al secondo membro dell’equazione della direttrice.

Poiché il fuoco per ipotesi non appartiene alla direttrice {s}, questo avrà ordinata diversa da {d}. Varrà pertanto la condizione:

y_F \neq d

Rappresentiamo la retta {s} ed il punto {F} nel piano cartesiano:

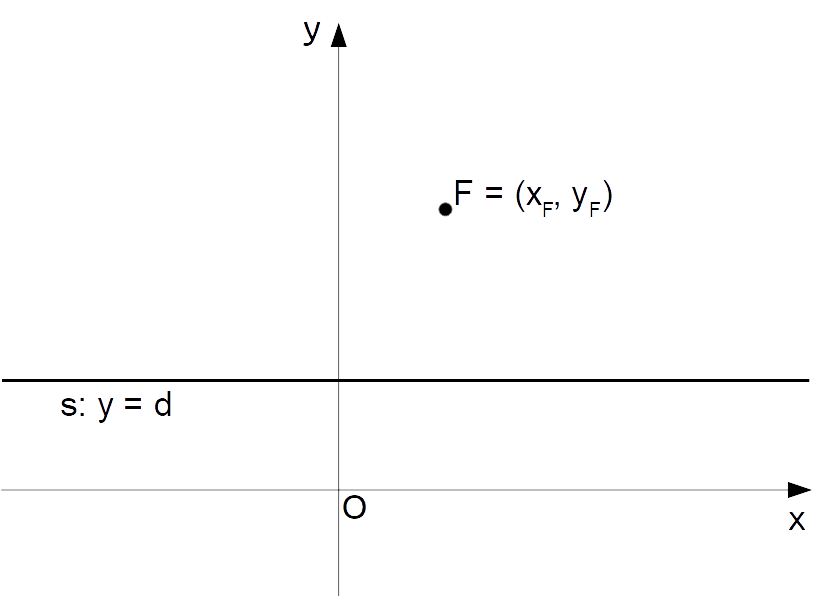
Per definizione, la parabola è l’insieme dei punti {P=(x,y)} del piano cartesiano tali da avere la stessa distanza dalla direttrice {s} e dal fuoco {F}. Così, ogni punto della parabola dovrà verificare l’uguaglianza:

d(P,s)=d(P,F)

ove al primo membro abbiamo la distanza tra il punto {P} e la direttrice {s} (vedi: distanza punto-retta), mentre al secondo membro abbiamo la distanza tra i due punti {P} ed {F}.

Un punto della parabola è ad esempio il punto {P} riportato a seguire:

Il punto {P=(x,y)} ha infatti coordinate tali che la distanza tra il punto {P} e il fuoco {F} è uguale alla distanza tra il punto {P} e la retta {s}.

Consideriamo ora altri punti della parabola. Per individuarli, esiste una determinata costruzione grafica. In particolare, dobbiamo rappresentare delle rette parallele ad {s}, e considerare la distanza tra ciascuna retta tracciata e la retta {s}. Tale distanza sarà, per ogni retta, l’apertura del compasso. In questo modo, per ciascuna retta dovremo collocare la punta del compasso nel fuoco {F}, in modo da individuare sulla retta parallela corrente, rotando il compasso, due punti. Tali punti appartengono alla parabola.

Così, tracciando un certo numero di rette parallele alla direttrice della parabola sarà possibile individuare un insieme di punti appartenenti alla parabola, unendo i quali si otterrà la curva corrispondente alla parabola stessa.

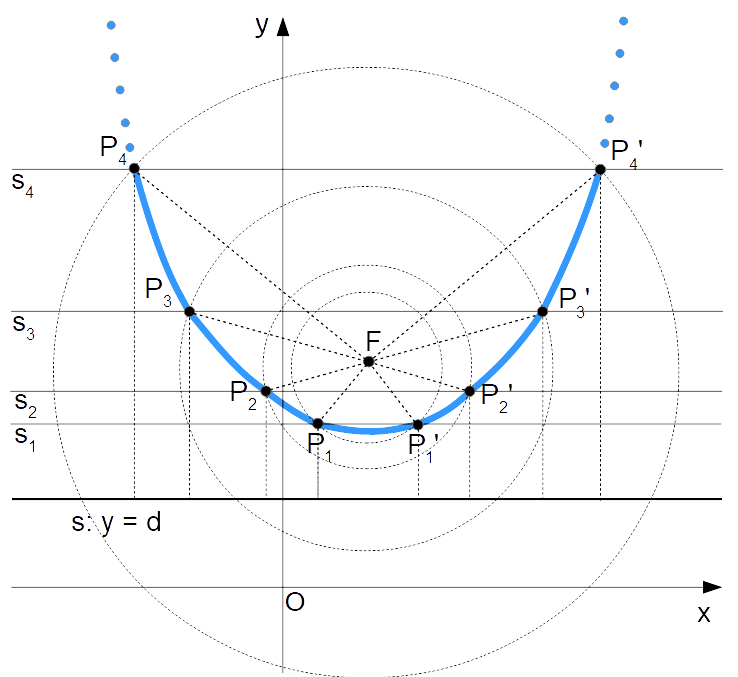
Importante: nella figura abbiamo per forza di cose considerato un numero finito di punti, ma in realtà una parabola è costituita da infiniti punti. Inoltre i suoi “rami” (ovvero le sue “estremità”) si estendono all’infinito.

L’asse di simmetria della parabola è la retta perpendicolare alla direttrice e passante per il fuoco, ovvero in questo caso (direttrice orizzontale) la retta verticale di equazione:

x=x_F

L’asse di simmetria incontra la parabola in un particolare punto {V} detto vertice. Quest’ultimo è dunque ottenibile dall’intersezione della parabola con l’asse verticale {x=x_F}, e presenta la particolarità di essere il punto della parabola caratterizzato dalla minima distanza rispetto alla direttrice.

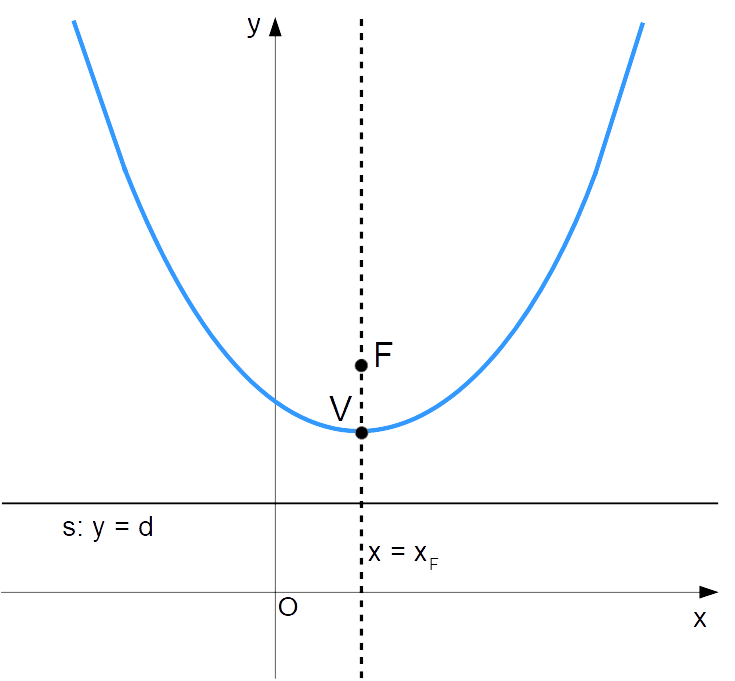
Equazione di una parabola con asse di simmetria parallelo all’asse y

Osserviamo che per la distanza tra un generico punto {P=(x,y)} appartenente alla parabola e il fuoco {F} si ha:

d(P,F)=\overline{PF}=\sqrt{(x_F-x)^2+(y_F-y)^2}

Ciò discende dalla formula della distanza tra due punti nel piano.

Per la distanza tra la retta direttrice {s} e il punto {P} si ha invece:

d(P,s)=|y-d|

Ciò discende dalla formula della distanza punto-retta, ma basta semplicemente ricordare che la distanza tra un punto e una retta è misurata lungo la perpendicolare alla retta data passante per il punto stesso. Così, nel nostro caso la distanza tra il punto {P} e la direttrice {s} si ottiene come il valore assoluto della differenza tra l’ordinata del punto {P} e l’ordinata comune a tutti i punti della direttrice {s}, ovvero {d}.

Volendo comunque utilizzare la formula della distanza punto-retta, abbiamo:

d(P,s)=\dfrac{|a_sx+b_sy+c_s|}{\sqrt{a^2+b^2}}=\dfrac{|0 \cdot x + 1 \cdot y -d|}{\sqrt{0^2+1^2}}=|y-d|

Per comprendere i passaggi, osserviamo che confrontando l’equazione {s:y-d=0} con l’equazione in forma implicita di una generica retta {s}, ovvero {s:a_sx+b_sy+c_s=0}, nel nostro caso abbiamo {a_s=0, b_s=1, c_s = -d}.

Se preferite, sempre in base alla definizione della distanza tra un punto e una retta, possiamo in alternativa considerare il punto {H} dato dall’intersezione tra la direttrice {s} della parabola e la retta verticale passante per il punto {P}:

Come è evidente, la distanza tra il punto {P} e la retta direttrice {s} coincide con la distanza tra i due punti {P} e {H}:

\overline{PH}=\sqrt{(x_H-x)^2+(\underbrace{y_H}_{d}-y)^2}=\sqrt{(d-y)^2}=|d-y|=|y-d|

Può essere utile precisare che essendo i punti {P} ed {H} allineati verticalmente si ha {x_H = x}, e quindi {x_H-x=0}. Inoltre, ci ritroviamo nel risultato con un valore assoluto per una delle proprietà fondamentali dei radicali.

Tenendo conto di tutto quanto sin qui detto, l’uguaglianza precedentemente scritta, ovvero:

d(P,s)=d(P,F)

diviene:

|y-d|=\sqrt{(x_F-x)^2+(y_F-y)^2} \qquad (*)

Così, ciascun punto della parabola dovrà verificare l’uguaglianza appena scritta. E questa è già una prima forma dell’equazione della parabola, che discende direttamente dalla sua definizione come luogo geometrico di punti. Tuttavia, ci ritroviamo al momento con un’equazione irrazionale.

Ora, il nostro obiettivo è ricondurre l’equazione della parabola ad una forma più semplice, ove risulti esplicitata la variabile {y}. Per fare ciò, osserviamo anzitutto che è possibile elevare al quadrato entrambi i membri della *. E ciò non richiede alcuna discussione, in quanto entrambi i membri sono quantità positive. Infatti, al secondo membro abbiamo una radice quadrata, mentre al primo membro abbiamo un valore assoluto. Inoltre, il radicando al secondo membro è una somma di quadrati, quindi una quantità sempre positiva. Di conseguenza, il radicale al secondo membro non richiede alcuna condizione di realtà.

Perciò, elevando direttamente al quadrato entrambi i membri abbiamo:

\begin{align*} &\left(|y-d|\right)^2=\left(\sqrt{(x_F-x)^2+(y_F-y)^2}\right)^2\end{align*}

ovvero:

\begin{align*} &\left(y-d\right)^2={(x_F-x)^2+(y_F-y)^2}\end{align*}

Sviluppiamo i quadrati, e quindi riordiniamo i termini cercando di isolare la {y}:

\begin{align*} &\cancel{y^2}-2dy+d^2=x_F^2-2x_Fx+x^2+y_F^2-2y_Fy+\cancel{y^2} \\ \\ &-2dy+2y_Fy=x_F^2-2x_Fx+x^2+y_F^2-d^2;\\ \\ & 2y(y_F-d)=x^2-2x_Fx+x_F^2+y_F^2-d^2; \\ \\ & y=\dfrac{1}{2(y_F-d)}x^2+\dfrac{-\cancel{2}x_F}{\cancel{2}(y_F-d)}x+\dfrac{x_F^2+y_F^2-d^2}{2(y_F-d)}, \qquad y_F -d \neq 0\end{align*}

Osserviamo che la condizione {y_F - d \neq 0}, ovvero {y_F \neq d} è soddisfatta poiché per definizione il fuoco non appartiene alla direttrice {s: y=d}, e quindi non può avere ordinata {d}.

Otteniamo così l’equazione:

 y=\dfrac{1}{2(y_F-d)}x^2+\dfrac{-x_F}{y_F-d}x+\dfrac{x_F^2+y_F^2-d^2}{2(y_F-d)}

Tale equazione può essere riscritta in forma compatta ponendo:

a=\dfrac{1}{2(y_F-d)}, \qquad b=\dfrac{-x_F}{y_F-d}, \qquad c=\dfrac{x_F^2+y_F^2-d^2}{2(y_F-d)} \qquad (**)

ottenendo in conclusione:

\boxed{y=ax^2+bx+c, \qquad a \neq 0, \quad a,b,c \in \R} \qquad (1)

Questa è l’equazione di una parabola con direttrice parallela all’asse x, ovvero con asse di simmetria parallelo all’asse y (verticale).

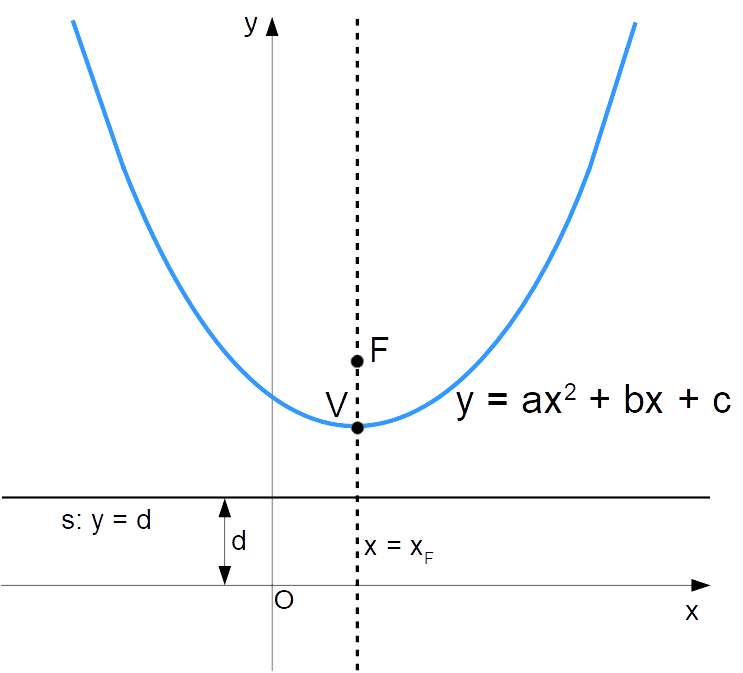
Osserviamo che poiché i coefficienti {a,b,c} dipendono dalle coordinate del fuoco e dalla ordinata {d} comune ai punti della direttrice, l’equazione {(1)} consente di scrivere l’equazione di una parabola con asse verticale a partire dalle coordinate del fuoco {F} e dalla ordinata {d} dei punti della direttrice. Se preferite, la quantità {d} può essere anche vista come la distanza con segno della direttrice {s} rispetto all’asse {x}.

Osservazione. Per “distanza con segno” {d} tra la retta direttrice e l’asse {x} intendiamo la corrispondente distanza alla quale però viene attribuito segno più nel caso in cui la direttrice si trovi al di sopra dell’asse {x} e segno meno nel caso in cui la direttrice si trovi al di sotto dell’asse {x}. Ciò è coerente con il fatto che la quantità {d} rappresenta un’ordinata, quindi una quantità con segno, ed in particolare l’ordinata comune a tutti i punti della retta direttrice.
La precisazione è importante poiché in generale una distanza è soltanto positiva o al più nulla. In questo caso stiamo quindi adottando una definizione particolare.

Il vertice {V} è dato dall’intersezione della parabola con il proprio asse di simmetria. Considerando quindi l’equazione della parabola e l’equazione dell’asse di simmetria, le coordinate del vertice si ottengono mettendo a sistema le due equazioni:

\begin{cases} y=ax^2+bx+c \\ \\ x=x_F\end{cases}

Ciò equivale infatti a ricercare i punti di intersezione tra la parabola e l’asse di simmetria, in modo del tutto simile a quanto visto ad esempio relativamente alla ricerca dei punti di intersezione tra una circonferenza e una retta.

Per risolvere il sistema, del tipo non lineare, è sufficiente procedere per sostituzione. In particolare, si tratta di sostituire l’espressione per {x} fornita dalla seconda equazione al posto di ogni lettera {x} nella prima equazione:

\begin{cases} y=ax_F^2+bx_F+c \\ \\ x=x_F\end{cases}

Se quindi indichiamo rispettivamente con {x_V} ed {y_V} l’ascissa e l’ordinata del vertice, possiamo ricavare le coordinate del vertice a partire dalle coordinate del fuoco come:

V=\left( x_V, y_V\right)=(x_F, ax_F^2+bx_F+c)

Quindi l’ascissa del vertice è uguale all’ascissa del fuoco, mentre l’ordinata del vertice si ottiene sostituendo nell’espressione del secondo membro dell’equazione della parabola l’ascissa del fuoco.

Vediamo subito un esempio su come scrivere le equazioni di parabole con asse di simmetria verticale a partire dalle coordinate del fuoco {F} e dalla distanza con segno {d} della direttrice dall’asse {x}.

Esempio 1

Scrivere l’equazione di una parabola con asse di simmetria verticale, con fuoco {F=(-3,5)} e retta direttrice i cui punti hanno ordinata {d=3}. Calcolare inoltre le coordinate del vertice della parabola stessa.

Dal fatto che la parabola ha asse di simmetria verticale deduciamo immediatamente che la sua direttrice è orizzontale. Quindi, l’equazione della direttrice {s} ha sicuramente forma del tipo:

s: y=d

Inoltre poiché {d=3} abbiamo in particolare:

s:y=3

Essendo poi {F=(-3,5)} abbiamo per le coordinate del fuoco:

x_F=-3, \qquad y_F=5

Disponendo della quantità {d} e delle coordinate del fuoco, possiamo calcolare i coefficienti {a,b,c} relativi all’equazione della parabola grazie alle **.

Nel nostro caso:

\begin{align*} &a=\dfrac{1}{2(y_F-d)} = \dfrac{1}{2(5-3)}=\dfrac{1}{4};\\ \\ & b=\dfrac{-x_F}{y_F-d}=\dfrac{-(-3)}{5-3}=\dfrac{3}{2}; \\ \\ & c=\dfrac{x_F^2+y_F^2-d^2}{2(y_F-d)}=\dfrac{(-3)^2+5^2-3^2}{2(5-3)}=\dfrac{\cancel{9}+25-\cancel{9}}{4}=\dfrac{25}{4}\end{align*}

Essendo ormai noti i valori dei coefficienti {a,b,c} possiamo scrivere l’equazione cercata come:

\begin{align*} &y=ax^2+bx+c \qquad \text{con} \quad a=\dfrac{1}{4}, \: b=\dfrac{3}{2}, \: c= \dfrac{25}{4} \\ \\ & \Rightarrow \quad y=\dfrac{1}{4}x^2+\dfrac{3}{2}x+\dfrac{25}{4}\end{align*}

Questa è dunque l’equazione della parabola con asse di simmetria verticale avente fuoco {F=(-3,5)} e distanza con segno fra la direttrice e l’asse {x} pari a {d=3}.

Per le coordinate del vertice abbiamo infine:

\begin{align*} & V=(x_V, y_V)=\left (x_F, ax_F^2+bx_F+c\right)  \\ \\& \Rightarrow   \quad x_V=-3;\\ \\ &  \Rightarrow  \quad y_V=ax_F^2+bx_F+c=\dfrac{1}{4}\cdot(-3)^2+\dfrac{3}{2} \cdot (-3)+\dfrac{25}{4}=\\ \\ & =\dfrac{1}{4} \cdot 9 - \dfrac{9}{2}+\dfrac{25}{4}=\dfrac{9-18+25}{4}=4\end{align*}

Di conseguenza il vertice {V} della parabola è:

V=(-3,4)

In alternativa, osserviamo che per calcolare le coordinate del vertice {V} è anche possibile impostare il sistema relativo all’intersezione fra la parabola e l’asse di simmetria, specifico per il caso in esame:

\begin{cases} y=\dfrac{1}{4}x^2+\dfrac{3}{2}x+\dfrac{25}{4} \\ \\x =-3 \end{cases}

Per scrivere tale sistema basta ricordare che l’asse di simmetria verticale di una parabola ha equazione della forma {x=x_F}. Sostituendo il valore {-3} nella prima equazione si ritrova il valore già calcolato dell’ordinata del vertice.

Più semplicemente, tuttavia, basta tener conto che per calcolare l’ordinata del vertice basta sostituire il valore dell’ascissa del vertice (e quindi del fuoco) nell’equazione della parabola, ricavando il valore della {y} corrispondente.

Come determinare le coordinate del fuoco, del vertice e l’equazione della direttrice di una parabola con asse verticale

Supponiamo che sia data l’equazione di una parabola con asse di simmetria verticale:

y=ax^2+bx+c=0, \qquad a \neq 0, \quad a,b,c \in \R

I valori dei coefficienti {a, b, c} sono dunque in questo caso noti.

Il nostro obiettivo è determinare, a partire dai coefficienti {a,b,c} le coordinate del fuoco, del vertice e la distanza con segno {d} tra la retta direttrice e l’asse delle {x}.

Per fare ciò, riprendiamo le relazioni grazie alle quali abbiamo calcolato i coefficienti dell’equazione della parabola nell’esempio precedente:

a=\dfrac{1}{2(y_F-d)}, \qquad b=\dfrac{-x_F}{y_F-d}, \qquad c=\dfrac{x_F^2+y_F^2-d^2}{2(y_F-d)} \qquad (**)

Ora i valori dei coefficienti {a,b,c} sono noti, e dobbiamo cercare di ricavare da queste uguaglianze le coordinate {x_F} ed {y_F} del fuoco e la quantità {d}. Inoltre, vedremo poi come determinare anche le coordinate del vertice a partire dai coefficienti {a,b,c}.

Osserviamo che una volta nota la quantità {d}, sarà anche nota l’equazione della direttrice. Per cui determinare l’equazione della direttrice di parabole con asse verticale equivale a determinare la distanza con segno che ha tale direttrice rispetto all’asse delle {x}.

In tutto nelle uguaglianze ** compaiono tre incognite: {x_F, y_F} e {d}. E poiché tali uguaglianze valgono contemporaneamente, per ricavare i valori delle tre incognite l’idea è quella di mettere le ** a sistema:

\begin{cases} a=\dfrac{1}{2(y_F-d)}\\ \\  b=\dfrac{-x_F}{y_F-d} \\ \\ c=\dfrac{x_F^2+y_F^2-d^2}{2(y_F-d)}  \end{cases}

Cominciamo ricavando {x_F} dalla seconda equazione:

\begin{cases} a=\dfrac{1}{2(y_F-d)}\\ \\  b=\dfrac{-x_F}{y_F-d}  \quad \rightarrow \quad x_F=-b\cdot(y_F-d)\\ \\ c=\dfrac{x_F^2+y_F^2-d^2}{2(y_F-d)}  \end{cases}

Omettiamo in questo e nei passaggi a seguire la condizione {y_F - d \neq 0} poiché comunque il fuoco non appartiene alla direttrice, e quindi tale condizione è sicuramente soddisfatta.

A questo punto ricaviamo un’espressione per la quantità {y_F} dalla prima equazione:

\begin{cases} a=\dfrac{1}{2(y_F-d)}  \quad \rightarrow \quad y_F-d = \dfrac{1}{2a}  \quad \rightarrow \: y_F=\dfrac{1}{2a}+d\\ \\   x_F=-b\cdot(y_F-d)\\ \\ c=\dfrac{x_F^2+y_F^2-d^2}{2(y_F-d)}  \end{cases}

Ora sostituiamo l’espressione ottenuta per {y_F} dalla prima equazione nella seconda equazione:

\begin{cases}  y_F=\dfrac{1}{2a}+d\\ \\  x_F=-b\cdot\left( \dfrac{1}{2a}+\cancel{d}-\cancel{d}\right) \quad \rightarrow \quad \boxed{x_F=-\dfrac{b}{2a}}\\ \\ c=\dfrac{x_F^2+y_F^2-d^2}{2(y_F-d)}  \end{cases}

Adesso, sostituiamo le espressioni ottenute per {x_F} ed {y_F} nella terza equazione, in modo da ottenere un’espressione per la quantità {d} che è funzione dei soli coefficienti {a,b,c}. Eseguiamo i calcoli separatamente.

\begin{align*} &c=\dfrac{\left( -\dfrac{b}{2a}\right)^2+\left( \dfrac{1}{2a}+d\right)^2-d^2}{2\cdot\left( \dfrac{1}{2a}+\cancel{d}-\cancel{d}\right)}; \\ \\ & c=\dfrac{\dfrac{b^2}{4a^2}+\left(\dfrac{1+2ad}{2a}\right)^2-d^2}{\cancel{2} \cdot \dfrac{1}{\cancel{2}a}};\\ \\& c=\dfrac{\dfrac{b^2}{4a^2}+\dfrac{1+4a^2d^2+4ad}{4a^2}-d^2}{{\dfrac{1}{a}}};\\ \\ & c=\dfrac{b^2+1+\cancel{4a^2d^2}+4ad-\cancel{4a^2d^2}} {4a^{\cancel{2}}} \cdot \cancel{a}, \qquad a \neq 0;\\ \\ &c=\dfrac{b^2+1+4ad}{4a}\end{align*}

Proseguiamo i passaggi cercando di isolare {d}:

\begin{align*} & \dfrac{b^2+1+4ad-4ac}{\cancel{4a}}=0, \qquad a \neq 0; \\ \\ &4ad=-b^2-1+4ac; \\ \\ & d=\dfrac{-b^2-1+4ac}{4a} \end{align*}

Ora riordiniamo i termini e ricordiamo che dalla teoria sulle equazioni di secondo grado si ha {\Delta = b^2-4ac}:

\begin{align*} &d=\dfrac{-1-b^2+4ac}{4a};\\ \\ & d=\dfrac{-1-(b^2-4ac)}{4a}; \\ \\ &d=\dfrac{-1-\Delta}{4a};\\ \\ & \boxed{d=-\dfrac{1+\Delta}{4a}}\end{align*}

Abbiamo così ottenuto un’espressione per {d} in funzione dei soli coefficienti dell’equazione della parabola. Anche la precedente espressione per {x_F} è in funzione soltanto di tali coefficienti. Ci rimane soltanto da aggiustare l’espressione per {y_F}:

  y_F=\dfrac{1}{2a}+d

Basta sostituire l’espressione appena ottenuta per {d}, ottenendo:

\begin{align*} &y_F=\dfrac{1}{2a}-\dfrac{1+\Delta}{4a}; \\ \\ & y_F=\dfrac{2-1-\Delta}{4a}; \\ \\ & \boxed{y_F=\dfrac{1-\Delta}{4a}}\end{align*}

A questo punto riassumiamo a seguire come ricavare le coordinate del fuoco e l’equazione della direttrice di una parabola con asse verticale.

Data l’equazione di una parabola con asse di simmetria verticale {y=ax^2+bx+c}, le coordinate del fuoco {F=(x_F, y_F)} e la distanza con segno {d} della direttrice {s} rispetto all’asse {x} sono date da:{F=\left(-\dfrac{b}{2a}, \dfrac{1-\Delta}{4a}\right); \qquad d=-\dfrac{1+\Delta}{4a}}ove {\Delta = b^2-4ac}.

Di conseguenza, la direttrice {s} ha equazione:{s:y=-\dfrac{1+\Delta}{4a}}mentre l’asse di simmetria ha equazione:{x=-\dfrac{b}{2a}}

Per quanto riguarda il vertice, osserviamo che questo ha la stessa ascissa del fuoco. Per la sua ordinata, basta sostituire la sua ascissa, e quindi l’ascissa del fuoco, nell’equazione della parabola. Infatti, il vertice è un punto appartenente alla parabola e quindi ne deve soddisfare l’equazione. Poiché {x_F=-\dfrac{b}{2a}}, abbiamo:

\begin{align*} &y=ax^2+bx+c \quad \text{con} \quad x=-\dfrac{b}{2a} \\ \\ & \Rightarrow \quad y=a\cdot\left( -\dfrac{b}{2a}\right)^2+b \cdot \left( -\dfrac{b}{2a}\right)+c; \\ \\ & \Rightarrow \quad y=\cancel{a} \cdot \dfrac{b^2}{4a^{\cancel{2}}}-\dfrac{b^2}{2a}+c; \\ \\ & \Rightarrow \quad y=\dfrac{b^2}{4a}-\dfrac{b^2}{2a}+c;\\ \\ & \Rightarrow \quad y=\dfrac{b^2-2b^2+4ac}{4a};\\ \\ & \Rightarrow \quad {y=\dfrac{-b^2+4ac}{4a}}; \\ \\ & \Rightarrow \quad \boxed{y_V=-\dfrac{\Delta}{4a}}\end{align*}

Quindi, per le coordinate del vertice di parabole con asse di simmetria verticale possiamo concludere quanto segue.

Il vertice {V=(x_V, y_V)} di una parabola con asse di simmetria verticale, ovvero di una parabola con equazione {y=ax^2+bx+c} è:{V=\left( -\dfrac{b}{2a}, -\dfrac{\Delta}{4a}\right)}con {\Delta = b^2-4ac}.

Osserviamo che comunque, invece di ricordare tale formula, come già visto possiamo in alternativa calcolare l’ordinata del vertice sostituendo nell’equazione della parabola direttamente il valore dell’ascissa {x_F} del fuoco. Inoltre, l’ascissa del vertice non deve essere calcolata in quanto è uguale all’ascissa del fuoco. Tuttavia, le formule per le coordinate del vertice sono utili qualora si desideri calcolare tali coordinate direttamente a partire dall’equazione della parabola, senza prima dover calcolare l’ascissa del fuoco.

Abbiamo visto come le formule relative alle coordinate del fuoco, alla distanza con segno {d} della direttrice rispetto all’asse {x} e del vertice sono espresse in funzione del determinante {\Delta}, ovvero la quantità {b^2-4ac}.

Ripensando alle equazioni di secondo grado, data ad esempio l’equazione:

ax^2+bx+c=0

questa ammette due soluzioni reali e coincidenti se:

\Delta=0

In tal caso, sappiamo che la parabola corrispondente all’equazione, ovvero la parabola di equazione:

y=ax^2+bx+c

tocca l’asse delle {x} in un solo punto.

Di tale fatto troviamo conferma nelle formule delle coordinate del vertice. Infatti, per {\Delta=0} si ha:

V=\left( -\dfrac{b}{2a}, -\dfrac{\Delta}{4a}\right)=\left( -\dfrac{b}{2a}, 0\right)

Così l’ordinata del vertice è nulla, il che significa che il vertice appartiene all’asse delle {x}, ovvero alla retta di equazione {y=0}. Ma poiché il vertice è il punto della parabola più vicino alla direttrice, deduciamo immediatamente che questo è l’unico punto della parabola che interseca l’asse delle {x}.

Vediamo ora un esempio su come determinare le coordinate del fuoco, del centro e l’equazione della direttrice a partire dall’equazione di una parabola con asse di simmetria verticale.

Esempio 2

Determinare coordinate del fuoco, del vertice ed equazione della direttrice relativamente alla parabola di equazione {y=5x^2+3x-7}.

Per la forma che ha l’equazione, la parabola ha asse di simmetria verticale, ovvero parallelo all’asse {y}. Di conseguenza, la direttrice della parabola sarà parallela all’asse delle {x}. Infatti, la direttrice di una parabola è sempre perpendicolare all’asse di simmetria.

Poiché l’equazione della parabola in esame è:

y=5x^2+3x-7

confrontandola con l’equazione di una generica parabola con asse di simmetria verticale:

y=ax^2+bx+c

deduciamo per i coefficienti i valori:

a=5, \quad b=3, \quad c=-7

Se non è ben chiaro perché il coefficiente {c} ha segno negativo, osserviamo che possiamo riscrivere l’equazione della parabola come:

y=5x^2+3x+(-7)

da cui ritroviamo {c=-7}.

Per applicare in modo più efficiente le formule, cominciamo calcolando separatamente il valore del determinante {\Delta}:

\Delta = b^2-4ac=3^2-4 \cdot 5 \cdot (-7)=9+140=149

Calcoliamo le coordinate del fuoco. Si ha, sostituendo nella formula corrispondente i valori dei coefficienti dell’equazione e il valore di {\Delta} appena calcolato:

\small \begin{align*} &F=(x_F, y_F)=\left(-\dfrac{b}{2a}, \dfrac{1-\Delta}{4a}\right)=\left( -\dfrac{3}{2 \cdot 5}, \dfrac{1-149}{4 \cdot 5}\right)=\left( -\dfrac{3}{10}, -\dfrac{148}{20}\right)=\left( -\dfrac{3}{10},-\dfrac{37}{5}\right)\end{align*}

Calcoliamo ora la distanza con segno {d} della direttrice rispetto all’asse {x}:

\begin{align*} &d=-\dfrac{1+\Delta}{4a}=-\dfrac{1+149}{4 \cdot 5}=-\dfrac{150}{20}=-\dfrac{15}{2}\end{align*}

Poiché la parabola ha asse di simmetria verticale, la direttrice sarà orizzontale, e quindi della forma {y=d}. Così nel nostro caso l’equazione della direttrice è:

s: y=-\dfrac{15}{2}

Concludiamo calcolando le coordinate del vertice:

\begin{align*} & V=(x_V,y_V)=\left( -\dfrac{b}{2a}, -\dfrac{\Delta}{4a}\right) =\left( -\dfrac{3}{2 \cdot 5}, -\dfrac{149}{4 \cdot 5}\right)=\left( -\dfrac{3}{10}, -\dfrac{149}{20}\right)\end{align*}

Se non ricordiamo le formule delle coordinate del vertice, basta osservare in alternativa che l’ascissa del vertice coincide con l’ascissa del fuoco. Inoltre, l’ordinata del vertice si può ottenere sostituendo l’ascissa del fuoco nell’equazione della parabola:

\begin{align*} &y_V=5x_F^2+3x_F-7 \quad \text{con}\quad x_F=-\dfrac{3}{10} \\ \\ &y_V=5 \cdot \left( -\dfrac{3}{10}\right)^2+3 \cdot \left( -\dfrac{3}{10}\right)-7=5 \cdot \dfrac{9}{100}-\dfrac{9}{10}-7=\\ \\ & =\dfrac{45}{100}-\dfrac{9}{10}-7=\dfrac{45-90-700}{100}=-\dfrac{745}{100}=-\dfrac{149}{20}\end{align*}

Ritroviamo correttamente anche in questo modo, sebbene con più calcoli, le coordinate del vertice.

Concavità di una parabola con asse di simmetria verticale

Con un’approssimazione piuttosto rozza ma presumibilmente efficace, possiamo immaginare la parabola come il profilo di un bicchiere. In tal caso, per concavità di una parabola intendiamo la parte interna del bicchiere.

La concavità di una parabola cambia in base alla posizione del fuoco rispetto alla retta direttrice. In particolare, per una parabola con asse di simmetria verticale:

• se il fuoco si trova al di sopra della retta direttrice, la concavità della parabola è rivolta verso l’alto;
• se invece il fuoco si trova al di sotto della retta direttrice, la concavità della parabola è rivolta verso il basso.

Così, se la concavità è rivolta verso l’alto, l’acqua rimane dentro il bicchiere. Se invece la concavità è rivolta verso il basso, l’acqua cade dal bicchiere.

In termini più rigorosi, possiamo affermare che se l’ordinata del fuoco è maggiore dell’ordinata comune ai punti della direttrice, ovvero {d}, la parabola rivolge la propria concavità verso l’alto:

y_F > d \quad \Rightarrow \quad \text{concavita' verso l'alto}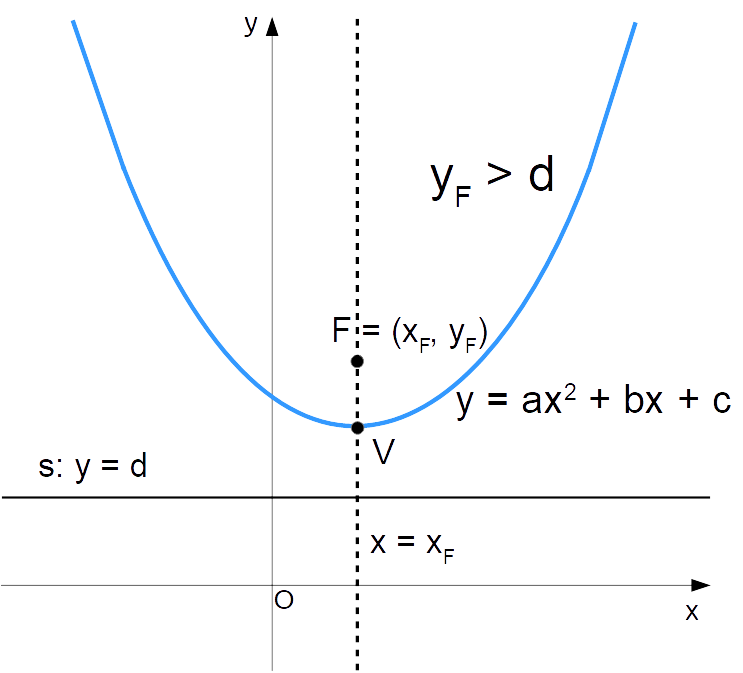

Se invece l’ordinata del fuoco è minore dell’ordinata {d} dei punti della direttrice, la parabola rivolge la propria concavità verso il basso:

y_F< d \quad \Rightarrow \quad \text{concavità verso il basso}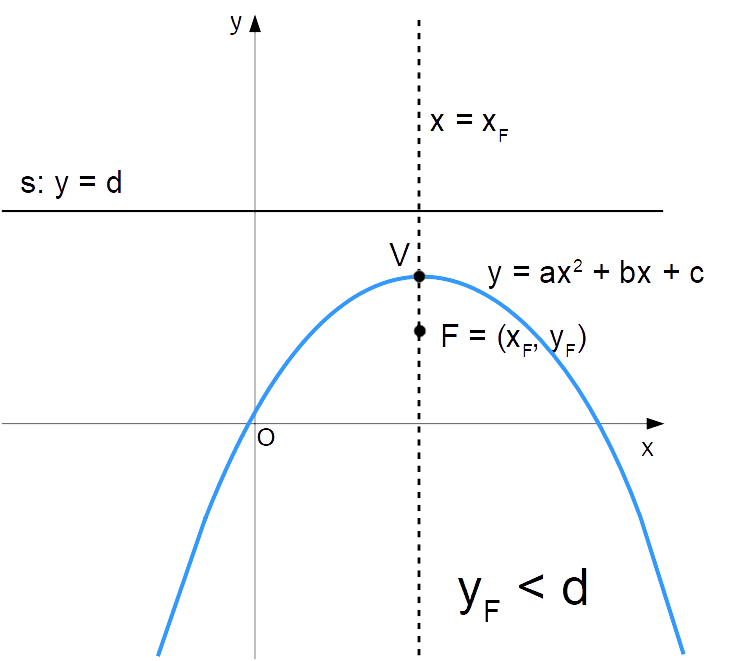

Tutto ciò è una diretta conseguenza della definizione della parabola come luogo geometrico. Provando a costruire una parabola posizionando in un modo o nell’altro il fuoco si troverà conferma di quanto sin qui affermato.

Ora, consideriamo separatamente i due casi. Tenendo conto delle formule per {y_F} e {d} in funzione dei coefficienti dell’equazione della parabola, nel caso di una parabola con concavità rivolta verso l’alto abbiamo:

y_F> d \quad \Rightarrow\quad  \dfrac{1-\Delta}{4a} > -\dfrac{1+ \Delta}{4a}

Sviluppiamo i calcoli relativamente a quest’ultima disequazione:

\begin{align*} &\dfrac{1-\Delta}{4a}+\dfrac{1+\Delta}{4a} > 0; \\ \\ & \dfrac{1-\cancel{\Delta} + 1 +\cancel{\Delta}}{4a}>0;\\ \\ &\dfrac{2}{4a}> 0 \quad \Rightarrow \quad \dfrac{1}{2a}>0 & \end{align*}

Ora, il termine {\dfrac{1}{2a}} sarà positivo, come richiesto dalla disequazione, soltanto se {a} è positivo. Di conseguenza, se una parabola con asse di simmetria verticale ha concavità rivolta verso l’alto il coefficiente {a} dell’equazione corrispondente alla parabola stessa è positivo.

Viceversa, vediamo cosa succede partendo dall’ipotesi {a>0}. Osserviamo intanto che per le ** si ha:

a=\dfrac{1}{2(y_F-d)}

Di conseguenza, se {a>0} dovrà essere necessariamente:

\begin{align*} &\dfrac{1}{2(y_F-d)}>0\end{align*}

e quindi:

y_F-d > 0 \quad \Rightarrow \quad y_F> d

Per cui se il coefficiente {a} è positivo l’ordinata del fuoco è necessariamente maggiore della distanza con segno {d} della direttrice rispetto all’asse {x}. Ovvero, se il coefficiente {a} è positivo il fuoco si trova necessariamente al di sopra della direttrice, e quindi la concavità della parabola è rivolta verso l’alto.

Abbiamo in conclusione dimostrato che se la concavità della parabola è rivolta verso l’alto allora {a>0}, ed inoltre che se {a>0} allora la concavità della parabola è rivolta verso l’alto. Pertanto, risulta dimostrato che {a>0} è sia condizione necessaria, sia condizione sufficiente affinché una parabola con asse di simmetria verticale abbia concavità rivolta verso l’alto.

Osservazione. Per condizione necessaria e sufficiente intendiamo ciò che serve e allo stesso tempo basta affinché una data affermazione risulti vera.
Nei termini propri della logica, dire che la proposizione {A} è condizione necessaria e sufficiente per la proposizione {B} equivale ad affermare l’equivalenza logica tra le due proposizioni, ovvero {A \iff B} (doppia implicazione).
Per dimostrare l’equivalenza logica tra le due proposizioni, occorre dimostrare le due implicazioni {A \Rightarrow B} (ovvero {A} condizione sufficiente per {B}) e {B \Rightarrow A} (ovvero {A} condizione necessaria per {B}).
Effettivamente, nel nostro caso per dimostrare che la condizione {a>0} è necessaria e sufficiente affinché la parabola rivolga la concavità verso l’alto, abbiamo dovuto dimostrare che la condizione {a>0} implica la concavità della parabola verso l’alto (quindi {A \Rightarrow B}) e viceversa che se la concavità della parabola è rivolta verso l’alto allora abbiamo come conseguenza la condizione {a > 0} (quindi {B \Rightarrow A}).
Ciò consente di affermare in definitiva che {a > 0} se e solo se la concavità della parabola è rivolta verso l’alto, sussistendo quindi l’equivalenza logica tra il dire che il coefficiente {a} è positivo e l’affermare che la parabola ha concavità rivolta verso l’alto.

Possiamo quindi affermare in conclusione quanto segue.

Una parabola con asse di simmetria verticale di equazione {y=ax^2+bx+c} ha concavità rivolta verso l’alto se e solo se {a>0}, ovvero se il coefficiente {a} è positivo.

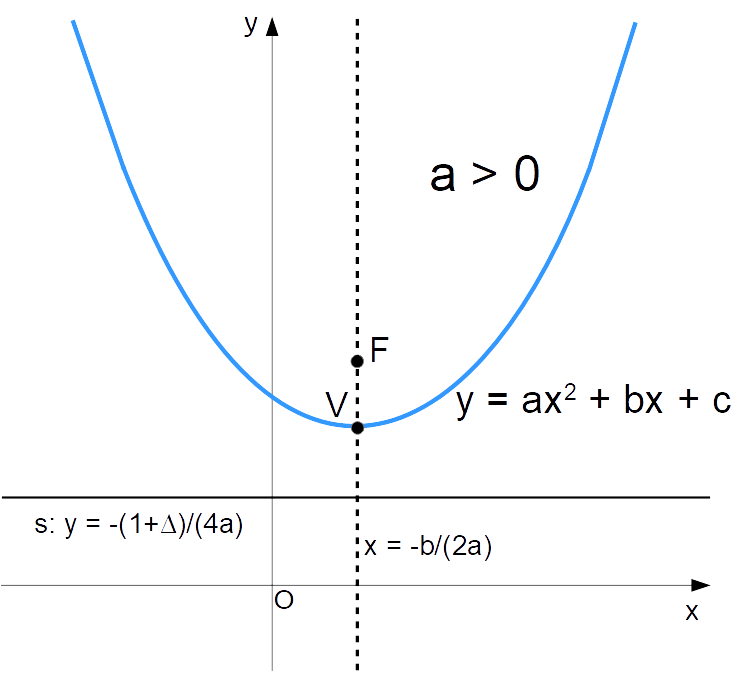
Considerando la disequazione {y< d} relativa al caso di concavità rivolta verso il basso e procedendo allo stesso modo si ha inoltre quanto segue:

\small \begin{align*} & y_F < d   \quad \Rightarrow \: \dfrac{1-\Delta}{4a}<-\dfrac{1+\Delta}{4a} \quad \Rightarrow \: \dfrac{2-\cancel{\Delta}+\cancel{\Delta}}{4a}<0 \quad \Rightarrow \:\dfrac{1}{2a}<0 \quad \Rightarrow \: a<0; \\ \\ & a<0\quad \Rightarrow \quad\dfrac{1}{2(y_F-d)}<0 \quad \Rightarrow \quad y_F-d < 0 \quad \Rightarrow \quad y_F < d \end{align*}

ovvero, rispettivamente, se l’ordinata del fuoco è minore della distanza con segno {d} allora il coefficiente {a} è negativo, e viceversa se {a} è negativo allora l’ordinata del fuoco è minore della distanza con segno {d}. Quindi vale in conclusione la seguente affermazione.

Una parabola con asse di simmetria verticale di equazione {y=ax^2+bx+c} ha concavità rivolta verso il basso se e solo se {a<0}, ovvero se il coefficiente {a} è negativo.

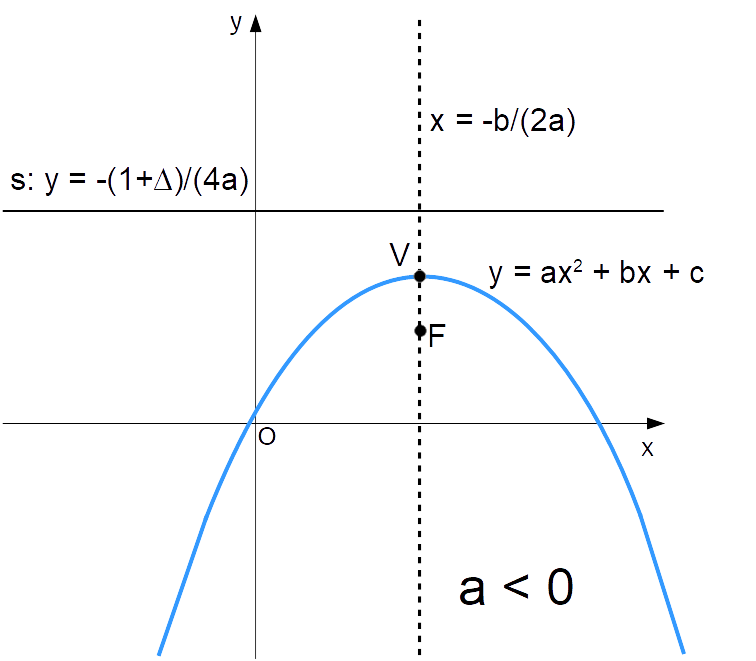
Esempio 3

Stabilire la concavità della parabola {\mathscr{P}_1} di equazione {y=-2x^2+3x+6} e della parabola {\mathscr{P}_2} di equazione {y=3x^2-4x-5}.

Entrambe le parabole hanno equazioni della forma {y=ax^2+bx+c} e quindi hanno asse di simmetria verticale.

La parabola {\mathscr{P}_1} ha coefficiente {a} negativo e pertanto ha la concavità rivolta verso il basso, mentre la parabola {\mathscr{P}_2} ha coefficiente {a} positivo e quindi ha la concavità rivolta verso l’alto.

Equazione di una parabola con asse di simmetria parallelo all’asse x

Veniamo ora al caso di una parabola con asse di simmetria parallelo all’asse x, ovvero con asse di simmetria orizzontale.

Una parabola con asse di simmetria orizzontale è caratterizzata da una direttrice parallela all’asse delle {y}, ovvero verticale. Ciò è conseguenza del fatto che in una parabola l’asse di simmetria è perpendicolare alla direttrice.

Consideriamo pertanto come direttrice {s} della parabola una retta verticale, ovvero una retta con equazione del tipo:

s: x = d

ovvero in forma implicita:

s:x-d=0

ove {d} è la distanza con segno tra la direttrice e l’asse delle {y}, e un punto {F=(x_F, y_F)} non appartenente ad {s} detto ancora fuoco della parabola.

Anche in questo caso la parabola si definisce come il luogo dei punti {P=(x,y)} del piano tali da essere equidistanti dal fuoco e dalla direttrice. Per cui le coordinate {x, y} di ciascun punto {P} della parabola dovranno essere tali da soddisfare l’uguaglianza:

d(P, s)=d(P,F)

ovvero, tenendo conto della formula della distanza punto-retta e della formula della distanza tra due punti:

\dfrac{|1 \cdot x+0\cdot y-d|}{\sqrt{1^2+0^2}}=\sqrt{(x_F-x)^2+(y_F-y)^2}

ossia:

|x-d|=\sqrt{(x_F-x)^2+(y_F-y)^2}

Osserviamo che per il primo membro abbiamo utilizzato la formula della distanza punto-retta tenendo conto dell’equazione in forma implicita {a_sx+b_sy+c_s=0} della retta direttrice, ovvero {s:x-d=0} con {a_s=1, b_s=0, c_s=-d}.

Eleviamo al quadrato entrambi i membri dell’equazione. Non serve alcuna condizione di concordanza né di realtà, poiché entrambi i membri sono positivi e poiché il radicando al secondo membro è una quantità sempre positiva, trattandosi di una somma di quadrati.

\begin{align*} &(x-d)^2=(x_F-x)^2+(y_F-y)^2;\\ \\ & \cancel{x^2}-2dx+d^2=x_F^2-2x_Fx+\cancel{x^2}+y_F^2-2y_Fy+y^2;\\ \\ & 2x_Fx-2dx=x_F^2+y_F^2-2y_Fy+y^2-d^2; \end{align*}

A questo punto riordiniamo i termini ed isoliamo la {x}:

\begin{align*} & x(2x_F-2d)=y^2-2y_Fy+x_F^2+y_F^2-d^2;\\ \\ & x[2(x_F-d)  ]=y^2-2y_Fy+x_F^2+y_F^2-d^2; \\ \\ &x=\dfrac{1}{2(x_F-d)}y^2+\dfrac{-2y_F}{2(x_F-d)}y+\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)};\\ \\ & x=\dfrac{1}{2(x_F-d)}y^2+\dfrac{-y_F}{x_F-d}y+ \dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)}\end{align*}

Ora, ponendo le seguenti sostituzioni:

a=\dfrac{1}{2(x_F-d)}, \qquad b=\dfrac{-y_F}{x_F-d}, \qquad c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)} \qquad (***)

si ha in conclusione l’equazione:

\boxed{x=ay^2+by+c, \qquad a \neq 0, \quad a,b,c \in \R} \qquad (2)

che rappresenta l’equazione di una parabola con direttrice verticale e quindi con asse di simmetria orizzontale, ovvero con asse di simmetria parallelo all’asse delle {x}.

Vediamo ora come scrivere l’equazione di una parabola con asse di simmetria orizzontale a partire dalle coordinate del fuoco e dalla distanza con segno {d} della direttrice rispetto all’asse {y}.

Esempio 4

Determinare l’equazione della parabola avente fuoco {F=(2,5)} e direttrice di equazione {s:x=-4}.

Poiché l’equazione della direttrice è una retta verticale, la parabola in esame è ad asse di simmetria orizzontale. Di conseguenza, l’equazione della parabola sarà della forma {x=ay^2+by+c}.

Tramite le ***, calcoliamo i coefficienti {a,b,c} dell’equazione della parabola:

\begin{align*} & a=\dfrac{1}{2(x_F-d)}=\dfrac{1}{2[2-(-4)]}=\dfrac{1}{12};\\ \\ &  b=\dfrac{-y_F}{x_F-d}=\dfrac{-5}{2-(-4)}=- \dfrac{5}{6} \\ \\ &  c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)}=\dfrac{2^2+5^2-(-4)^2}{2[2-(-4)]} =\dfrac{4+25-16}{12}= \dfrac{13}{12}\end{align*}

Così in conclusione l’equazione della parabola in esame è:

x=\dfrac{1}{12}y^2-\dfrac{5}{6}y+\dfrac{13}{12}

Come determinare le coordinate del fuoco, del vertice e l’equazione della direttrice di una parabola con asse orizzontale

Supponiamo che sia data l’equazione di una parabola con asse di simmetria orizzontale:

x=ay^2+by+c, \qquad a \neq 0

Vediamo come determinare le coordinate del fuoco, del vertice e l’equazione della direttrice della parabola. Il metodo che utilizzeremo è del tutto simile a quello già visto per una parabola con asse di simmetria verticale.

Partendo dalle ***, che per comodità riscriviamo:

a=\dfrac{1}{2(x_F-d)}, \qquad b=\dfrac{-y_F}{x_F-d}, \qquad c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)} \qquad (***)

impostiamo il seguente sistema, con l’obiettivo di ricavare le coordinate {x_F} ed {y_F} del fuoco e la distanza con segno {d} della direttrice rispetto all’asse {y}:

\begin{cases} a=\dfrac{1}{2(x_F-d)} \\ \\ b=\dfrac{-y_F}{x_F-d} \\ \\  c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)}   \end{cases}

Come nel caso precedente, l’idea è sempre quella di ricavare delle espressioni per {x_F} e {y_F} dalle prime due equazioni, sostituendole poi nella terza. In particolare, i passaggi sono del tutto simili a quelli già svolti nel caso di una parabola con asse di simmetria verticale, ma li riportiamo comunque per completezza.

\begin{align*} &\begin{cases} a=\dfrac{1}{2(x_F-d)} \quad \rightarrow \quad x_F-d=\dfrac{1}{2a} \quad \rightarrow \quad x_F=\dfrac{1}{2a}+d, \qquad x_F-d \neq 0 \\ \\ b=\dfrac{-y_F}{x_F-d} \quad \rightarrow \quad y_F=-b(x_F-d), \qquad x_F-d \neq 0 \\ \\  c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)}   \end{cases}\end{align*}

Osserviamo che la condizione {x_F-d \neq 0}, ovvero {x_F \neq d} è certamente soddisfatta poiché nella definizione di parabola come luogo geometrico il fuoco non appartiene alla direttrice.

Sostituiamo l’espressione ottenuta per {x_F} dalla prima equazione nella seconda equazione:

\begin{align*} &\begin{cases} x_F=\dfrac{1}{2a}+d  \\ \\  y_F=-b(x_F-d) \quad \rightarrow \quad y_F=-b\left( \dfrac{1}{2a}+\cancel{d}-\cancel{d}\right) \quad \rightarrow \quad \boxed{y_F=-\dfrac{b}{2a}}\\ \\  c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)}   \end{cases}\end{align*}

Ora grazie alle prime due equazioni disponiamo delle espressioni relative a {x_F} ed {y_F} nella sola funzione dei coefficienti dell’equazione della parabola e della distanza con segno {d}. Sostituiamo tali espressioni nella terza equazione, considerandola separatamente. L’obiettivo è ricavare un’espressione per {d}:

\begin{align*} &c=\dfrac{\left( \dfrac{1}{2a}+d\right)^2+\left( -\dfrac{b}{2a}\right)^2-d^2}{2\left( \dfrac{1}{2a}+\cancel{d}-\cancel{d}\right)};\\ \\ &c=\dfrac{\dfrac{1}{4a^2}+\dfrac{d}{a}+d^2+\dfrac{b^2}{4a^2}-d^2}{\dfrac{1}{a}};\\ \\ & c=\dfrac{1+4ad+\cancel{4a^2d^2}+b^2-\cancel{4a^2d^2}}{4a^{\cancel{2}}}\cdot \cancel{ a};\\ \\ & \dfrac{4ac-1-4ad-b^2}{\cancel{4a}}=0, \qquad a \neq 0 \\ \\ & 4ad=-1-b^2+4ac;\\ \\ & 4ad=-1-(b^2-4ac); \\ \\ & d=\dfrac{-1-\Delta}{4a}; \\ \\ & \boxed{d=-\dfrac{1+\Delta}{4a}} \end{align*}

Sostituendo poi l’espressione appena ottenuta per {d} nell’espressione per {x_F} relativa alla prima equazione a sistema:

\begin{align*} &x_F=\dfrac{1}{2a}+d=\dfrac{1}{2a}-\dfrac{1+\Delta}{4a}=\dfrac{2-1-\Delta}{4a} \\ \\ & \Rightarrow \quad \boxed{x_F=\dfrac{1-\Delta}{4a}}  \end{align*}

Infine, osserviamo che in una parabola con asse di simmetria orizzontale l’ordinata del fuoco e l’ordinata del vertice coincidono. Così, sostituendo la coordinata {y_F} del fuoco nell’equazione della parabola abbiamo per l’ordinata del vertice:

\begin{align*} &x_V=ay_F^2+by_F+c=a \left( -\dfrac{b}{2a}\right)^2+b\left( -\dfrac{b}{2a}\right)+c=\\ \\ & =\dfrac{ab^2}{4a^2}-\dfrac{b^2}{2a}+c=\dfrac{ab^2-2ab^2+4a^2c}{4a^2}=\dfrac{-ab^2+4a^2c}{4a^2}=\\ \\ & =\dfrac{\cancel{a}(-b^2+4ac)}{4a^{\cancel{2}}}=\dfrac{-(b^2-4ac)}{4a}=\dfrac{-\Delta}{4a}\\ \\ & \Rightarrow \quad \boxed{x_V=-\dfrac{\Delta}{4a}}\end{align*}

Possiamo riassumere i risultati sin qui ottenuti per le parabole ad asse di simmetria orizzontale come segue.

Il fuoco {F} di una parabola ad asse di simmetria orizzontale di equazione {x=ay^2+by+c} è dato da:{F=\left( \dfrac{1-\Delta}{4a}, -\dfrac{b}{2a}\right)}La distanza con segno {d} della direttrice rispetto all’asse {y} è invece data da:{d=-\dfrac{1+\Delta}{4a}}Di conseguenza, l’equazione della direttrice è:{s:x=-\dfrac{1+\Delta}{4a}}Infine, il vertice si calcola come:{V=\left(-\dfrac{\Delta}{4a}, -\dfrac{b}{2a} \right)}ove, in tutte le formule: {\Delta=b^2-4ac}.

Esempio 5

Determinare le coordinate del fuoco, del vertice e l’equazione della direttrice della parabola di equazione {x=2y^2+3y-7}.

L’equazione della parabola è della forma {x=ay^2+by+c}. Abbiamo quindi una parabola con asse di simmetria orizzontale, ovvero direttrice verticale. Equivalentemente, l’asse di simmetria della parabola è parallelo all’asse delle {x}.

Nel nostro caso l’equazione è:

x=2y^2+3y-7

e confrontandola con la forma generale abbiamo i coefficienti:

a=2, \qquad b=3, \qquad c=-7

Prima di applicare le formule, è conveniente calcolare il determinante {\Delta}:

\Delta = b^2-4ac=3^2-4\cdot2\cdot(-7)=9+56=65

Per il fuoco abbiamo:

\small \begin{align*} &F=(x_F,y_F)=\left( \dfrac{1-\Delta}{4a}, -\dfrac{b}{2a}\right)=\left(\dfrac{1-65}{4 \cdot 2} , -\dfrac{3}{2 \cdot 2}\right)=\left( -\dfrac{64}{8}, -\dfrac{3}{4}\right)=\left(-8,-\dfrac{3}{4}\right)\end{align*}

mentre per la distanza con segno {d} della direttrice rispetto all’asse {y}:

d=-\dfrac{1+\Delta}{4a}=-\dfrac{1+65}{4 \cdot 2}=-\dfrac{66}{8}=-\dfrac{33}{4}

Di conseguenza l’equazione della direttrice {s} è {x=d} ovvero:

s:x=-\dfrac{33}{4}

Infine per il vertice:

\begin{align*} &V=(x_V, y_V)=\left(-\dfrac{\Delta}{4a}, \overbrace{-\dfrac{b}{2a}}^{y_F} \right)= \left( -\dfrac{65}{4 \cdot 2}, -\dfrac{3}{4}\right)=\left( -\dfrac{65}8{, -\dfrac{3}{4}}\right)\end{align*}

Osserviamo che non è stato necessario calcolare l’ordinata del vertice, poiché questa nelle parabole con asse di simmetria orizzontale coincide con l’ordinata del fuoco. In caso di dubbi è comunque possibile eseguire per intero il calcolo.

Se non si ricordano le formule del vertice, infine, possiamo ottenere in alternativa l’ascissa del vertice sostituendo l’ordinata del fuoco nell’equazione della parabola:

\begin{align*} &x_V=ay_F^2+by_F+c=2 \cdot \left( -\dfrac{3}{4}\right)^2+3 \cdot \left( -\dfrac{3}4{}\right)-7=\\ \\ & =2\cdot\dfrac{9}{16}-\dfrac{9}{4}-7=\dfrac{9-18-56}{8}=-\dfrac{65}{8}\end{align*}

Quindi ritroviamo correttamente anche in questo modo l’ascissa del vertice.

Concavità delle parabole con asse di simmetria orizzontale

Come nel caso delle parabole con asse di simmetria verticale, anche nelle parabole con asse di simmetria orizzontale la concavità dipende dalla posizione del fuoco della parabola rispetto alla sua direttrice.

In una parabola con asse di simmetria orizzontale, la direttrice, perpendicolare ad esso, è verticale. Di conseguenza, per la posizione del fuoco rispetto alla direttrice potremo avere due distinti casi:

• ascissa del fuoco maggiore della distanza con segno {d} della direttrice rispetto all’asse {y}, ovvero {x_F > d}. In tal caso la parabola rivolge la sua concavità verso la direzione positiva dell’asse delle {x};
• ascissa del fuoco minore della distanza con segno {d} della direttrice rispetto all’asse {y}, ovvero {x_F < d}. In tal caso la parabola rivolge la sua concavità verso la direzione negativa dell’asse delle {x}.

I due casi equivalgono ad avere rispettivamente il fuoco a destra della direttrice oppure a sinistra della direttrice, e sono diretta conseguenza della definizione di parabola come luogo geometrico.

Per ciascuno dei due distinti casi abbiamo, tenendo conto delle formule delle coordinate del fuoco e della quantità {d} relative ad una parabola ad asse orizzontale:

\begin{align*} &x_F > d \quad \Rightarrow \quad  \dfrac{1-\Delta}{4a} > -\dfrac{1+\Delta}{4a} \quad &&\Rightarrow   \dfrac{1-\cancel{\Delta}+1+\cancel{\Delta}}{4a} > 0  \\ \\ & &&\Rightarrow\dfrac{2}{4a}> 0  \\ \\ & && \Rightarrow \dfrac{1}{2a}>0 \iff a > 0; \\ \\ & x_F< d \quad \Rightarrow \quad \dfrac{1-\Delta}{4a} < -\dfrac{1+\Delta}{4a} &&\Rightarrow  \dfrac{1-\cancel{\Delta}+1+\cancel{\Delta}}{4a}<0 \\ \\ &  && \Rightarrow \dfrac{1}{2a}< 0 \iff a < 0 \end{align*}

Quindi se una parabola con asse orizzontale rivolge la propria concavità verso la direzione positiva dell’asse delle {x} risulta {a>0}, mentre se una parabola con asse orizzontale rivolge la propria concavità verso la direzione negativa dell’asse delle {x} risulta {a<0}.

Viceversa, utilizzando le *** relativamente al coefficiente {a} otteniamo rispettivamente:

\begin{align*} &a> 0 \quad \Rightarrow \quad  \dfrac{1}{2(x_F-d)}>0 \quad \Rightarrow \quad x_F-d > 0 \quad \Rightarrow \: x_F>d; \\ \\ & a< 0 \quad \Rightarrow \quad \dfrac{1}{2(x_F-d)}<0 \quad \Rightarrow \quad x_F-d < 0 \quad \Rightarrow \: x_F < d \end{align*}

Di conseguenza, se {a>0} una parabola con asse di simmetria orizzontale rivolge la propria concavità verso la direzione positiva dell’asse delle {x}, mentre se {a<0} una parabola con asse di simmetria orizzontale rivolge la propria concavità verso la direzione negativa dell’asse delle {x}.

Così in conclusione possiamo affermare quanto segue.

Una parabola con asse di simmetria orizzontale rivolge la propria concavità verso la direzione positiva dell’asse delle {x} se e solo se {a>0}, mentre rivolge la propria concavità verso la direzione negativa dell’asse delle {x} se e solo se {a < 0}.

I due casi corrispondono alle seguenti figure:

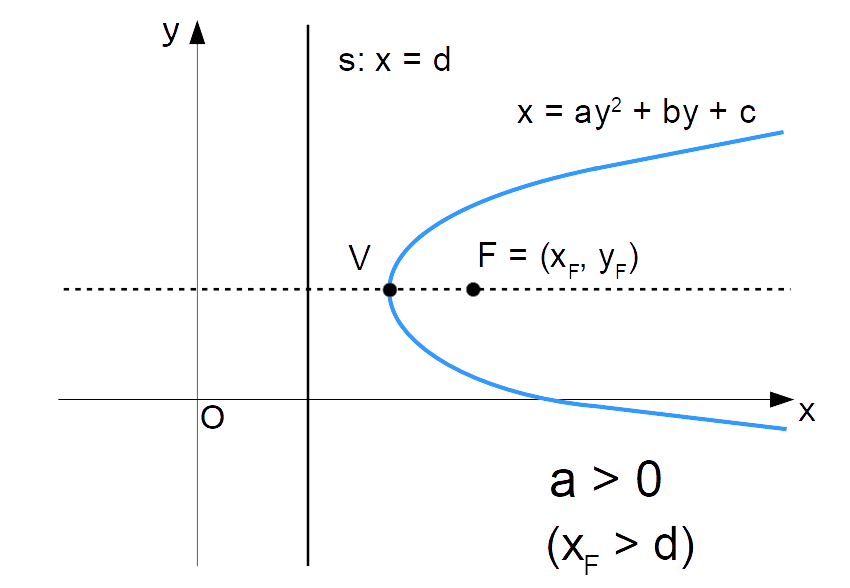
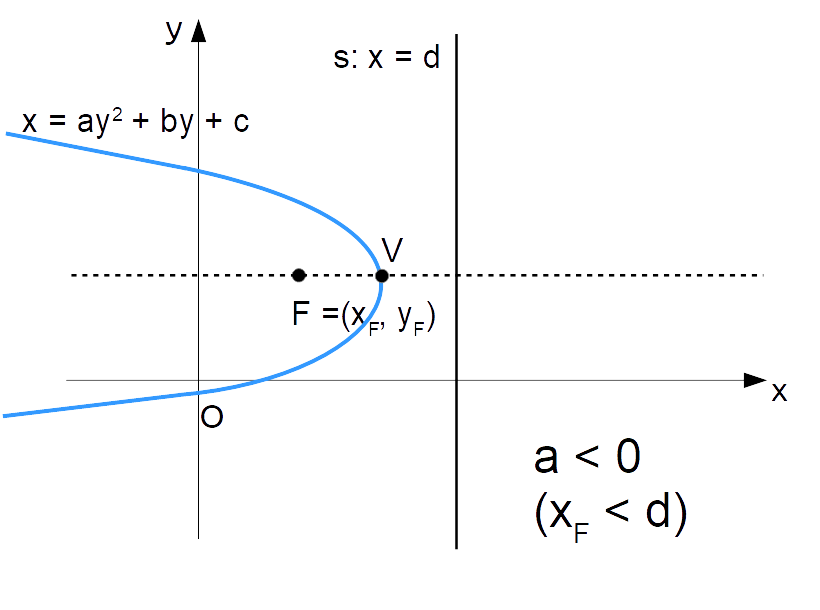
Esempio 6

Stabilire la concavità della parabola {\mathscr{P}_1} di equazione {x=-3y^2+3y+5} e della parabola {\mathscr{P}_2} di equazione {x=4y^2-4y-8}.

Entrambe le parabole hanno equazioni della forma {x=ay^2+by+c} ed hanno quindi asse di simmetria orizzontale.

La parabola {\mathscr{P}_1} ha coefficiente {a} negativo e pertanto ha la concavità rivolta verso la direzione negativa dell’asse delle {x}, mentre la parabola {\mathscr{P}_2} ha coefficiente {a} positivo e quindi ha la concavità rivolta verso la direzione positiva dell’asse delle {x}.

Conclusioni

Per questa lezione introduttiva sulla parabola è tutto. Abbiamo in particolare visto come scrivere l’equazione di una parabola in entrambi i casi di asse di simmetria verticale ed orizzontale. Precisiamo comunque che le parabole con asse di simmetria verticale sono quelle più ricorrenti. Queste infatti vengono utilizzate per risolvere le disequazioni di secondo grado. Tuttavia, è comunque importante sapersi destreggiare in entrambi i casi.

Nelle prossime lezioni torneremo a considerare le equazioni di parabole con asse di simmetria verticale ed orizzontale, esaminando separatamente ciascun caso con un taglio più mirato alle formule e alle loro applicazioni, riproponendo le dimostrazioni soltanto alla fine di ciascuna lezione. Dopo l’infarinatura generale di questa lezione, sarà così possibile approfondire ed assorbire meglio ciascun singolo argomento. In una successiva lezione ci occuperemo poi del problema della parabola con vertice nell’origine.

Nella lezione ancora successiva ci occuperemo invece delle intersezioni tra rette e parabole, per poi proseguire con il problema delle rette tangenti ad una parabola fino allo studio delle condizioni per determinare le equazioni di una parabola. La sequenza degli argomenti, come avrete notato, è molto simile a quella già adottata per la circonferenza.

Un saluto a tutti voi e buon proseguimento con SìMatematica!