Segmento parabolico (teorema di Archimede)

 - 

Parabola (scuole superiori)

Il segmento parabolico è un’area delimitata da un tratto di una parabola (arco di parabola) e da una retta perpendicolare o in generale non parallela all’asse della parabola stessa, e tale da intersecare la parabola in almeno due suoi punti. Il segmento parabolico è dunque una particolare regione del piano la cui area dipende dalla parabola in esame e dalla retta considerata.

Nella lezione vedremo come determinare l’area di un dato segmento parabolico considerando la differenza tra l’area di un opportuno rettangolo e l’area “sottesa” dalla parabola nel tratto considerato. Tuttavia, mentre è ovvio come determinare l’area di un rettangolo, meno ovvio è invece determinare l’area “sottesa” dalla parabola nel dato tratto. Tuttavia, mostreremo come è possibile valutare tale area approssimandola con un numero “grandissimo” di rettangolini uniti tra loro. In tal modo, la somma dei rettangolini sarà uguale alla somma dell’area “sottesa” dall’arco di parabola. Sarà quindi possibile a tal punto calcolare l’area del segmento parabolico in esame.

Il teorema al quale arriveremo e che ci permetterà di calcolare l’area di un dato segmento parabolico prende il nome di teorema di Archimede.

Ma vediamo subito nel dettaglio la definizione di segmento parabolico, considerando il caso di una parabola con asse verticale.

Importante. Nel seguito introdurremo gradualmente il teorema di Archimede partendo dalla dimostrazione. Tuttavia chi lo desidera può passare subito all’enunciato ed ai relativi esempi. Sarà comunque possibile studiare la dimostrazione in un secondo momento.
Raccomandiamo comunque di leggere per intero la lezione, tuttalpiù senza concentrarvi troppo sulla dimostrazione del teorema se questa non è richiesta dal vostro insegnante.

Segmento parabolico

Consideriamo una parabola {\mathscr{P}} con asse verticale, e quindi con equazione della forma:

\mathscr{P}:y=ax^2+bx+c, \qquad a,b,c \in \R

Supponiamo inoltre che la parabola abbia concavità rivolta verso l’alto, ovvero che valga la condizione {a > 0}.

Consideriamo inoltre una retta {r} orizzontale, quindi perpendicolare all’asse della parabola, ed avente in generale equazione:

r:y=k, \qquad k \in \R

Inoltre, indicando il vertice della parabola con {V=\left( x_V, y_V\right)}, poiché la parabola rivolge la propria concavità verso l’alto dovrà essere:

k > y_V

ovvero la retta {r} dovrà trovarsi al di sopra del vertice della parabola {\mathscr{P}}.

Sotto tali ipotesi, la retta {r} intersecherà la parabola necessariamente in due punti distinti {A} ed {A'} (vedi: intersezioni di una parabola con una retta).

Infatti, il sistema che consente di determinare i punti di intersezione tra la parabola {\mathscr{P}} e la retta {r} è dato da:

\begin{cases} y=ax^2+bx+c \\ \\ y=k\end{cases}

Sostituendo nella prima equazione ad {y} la quantità {k} si ottiene l’equazione risolvente del sistema:

ax^2+bx+c-k=0

Il determinante di tale equazione è dato da:

\Delta = b^2-4 \cdot a \cdot (c-k)=b^2-4ac+4ak

La condizione {\Delta > 0}, per la quale la retta e la parabola hanno due punti di intersezione, diviene quindi:

b^2-4ac+4ak > 0 

ovvero (l’ipotesi {a > 0} ci indica di mantenere il verso del simbolo di disuguaglianza, vedi disequazioni):

4ak > -b^2+4ac \quad \Rightarrow \quad k > \dfrac{-b^2+4ac}{4a}

e quindi:

k > \dfrac{-(b^2-4ac)}{4a} \quad \Rightarrow \quad k > -\dfrac{\Delta}{4a}

Ma poiché la quantità {-\dfrac{\Delta}{4a}} è uguale all’ordinata del vertice di una parabola con asse verticale, ritroviamo in conclusione la condizione:

k> y_V

che è quindi confermata essere la condizione per la quale la parabola {\mathscr{P}} presenta due punti di intersezione con la retta {r}.

Così, valendo tale condizione, l’arco di parabola compreso tra i due punti {H'} e {H} (vedi figura a seguire) individua con la retta {r} la regione del piano {S}, che rappresenta il segmento parabolico relativo alla parabola {\mathscr{P}} e corrispondente alla retta {r}.

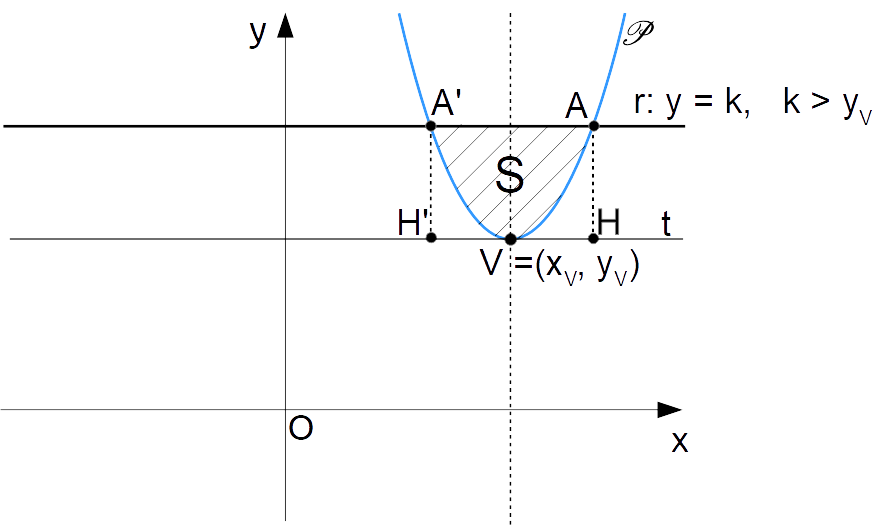
Osserviamo che i punti {H'} e {H} sono le proiezioni dei punti {A'} ed {A} sulla retta {t}, retta che è parallela ad {r} e tangente alla parabola.

Teorema di Archimede (dimostrazione ed enunciato)

Ora, il caso più generale di una parabola con vertice arbitrario richiede delle considerazioni un po’ complicate per poter arrivare al teorema di Archimede. Quindi, per semplicità conviene piuttosto considerare una parabola con vertice nell’origine degli assi:

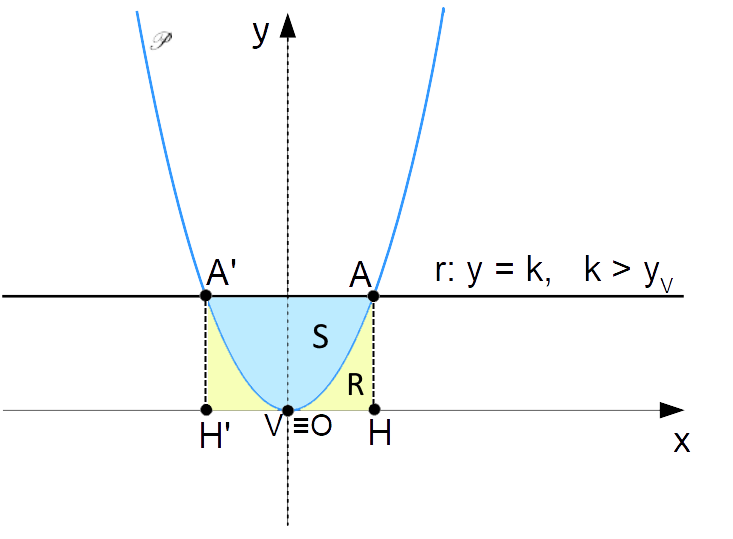
Ciò non è restrittivo, poiché è sempre possibile ricondursi dal caso di una parabola con vertice generico al caso di una parabola con vertice nell’origine mediante un’opportuna traslazione. Per cui le considerazioni che faremo nel seguito relativamente ad una parabola con asse verticale e vertice nell’origine saranno valide anche per una parabola avente per vertice un punto arbitrario.

Sotto tale ipotesi, ci ritroviamo più semplicemente con l’equazione della parabola {\mathscr{P}} con vertice nell’origine, esprimibile nella forma:

\mathscr{P}: y= ax^2, \qquad a \in \R

Osserviamo che in questo caso i punti {H'} e {H} sono le proiezioni dei punti {A'} e {A} sull’asse {x}. Infatti, la retta {t} parallela ad {r} e tangente alla parabola adesso coincide proprio con l’asse {x}.

Ora, l’area {S} del segmento parabolico si ottiene come differenza tra l’area del rettangolo {A'AHH'} e l’area {R} sottesa dalla parabola nel tratto considerato. Osserviamo che l’area {R} è data da tutta la zona in giallo. Abbiamo quindi:

S = \overline{A'A} \cdot \overline{A'H'} - R

Calcolare l’area del rettangolo {A'AHH'} non è complicato. Infatti, le coordinate dei punti {H'} e {H} sono della forma, rispettivamente:

H'=(-z, 0); \qquad H=(z,0)

Osserviamo che le ascisse dei punti {H} e {H'} sono uguali in valore assoluto poiché la parabola è simmetrica rispetto all’asse {y}.

Proseguendo, le ordinate dei punti {A'} e {A} sono date dalle valutazioni della funzione {y=ax^2} che rappresenta la parabola {\mathscr{P}} relativamente alle ascisse dei punti {H'} e {H}:

y_{A'}=a(-z)^2=az^2; \qquad y_A=az^2

Le ascisse dei punti {A'} ed {A} sono invece uguali rispettivamente alle ascisse dei punti {H'} e {H} (vedi precedente figura). Così abbiamo:

A'=(-z, az^2); \qquad A=(z, az^2)

Da ciò segue per le misure della base e dell’altezza del rettangolo {A'AHH'} (vedi formula della distanza tra due punti nel piano):

\small \begin{align*}& \overline{A'A}=\sqrt{(x_A-x_{A'})^2+(y_A-y_{A'})^2}=\sqrt{(z+z)^2+(az^2-az^2)^2}=2|z|=2z;  \\ \\ & \overline{A'H'} = \sqrt{(x_{H'}-x_{A'})^2+(y_{H'}-y_{A'})^2}=\sqrt{(-z+z)^2+(0-az^2)^2}=|a|z^2=az^2\end{align*}

Osserviamo che in entrambe le espressioni ottenute abbiamo eliminato il simbolo di modulo poiché una lunghezza è per definizione positiva.

A questo punto, per l’area del rettangolo abbiamo:

 \overline{A'A} \cdot \overline{A'H'}=2z \cdot az^2=2az^3

Per il calcolo dell’area della regione di piano {R} il discorso è invece meno diretto. L’idea è in particolare quella di utilizzare un metodo approssimato, consistente nel suddividere la regione {R} in {n} rettangolini, con {n} numero naturale “sufficientemente grande”. Intuitivamente, infatti, un numero adeguato di rettangolini con base “sufficientemente piccola” e con adeguata altezza affiancati tra loro è in grado di approssimare la regione {R} (vedi figura a seguire).

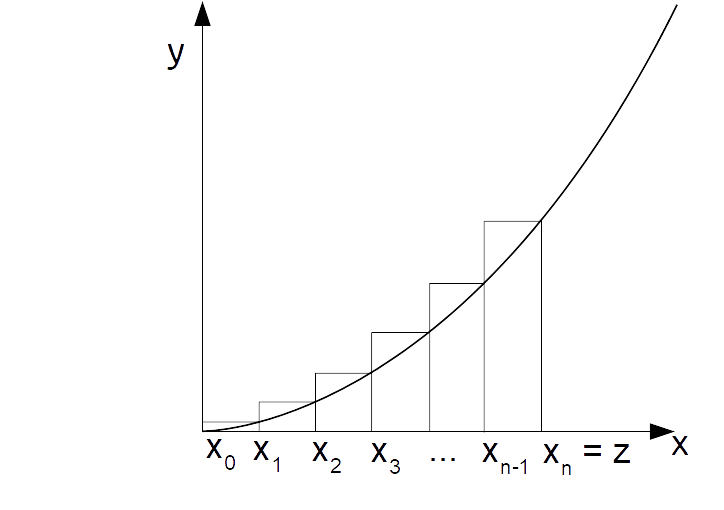
Nella figura consideriamo la sola regione di area {\dfrac{R}{2}}. Tuttavia, per valutare l’area di{R} basterà semplicemente moltiplicare per {2}. Infatti, la parabola in esame è simmetrica rispetto all’asse {y}.

Ora, tutti gli {n} rettangolini hanno base avente misura {\dfrac{z}{n}}, e ad essi corrispondono {n+1} punti aventi ascisse:

\small x_0=0, \quad x_1=\dfrac{z}{n}, \quad x_2=\dfrac{2z}{n}, \quad \dots ,\quad x_{n-1}=\dfrac{(n-1)z}{n}, \quad x_n=\dfrac{nz}{n}=z

Le corrispondenti ordinate sono date da (ricordiamo che stiamo considerando la parabola {\mathscr{P}: y= ax^2}):

\small y_0=0, \quad y_1=a\dfrac{z^2}{n^2}, \quad y_2=a\cdot\dfrac{4z^2}{n^2}, \quad \dots \quad y_{n-1}=a\dfrac{(n-1)^2z^2}{n^2}, \qquad y_n=az^2

Le espressioni appena scritte per le ordinate rappresentano le misure delle altezze relative a ciascun rettangolino (con l’eccezione di {y_0=0}). Così, l’area della regione {\dfrac{R}{2}} potrà essere approssimata dalla somma delle aree dei rettangolini. E ciascuna di tali aree sarà data dal prodotto della misura della base, uguale a {\dfrac{z}{n}} per ogni rettangolino, per l’altezza corrispondente a ciascun rettangolino. Abbiamo quindi:

\begin{align*}  \dfrac{R}{2} & \approx \dfrac{z}{n}\cdot a \cdot\dfrac{z^2}{n^2}+\dfrac{z}{n} \cdot a \cdot \dfrac{4z^2}{n^2}+\dots + \dfrac{z}{n} \cdot a \cdot \dfrac{(n-1)^2 z^2}{n^2} +\dfrac{z}{n} \cdot  a z^2=\\ \\ & =\dfrac{az^3}{n^3}+\dfrac{4az^3}{n^3}+\dots + (n-1)^2\cdot\dfrac{az^3}{n^3}+\dfrac{az^3}{n} \cdot \underbrace{\dfrac{n^2}{n^2}}_{1} = \\ \\ & =\dfrac{az^3}{n^3}+\dfrac{4az^3}{n^3}+\dots+(n-1)^2 \cdot \dfrac{az^3}{n^3}+n^2 \cdot\dfrac{az^3}{n^3}=\end{align*}

A questo punto, avendo moltiplicato l’ultimo termine nella somma per {\dfrac{n^2}{n^2}} (quantità uguale a 1) è possibile raccogliere tutti i termini per {\dfrac{az^3}{n^3}}. Proseguendo i passaggi si ha quindi:

\begin{align*} &=\dfrac{az^3}{n^3} \left[ \underbrace{1+4+\dots + (n-1)^2+n^2}_{\substack{\text{somma dei quadrati}  \\ \text{ dei primi n numeri  naturali}}}\right]\end{align*}

Ora, la somma dei quadrati dei primi {n} numeri naturali si dimostra essere uguale a {\dfrac{n^3}{3}+\dfrac{n^2}{2}+\dfrac{n}{6}}. Per cui abbiamo:

\begin{align*} & \dfrac{R}{2} \approx \dfrac{az^3}{n^3} \left( \dfrac{n^3}{3}+\dfrac{n^2}{2}+\dfrac{n}{6}\right)=az^3 \left( \dfrac{1}{3}+\dfrac{1}{2n}+\dfrac{1}{6n^2}\right) \end{align*}

Abbiamo così ottenuto un’approssimazione per la metà dell’area della regione {R}. E tale approssimazione migliorerà necessariamente all’aumentare del numero {n} di rettangolini considerato. In particolare, per {n} “molto grande”, i termini con denominatore in funzione di {n} nella somma entro le parentesi tonde possono essere considerati nulli. Così per {n} “grandissimo” (ovvero che tende ad infinito) trascurando i termini con lettere {n} al denominatore abbiamo:

\dfrac{R}{2}=\dfrac{1}{3}az^3 \qquad (\underbrace{n \rightarrow \infty}_{ \substack{\text{n che tende} \\ \\ \text{a infinito}}})

E quindi, evidentemente, per l’area della regione {R}:

R=\dfrac{2}{3}az^3

Osservazione. In modo molto intuitivo e non rigoroso, per convincersi che una quantità del tipo {\dfrac{1}{n}} si annulli per {n} infinitamente grande, basta una semplice calcolatrice. Si potrà notare infatti che aumentando il numero {n} al denominatore la frazione {\dfrac{1}{n}} diventerà sempre più prossima a zero.
Una trattazione rigorosa del calcolo infinitesimale verrà fornita in successive lezioni.

Ma a questo punto, l’area della regione {S} è finalmente esprimibile come differenza tra l’area del rettangolo {A'AHH'} e l’area della regione {R}:

S= \overline{A'A} \cdot \overline{A'H'} - \dfrac{2}{3}az^3=2az^3-\dfrac{2}{3}az^3=\left( 2-\dfrac{2}{3}\right)az^3=\dfrac{4}{3}az^3

Per cui abbiamo:

S=\dfrac{4}{3}az^3

Ora, ricordiamo che dai precedenti passaggi si ha:

\small \begin{align*}& \overline{A'A}=2z; \qquad  \overline{A'H'} =az^2\end{align*}

ed osserviamo che per l’espressione di {S} vale la scomposizione:

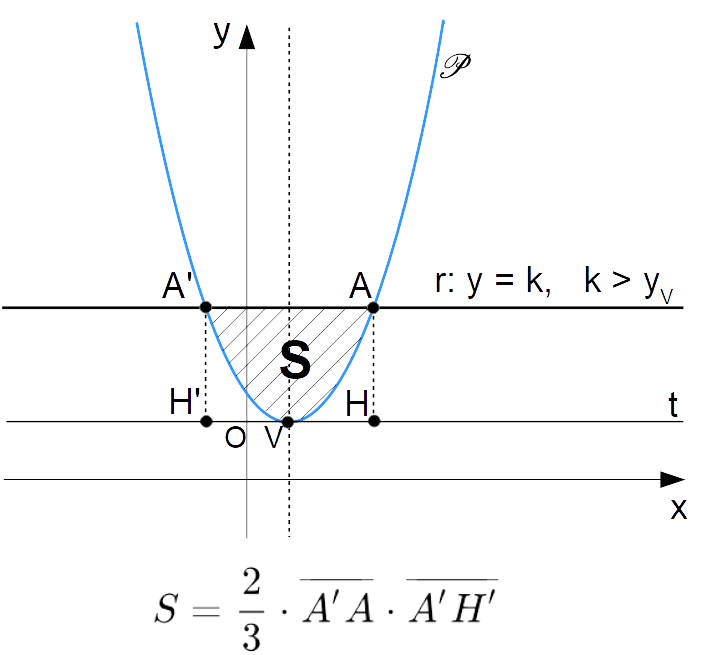
S=\dfrac{4}{3}az^3=\dfrac{2}{3} \cdot \underbrace{2z}_{\overline{A'A}} \cdot \underbrace{az^2}_{\overline{A'H'}}

Quindi in conclusione l’area della regione {S} è esprimibile in funzione dell’area del rettangolo {A'AHH'}, e ciò costituisce il teorema di Archimede:

\boxed{S=\dfrac{2}{3} \cdot  \overline{A'A} \cdot \overline{A'H'}}

A questo punto, ricordiamo ancora che una parabola con vertice generico può comunque essere ricondotta ad una parabola con vertice nell’origine mediante un’opportuna traslazione. Per cui, il teorema di Archimede è in generale valido per una parabola avente per vertice un punto qualsiasi.

Enunciato del teorema di Archimede (come calcolare l’area di un segmento parabolico)

Teorema di Archimede (nel caso specifico di una parabola con asse verticale e retta orizzontale, vertice qualunque).
Supponiamo che una certa retta {r:y=k, \: k \in \R} (orizzontale) sia tale da avere due punti di intersezione con una parabola {\mathscr{P}} avente asse verticale, ovvero valga la condizione {k > y_V}, con {y_V} ordinata del vertice della parabola. Allora, l’area {S} del segmento parabolico individuato dalla retta {r} sulla parabola {\mathscr{P}} è uguale ai {\dfrac{2}{3}} dell’area del rettangolo {A'AHH'}, ovvero il rettangolo avente come vertici i due punti di intersezione tra la parabola e la retta e le proiezioni di tali punti sulla retta {t} parallela ad {r} e tangente alla parabola.

Osservazione. Il teorema di Archimede è in generale valido anche nel caso in cui la retta {r} non sia orizzontale (ma comunque risulti non parallela all’asse della parabola e continui a presentare due punti di intersezione con la parabola stessa). In tal caso, due vertici del rettangolo sono sempre dati dai punti di intersezione della parabola {\mathscr{P}} con la retta {r}, mentre gli altri due vertici sono dati dalle proiezioni di tali punti di intersezione sulla retta {t} parallela a {r} e tangente alla parabola.
In questo caso, non ha ovviamente più senso porre la condizione {k > y_V}, poiché {r} non è più orizzontale.

Alla luce di quest’ultima osservazione, la seguente figura riassume l’enunciato del teorema di Archimede nella sua forma generale:

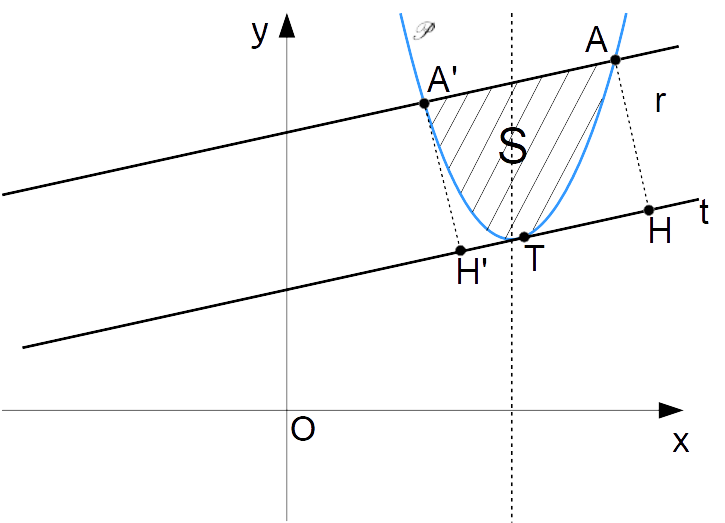
Se dunque la retta {r} presenta due punti di intersezione con la parabola {\mathscr{P}} (come nel caso in figura), si ha ancora:

\boxed{S=\dfrac{2}{3} \cdot  \overline{A'A} \cdot \overline{A'H'}}

Vediamo a questo punto degli esempi sull’utilizzo del teorema di Archimede, relativi a come calcolare l’area di un segmento parabolico.

Esempi (come calcolare l’area di un segmento parabolico)

Esempio 1

Calcolare l’area {S} del segmento parabolico relativo alla parabola {\mathscr{P}:y=x^2-4x+4} e individuato sulla parabola stessa dalla retta {r:y=4}.

Cominciamo rappresentando la parabola e la retta nel piano cartesiano. Per disegnare la parabola è utile calcolare le coordinate del suo vertice:

V=\left( -\dfrac{b}{2a}, -\dfrac{\Delta}{4a}\right)=\left( -\dfrac{-4}{2}, -\dfrac{16-16}{4}\right)=(2,0)

Osserviamo inoltre che poiché il coefficiente {a} è positivo la parabola rivolge la propria concavità verso l’alto.

Infine, per la forma della sua equazione la parabola è ad asse verticale. La retta {r} è invece orizzontale.

Vale la seguente rappresentazione:

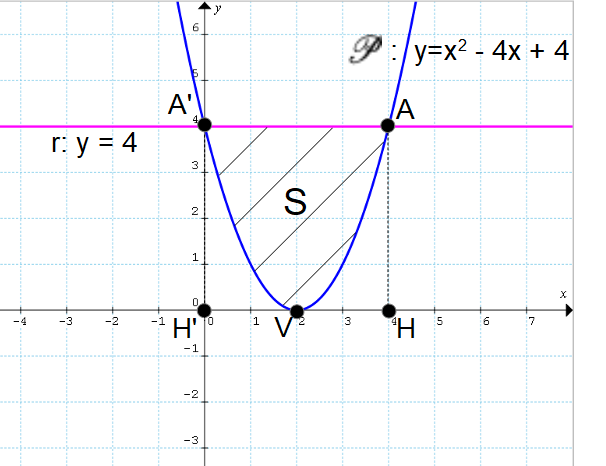
Come sappiamo dal teorema di Archimede, l’area del segmento parabolico {S} è uguale ai {\dfrac{2}{3}} dell’area del rettangolo {A'AHH'}. Ma per poter calcolare l’area di tale rettangolo è prima di tutto necessario ricavare le coordinate dei punti {A', A, H', H}.

I punti {A'} e {A} sono i punti di intersezione tra la parabola {\mathscr{P}} e la retta {r}. Di conseguenza, le ascisse dei punti {A'} ed {A} si ottengono risolvendo il seguente sistema:

\begin{cases} \mathscr{P}:y=x^2-4x+4 \\ \\ r:y=4 \end{cases}

Abbiamo, procedendo per sostituzione:

\begin{align*} &4=x^2-4x+4 ;\\ \\ &x^2-4x=0; \\ \\ & x(x-4)=0 \quad \Rightarrow \quad x=0 \quad \vee \quad x=4\end{align*}

Così il punto {A'} ha ascissa {0} mentre il punto {A} ha ascissa {4}. Infine, entrambi i punti hanno ordinata {4}, e pertanto possiamo scrivere:

A'=(0,4); \qquad A=(4,4)

Ora, i punti {H'} e {H} hanno la stessa ordinata del vertice. Infatti, tali punti sono le proiezioni rispettivamente di {A'} e {A} sulla retta tangente alla parabola e parallela ad {r} (che in questo caso è la retta orizzontale passante per il vertice, qui coincidente con l’asse {x}). Inoltre, tali punti hanno le stesse ascisse dei punti {A'} ed {A}. Abbiamo quindi:

H'=(0,0); \qquad H=(4,0)

Disponendo delle coordinate dei punti {A', A, H, H'} possiamo calcolare l’area del rettangolo {A'AHH'} (in questo caso è un quadrato di lato avente misura {4}) e quindi del segmento parabolico {S}:

S=\dfrac{2}{3} \cdot \overline{A'A} \cdot \overline{A'H}=\dfrac{2}{3} \cdot 4 \cdot 4=\dfrac{32}{3}

Abbiamo così visto come calcolare l’area del segmento parabolico dato.

Esempio 2

Calcolare l’area {S} del segmento parabolico relativo alla parabola {\mathscr{P}: y= -2x^2+6x+4} e individuato sulla parabola stessa dalla retta {r: y=x-3}.

Per maggiore chiarezza proponiamo il metodo risolutivo più lungo, basato sul calcolare le coordinate di tutti e quattro i vertici del rettangolo {A'AHH'}. A nostro parere infatti un tale metodo costituisce la strada più diretta per l’applicazione delle nozioni teoriche sin qui viste. Mostreremo poi come risparmiare diversi calcoli nell’esempio successivo, mediante l’utilizzo della formula della distanza punto-retta.

Cominciamo rappresentando la parabola {\mathscr{P}} e la retta {r} sul piano cartesiano.

Per la parabola, calcoliamo come al solito le coordinate del vertice:

V=\left( -\dfrac{b}{2a}, -\dfrac{\Delta}{4a}\right)=\left( -\dfrac{6}{-4}, -\dfrac{68}{-8}\right)=\left( \dfrac{3}{2}, \dfrac{17}{2}\right)

Osserviamo inoltre che la parabola ha coefficiente {a} negativo e rivolge quindi la propria concavità verso il basso. Questa ha poi asse verticale.

Per la retta, osserviamo che l’equazione data è della forma {y=mx+q} (forma esplicita), avendo in questo caso {m=1} e {q=-3}. La retta forma quindi un angolo di {45^{\circ}} con l’orizzontale ed ha ordinata all’origine uguale a {-3}.

Ora, per stabilire la posizione reciproca tra la parabola e la retta determiniamo i relativi punti di intersezione:

\begin{cases} \mathscr{P}: y= -2x^2+6x+4 \\ \\  r: y=x-3 \end{cases}

Procedendo per sostituzione si ha:

\begin{align*} &x-3=-2x^2+6x+4; \\ \\ & 2x^2-5x-7=0;\\ \\ & x_{1,2}=\dfrac{5 \pm \sqrt{25+56}}{4}=\dfrac{5 \pm 9}{4}=\begin{cases} \dfrac{7}{2} \\ \\ -1\end{cases}\end{align*}

Abbiamo in questo modo ottenuto le ascisse dei punti di intersezione. Per le ordinate, basta sostituire i valori appena calcolati nell’equazione {y=x-3} a sistema. Si ha così per i punti di intersezione cercati:

A=\left( \dfrac{7}{2}, \dfrac{7}{2}-3\right)=\left( \dfrac{7}{2}, \dfrac{1}{2}\right); \qquad A'=\left( -1, -1-3\right)=(-1,-4)

Possiamo quindi rappresentare la parabola {\mathscr{P}} e la retta {r} sul piano cartesiano:

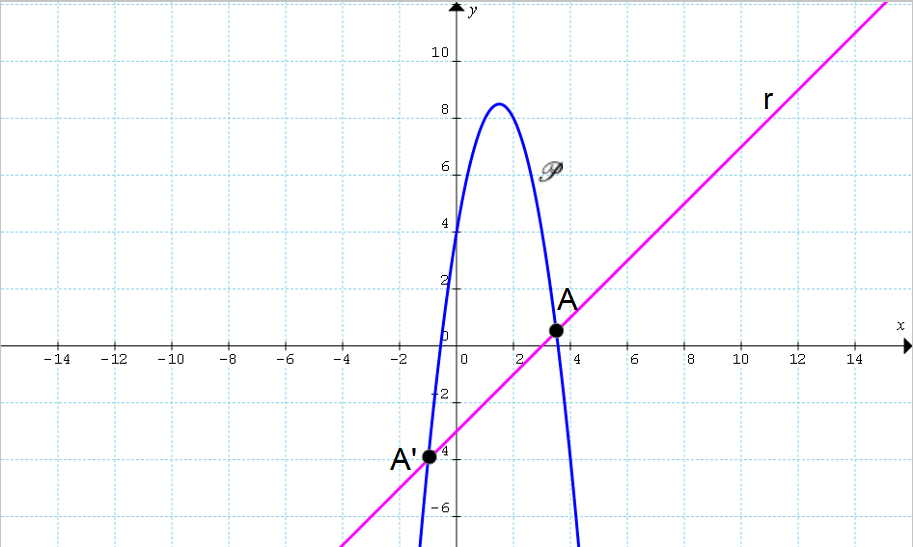
Ora, come sappiamo il teorema di Archimede richiede un rettangolo grazie al quale è possibile risalire all’area del segmento parabolico. In questo caso, per costruire tale rettangolo dobbiamo prima di tutto rappresentare nel piano cartesiano la retta {t} parallela ad {r} e tangente alla parabola.

La retta {t} cercata avrà equazione della forma generica:

t: y=mx+q

Osserviamo che tale retta, essendo parallela ad {r}, avrà ancora {m=1}. Di conseguenza per la forma generica della retta {t} possiamo scrivere:

t: y=x+q

con ordinata all’origine {q} da determinare.

Ora, la retta {t} deve essere tangente alla parabola. Impostiamo il seguente sistema:

\begin{cases}\mathscr{P}: y= -2x^2+6x+4 \\ \\ t: y=x+q \end{cases}

relativo all’intersezione tra la parabola {\mathscr{P}} e la retta {t}.

L’equazione risolvente del sistema si ottiene per confronto:

\begin{align*} &-2x^2+6x+4=x+q; \\ \\ & -2x^2+5x+4-q=0\end{align*}

Poiché la retta {t} è tangente alla parabola, il determinante dell’equazione risolvente appena scritta dovrà necessariamente essere uguale a zero:

\Delta = 0 \quad \Rightarrow \quad 25+4 \cdot 2 \cdot (4-q)=0

e quindi:

\begin{align*} &25+8\cdot(4-q)=0;\\ \\ & 25+32-8q=0;\\ \\ & 8q=25+32 \quad \Rightarrow \quad q=\dfrac{57}{8}\end{align*}

Di conseguenza, sostituendo il valore di {q} appena calcolato, abbiamo per l’equazione della retta {t}:

t: y=x+\dfrac{57}{8}

Effettivamente tracciando la retta {t} troviamo conferma che questa è parallela alla retta {r} e tangente alla parabola {\mathscr{P}}.

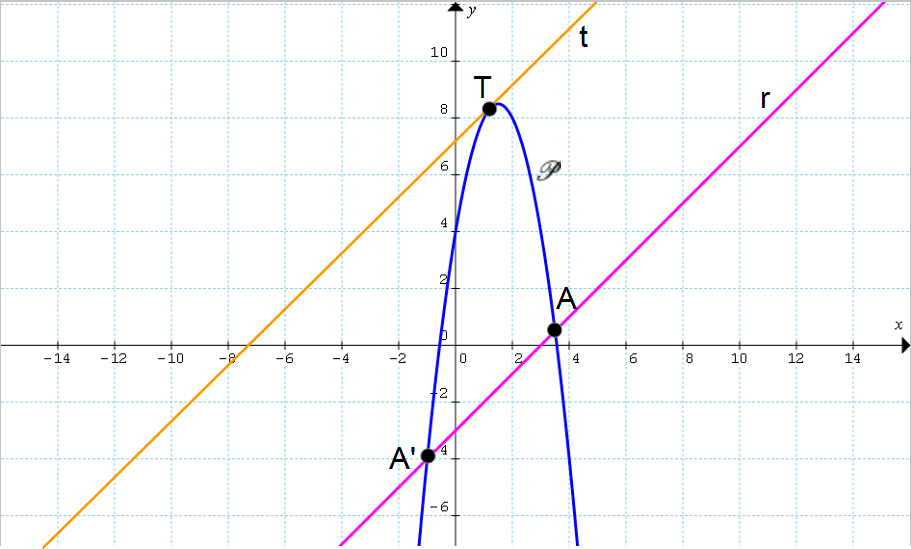
Ora, ricordando l’enunciato del teorema di Archimede nella sua forma generale, dobbiamo proiettare i punti {A'} ed {A} sulla retta {t}, perpendicolarmente alla retta {r}. Per fare ciò, l’idea è quella di scrivere le equazioni delle rette passanti rispettivamente per {A'} ed {A} e perpendicolari a {r}, e quindi intersecare ciascuna di tali rette con la retta {t}. I punti che così si ottengono saranno le proiezioni di {A'} ed {A} cercate.

Cominciamo con lo scrivere le equazioni delle rette perpendicolari a {r} e passanti per i punti {A'} ed {A}. Indichiamo tali rette rispettivamente con {r_1} ed {r_2}.

Le rette, dovendo essere perpendicolari ad {r}, avranno coefficiente angolare uguale all’opposto del reciproco del coefficiente angolare {m} relativo alla retta {r} (vedi: rette perpendicolari). Indicando quindi con {m_{r_{1,2}}} il coefficiente angolare delle rette {r_1} ed {r_2}, si ha:

m_{r_{1,2}} = -\dfrac{1}{m}=-\dfrac{1}{1}=-1

Ora, poiché le rette {r_1} ed {r_2} sono passanti rispettivamente per i punti {A'} ed {A}, aventi coordinate note, ricordando la formula della retta passante per un punto e con coefficiente angolare noto si ha:

r_1: y-y_{A'}=m_{r_{1,2}}(x-x_{A'}); \qquad  r_2: y-y_{A}=m_{r_{1,2}}(x-x_{A})

e quindi, sostituendo i valori, otteniamo rispettivamente:

\begin{align*} &r_1: y-(-4)=-1 \cdot[x-(-1)]; \\ \\ & y+4=-(x+1);\\ \\ & y=-x-1-4;\\ \\ &\boxed{ r_1: y=-x-5}\end{align*}

e:

\begin{align*} &r_2: y-\dfrac{1}{2}=-1 \left( x-\dfrac{7}{2}\right); \\ \\ & y=-x+\dfrac{7}{2}+\dfrac{1}{2}; \\ \\ & \boxed{ r_2: y=-x+4}\end{align*}

Graficamente vale la seguente rappresentazione:

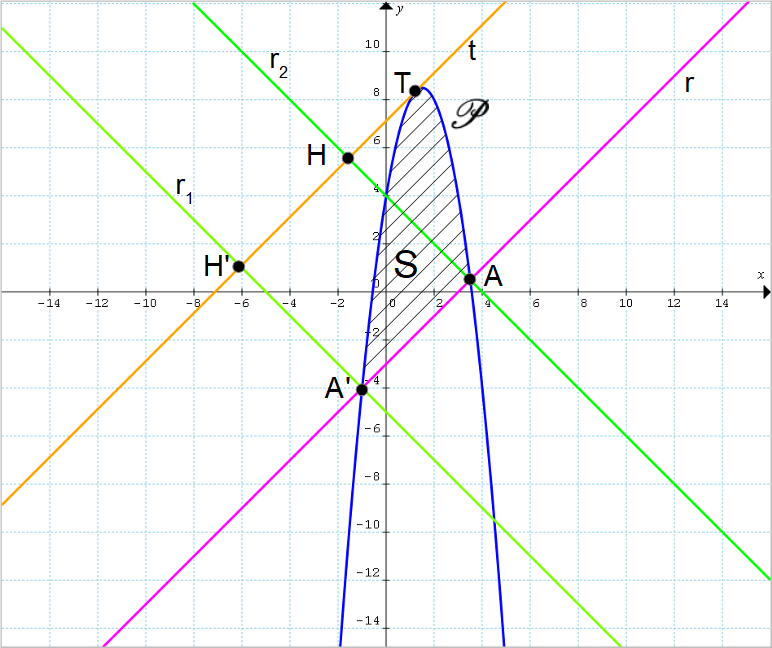
A questo punto la strada è in discesa. Basta infatti calcolare l’area del rettangolo {H'HAA'} e quindi calcolare l’area {S} del segmento parabolico evidenziato in figura grazie al teorema di Archimede.

Per il calcolo dell’area del rettangolo, dobbiamo partire dalle coordinate dei suoi vertici, e già disponiamo delle coordinate dei punti {A'} ed {A}. Le coordinate dei punti {H'} e {H} si ottengono invece dall’intersezione rispettivamente tra le rette {r_1} e {t} e le rette {r_2} e {t}. Abbiamo, per l’intersezione tra la retta {r_1} e la retta {t}:

\small \begin{cases} r_1: y=-x-5 \\ \\ t: y=x+\dfrac{57}{8}\end{cases} \quad \Rightarrow \: -x-5=x+\dfrac{57}{8} \quad \Rightarrow \: 2x=-5-\dfrac{57}{8} \quad \Rightarrow \: x=-\dfrac{97}{16}

da cui si ottengono le coordinate del punto {H'}:

H'=\left( -\dfrac{97}{16}, -\dfrac{97}{16}+\dfrac{57}{8}\right)=\left( -\dfrac{97}{16}, \dfrac{17}{16} \right)

Infine, per l’intersezione tra la retta {r_2} e {t}:

\small \begin{cases} r_2: y=-x+4 \\ \\ t: y=x+\dfrac{57}{8}\end{cases} \quad \Rightarrow \: -x+4=x+\dfrac{57}{8} \: \Rightarrow \quad 2x=4-\dfrac{57}{8} \quad \Rightarrow \: x=-\dfrac{25}{16}

da cui si ottengono le coordinate del punto {H}:

H=\left( -\dfrac{25}{16}, -\dfrac{25}{16}+\dfrac{57}{8}\right)=\left( -\dfrac{25}{16}, \dfrac{89}{16}\right)

Riportiamo infine per comodità le coordinate dei punti {A} ed {A'} calcolate in precedenza:

A=\left( \dfrac{7}{2}, \dfrac{1}{2}\right); \qquad A'=(-1,-4)

Ora disponiamo di tutto ciò che ci serve per calcolare l’area del rettangolo {H'HAA'}. Infatti, essendo note le coordinate dei suoi vertici, è immediato calcolare le misure della sua base e della sua altezza mediante la formula della distanza tra due punti nel piano. Abbiamo per l’altezza del rettangolo:

\small \begin{align*} &\overline{AH} = \sqrt{\left( x_H-x_A\right)^2+(y_H-y_A)^2}=\sqrt{\left( -\dfrac{25}{16}-\dfrac{7}{2}\right)^2+\left( \dfrac{89}{16}-\dfrac{1}{2}\right)^2}= \\ \\ & =\sqrt{\left( \dfrac{-25-56}{16}\right)^2+\left( \dfrac{89-8}{16}\right)^2}=\sqrt{\left( \dfrac{-81}{16}\right)^2+\left( \dfrac{81}{16}\right)^2}=\\ \\ & =\sqrt{\dfrac{2 \cdot 81^2}{16^2}}=\sqrt{2} \cdot \dfrac{81}{16}\end{align*}

e per la base:

\small \begin{align*} &\overline{AA'}= \sqrt{(x_{A'}-x_A)^2+(y_{A'}-y_A)^2}=\sqrt{\left( -1-\dfrac{7}{2}\right)^2+\left( -4-\dfrac{1}{2}\right)^2}=\\ \\ & =\sqrt{\left( \dfrac{-2-7}{2}\right)^2+\left( \dfrac{-8-1}{2}\right)^2}=\sqrt{\dfrac{81}{4}+\dfrac{81}{4}}=\dfrac{9}{\sqrt{2}}\end{align*}

Di conseguenza per l’area del rettangolo {H'HAA'} si ha:

\overline{AH} \cdot  \overline{AA'} = \cancel{\sqrt{2}} \cdot \dfrac{81}{16} \cdot \dfrac{9}{\cancel{\sqrt{2}}} = 81 \cdot \dfrac{9}{16}

Ed infine, applicando il teorema di Archimede, per l’area del segmento parabolico {S} abbiamo in conclusione:

S = \dfrac{2}{3} \cdot \overline{AH} \cdot \overline{AA'} = \dfrac{\cancel{2}}{\cancel{3}} \cdot 81 \cdot  \dfrac{\cancel{9}^{\scriptsize \displaystyle3}}{\cancel{16}^{\scriptsize \displaystyle8}} =81 \cdot \dfrac{3}{8}= \dfrac{243}{8}

Esempio 3

Calcolare l’area del segmento parabolico relativo alla parabola {\mathscr{P}: y = x^2+2x-6} e individuato sulla parabola stessa dalla retta {r:y = x}.

Vediamo per questo esempio il metodo più rapido basato sull’utilizzo della distanza punto-retta.

Per aiutarci a disegnare la parabola calcoliamo le coordinate del suo vertice:

V=\left( -\dfrac{b}{2a}, -\dfrac{\Delta}{4a}\right)=\left( -\dfrac{2}{2}, -\dfrac{28}{4}\right)=(-1,-7)

Inoltre, la parabola ha concavità rivolta verso l’alto e ha asse verticale.

Per la retta non abbiamo problemi in quanto si tratta della bisettrice del primo e del terzo quadrante.

Abbiamo quindi la seguente rappresentazione sul piano cartesiano:

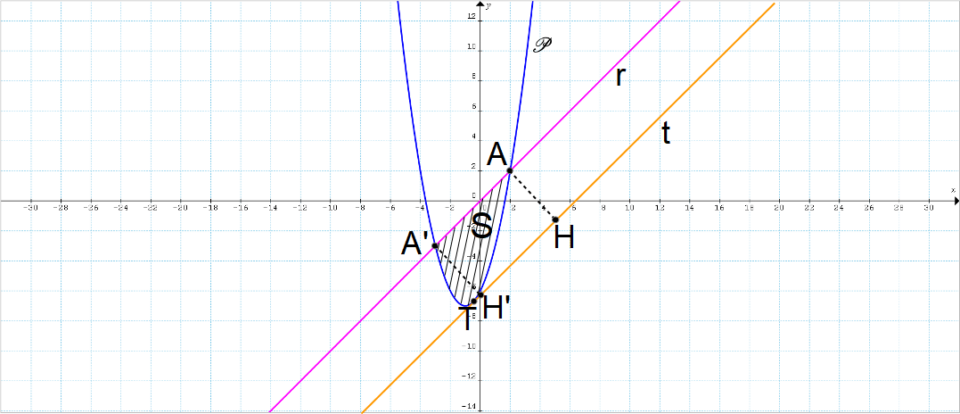
Per calcolare le coordinate dei punti {A} ed {A'} impostiamo il sistema:

\begin{cases} \mathscr{P}: y = x^2+2x-6 \\ \\ r: y = x\end{cases}

da cui otteniamo l’equazione risolvente:

\begin{align*} &x^2+2x-6=x;\\ \\ & x^2+x-6=0\end{align*}

che risolta fornisce le ascisse:

x=2 \quad \vee \quad x=-3

alle quali corrispondono le ordinate:

y=2 \quad \vee \quad y=-3

Così i punti {A} ed {A'} hanno coordinate:

A=(2,2); \qquad A'=(-3,-3)

Ora, la retta tangente {t} ha equazione in forma generale:

t: y=x+q

Il coefficiente angolare è infatti noto poiché è lo stesso della retta {r} (le due rette sono parallele).

Per determinare il valore dell’ordinata all’origine {q}, come visto nell’esempio precedente basta impostare il sistema:

\begin{cases}  \mathscr{P}: y = x^2+2x-6 \\ \\ t:y=x+q\end{cases}

scrivere la relativa equazione risolvente:

\begin{align*} &x^2+2x-6=x+q; \\ \\ & x^2 +x-6-q=0\end{align*}

e quindi imporre il determinante di tale equazione uguale a zero (la retta {t} è tangente alla parabola):

\begin{align*} &b^2-4ac=0; \\ \\ & 1- 4 \cdot 1 \cdot (-6-q)=0; \\ \\ & 1+24+4q=0;\\ \\ & q=-\dfrac{25}{4}\end{align*}

Di conseguenza l’equazione della retta {t} tangente alla parabola e parallela alla retta {r} è:

t:y=x-\dfrac{25}{4}

Adesso, piuttosto che calcolare le coordinate dei punti {H} e {H'} come fatto nell’esempio precedente, per determinare l’altezza del rettangolo {H'HAA'} possiamo utilizzare la formula della distanza punto-retta. Infatti, l’altezza del rettangolo in esame corrisponde alla distanza fra la retta {t} ed uno a scelta fra i punti {A} e {A'}, le coordinate dei quali sono note.

Scegliendo il punto {A=(2,2)} ed indicate rispettivamente con {x_A} ed {y_A} le sue coordinate abbiamo quindi:

\begin{align*} &\overline{AH}=d(A, t) = \dfrac{|y_A-(mx_A+q)|}{\sqrt{1+m^2}}= \\ \\ & =\dfrac{\left|2-\left(1 \cdot 2 -\dfrac{25}{4}\right)\right|}{\sqrt{2}}=\dfrac{\left|2- \left( \dfrac{8-25}{4}\right) \right|}{\sqrt{2}}=\dfrac{\left| 2+\dfrac{17}{4}\right|}{\sqrt{2}}=\\ \\ & =\dfrac{25}{4} \cdot \dfrac{1}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{25}{8}\sqrt{2}\end{align*}

Osserviamo la particolare forma scelta per la formula della distanza punto-retta, che in questo caso è quella relativa alla retta espressa in forma esplicita.

Abbiamo così calcolato la misura dell’altezza del rettangolo. Per la misura della base basterà semplicemente calcolare la distanza tra i due punti {A} ed {A'}:

\begin{align*} & \overline{AA'}=\sqrt{\left( x_{A'}-x_A\right)^2+\left( y_{A'}-y_A\right)^2}=\\ \\ & = \sqrt{(-3-2)^2+(-3-2)^2}=\sqrt{25+25}=\sqrt{50}=\sqrt{2 \cdot 5^2}=5\sqrt{2}\end{align*}

Così applicando il teorema di Archimede per l’area del segmento parabolico {S} otteniamo in conclusione:

S= \dfrac{2}{3} \cdot \overline{AA'} \cdot \overline{AH}  =\dfrac{\cancel{2}}{3} \cdot 5 \sqrt{2} \cdot \dfrac{25}{\cancel{8}^{\scriptsize4 \displaystyle}}\sqrt{2} = \dfrac{5}{12} \cdot 2 \cdot 25 = \dfrac{250}{12}=\dfrac{125}{6}

Grazie all’utilizzo della formula della distanza punto-retta siamo riusciti a determinare la misura dell’area del segmento parabolico {S} senza dover calcolare le coordinate di tutti i vertici del rettangolo {H'HAA'}. Di conseguenza, non è stato necessario scrivere le equazioni delle rette perpendicolari a {r} e passanti per i punti {A} e {A'} e quindi determinare i relativi punti di intersezione con la retta {t}, diversamente da quanto fatto nell’esempio precedente.

Per quanto riguarda il teorema di Archimede ed in particolare il calcolo dell’area di un segmento parabolico è tutto. Con questa lezione termina anche il corso di lezioni dedicato alla parabola. Per chi desidera approfondire, è in verità disponibile un’ultima lezione, dedicata alla parabola con asse obliquo. L’argomento, tuttavia, non è in genere trattato nelle scuole superiori.

Un saluto a tutti voi e buon proseguimento con SìMatematica!