Tangente ad una parabola in un punto

 - 

Parabola (scuole superiori)

Per determinare l’equazione della retta tangente ad una parabola in un suo punto è possibile porre uguale a zero il determinante dell’equazione risolvente del sistema dato dalle equazioni della parabola e della generica retta passante per il punto di tangenza, oppure è possibile utilizzare in alternativa le formule di sdoppiamento.

In questa lezione vedremo quindi come determinare l’equazione della tangente ad una parabola in un punto appartenente alla parabola stessa utilizzando due differenti metodi. Per comprendere invece come condurre le rette tangenti ad una parabola passanti per un punto esterno alla parabola stessa ci sarà di aiuto la lezione successiva.

Il metodo basato sull’annullamento del determinante dell’equazione risolvente è del tutto simile al metodo visto per la circonferenza (vedi la parte finale della lezione sulla tangente ad una circonferenza in un punto). Osserviamo invece che, diversamente dal caso della circonferenza, nella parabola non è possibile determinare l’equazione della retta tangente ad un punto della parabola stessa utilizzando delle relazioni di perpendicolarità. Tuttavia, è comunque possibile ricorrere alle formule di sdoppiamento, secondo un approccio del tutto simile a quello utilizzato a suo tempo per la circonferenza.

La tecnica che si basa sull’annullamento del determinante dell’equazione risolvente richiede dei calcoli a volte un po’ pesanti (ma non come nel caso della circonferenza), tuttavia la procedura da seguire è abbastanza meccanica. Più fluida e con calcoli molto più agili è invece il metodo basato sulle formule di sdoppiamento ma, come visto nel caso della parabola, si ha l’inconveniente di dover ricordare tali formule. Per cui ciascun metodo per determinare l’equazione della retta tangente ad una parabola in un punto ad essa appartenente presenta i suoi vantaggi e svantaggi.

Retta tangente ad una parabola in un punto imponendo il determinante dell’equazione risolvente uguale a zero

Dalla precedente lezione sulle intersezioni di una parabola con una retta, sappiamo che per determinare gli eventuali punti di intersezione tra una retta e una parabola è possibile impostare un sistema contenente le rispettive equazioni. Ad esempio, nel caso di una parabola con asse verticale {\mathscr{P}: y=ax^2+bx+c} e una retta {t:ax+by+c=0} il sistema che dovremo scrivere è il seguente:

\begin{cases}\mathscr{P}: y=ax^2+bx+c \\ \\ t:ax+by+c=0 \end{cases}

Ora, nel nostro caso è nota soltanto l’equazione della parabola ma non è nota l’equazione della retta. Sappiamo comunque che la retta {t} è tangente alla parabola nel punto {T=(x_T, y_T)} di coordinate note.

E’ quindi possibile esprimere l’equazione della retta tangente alla parabola data nella seguente forma:

t:y-y_T=m(x-x_T)

Infatti la retta tangente passa per il punto {T}, e quindi la sua equazione avrà la stessa forma dell’equazione della generica retta passante per {T}. Qui in particolare abbiamo utilizzato la formula della retta passante per un punto e con pendenza nota, anche se nel caso in esame, in realtà, la pendenza della retta non è nota. Di conseguenza, possiamo soltanto limitarci, per ora, a lasciare indicato il coefficiente angolare con la quantità {m}. Tuttavia, il nostro obiettivo sarà proprio ricavare il valore del coefficiente angolare {m}, corrispondente alla retta tangente cercata. E noto il valore di {m}, sarà possibile scrivere l’equazione della retta tangente alla parabola data nel punto {T}.

Tenendo conto della particolare forma scritta per la retta tangente {t} il precedente sistema diviene:

\begin{cases}\mathscr{P}: y=ax^2+bx+c \\ \\ t:y-y_T=m(x-x_T) \end{cases}

Per precisione, osserviamo che l’equazione per {t} che compare nel sistema rappresenta al variare di {m} nei reali un fascio di rette. Così, il nostro obiettivo formalmente è quello di determinare il valore di {m} che corrisponde alla retta del fascio tale da essere tangente alla parabola nel punto {T}. E il punto {T} rappresenta il centro del fascio. Tuttavia, per semplificare il linguaggio troviamo più comodo parlare di “generica retta passante per il punto {T}“.

Ora, riscriviamo il sistema esplicitando la variabile {y} nell’equazione della generica retta {t}:

\begin{cases}\mathscr{P}: y=ax^2+bx+c \\ \\ t:y=m(x-x_T)+y_T \end{cases}

Calcoliamo inoltre il prodotto al secondo membro della seconda equazione a sistema:

\begin{cases}\mathscr{P}: y=ax^2+bx+c \\ \\ t:y=mx-mx_T+y_T \end{cases}

A questo punto è possibile impostare la risoluzione del sistema per confronto, ottenendo un’equazione di secondo grado in {x} che rappresenta l’equazione risolvente del sistema. Considerando separatamente tale equazione abbiamo nel nostro caso:

ax^2+bx+c=mx-mx_T+y_T

ovvero raccogliendo opportunamente i termini:

ax^2+(b-m)x+c+mx_T-y_T=0

Abbiamo quindi un’equazione di secondo grado nella variabile {x}.

Per meglio vedere che la precedente equazione è un’equazione di secondo grado in forma normale, basta porre {A=a, B=b-m} ed infine {C=c+mx_T-y_T}. In tal modo l’equazione risolvente è esprimibile come:

Ax^2+Bx+C=0

Ora, il nostro obiettivo non è risolvere l’equazione rispetto a {x}. E del resto, ciò non sarebbe nemmeno possibile poiché il valore del coefficiente angolare {m} non è noto.

Tuttavia, poiché la retta {t} è tangente alla parabola, sappiamo per certo che il determinante dell’equazione risolvente il sistema dovrà necessariamente essere nullo. Così, possiamo scrivere:

\Delta = 0

ovvero:

B^2-4AC=0

e quindi, tenendo conto delle espressioni corrispondenti alle lettere {A,B} e {C}:

(b-m)^2-4\cdot a \cdot (c+mx_T-y_T)=0

Calcolando i prodotti al primo membro ed eseguendo opportuni raccoglimenti:

\begin{align*}&b^2-2bm+m^2-4ac-4ax_Tm+4ay_T=0; \\ \\ & m^2-2bm-4ax_Tm+b^2-4ac+4ay_T=0;\\ \\ & \underbrace{\boxed{m^2+(-2b-4ax_T)m+b^2-4ac+4ay_T=0}}_{\text{caso di una parabola con asse verticale - non serve impararla a memoria}}\end{align*}

Otteniamo così un’equazione di secondo grado nella variabile {m} che, risolta, consente di ricavare il valore del coefficiente angolare corrispondente alla retta tangente ad una parabola con asse verticale nel punto {T}. Ed infine, è possibile determinare l’equazione di tale retta tangente sostituendo il valore di {m} nell’equazione della generica retta passante per {T}.

Osserviamo che non è assolutamente necessario imparare a memoria la forma generale dell’equazione risolvente del sistema (l’equazione evidenziata nel riquadro, valida tra l’altro solo per parabole con asse verticale). Questa può essere piuttosto ricavata caso per caso utilizzando la procedura appena adottata (esempio 1 a seguire).

Precisiamo infine che utilizzando la stessa procedura è possibile ricavare, sia in generale, sia caso per caso, l’equazione risolvente del sistema anche nel caso in cui la parabola abbia asse di simmetria orizzontale. Per brevità omettiamo la forma generale dell’equazione risolvente relativa al caso di una parabola con asse orizzontale. Mostreremo invece come ricavare tale equazione caso per caso, che è ciò che unicamente serve per gli esercizi (esempi 2 e 3 a seguire).

Ma vediamo subito un esempio su come determinare l’equazione della retta tangente ad una parabola passante per un punto appartenente alla parabola stessa (parabola con asse verticale). Successivamente, faremo un’importantissima precisazione relativa al caso di una parabola con asse di simmetria orizzontale.

Esempio 1

Determinare l’equazione della retta {t} tangente alla parabola {\mathscr{P}: y=5x^2+3x-6} nel suo punto {T=(1,2)}.

Le coordinate del punto {T} di tangenza sono {x_T=1} e {y_T=2}. Di conseguenza, la retta tangente che stiamo cercando è esprimibile come la generica retta passante per il punto {T} come:

t:y-y_T=m(x-x_T)

ovvero:

t:y-2=m(x-1)

e quindi:

t:y=mx-m+2

Mettiamo a sistema l’equazione della parabola e l’equazione per la generica retta {t} appena scritta:

\begin{cases} \mathscr{P}: y=5x^2+3x-6 \\ \\ t:y=mx-m+2 \end{cases}

Impostiamo la risoluzione del sistema per confronto, in modo da poter scrivere l’equazione risolvente (ricordiamo che non dobbiamo determinare le soluzioni del sistema):

\begin{cases} mx-m+2=5x^2+3x-6 \\ \\ y=mx-m+2\end{cases}

Concentriamoci sulla prima equazione a sistema, che è l’equazione risolvente del sistema stesso:

\begin{align*} &mx-m+2=5x^2+3x-6; \\ \\ & 5x^2+3x-mx-6+m-2=0;\\ \\ & \underbrace{5}_{A}x^2+\underbrace{(3-m)}_{B}x+\underbrace{m-8}_{C}=0\end{align*}

L’equazione è della forma {Ax^2+Bx+c} con {A=5, B=3-m} e {C=m-8}. Per ricavare il valore di {m} corrispondente alla retta tangente alla parabola nel punto {T}, imponiamo il determinante dell’equazione risolvente uguale a zero:

\begin{align*} &B^2-4AC=0; \\ \\ & (3-m)^2-4 \cdot 5 \cdot (m-8)=0;\\ \\ &9-6m+m^2-20m+160=0;\\ \\ & m^2-26m+169=0 \end{align*}

Ora non resta che risolvere l’equazione appena scritta rispetto a {m}. Osserviamo che si tratta di un’equazione di secondo grado in forma normale. Utilizzando l’opportuna formula risolutiva (ad esempio quella ridottissima) abbiamo:

\begin{align*} &m_{1,2}=13 \pm \sqrt{(-13)^2-169}\end{align*}=13 \pm 0=13

Di conseguenza abbiamo ottenuto due soluzioni reali e coincidenti per l’equazione e quindi a lato pratico un unico valore per il coefficiente angolare {m}. Sostituendo tale valore nell’equazione della generica retta passante per {T} abbiamo infine:

\begin{align*} &t:y=mx-m+2 \quad \text{con} \quad m=13 \\ \\ & y=13x-13+2; \\ \\ & \boxed{t:y=13x-11}\end{align*}

e questa è l’equazione della retta tangente alla parabola data nel punto {T=(1,2)}.

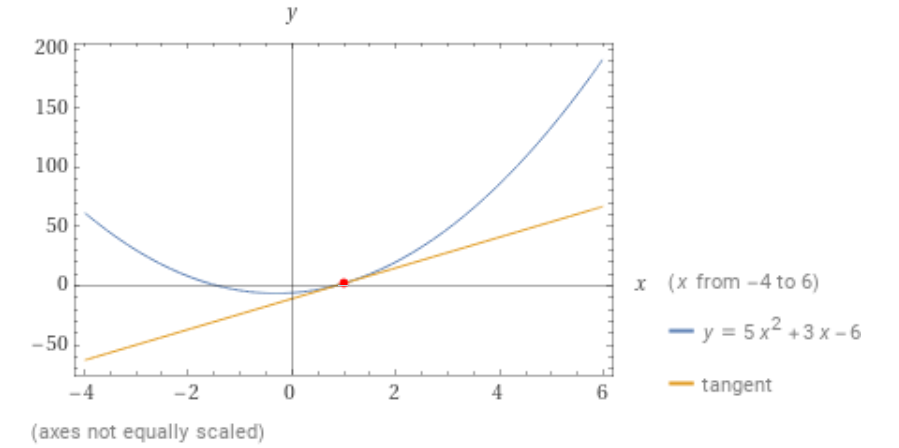
Osserviamo che nella figura gli assi non seguono la stessa scala volutamente. In tal modo è infatti possibile apprezzare meglio il fatto che la retta {t} è tangente alla parabola. Effettivamente utilizzando la stessa scala in entrambi gli assi, la retta tende a confondersi con un ramo della parabola.

Caso di una parabola con asse di simmetria orizzontale

Nel caso di una parabola con asse di simmetria verticale, il metodo proposto consente sempre di determinare l’equazione della retta tangente in un dato punto appartenente alla parabola. Infatti, le uniche possibili rette tangenti alla parabola sono le rette non parallele agli assi coordinati e la retta orizzontale passante per il vertice della parabola. E le equazioni di tali rette sono sempre esprimibili come:

y-y_T=m(x-x_T)

ove {x_T} ed {y_T} sono le coordinate del punto di tangenza {T}. In altre parole, esiste sempre un valore del coefficiente angolare {m} tale da corrispondere ad una qualsiasi retta tangente alla parabola in un punto appartenente ad essa.

Ora, l’equazione della generica retta passante per il punto {T} appena scritta non è in grado di rappresentare una retta verticale. Infatti, per le rette verticali il coefficiente angolare {m} non è definito.

Ciò per le parabole con asse di simmetria verticale non è un problema. Infatti, come sappiamo dalla precedente lezione, nel caso di una parabola con asse verticale una retta verticale sarà sempre e soltanto secante alla parabola. Per cui, il metodo basato sull’annullamento del determinante dell’equazione risolvente consente sempre di ricavare il valore di {m} corrispondente alla retta tangente cercata.

Diverso è invece il caso di una parabola con asse di simmetria orizzontale. In questo caso, infatti, non è possibile ottenere il valore del coefficiente angolare corrispondente alla retta tangente alla parabola nel vertice. Tale retta è, infatti, verticale. E per una retta verticale il coefficiente angolare {m} non è definito.

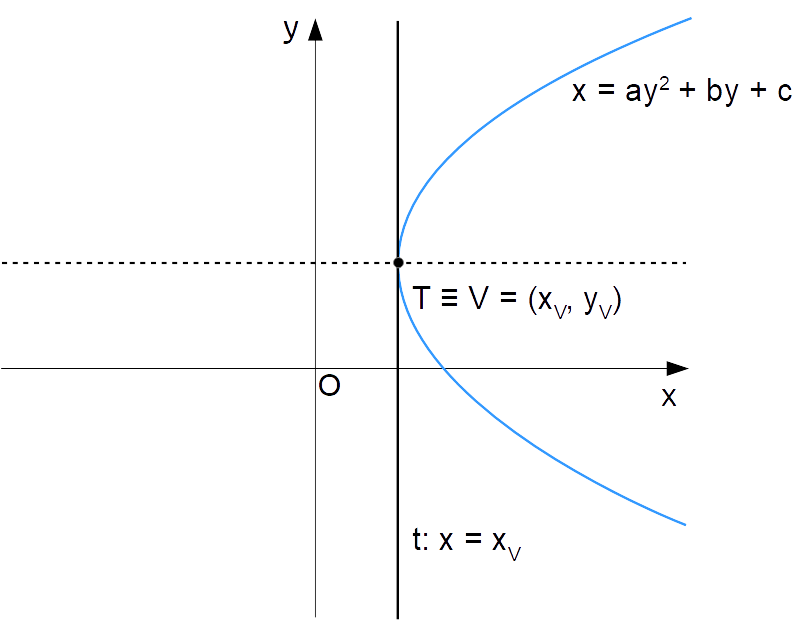
Se dunque nel ricercare il coefficiente angolare della retta tangente ad un dato punto appartenente alla parabola non troviamo alcun valore di {m} (parabola con asse orizzontale), ciò significa che il punto stesso è il vertice della parabola. Ma in tal caso, l’equazione della retta tangente sarà semplicemente:

t: x = x_V

ove {x_V} è l’ascissa del vertice della parabola. Infatti, in tale circostanza la retta tangente è data dalla retta verticale passante per il vertice della parabola stessa.

Infine, nel caso di rette tangenti non parallele agli assi coordinati, è sempre possibile determinare il corrispondente valore di {m}, anche nel caso di una parabola con asse di simmetria orizzontale.

Esempio 2

Scrivere l’equazione della retta tangente alla parabola di equazione {\mathscr{P}: x = y^2+2y+6} nel punto {T=(5,-1)} appartenente alla parabola stessa.

Proviamo a risolvere il problema ricercando il coefficiente angolare {m}. Impostiamo il sistema, come nell’esempio visto in precedenza:

\begin{cases}\mathscr{P}: x = y^2+2y+6 \\ \\ t:y+1=m(x-5) \end{cases}

Riesprimiamo la seconda equazione a sistema in modo da esplicitare la variabile {x}. In tal modo sarà possibile determinare l’equazione risolvente del sistema per confronto.

\small \begin{cases}x = y^2+2y+6 \\ \\y=mx-5m-1 \quad \rightarrow \: mx=y+5m+1 \: \rightarrow \: x=\dfrac{1}{m}y+5+\dfrac{1}{m}, \quad m\neq 0\end{cases}

Osserviamo che la condizione {m \neq 0} non è un problema. Infatti, al valore {m=0} corrisponde una retta orizzontale, che è sempre secante ad una parabola con asse orizzontale. Escludendo il valore {m=0} non escludiamo dunque una possibile retta tangente.

Otteniamo quindi per confronto l’equazione risolvente:

\begin{align*} &\dfrac{1}{m}y+5+\dfrac{1}{m}=y^2+2y+6; \\ \\ &y^2+\left( 2-\dfrac{1}{m}\right)y+6-5-\dfrac{1}{m}=0;\\ \\ & y^2+\left( 2-\dfrac{1}{m}\right)y+1-\dfrac{1}{m}=0\end{align*}

Abbiamo un’equazione di secondo grado della forma {Ay^2+By+C=0} con {A=1, B = 2-\dfrac{1}{m}} e {C=1-\dfrac{1}{m}}.

Imponendo il determinante uguale a zero abbiamo:

\begin{align*} &\left( 2-\dfrac{1}{m}\right)^2-4 \cdot 1 \cdot \left( 1-\dfrac{1}{m}\right)=0; \\ \\ & \cancel{4}-\cancel{\dfrac{4}{m}}+\dfrac{1}{m^2}-\cancel{4}+\cancel{\dfrac{4}{m}}=0;\\ \\ & \dfrac{1}{m^2}=0 \quad \Rightarrow \quad \text{impossibile}\end{align*}

L’equazione è impossibile e dunque non otteniamo alcun valore per {m}. Ma ciò significa che non esiste alcuna retta tangente alla parabola nel punto dato? La risposta è no.

Infatti, se proviamo a calcolare le coordinate del vertice della parabola, otteniamo (attenzione a prendere i coefficienti dall’equazione della parabola):

x_V=-\dfrac{\Delta}{4a}=-\dfrac{b^2-4ac}{4a}=-\dfrac{2^2-4 \cdot 1 \cdot 6}{4 \cdot 1}=5

e:

y_V=-\dfrac{b}{2a}=-\dfrac{2}{2\cdot1}=-1

Così il vertice della parabola è {V=(5,-1)}, ed effettivamente coincide con il punto di tangenza del testo del problema.

Di conseguenza, la retta tangente cercata esiste ed è la retta verticale passante per il vertice, ovvero:

t:x=5

Vediamo ora un esempio relativo sempre ad una parabola con asse di simmetria orizzontale ma con retta tangente non verticale.

Esempio 3

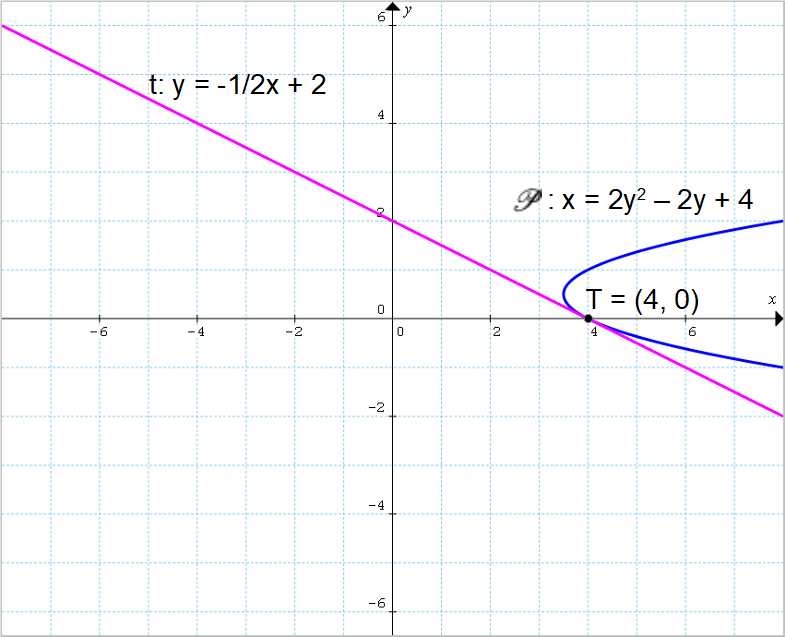
Scrivere l’equazione della retta {t} tangente alla parabola {\mathscr{P}:x=2y^2-2y+4} nel punto {T=(4,0)} appartenente alla parabola stessa.

Osserviamo che il punto {T} non corrisponde sicuramente al vertice della parabola. Infatti, l’ordinata del punto {T} è zero ma l’ordinata del vertice è diversa da zero. Infatti, il coefficiente {b} nell’equazione della parabola è non nullo (ricordiamo che l’ordinata del vertice di una parabola con asse orizzontale è data da {-\dfrac{b}{2a}}).

Possiamo quindi ricercare il valore del coefficiente angolare {m} corrispondente alla retta tangente alla parabola nel punto {T}, certi che riusciremo a trovare tale valore.

Date le coordinate del punto {T}, la generica retta passante per il punto stesso ha equazione:

y-0=m(x-4) \quad \Rightarrow \quad t:y=mx-4m

Esplicitiamo la variabile {x} dall’equazione della retta, ponendo la condizione {m \neq 0}. Ricordiamo ancora che tale condizione non rappresenta un problema, in quanto un valore nullo del coefficiente angolare corrisponde ad una retta orizzontale, in questo caso parallela all’asse della parabola e quindi secante la parabola stessa.

mx=y+4m \quad \Rightarrow \quad t:x=\dfrac{1}{m}y+4

Impostiamo il sistema:

\begin{cases}\mathscr{P}:x=2y^2-2y+4 \\ \\   t:x=\dfrac{1}{m}y+4\end{cases}

Scriviamo l’equazione risolvente del sistema per confronto:

2y^2-2y+\cancel{4}=\dfrac{1}{m}y+\cancel{4}

otteniamo:

2y^2+\left( -2-\dfrac{1}{m}\right)y=0

Ci ritroviamo con un’equazione di secondo grado spuria. Manca infatti il termine noto. Tuttavia, dobbiamo comunque scrivere il determinante corrispondente a tale equazione. Infatti, per imporre la condizione di tangenza della retta alla parabola dobbiamo imporre che tale determinante sia nullo. Ma ciò non rappresenta un problema. In effetti, ponendo {A=2, B=-2-\dfrac{1}{m}} e {C=0} l’equazione diviene della forma:

Ay^2+By+C=0

ed è quindi possibile scriverne il determinante.

Ponendo in particolare il determinante uguale a zero abbiamo:

\begin{align*} &B^2-4AC=0;\\ \\ & \left( -2-\dfrac{1}{m}\right)^2-4 \cdot 2 \cdot 0=0;\\ \\ & \left( -2-\dfrac{1}{m}\right)^2=0;\\ \\ & 4+\dfrac{1}{m^2}+\dfrac{4}{m}=0;\\ \\ & \dfrac{4m^2+1+4m}{m^2}=0; \\ \\ & 4m^2+4m+1=0, \qquad m \neq 0\end{align*}

Risolvendo l’equazione appena ottenuta nella variabile {m} abbiamo:

\begin{align*} &m_{1,2}=\dfrac{-2\pm \sqrt{2^2-4\cdot1}}{4}=-\dfrac{2}{4}=-\dfrac{1}{2}\end{align*}

Otteniamo così per la retta tangente cercata il coefficiente angolare {m=-\dfrac{1}{2}}. L’equazione ha infatti due soluzioni reali e coincidenti e quindi in pratica fornisce un solo valore per il coefficiente angolare.

Di conseguenza sostituendo il valore {m=-\dfrac{1}{2}} nell’equazione:

t:x=\dfrac{1}{m}y+4

otteniamo:

t:x=-2y+4

ovvero in forma esplicita:

-2y=x-4 \quad \Rightarrow \quad t: y=-\dfrac{1}{2}x+2

e questa è l’espressione dell’equazione relativa alla retta tangente alla parabola {\mathscr{P}} nel punto {T=(4,0)}.

Come determinare l’equazione della retta tangente ad una parabola in un suo punto con le formule di sdoppiamento

In modo del tutto simile a quanto visto a suo tempo per la circonferenza, è possibile determinare l’equazione della retta tangente ad una parabola in un punto appartenente alla parabola stessa mediante le formule di sdoppiamento.

Le formule di sdoppiamento consentono di determinare l’equazione della retta tangente ad una parabola in un suo punto in tutti i casi, anche nella circostanza ove la parabola abbia asse orizzontale e la retta tangente sia verticale. Tuttavia, lo svantaggio che si ha nell’utilizzare le formule di sdoppiamento è dato dalla necessità di dover ricordare le formule stesse.

A partire dall’equazione della parabola, indifferentemente con asse orizzontale o verticale, è possibile scrivere l’equazione della retta tangente alla parabola in un dato punto {T=(x_T, y_T)} appartenente alla parabola stessa operando le trasformazioni:

x^2 \rightarrow  x_T \cdot x, \qquad y^2\rightarrow y_T \cdot y, \qquad x\rightarrow \dfrac{x+x_T}{2}, \qquad y \rightarrow \dfrac{y+y_T}{2}

Al fine di evitare confusione, precisiamo che se la parabola ha asse verticale, questa ha equazione:

y=ax^2+bx+c

e quindi la formula di sdoppiamento relativa al termine in {y^2} non serve.

In modo del tutto simile, se la parabola ha asse orizzontale, ovvero ha equazione:

x=ay^2+by+c

la formula di sdoppiamento relativa al termine in {x^2} non serve.

E’ altresì importante osservare che le formule di sdoppiamento appena scritte sono le stesse utilizzate a suo tempo per la circonferenza. Così, se già avete familiarità con le formule di sdoppiamento relative alla circonferenza, la strada è già spianata per la parabola.

Riprendiamo a questo punto i tre precedenti esempi, utilizzando stavolta le formule di sdoppiamento.

Esempio 1 bis

Determinare l’equazione della retta {t} tangente alla parabola {\mathscr{P}: y=5x^2+3x-6} nel suo punto {T=(1,2)}. Utilizzare le formule di sdoppiamento.

Poiché il punto di tangenza è {T=(1,2)} abbiamo:

x_T=1, \quad y_T=2

Poiché l’equazione della parabola è:

y=5x^2+3x-6

abbiamo bisogno delle formule di sdoppiamento relative alle quantità {y}, {x^2} e {x}. Si ha:

y \rightarrow \dfrac{y+y_T}{2}

ovvero, sostituendo il valore dell’ordinata del punto {T}:

\boxed{y \rightarrow \dfrac{y+2}{2}}

Per la quantità {x^2} abbiamo:

x^2 \rightarrow x_T \cdot x

ovvero:

{x^2 \rightarrow 1 \cdot x}

e quindi:

\boxed{x^2 \rightarrow x}

Infine, per la quantità {x}:

x \rightarrow \dfrac{x+x_T}{2}

e quindi:

\boxed{x \rightarrow \dfrac{x+1}{2}}

Ora, si tratta di effettuare nell’equazione della parabola le sostituzioni evidenziate nei riquadri. In particolare, presa l’equazione della parabola data nel testo, dovremo sostituire alla {y} la quantità {\dfrac{y+2}{2}}, alla {x^2} la quantità {x}, e infine alla {x} la quantità {\dfrac{x+1}{2}}. Procedendo in questo modo dall’equazione della parabola otteniamo:

\begin{align*} &\overbrace{y}^{\small\frac{y+2}{2}}=5\overbrace{x^2}^{x}+3\overbrace{x}^{\small \frac{x+1}{2}}-6; \\ \\ & \dfrac{y+2}{2}=5 x + 3 \cdot \dfrac{x+1}{2}-6=0;\\ \\ & \dfrac{y+2}{2}-5x-\dfrac{3}{2}x-\dfrac{3}{2}+6=0;\\ \\ & \dfrac{y+2-10x-3x-3+12}{\cancel{2}}=0;\\ \\ & y-13x+11=0;\\ \\ & t: y=13x-11\end{align*}

Ritroviamo così l’equazione della retta tangente alla parabola nel punto {t} già determinata nell’esempio 1 precedente.

Esempio 2 bis

Scrivere l’equazione della retta tangente alla parabola di equazione {\mathscr{P}: x = y^2+2y+6} nel punto {T=(5,-1)} appartenente alla parabola stessa. Utilizzare le formule di sdoppiamento.

Essendo {T=(5,-1)} si ha:

x_T=5, \qquad y_T=-1

Le formule di sdoppiamento da utilizzare sono di conseguenza:

x \rightarrow \dfrac{x+5}{2}; \qquad y^2\rightarrow -y; \qquad y \rightarrow \dfrac{y-1}{2}

Così dall’equazione della parabola otteniamo:

\begin{align*} &\dfrac{x+5}{2}=-y+\cancel{2}\cdot\dfrac{y-1}{\cancel{2}}+6;\\ \\ & \dfrac{x+5}{2}=-\cancel{y}+\cancel{y}-1+6;\\ \\ & \dfrac{x+5}{2}=5;\\ \\ & \dfrac{x+5-10 }{\cancel{2}}=0; \\ \\ &x-5=0 \quad \Rightarrow \quad t:x=5 \end{align*}

Effettivamente ritroviamo l’equazione già determinata nel precedente esempio 2. Osserviamo che le formule di sdoppiamento consentono di ottenere direttamente l’equazione della retta tangente cercata anche se questa è verticale (le retta {t} del caso in esame è verticale).

Esempio 3 bis

Scrivere l’equazione della retta {t} tangente alla parabola {\mathscr{P}:x=2y^2-2y+4} nel punto {T=(4,0)} appartenente alla parabola stessa. Utilizzare le formule di sdoppiamento.

Procedendo come negli esempi precedenti, abbiamo le trasformazioni:

x \rightarrow \dfrac{x+4}{2}, \qquad y^2 \rightarrow 0, \qquad y \rightarrow \dfrac{y}{2}

Di conseguenza a partire dall’equazione della parabola in esame otteniamo:

\begin{align*} & \dfrac{x+4}{2}=2 \cdot 0-2 \cdot \dfrac{y}{2}+4;\\ \\ &\dfrac{x+4}{2}=-y+4;\\ \\ & \dfrac{x+4+2y-8}{\cancel{2}}=0;  \\ \\ & x+2y-4=0 ; \\ \\ &t: y=-\dfrac{1}{2}x+2\end{align*}

Ritroviamo in conclusione anche per quest’ultimo esempio lo stesso risultato ottenuto con il metodo del determinante nullo dell’equazione risolvente.

Conclusioni

Abbiamo così visto come determinare l’equazione della tangente ad una parabola in un punto appartenente alla parabola stessa, utilizzando due differenti metodi. Se non si hanno problemi a ricordare le formule di sdoppiamento, queste permettono di determinare la retta tangente cercata con calcoli piuttosto leggeri. Ed inoltre l’utilizzo delle formule di sdoppiamento è piuttosto meccanico e non richiede particolari accorgimenti ad esempio nel caso in cui la retta tangente cercata risulti verticale (retta tangente al vertice di una parabola con asse orizzontale).

Il metodo basato sulla ricerca del coefficiente angolare annullando il determinante dell’equazione risolvente richiede invece dei calcoli più scomodi, anche se comunque non particolarmente pesanti. E come abbiamo visto, il caso relativo alla retta tangente per il vertice ad una parabola con asse orizzontale richiede un ragionamento a parte, anche se non complicato.

Lasciamo a voi la scelta del metodo che più si adatta alle vostre esigenze, ricordando sempre di osservare le indicazioni fornite dal vostro insegnante.

Per questa lezione è tutto. Nella prossima lezione vedremo come condurre le rette tangenti ad una data parabola passanti per un fissato punto esterno alla parabola stessa. Inoltre, nella lezione ancora successiva ci occuperemo delle condizioni necessarie e sufficienti per individuare univocamente una parabola nel piano cartesiano. Un saluto a tutti voi e buon lavoro!