Parabola con vertice nell’origine e passante per l’origine

 - 

Parabola (scuole superiori)

Una parabola con asse verticale e vertice nell’origine ha equazione y = ax², mentre una parabola con asse verticale e passante per l’origine ha equazione y = ax² + bx. In modo del tutto simile, una parabola con asse orizzontale e vertice nell’origine ha equazione x = ay², mentre una parabola con asse orizzontale e passante per l’origine ha equazione x = ay² + by.

Dopo aver visto l’equazione della parabola, in questa lezione vedremo quale forma presenta l’equazione stessa nel caso in cui la parabola abbia vertice nell’origine o comunque passi per l’origine degli assi. Vedremo in particolare cosa succede in entrambe le casistiche di parabola con asse di simmetria verticale ed orizzontale.

Ci occuperemo infine anche del caso nel quale il vertice della parabola non coincida necessariamente con l’origine ma comunque appartenga ad uno dei due assi coordinati.

Parabola con vertice nell’origine

Vediamo come si riduce l’equazione di una parabola con asse verticale nel caso in cui questa abbia vertice {\boldsymbol{V}} nell’origine degli assi. In altre parole, ci chiediamo quale forma assume l’equazione di una parabola con asse verticale qualora sia {V=(0,0)}.

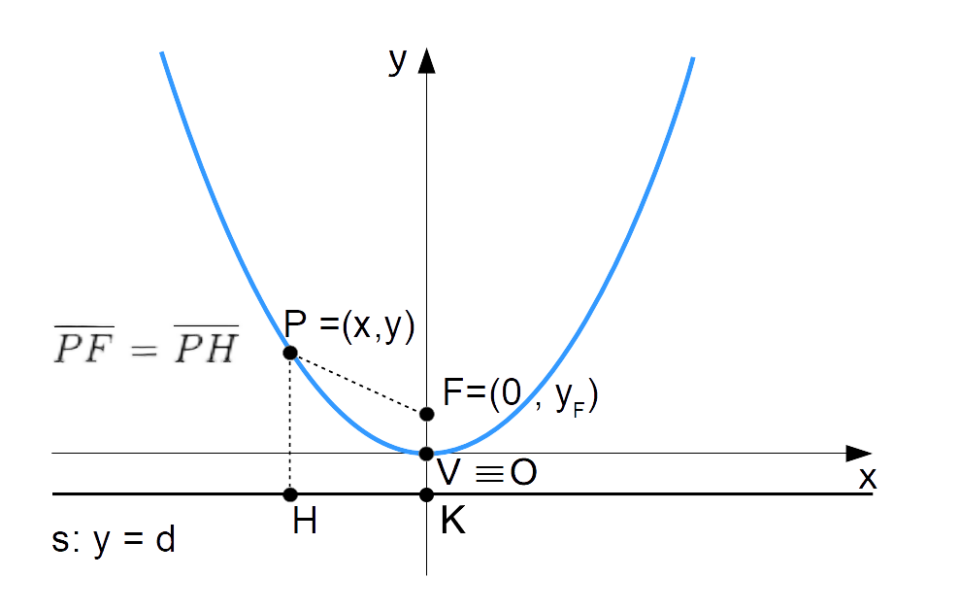
Ricordiamo che in una parabola con asse verticale il fuoco e il vertice hanno la stessa ascissa. Di conseguenza, poiché il vertice della parabola coincide in questo caso con l’origine, l’ascissa del fuoco sarà uguale a zero.

Inoltre, sempre in forza del fatto che il vertice giace nell’origine, si ha anche {d=-y_F}. E’ immediato convincersi di questo osservando che per la definizione di parabola come luogo geometrico deve necessariamente essere {\overline{FV}= \overline{VK}}. Di conseguenza, l’ascissa del punto {K} dovrà essere uguale a {-y_F}, e tale quantità coincide con la distanza con segno {d} della direttrice dall’origine.

Ora, ricordando la definizione di parabola come luogo geometrico, imponendo l’uguaglianza:

\overline{PF}=\overline{PH}

abbiamo in questo caso (formula della distanza tra due punti nel piano):

\sqrt{(x_F-x)^2+(y_F-y)^2}=|d-y|

ovvero, tenendo conto che {x_F=0} e che {d=-y_F}:

\sqrt{x^2+(y_F-y)^2}=|-y_F-y|

Eleviamo entrambi i membri al quadrato (ciò è possibile senza alcuna discussione poiché entrambi i membri sono quantità sempre positive):

x^2+(y_F-y)^2=(-y_F-y)^2

Sviluppiamo i quadrati:

x^2+\cancel{y_F^2}-2y_Fy+\cancel{y^2}=\cancel{y_F^2}+2y_Fy+\cancel{y^2}

Ora, il nostro obiettivo è ottenere un’uguaglianza del tipo {y=f(x)}, poiché questa è la forma dell’equazione di una parabola con asse di simmetria verticale. Abbiamo:

\begin{align*} &2y_Fy+2y_Fy=x^2; \\ \\ & (2y_F+2y_F)y=x^2;\\ \\ & 4y_Fy=x^2;\\ \\ & y=\dfrac{1}{4y_F}x^2\end{align*}

Infine, ponendo {a=\dfrac{1}{4y_F}} abbiamo in conclusione l’equazione:

\boxed{y=ax^2}, \qquad a \neq 0, \quad a \in \R

che rappresenta l’equazione di una parabola con asse verticale e con vertice nell’origine.

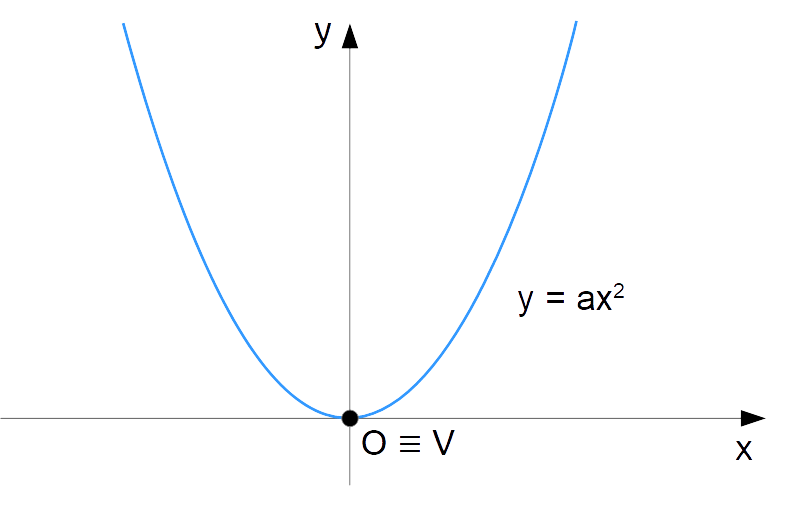
Poiché la parabola ha asse di simmetria verticale ed ha vertice nell’origine, l’asse di simmetria stesso coincide con l’asse {y}. Infatti, l’equazione dell’asse di simmetria per una generica parabola con asse verticale:

x=-\dfrac{b}{2a}

si riduce in questo caso a:

x=0

che è l’equazione dell’asse {y}. Infatti per una parabola con vertice nell’origine si ha {b=0}.

Nota: osserviamo che l’espressione {a=\dfrac{1}{4y_F}} richiede la condizione {y_F \neq 0}. Ma tale condizione è sicuramente soddisfatta poiché in una parabola con asse verticale il vertice e il fuoco non hanno mai la stessa ordinata.

Ora, dal confronto dell’equazione {y=ax^2} con l’equazione di una parabola con asse verticale e vertice in un punto arbitrario, ovvero con l’equazione {y=ax^2+bx+c} si ha:

b=0, \: c = 0

per cui possiamo affermare che a partire dall’equazione di una parabola con asse verticale, ponendo {b=0} e {c=0} otteniamo l’equazione di una parabola con vertice nell’origine degli assi.

Osserviamo infine che la particolare forma che assume il coefficiente {a} nel caso di una parabola con asse verticale e centro nell’origine, ovvero:

a=\dfrac{1}{4y_F}

si può ritrovare a partire dalla forma del coefficiente {a} per una generica parabola con asse verticale, tenendo conto che se il vertice è nell’origine si ha {d=-y_F}:

a=\dfrac{1}{2(y_F-d)}=\dfrac{1}{2[(y_F-(-y_F)]}=\dfrac{1}{2 \cdot2y_F}=\dfrac{1}{4y_F}

Con ragionamenti del tutto simili a quelli sin qui visti, è possibile inoltre ricavare l’equazione di una parabola con asse orizzontale e con vertice nell’origine:

\boxed{x=ay^2}, \qquad a \neq 0, \quad a \in \R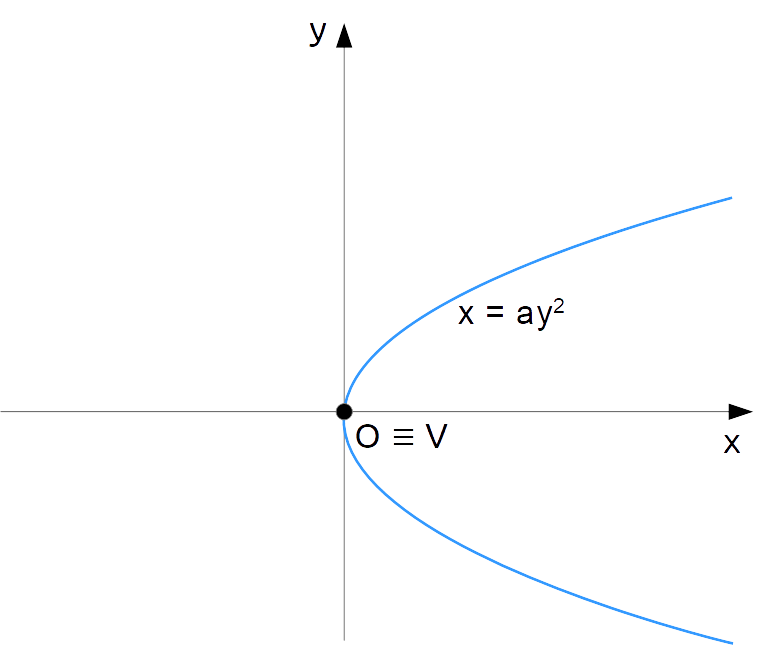

Poiché la parabola ha asse di simmetria orizzontale ed ha vertice nell’origine, l’asse di simmetria stesso coincide con l’asse {x}. Infatti, l’equazione dell’asse di simmetria di una generica parabola con asse orizzontale, ovvero l’equazione:

y=-\dfrac{b}{2a}

si riduce in questo caso a:

y=0

che è l’equazione dell’asse delle {x}. Infatti per una parabola con vertice nell’origine si ha {b=0}.

Parabola passante per l’origine

Se una parabola è passante per l’origine, un punto della parabola deve necessariamente coincidere con l’origine. Di conseguenza, l’origine {O=(0,0)} dovrà soddisfare la condizione di appartenenza alla parabola.

Considerando ad esempio il caso di una parabola con asse verticale:

y=ax^2+bx+c, \qquad a \ne0, \quad a,b,c \in \R

Se richiediamo che questa passi per l’origine, dovremo sostituire nella sua equazione i valori:

x=0, \: y = 0

ovvero dovremo sostituire nell’equazione le coordinate dell’origine. Si ottiene:

0=a \cdot 0^2+ b \cdot 0 + c \quad \Rightarrow \quad c=0

Di conseguenza, è possibile ottenere l’equazione di una parabola con asse verticale passante per l’origine ponendo {c=0} nell’equazione {y=ax^2+bx+c}. Abbiamo quindi l’equazione:

\boxed{y=ax^2+bx}, \quad a\neq0, \quad a,b \in \R

che rappresenta l’equazione di una parabola con asse verticale e passante per l’origine.

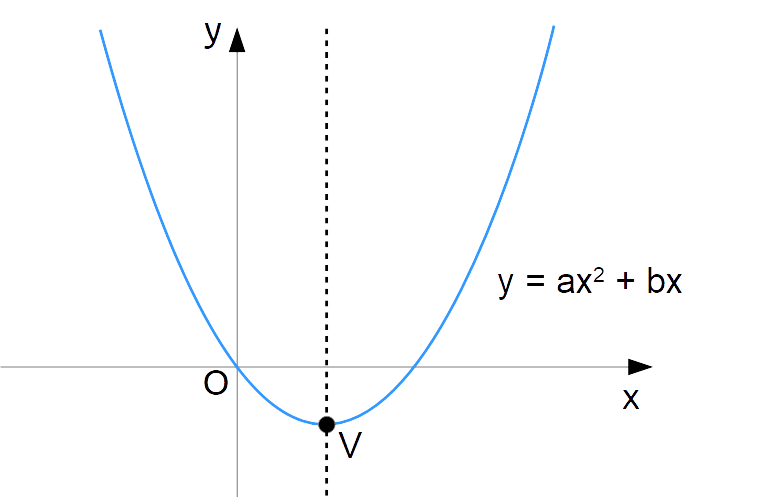
Con ragionamenti del tutto simili, è possibile infine ottenere l’equazione di una parabola con asse orizzontale e passante per l’origine:

\boxed{x=ay^2+by}, \quad a \neq0, \quad a,b \in \R

Parabola con vertice appartenente ad un asse coordinato

Consideriamo una parabola con asse di simmetria verticale. Supponiamo di voler imporre la condizione che il vertice appartenga all’asse {y}. Ricordiamo che l’asse {y} ha equazione:

x=0

Di conseguenza, richiedere che il vertice appartenga all’asse delle {y} equivale a richiedere che la sua ascissa sia uguale a zero.

Così, ricordando la formula per l’ascissa del vertice di una parabola con asse verticale, si ha:

-\dfrac{b}{2a}=0

Tale uguaglianza, valida per {a \neq 0}, è soddisfatta se e solo se:

b=0

Di conseguenza, l’equazione di una parabola con asse verticale e vertice nell’asse {\boldsymbol{y}} si ottiene a partire dall’equazione di una generica parabola con asse verticale ponendo {b=0} ed è data da:

\boxed{y=ax^2+c}, \qquad a \neq0, \quad a,c  \in \R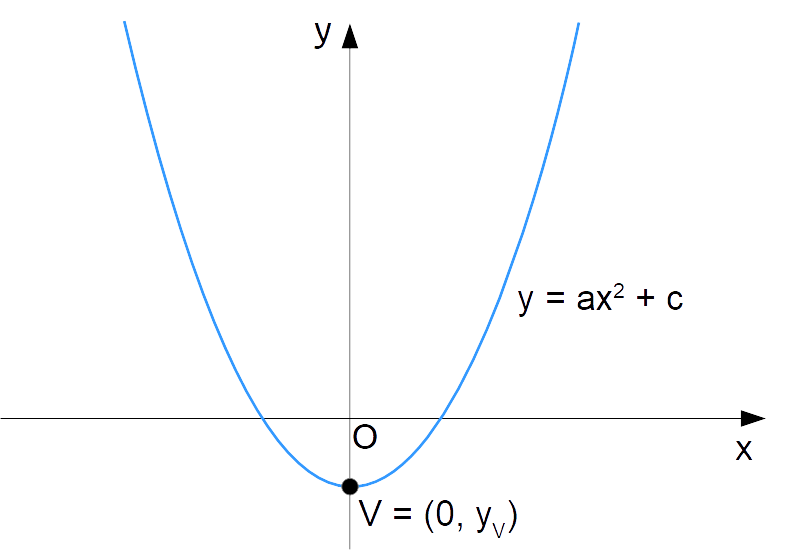

Con ragionamenti del tutto simili, l’equazione di una parabola con asse orizzontale e vertice nell’asse {\boldsymbol{x}} è data da:

\boxed{x=ay^2+c}, \qquad a\ne0, \quad a,c \in \R

Metodo alternativo per ricavare l’equazione di una parabola con vertice nell’origine

All’inizio della lezione abbiamo visto come ricavare l’equazione di una parabola con vertice nell’origine riadattando la definizione di parabola come luogo geometrico al caso dato. Vogliamo ora mostrare come ricavare l’equazione di una parabola con vertice nell’origine utilizzando un metodo alternativo. Considereremo il caso di una parabola con asse di simmetria verticale, ma il ragionamento è facilmente adattabile ad una parabola con asse di simmetria orizzontale.

Ricordiamo che il vertice di una parabola con asse di simmetria verticale, ovvero di una parabola avente equazione {y=ax^2+bx+c}, è esprimibile come:

V=\left( -\dfrac{b}{2a}, -\dfrac{\Delta}{4a}\right)

ove {\Delta = b^2-4ac}.

Ora, se richiediamo che la parabola debba avere vertice {V=(0,0)}, per la precedente si ha:

-\dfrac{b}{2a}=0, \quad -\dfrac{\Delta}{4a}=0

Poiché tali condizioni sulle coordinate del vertice devono valere contemporaneamente, l’idea è quella di impostare il sistema (esplicitiamo il {\Delta}):

\begin{cases} -\dfrac{b}{2a}=0 \\ \\ -\dfrac{b^2-4ac}{4a}=0\end{cases}

Ci ritroviamo con la difficoltà che il sistema è in due equazioni ma in tre incognite. Tuttavia, poiché una parabola con vertice nell’origine è comunque una parabola che passa per l’origine, per quanto visto nel paragrafo precedente dovrà essere:

c=0

Per cui in questo modo possiamo eliminare un’incognita nel sistema, che si riduce a:

\begin{cases} -\dfrac{b}{2a}=0 \\ \\ -\dfrac{b^2}{4a}=0\end{cases}

Ora il sistema è in due equazioni e due incognite, e possiamo di conseguenza provare a risolverlo. Il sistema è di tipo non lineare, e possiamo riscriverlo come segue:

\begin{cases} -\dfrac{1}{2a} \cdot b = 0 \\ \\ -\dfrac{1}{4a}\cdot b^2 = 0\end{cases}

Applicando la legge di annullamento del prodotto rispetto alla prima equazione a sistema, per quanto visto sulla lezione sui sistemi non lineari del link precedente abbiamo:

\begin{cases} -\dfrac{1}{2a}=0 \\ \\ -\dfrac{1}{4a} \cdot b^2 =0\end{cases} \quad \vee \quad \begin{cases} b=0 \\ \\ -\dfrac{1}{4a} \cdot b^2 =0\end{cases}

Applicando di nuovo la legge di annullamento del prodotto alla seconda equazione di ciascuno dei sistemi appena scritti ci ritroviamo in conclusione con i sistemi:

\small \begin{cases} -\dfrac{1}{2a}=0 \\ \\ -\dfrac{1}{4a}=0\end{cases} \quad \vee \quad\begin{cases} -\dfrac{1}{2a}=0 \\ \\b^2=0\end{cases} \quad \vee \quad \begin{cases} b=0 \\ \\ -\dfrac{1}{4a}=0\end{cases} \quad \vee \quad\begin{cases} b=0 \\ \\ b^2=0\end{cases}

I primi tre sistemi sono tutti impossibili. Ciascuno di essi infatti contiene delle equazioni nella variabile {a} che sono impossibili. L’unico sistema determinato è il quarto, che offre la soluzione {b=0}.

Così in conclusione, imponendo che il vertice appartenga all’origine otteniamo entrambe le condizioni {b=0} e contemporaneamente {c=0} (quest’ultima condizione è stata imposta per risolvere il sistema). Di conseguenza, ritroviamo per una parabola con asse verticale e vertice nell’origine l’equazione {y=ax^2}.

In modo del tutto simile è infine possibile ritrovare l’equazione di una parabola con asse orizzontale e vertice nell’origine, per la quale devono ancora valere contemporaneamente le condizioni {b=0} e {c=0}. Ritroviamo quindi conferma del fatto che l’equazione di una parabola con asse orizzontale e vertice nell’origine è {x=ay^2}.

Il metodo appena presentato è concettualmente non certo complicato, tuttavia richiede un po’ di dimestichezza con i sistemi non lineari. Per cui, a voi la scelta del metodo che ritenete più comodo per ricavare l’equazione di una parabola con vertice nell’origine, tenendo conto, come sempre, delle indicazioni del vostro insegnante.

Formule per le parabole con vertice nell’origine e passanti per l’origine

Vogliamo ora mostrare come si riducono le formule per il calcolo delle coordinate del fuoco e per la determinazione dell’equazione della direttrice e dell’asse di simmetria nel caso di parabole con vertice nell’origine o comunque passanti per l’origine.

Precisiamo che è comunque possibile utilizzare le stesse formule viste per le generiche parabole con asse di simmetria verticale ed orizzontale nelle lezioni precedenti. Le formule che ricaveremo a seguire risultano comunque più comode, tuttavia non è strettamente necessario impararle a memoria. L’importante è in ogni caso non fare confusione e distinguere sempre con sicurezza le formule relative ai casi generali e quelle soltanto valevoli per casi specifici.

Nei casi di parabole passanti per l’origine e con vertice appartenente ad uno degli assi coordinati non conviene invece ricavare della formule specifiche. In questi casi continueremo dunque ad avvalerci delle formule generali viste nelle lezioni precedenti.

Parabole con vertice nell’origine

Per le parabole con vertice nell’origine abbiamo {b=0} e {c=0}. Di conseguenza, le seguenti formule, valevoli per una generica parabola con asse di simmetria verticale:

\begin{align*} & F=\left( -\dfrac{b}{2a}, \dfrac{1-(b^2-4ac)}{4a}\right); \qquad s: y=-\dfrac{1+b^2-4ac}{4a}; \\ \\ & x=-\dfrac{b}{2a} \qquad \text{(asse di simmetria)} \end{align*}

si riducono a:

\begin{align*}&F=\left( 0, \dfrac{1}{4a}\right); \qquad s:y=-\dfrac{1}{4a};  \\ \\ & x=0  \qquad \text{asse di simmetria}\\ \\ & \small{\textbf{(formule per parabole con vertice nell'origine ed asse di simmetria verticale)}}\end{align*}

Inoltre, ricordiamo che in questo caso il coefficiente {a} relativo all’equazione della parabola è esprimibile come:

a=\dfrac{1}{4y_F}; \qquad \small \text{(parabola con asse verticale e vertice nell'origine)}

Basta comunque osservare che dalla precedente formula delle coordinate del fuoco si ha {y_F=\dfrac{1}{4a}}, da cui segue la formula per il coefficiente {a} appena scritta.

Con ragionamenti del tutto simili, dette formule nel caso di parabole con asse di simmetria orizzontale e vertice nell’origine si riducono a:

\begin{align*} &F=\left( \dfrac{1}{4a}, 0\right); \qquad s: x=-\dfrac{1}{4a};\\ \\ & y=0 \qquad \text{asse di simmetria}\\ \\ & \small \textbf{(formule per parabole con vertice nell'origine ed asse di simmetria orizzontale)}\end{align*}

Infine, ricordiamo che in questo caso, come visto in precedenza, il coefficiente {a} relativo all’equazione della parabola è esprimibile come:

a=\dfrac{1}{4x_F}; \qquad \small \text{(parabola con asse orizzontale e vertice nell'origine)}

Anche in questa circostanza è comunque immediato riconfermare tale risultato. Basta infatti osservare che dalla precedente formula delle coordinate del fuoco si ha {x_F=\dfrac{1}{4a}}, da cui segue la formula per il coefficiente {a} appena scritta.

Vediamo ora un paio di esempi.

Esempio 1

Scrivere l’equazione di una parabola con vertice nell’origine avente fuoco {F=(0,-5)}. Scrivere inoltre l’equazione della sua direttrice.

Osserviamo che poiché la parabola ha vertice nell’origine, l’ascissa del fuoco e l’ascissa del vertice coincidono. Di conseguenza, la parabola ha asse di simmetria verticale che coincide con l’asse {y}. Pertanto ci ritroviamo con una parabola con asse di simmetria verticale e vertice nell’origine.

Per scrivere l’equazione della parabola basta ricavare il coefficiente {a}:

a=\dfrac{1}{4y_F}=\dfrac{1}{4 \cdot (-5)}=-\dfrac{1}{20}

da cui segue l’equazione della parabola in esame:

y=-\dfrac{1}{20}x^2

Per l’equazione della direttrice si ha infine:

s: y=-y_F \quad \Rightarrow \quad s:y=5

Osservazione. Una parabola con vertice nell’origine è univocamente determinata una volta nota soltanto l’ordinata del fuoco (se la parabola è ad asse verticale) o l’ascissa del fuoco (se la parabola è ad asse orizzontale). Infatti, per scriverne l’equazione è necessario il solo coefficiente {a}, che è funzione unicamente dell’ordinata o dell’ascissa del fuoco, a seconda che l’asse della parabola sia rispettivamente verticale od orizzontale.

Esempio 2

Determinare coordinate del fuoco, equazione della direttrice ed equazione dell’asse di simmetria della parabola di equazione {x=3y^2}.

Dall’equazione segue immediatamente {a=5}. Osserviamo che l’equazione è del tipo {x=f(y)} e quindi ci ritroviamo con una parabola con asse di simmetria orizzontale. Inoltre essendo {b=0} e {c=0} la parabola ha vertice nell’origine.

Per le coordinate del fuoco abbiamo:

F=\left( \dfrac{1}{4a}, 0\right)=\left(\dfrac{1}{4 \cdot 3}, 0 \right)=\left( \dfrac{1}{12}, 0\right)

mentre per l’equazione della direttrice si ha:

x=-\dfrac{1}{4a} \quad \Rightarrow \quad x=-\dfrac{1}{4 \cdot 3} \quad \Rightarrow \quad s: x=-\dfrac{1}{12}

Infine, per l’asse di simmetria:

y=0

Conclusioni

Per questa lezione sulla parabola con vertice nell’origine, passante per l’origine e con vertice in uno dei due assi coordinati è tutto. Nella prossima lezione ci occuperemo del problema delle rette tangenti ad una parabola.

Un saluto a tutti voi e buon proseguimento con SìMatematica!