Parabola con asse orizzontale

 - 

Parabola (scuole superiori)

L’equazione di una parabola con asse di simmetria orizzontale è data da {x = ay² + by + c}, con a, b, c coefficienti reali e a ≠ 0. La direttrice della parabola è verticale (perpendicolare all’asse di simmetria) e la concavità è rivolta verso la direzione positiva dell’asse delle x se a > 0 e verso la direzione negativa dell’asse delle x se a < 0.

Dopo aver visto nel dettaglio il caso della parabola con asse verticale, in questa lezione ci occupiamo del caso relativo alla parabola con asse di simmetria orizzontale (o, più brevemente, parabola con asse orizzontale).

In questa lezione vedremo in particolare come determinare l’equazione di una parabola con asse orizzontale a partire dalle coordinate di un certo punto denominato fuoco e dalla distanza con segno che ha la direttrice rispetto all’asse delle x. Viceversa, vedremo anche come sia possibile ricavare le coordinate del fuoco, del vertice e l’equazione della direttrice a partire dall’equazione di una data parabola.

Ci occuperemo poi nel dettaglio del concetto di concavità di una parabola con asse orizzontale, mostrando i casi nei quali la concavità risulta rivolta verso la direzione positiva oppure negativa dell’asse delle x.

Nel corso della lezione ci concentreremo sulle varie formule riguardanti la parabola con asse orizzontale ed i relativi esempi di utilizzo, mentre soltanto alla fine della lezione forniremo le dimostrazioni delle formule più importanti. Con ciò, come già fatto nella precedente lezione, integreremo le nozioni già esposte a suo tempo nella lezione introduttiva sulla parabola, ma nell’ambito di un approccio più mirato e graduale.

Equazione di una parabola con asse orizzontale

L’equazione di una parabola con asse di simmetria orizzontale è data da:{x=ay^2+by+c}con {a,b,c} coefficienti reali e con {a \neq 0}.

E’ importante osservare che l’equazione è della forma {x=f(y)}, e non della forma {y=f(x)} come nel caso di una parabola con asse di simmetria verticale. In particolare, al primo membro non abbiamo più la {y} ma la {x}, e al secondo membro non abbiamo più un’espressione funzione della variabile {x}, ma piuttosto della variabile {y}.

L’equazione discende direttamente dalla definizione di parabola come luogo geometrico.

La parabola è il luogo geometrico di punti del piano tali che ciascun punto presenta la medesima distanza rispetto ad una particolare retta {s} detta direttrice e rispetto ad un fissato punto {F} detto fuoco, non appartenente alla direttrice.

Nel caso di una parabola con asse orizzontale, la direttrice è una retta verticale. Si tratta quindi di una retta avente equazione della forma:

s: x=d, \qquad d \in \R

ove {d} è l’ascissa in comune a tutti i punti della direttrice, che può essere anche vista come la distanza con segno della direttrice rispetto all’asse {y}.

Importante. Secondo le convenzioni qui adottate indichiamo con {s} la direttrice e con {d} il valore al secondo membro dell’equazione della direttrice.

Il fuoco è un punto che può essere scelto arbitrariamente, ma a patto che non appartenga alla direttrice:

F=(x_F, y_F), \qquad x_F \neq d, \quad x_F, \: y_F \in \R

Osserviamo che poiché i punti della direttrice hanno tutti ascissa {d}, affermare che il fuoco non appartiene alla direttrice equivale ad affermare che la sua ascissa è diversa da {d}, da cui la condizione {x_F \neq d}.

Una volta scelti il fuoco {F} e la direttrice {s}, la parabola risulta determinata, e può essere disegnata tenendo conto della sua definizione come luogo geometrico. In particolare, la parabola sarà data da tutti i punti {P=(x,y)} del piano tali da avere la stessa distanza dal fuoco e dalla direttrice.

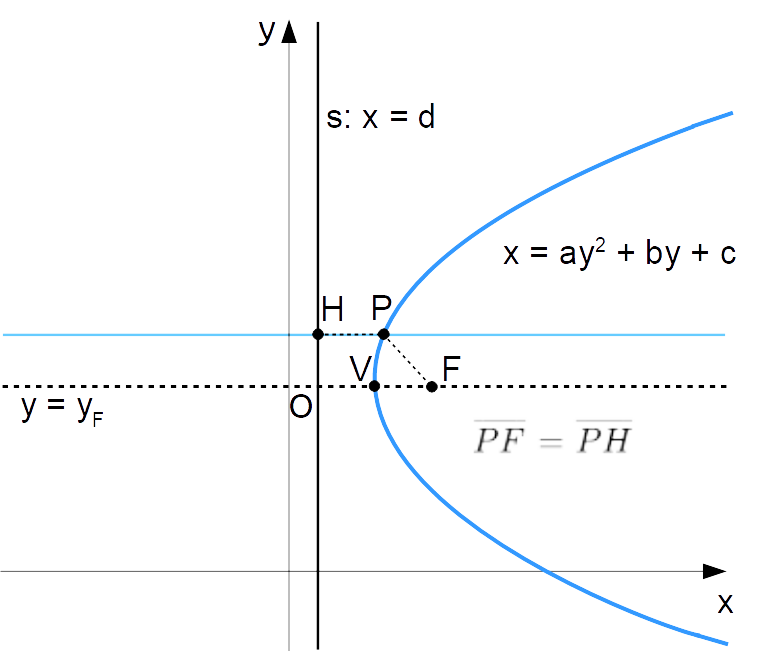
Il punto {H} è determinato dall’intersezione tra la direttrice {s} e la retta orizzontale passante per il punto {P}. Osserviamo che la distanza {\overline{PH}} coincide con la distanza tra la retta direttrice e il punto {P}. Inoltre, la distanza tra il generico punto {P=(x,y)} della parabola e il fuoco {F} è data da {\overline{PF}}.

Così, utilizzando tali distanze, dalla definizione di parabola come luogo geometrico discende l’uguaglianza:

\overline{PH}=\overline{PF}

ed è proprio da tale uguaglianza, come vedremo alla fine della lezione, che si ottiene l’equazione della parabola con asse di simmetria orizzontale. Tra l’altro, l’approccio è del tutto simile a quello già visto per il caso di una parabola con asse di simmetria verticale.

Per concludere, l’asse di simmetria della parabola in esame ha equazione:

y=y_F

ed effettivamente è una retta orizzontale. Osserviamo che la direttrice e l’asse di simmetria di una parabola sono tra loro perpendicolari.

Come determinare l’equazione di una parabola con asse orizzontale a partire dalle coordinate del fuoco e dall’equazione della direttrice

Siano date le coordinate del fuoco e l’equazione della direttrice di una parabola con asse di simmetria orizzontale:

F=(x_F, y_F), \qquad s:x=d

E’ possibile scrivere l’equazione della parabola avente per fuoco il punto {F} e per direttrice la retta {s} calcolando i coefficienti {a,b,c} dell’equazione della parabola mediante le formule:

a=\dfrac{1}{2(x_F-d)}; \qquad b=-\dfrac{y_F}{x_F-d}; \qquad c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)} \qquad (*)

Le formule discendono dalla definizione di parabola come luogo geometrico e rappresentano delle sostituzioni che consentono di scrivere in forma compatta l’equazione della parabola stessa.

Nel nostro caso, le formule risultano particolarmente utili poiché consentono di determinare i coefficienti {a,b,c} a partire dalle coordinate del fuoco e dall’equazione della direttrice, permettendo così di scrivere l’equazione di una parabola con asse orizzontale nella forma {x=ay^2+by+c}.

Esempio 1

Scrivere l’equazione della parabola con asse di simmetria orizzontale avente fuoco {F=(-3,5)} ed equazione della direttrice {x=-7}. Determinare infine l’equazione dell’asse di simmetria.

Poiché è {F=(-3,5)} abbiamo {x_F=-3} ed {y_F=5}. Inoltre, dato che l’equazione della direttrice è {x=-7}, abbiamo per {d} il valore {-7}.

Possiamo a questo punto calcolare i coefficienti {a,b,c} necessari a scrivere l’equazione della parabola tramite le *:

\begin{align*} &a=\dfrac{1}{2(x_F-d)}=\dfrac{1}{2 \cdot[-3-(-7)]}=\dfrac{1}{2 \cdot4}=\dfrac{1}{8}; \\ \\  &b=-\dfrac{y_F}{x_F-d}=-\dfrac{5}{-3-(-7)}=-\dfrac{5}{4} \\ \\ &c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)}=\dfrac{(-3)^2+5^2-(-7)^2}{2[-3-(-7)]}=\dfrac{9+25-49}{8}=-\dfrac{15}{8}\end{align*}

Così l’equazione della parabola in esame si ottiene sostituendo i valori appena calcolati per i coefficienti {a,b,c} nella generica equazione di una parabola ad asse orizzontale:

x=ay^2+by+c

ottenendo:

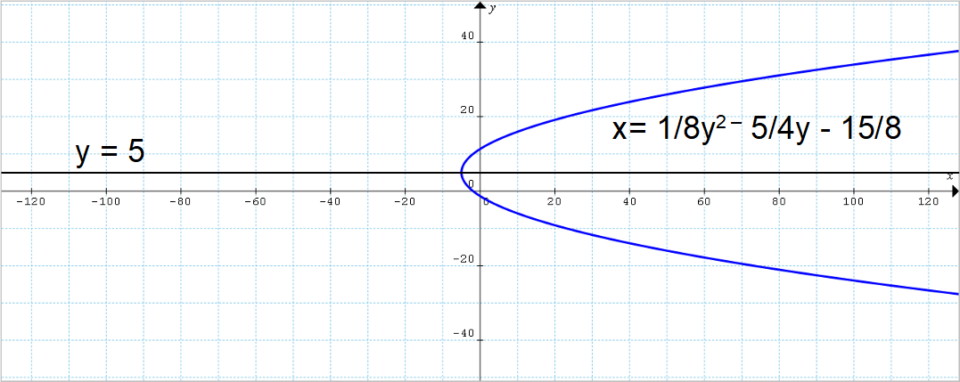
x=\dfrac{1}{8}y^2-\dfrac{5}{4}y-\dfrac{15}{8}

Infine, l’asse di simmetria ha equazione {y=y_F} e quindi nel nostro caso:

y=5

Coordinate del fuoco e del vertice, equazioni dell’asse di simmetria e della direttrice di una parabola con asse orizzontale a partire dalla sua equazione

Vediamo ora come determinare le coordinate del fuoco, del vertice ed inoltre le equazioni dell’asse di simmetria e della direttrice di una parabola con asse orizzontale a partire dalla sua equazione. In particolare, ciò che utilizzeremo sono i valori dei coefficienti {a,b,c} presenti nell’equazione fornita dal testo del problema.

Supponiamo allora di avere l’equazione di una parabola con asse orizzontale:

x=ay^2+by+c, \qquad a \neq 0, \quad a,b,c \in \R

Per determinare le coordinate del fuoco e del vertice, nonché le equazioni dell’asse di simmetria e della direttrice è possibile utilizzare delle formule contenenti delle espressioni in funzione dei coefficienti {a,b,c} dell’equazione della parabola.

In particolare, per una parabola con asse di simmetria orizzontale le coordinate del fuoco sono date da:

F=\left( x_F, y_F\right)=\left( \dfrac{1-\Delta}{4a},  -\dfrac{b}{2a}\right)

ove {\Delta = b^2-4ac} è una quantità a noi già nota, ovvero il discriminante relativo alle equazioni di secondo grado. Osserviamo che le coordinate risultano scambiate fra loro rispetto alla coordinate del fuoco di una parabola con asse verticale.

Le coordinate del vertice di una parabola con asse di simmetria orizzontale sono invece date da:

V=(x_V, y_V)=\left( -\dfrac{\Delta}{4a},  -\dfrac{b}{2a}\right)

Anche in questo caso, osserviamo che le coordinate risultano scambiate fra loro rispetto a quelle relative al vertice di una parabola con asse verticale.

Infine, l’equazione della direttrice della parabola (sempre con asse orizzontale) è:

s:x=-\dfrac{1+\Delta}{4a}

mentre l’equazione dell’asse di simmetria è:

y=-\dfrac{b}{2a}

in quanto effettivamente dalla formula delle coordinate del fuoco si ha {y_F=-\dfrac{b}{2a}}.

Una parabola con asse orizzontale di equazione {x=ay^2+by+c} ha coordinate del fuoco e del vertice esprimibili come:{\begin{align*} &F=\left(\dfrac{1-\Delta}{4a}, -\dfrac{b}{2a}\right); \qquad V=\left( -\dfrac{\Delta}{4a}, -\dfrac{b}{2a}\right)\end{align*}}ove {\Delta=b^2-4ac}.

L’equazione della direttrice {s} e l’equazione dell’asse di simmetria si determinano infine come:{\begin{align*} & s: x=-\dfrac{1+ \Delta}{4a} \qquad \text{direttrice}; \\ \\ & y=-\dfrac{b}{2a} \qquad \text{asse di simmetria}\end{align*}}

A questo punto è opportuno fare delle osservazioni del tutto simili a quelle già viste a suo tempo per le parabole con asse di simmetria verticale.

Osserviamo che in una parabola con asse orizzontale fuoco e vertice condividono la stessa ordinata. Entrambi infatti giacciono sull’asse di simmetria (vedi una precedente figura). Inoltre, l’ascissa del vertice può anche essere calcolata sostituendo il valore dell’ordinata del fuoco (e quindi del vertice) nell’equazione della parabola.

Le formule appena scritte relative alle coordinate del fuoco e all’equazione della direttrice si ottengono ribaltando le *. La formula per l’ascissa del vertice si ottiene invece sostituendo nell’equazione di una generica parabola con asse orizzontale l’espressione {-\dfrac{b}{2a}} relativa all’ordinata del fuoco (e quindi all’ordinata del vertice). Infatti il vertice è un punto che appartiene alla parabola.

L’equazione dell’asse di simmetria è infine data dall’equazione della retta orizzontale passante per il fuoco e per il vertice.

Consideriamo ora un esempio su come determinare le coordinate del fuoco e del vertice e le equazioni della direttrice e dell’asse di simmetria di una parabola con asse orizzontale, a partire dalla sua equazione.

Esempio 2

Determinare le coordinate del fuoco e del vertice ed inoltre le equazioni della direttrice e dell’asse di simmetria di una parabola con asse di simmetria orizzontale avente equazione {x=5y^2-3y+4}.

Confrontiamo l’equazione data con l’equazione di una generica parabola con asse di simmetria orizzontale:

x=ay^2+by+c

Dal confronto abbiamo {a=5, b=-3, c=4}.

Cominciamo calcolando il discriminante {\Delta}:

\Delta = b^2-4ac = (-3)^2-4 \cdot 5 \cdot 4 = 9-80=-71

Per le coordinate del fuoco abbiamo:

\small F=\left( \dfrac{1-\Delta}{4a}, -\dfrac{b}{2a}\right)=\left( \dfrac{1-(-71)}{4 \cdot 5}, -\dfrac{-3}{2\cdot5}\right)=\left( \dfrac{72}{20}, \dfrac{3}{10}\right)=\left( \dfrac{18}{5}, \dfrac{3}{10}\right)

Per le coordinate del vertice:

V=\left( -\dfrac{\Delta}{4a}, -\dfrac{b}{2a}\right)=\left( -\dfrac{-71}{4\cdot5}, \dfrac{3}{10}\right)=\left( \dfrac{71}{20}, \dfrac{3}{10}\right)

Osserviamo che non è stato necessario calcolare l’ordinata del vertice poiché questa coincide con l’ordinata del fuoco, che abbiamo già calcolato in precedenza.

Se non si ricorda la formula dell’ascissa del vertice di una parabola con asse orizzontale, è anche possibile in alternativa sostituire l’ordinata del vertice (e quindi del fuoco) nell’equazione della parabola:

\begin{align*} &x_V=5y_V^2-3y_V+4=5 \cdot \left( \dfrac{3}{10}\right)^2-3 \cdot\dfrac{3}{10}+4=\\ \\ & =5 \cdot \dfrac{9}{100}-\dfrac{9}{10}+4=\dfrac{45-90+400}{100}=\dfrac{355}{100}=\dfrac{71}{20}\end{align*}

Ritroviamo correttamente, anche in questo modo, l’ascissa del vertice della parabola, sebbene con più calcoli.

Ora, procediamo determinando l’equazione della direttrice {s}:

s: x = -\dfrac{1+\Delta}{4a}

Si ha:

-\dfrac{1+\Delta}{4a}=-\dfrac{1+(-71)}{4 \cdot 5}=-\dfrac{-70}{20}=\dfrac{70}{20}=\dfrac{7}{2}

da cui:

s: x=\dfrac{7}{2}

Infine per l’asse di simmetria:

y=y_F \quad \Rightarrow \quad y=\dfrac{3}{10}

Concavità di una parabola con asse di simmetria parallelo all’asse x

La concavità di una parabola dipende in generale dalla posizione del fuoco rispetto alla direttrice. Nel caso di una parabola con asse di simmetria orizzontale (asse di simmetria parallelo all’asse {x}), se il fuoco si trova a destra della direttrice, la parabola rivolge la propria concavità verso la direzione positiva dell’asse delle {x}, viceversa se il fuoco si trova a sinistra della direttrice, la parabola rivolge la propria concavità verso la direzione negativa dell’asse delle {x}.

Ciò è una diretta conseguenza della definizione di parabola come luogo geometrico.

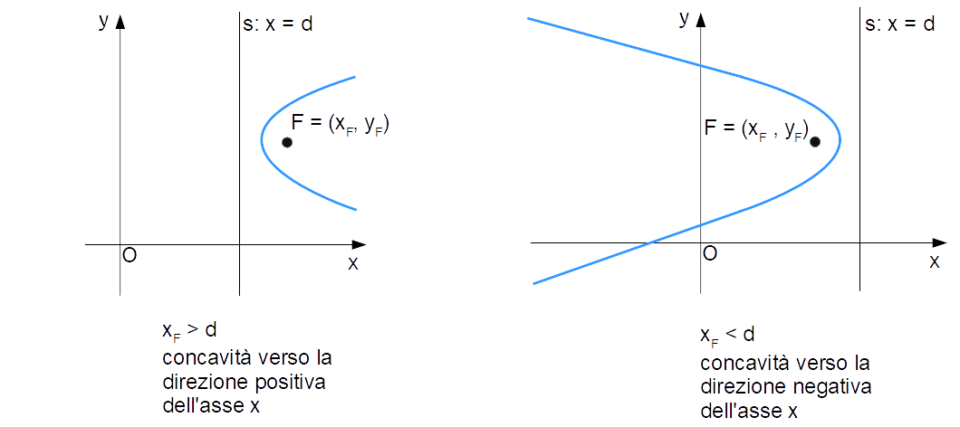
Come mostrano le figure, la posizione del fuoco rispetto alla direttrice è determinata dall’ascissa del fuoco {x_F}. In particolare, se {x_F > d} la concavità della parabola è rivolta verso la direzione positiva dell’asse delle {x}, mentre se {x_F < d} la concavità della parabola è rivolta verso la direzione negativa dell’asse delle {x}.

Ora, quello che a noi interessa è trovare un modo rapido per stabilire, a partire dall’equazione di una parabola con asse orizzontale, se questa rivolge la propria concavità verso la direzione positiva oppure negativa dell’asse delle {x}. Le relazioni {x_F > d} e {x_F < d} risultano piuttosto scomode, poiché richiedono di calcolare l’ascissa del fuoco {x_F} e la quantità {d}.

Ma per le formule introdotte in precedenza, osserviamo che si ha:

x_F=\dfrac{1-\Delta}{4a}, \qquad d=-\dfrac{1+\Delta}{4a}

Così è possibile riscrivere ad esempio la disuguaglianza {x_F> d}, riguardante il caso della parabola con concavità rivolta verso la direzione positiva dell’asse delle {x}, in funzione dei soli coefficienti presenti nell’equazione della parabola stessa. Ed in particolare, è possibile vedere che procedendo in questo modo otteniamo una relazione contenente il solo coefficiente {a}. Nello specifico, dalla condizione {x_F > d} segue la condizione {a>0}.

Allo stesso tempo, da precedenti formule si ha anche:

a=\dfrac{1}{2(x_F-d)}

da cui risulta che se {a > 0} allora deve essere anche {x_F > d}.

Quindi in conclusione, se {a > 0}, ovvero se {a} è positivo, la concavità di una parabola con asse orizzontale è rivolta verso la direzione positiva dell’asse {x}. Viceversa, se la concavità di una parabola con asse orizzontale è rivolta verso la direzione positiva dell’asse {x}, allora si ha come conseguenza {a > 0}.

In modo del tutto simile, è possibile concludere che se {a <0 }, ovvero se {a} è negativo, la concavità di una parabola con asse orizzontale è rivolta verso la direzione negativa dell’asse delle {x}. Viceversa, se la concavità di una parabola è rivolta verso la direzione negativa dell’asse delle {x}, allora {a} è negativo.

Possiamo quindi affermare quanto segue.

La concavità di una parabola con asse di simmetria orizzontale è rivolta verso la direzione positiva dell’asse x se e solo se il coefficiente {a} della corrispondente equazione è positivo, mentre è rivolta verso la direzione negativa dell’asse delle x se e solo se il coefficiente {a} è negativo.

E’ dunque possibile stabilire verso quale direzione è rivolta la concavità di una parabola con asse orizzontale effettuando una rapida osservazione della sua equazione. Ciò è del tutto simile a quanto visto per le parabola con asse verticale.

In particolare, per dedurre la concavità di una parabola con asse orizzontale dobbiamo guardare il segno del termine in {y^2}.

Allo stesso tempo, osservando il grafico di una parabola con asse orizzontale, se questa ha concavità rivolta verso la direzione positiva dell’asse x, il coefficiente {a} della sua equazione dovrà essere necessariamente positivo. Se invece abbiamo il grafico di una parabola con concavità rivolta verso la direzione negativa dell’asse x, il coefficiente {a} della corrispondente equazione dovrà essere necessariamente negativo.

Esempio 3

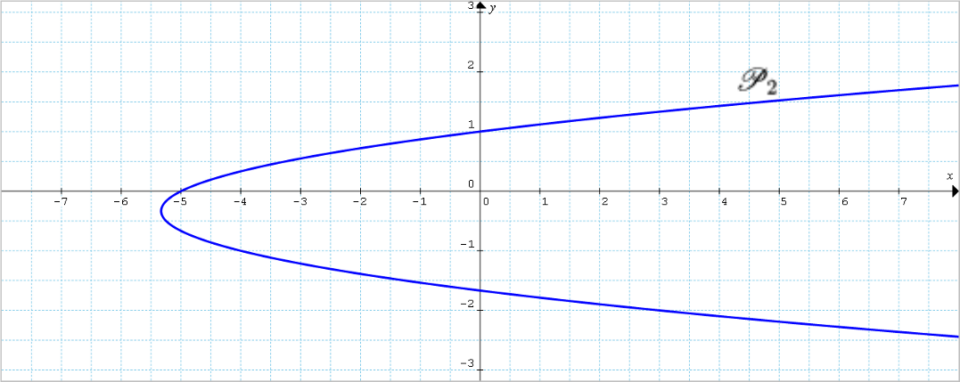
Discutere la concavità delle parabole {\mathscr{P}_1: x=-5y^2+3y+6} e {\mathscr{P}_2: x=3y^2+2y-5}.

La parabola {\mathscr{P}_1} ha coefficiente del termine di secondo grado negativo ({a < 0}) e quindi rivolge la propria concavità verso la direzione negativa dell’asse delle {x}:

La parabola {\mathscr{P}_2} ha invece coefficiente del termine di secondo grado positivo ({a > 0}) e quindi rivolge la propria concavità verso la direzione positiva dell’asse delle {x}:

Dimostrazioni relative alla parabola con asse orizzontale

Vediamo ora le dimostrazioni delle principali formule relative alla parabola con asse orizzontale. In particolare, forniremo la dimostrazione dell’equazione di una parabola con asse orizzontale e delle formule per ricavare le coordinate del fuoco e del vertice e per determinare le equazioni dell’asse di simmetria e della direttrice.

Le dimostrazioni sono le stesse che abbiamo già visto nella lezione introduttiva sulla parabola, ma in questa lezione commenteremo più nel dettaglio ciascun passaggio.

Dimostrazione dell’equazione di una parabola con asse orizzontale

Per svolgere la dimostrazione dell’equazione di una parabola con asse orizzontale, il punto di partenza è la definizione di parabola come luogo geometrico.

Ricordiamo anzitutto che l’equazione di una parabola con asse orizzontale è:

x=ay^2+by+c, \qquad a \neq 0, \quad a,b,c \in \R

Dato un punto {P=(x,y)} appartenente alla parabola, le sue coordinate devono essere tali da soddisfare l’uguaglianza:

\overline{PF}=\overline{PH}

Ciascun membro dell’uguaglianza appena scritta rappresenta la distanza tra il punto {P} della parabola e, rispettivamente, il fuoco {F} e il punto {H}.

Osserviamo che il punto {H} si individua sulla direttrice tracciando la retta orizzontale passante per {P}, ed ha coordinate {H=(d,y)}. Inoltre, la distanza {\overline{PH}} coincide con la distanza tra il punto {P} e la direttrice {s}.

Di conseguenza, l’uguaglianza {\overline{PF}=\overline{PH}} equivale a dire che la distanza tra il punto {P} e il fuoco {F} deve essere uguale alla distanza tra il punto {P} e la direttrice, ritrovando correttamente la definizione di parabola come luogo geometrico.

Ora, utilizzando la definizione di distanza tra due punti nel piano, l’uguaglianza {\overline{PF}=\overline{PH}} diviene:

\sqrt{(x_F-x)^2+(y_F-y)^2}=\sqrt{(x_H-x)^2+(y_H-y)^2}

e quindi, tenendo conto delle coordinate del punto {H}:

\sqrt{(x_F-x)^2+(y_F-y)^2}=\sqrt{(d-x)^2+(y-y)^2}

ovvero:

\sqrt{(x_F-x)^2+(y_F-y)^2}=\sqrt{(d-x)^2}

Per le proprietà dei radicali, osserviamo che il secondo membro diviene {|d-x|}:

\sqrt{(x_F-x)^2+(y_F-y)^2}=|d-x|

Infine, per note proprietà del valore assoluto, possiamo riscrivere il secondo membro come segue:

\sqrt{(x_F-x)^2+(y_F-y)^2}=|x-d|

E’ possibile a questo punto elevare al quadrato entrambi i membri dell’uguaglianza, senza alcuna discussione. Infatti, il primo membro è positivo in quanto radice quadrata, mentre il secondo membro è positivo in quanto valore assoluto. Inoltre, il radicando al primo membro è sempre positivo in quanto somma di quadrati. Per cui, diversamente da quanto richiesto in generale dalle equazioni irrazionali, in questo caso non serve né una condizione di concordanza dei segni, né una condizione di realtà per il radicale al primo membro.

Abbiamo quindi:

(x_F-x)^2+(y_F-y)^2=(x-d)^2

Eseguiamo i prodotti e quindi i rimanenti calcoli, isolando la variabile {x}:

\begin{align*} &{x_F^2}-2x_Fx+\cancel{x^2}+y_F^2-2y_Fy+{y^2}=\cancel{x^2}-2dx+d^2; \\ \\ &2x_Fx-2dx=y^2-2y_Fy+x_F^2+y_F^2-d^2;\\ \\ & 2x(x_F-d)=y^2-2y_Fy+x_F^2+y_F^2-d^2\end{align*}

Ora proseguiamo i passaggi dividendo tutti i termini per {x_F-d}, in modo da isolare la {x}. Osserviamo che ciò richiede la condizione {x_F-d \neq 0}, ovvero {x_F \neq d}, per il secondo principio di equivalenza. Ma tale condizione è necessariamente rispettata, poiché il fuoco {F} non appartiene alla direttrice. Abbiamo quindi:

x=\dfrac{1}{2(x_F-d)}y^2-\dfrac{y_F}{x_F-d}y+\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)}

Infine, ponendo:

a=\dfrac{1}{2(x_F-d)}, \qquad b=-\dfrac{y_F}{x_F-d}, \qquad c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)}

ritroviamo in conclusione l’equazione di una parabola con asse di simmetria orizzontale:

x=ay^2+by+c

che risulta così dimostrata.

Dimostrazione delle formule delle coordinate del fuoco, del vertice e per determinare le equazioni dell’asse di simmetria e della direttrice

Cominciamo con la dimostrazione delle coordinate del fuoco e dell’equazione della direttrice di una parabola con asse di simmetria orizzontale. Allo scopo, riprendiamo le *:

a=\dfrac{1}{2(x_F-d)}, \qquad b=-\dfrac{y_F}{x_F-d}, \qquad c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)}

Dato che tali uguaglianze devono valere tutte contemporaneamente, possiamo metterle a sistema:

\begin{cases}  a=\dfrac{1}{2(x_F-d)} \\ \\  b=-\dfrac{y_F}{x_F-d} \\ \\ c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)} \end{cases}

Per risolvere il sistema, l’idea è quella di ricavare delle espressioni per le coordinate del fuoco, e quindi sostituire tali espressioni nella terza equazione, ricavando un’espressione per la distanza con segno {d} della direttrice rispetto all’asse {y}.

Ricaviamo un’espressione per {x_F} dalla prima equazione e per {y_F} dalla seconda equazione:

\begin{cases}  a=\dfrac{1}{2(x_F-d)} \quad \rightarrow \quad x_F-d=\dfrac{1}{2a} \quad \rightarrow \quad x_F=\dfrac{1}{2a}+d \\ \\  b=-\dfrac{y_F}{x_F-d} \quad \rightarrow \quad y_F=-b(x_F-d) \\ \\ c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)} \end{cases}

Osserviamo che non è necessario porre la condizione {x_F \neq d} poiché per ipotesi il fuoco non appartiene alla direttrice.

Ora sostituiamo l’espressione ottenuta per {x_F} dalla prima equazione nella seconda equazione:

\small \begin{cases}   x_F=\dfrac{1}{2a}+d \\ \\  y_F=-b(x_F-d) \quad \rightarrow \quad y_F=-b\left( \dfrac{1}{2a}+d-d\right) \quad \rightarrow \: \boxed{y_F=-\dfrac{b}{2a}} \\ \\ c=\dfrac{x_F^2+y_F^2-d^2}{2(x_F-d)} \end{cases}

Dall’espressione ottenuta per {y_F} ricaviamo tra l’altro l’equazione dell’asse di simmetria della parabola:

y=-\dfrac{b}{2a}

A questo punto sostituiamo le espressioni ottenute per {x_F} ed {y_F} nella terza equazione, che consideriamo separatamente. Cerchiamo di esplicitare la {d}:

\begin{align*} &c=\dfrac{\left( \dfrac{1}{2a}+d\right)^2+\left( -\dfrac{b}{2a}\right)^2-d^2}{2(\dfrac{1}{2a}+\cancel{d}-\cancel{d})}; \\ \\ & c=\dfrac{\dfrac{1}{4a^2}+\dfrac{d}{a}+d^2+\dfrac{b^2}{4a^2}-d^2}{\dfrac{1}{a}}; \\ \\ & c={\dfrac{1+4ad+\cancel{4a^2d^2}+b^2-\cancel{4a^2d^2}}{4a^{\cancel{2}}}}{ \cdot \cancel{a}}\end{align*}

Ora trasportiamo tutti i termini al primo membro, e quindi mettiamo tutti i termini a denominatore comune:

\begin{align*} &\dfrac{1+4ad+b^2}{4a}-c=0; \\ \\ & \dfrac{1+4ad+b^2-4ac}{4a}=0\end{align*}

Eliminiamo il denominatore ponendo la condizione {a \neq 0}. Osserviamo che tale condizione è sicuramente soddisfatta poiché nell’equazione di una parabola con asse orizzontale (o verticale) deve essere {a \neq 0}. Per cui in questo caso non è nemmeno necessario porre esplicitamente tale condizione.

1+4ad+b^2-4ac=0

Ora riconosciamo la quantità {\Delta=b^2-4ac}:

1+4ad+\Delta=0

A questo punto isoliamo la {d}:

\begin{align*} &4ad=-1-\Delta; \\ \\ & d=\dfrac{-1-\Delta}{4a}; \\ \\ & \boxed{d=-\dfrac{1+\Delta}{4a}}\end{align*}

Abbiamo così ottenuto un’espressione per la distanza con segno {d} in funzione dei soli coefficienti {a,b,c} dell’equazione della parabola con asse orizzontale, da cui segue per l’equazione della direttrice:

s: x=-\dfrac{1+\Delta}{4a}

A questo punto, sfruttando l’espressione per {d} di cui ora disponiamo possiamo aggiustare l’espressione precedentemente ottenuta per {x_F}:

x_F=\dfrac{1}{2a}+d \quad \Rightarrow \quad x_F=\dfrac{1}{2a}-\dfrac{1+\Delta}{4a} \quad \Rightarrow \quad \boxed{x_F=\dfrac{1-\Delta}{4a}}

Ora anche {x_F} è espressa in funzione dei soli coefficienti {a,b,c}.

Abbiamo così dimostrato le formule per le coordinate del fuoco e per l’equazione della direttrice di una parabola con asse di simmetria orizzontale.

Infine, per l’ascissa del vertice, osserviamo anzitutto che l’ordinata del vertice coincide, in una parabola con asse di simmetria orizzontale, con l’ordinata del fuoco:

y_V=y_F=-\dfrac{b}{2a}

Sostituendo tale espressione nell’equazione della parabola abbiamo:

\begin{align*} &x_V=a \cdot\left( -\dfrac{b}{2a}\right)^2+b\cdot\left( -\dfrac{b}{2a}\right)+c=\cancel{a} \cdot\dfrac{b^2}{4a^{\cancel{2}}}-\dfrac{b^2}{2a}+c=\\ \\ & =\dfrac{b^2-2b^2+4ac}{4a}=\dfrac{-b^2+4ac}{4a}=-\dfrac{\Delta}{4a}\end{align*}

Così le coordinate del vertice sono in conclusioni esprimibili come:

V=\left( -\dfrac{\Delta}{4a}, -\dfrac{b}{2a}\right)

Dimostrazione della condizione di concavità diretta verso la direzione positiva o negativa dell’asse x

Dobbiamo dimostrare che la concavità di una parabola con asse di simmetria orizzontale è diretta verso la direzione positiva dell’asse delle {x} se e solo se {a>0}, mentre è diretta verso la direzione negativa dell’asse delle {x} se e solo se {a < 0}. Ricordiamo che {a} è il coefficiente del termine di secondo grado nell’equazione della parabola.

Dalla definizione di parabola come luogo geometrico, abbiamo che:

• se una parabola con asse di simmetria orizzontale rivolge la propria concavità verso la direzione positiva dell’asse delle {x}, allora abbiamo che il fuoco si trova a destra della direttrice, ovvero {x_F > d};
• se una parabola con asse di simmetria orizzontale rivolge invece la propria concavità verso la direzione negativa dell’asse delle {x}, allora abbiamo che il fuoco si trova a sinistra delle direttrice, ovvero {x_F < d}.

Così dobbiamo in pratica dimostrare la validità delle seguenti equivalenze logiche:

a > 0 \iff \underbrace{x_F > d}_{\substack{\text{concavità rivolta } \\  \text{verso la direzione } \\ \text{positiva dell'asse x}}}

e:

a<0 \iff \underbrace{x_F < d}_{\substack{\text{concavità rivolta } \\  \text{verso la direzione } \\ \text{negativa dell'asse x}}}

Osservazione. Ricordiamo che in generale due proposizioni {A} e {B} sono logicamente equivalenti, e si scrive {A \iff B}, se valgono entrambe le implicazioni logiche {A \: \Rightarrow \: B} e {B \: \Rightarrow \: A}.

Il metodo che stiamo seguendo è del tutto simile a quello già visto per il caso della parabola con asse di simmetria verticale.

Partiamo dalla prima equivalenza logica. Per dimostrarla, si tratta di dimostrare le seguenti implicazioni:

a> 0 \quad \Rightarrow \quad x_F > d

e:

x_F> d \quad \Rightarrow a>0

Per la prima implicazione, basta osservare che si ha {a=\dfrac{1}{2(x_F-d)}}. Di conseguenza:

x_F > d \quad \Rightarrow \quad \dfrac{1}{2(x_F-d)} > 0 \quad \Rightarrow \quad x_F-d > 0 \quad \Rightarrow \: x_F > d

e quindi la prima implicazione risulta dimostrata.

Per la seconda implicazione, basta ricordare che {x_F=\dfrac{1-\Delta}{4a}} e che {d=-\dfrac{1+\Delta}{4a}}. Di conseguenza:

x_F>d \quad \Rightarrow \quad \dfrac{1-\Delta}{4a}> -\dfrac{1+\Delta}{4a} \quad \Rightarrow\dfrac{2}{4a} > 0 \quad \Rightarrow \: a > 0

Quindi anche la seconda implicazione risulta dimostrata. Di conseguenza abbiamo dimostrato che la concavità di una parabola con asse orizzontale è rivolta verso la direzione positiva dell’asse delle {x} se e solo se {a > 0}.

In modo del tutto simile, si può dimostrare anche l’equivalenza logica:

a<0 \iff x_F < d

Infatti, basta dimostrare le due implicazioni:

a <0 \quad \Rightarrow \quad x_F < d

e:

x_F< d \quad \Rightarrow \quad a < 0

Procedendo con le stesse sostituzioni utilizzate in precedenza abbiamo rispettivamente:

a < 0 \quad \Rightarrow \quad \dfrac{1}{2(x_F-d)}< 0 \quad \Rightarrow \quad x_F-d<0 \quad \Rightarrow \quad x_F < d

e:

x_F < d \quad \Rightarrow \quad \dfrac{1-\Delta}{4a}<- \dfrac{1+\Delta}{4a} \quad \Rightarrow \quad \dfrac{2}{4a}< 0 \quad \Rightarrow \quad a <0

Entrambe le implicazioni risultano pertanto dimostrate e si perviene così al risultato che la concavità di una parabola con asse orizzontale è rivolta verso la direzione negativa dell’asse delle {x} se e solo se {a < 0}.

Conclusioni

Questa lezione relativa alla parabola con asse di simmetria orizzontale si conclude qui. Per chi desidera uno studio parallelo dei due casi di parabole con asse verticale ed orizzontale, rimandiamo alla lezione introduttiva sulla parabola.

Nella prossima lezione ci occuperemo del caso di parabole con vertice nell’origine e del caso di parabole comunque passanti per l’origine. Presteremo così attenzione alla forma che assume l’equazione della parabola nel caso in cui il suo vertice appartenga all’origine o comunque se esiste un punto della parabola che corrisponde all’origine degli assi. Ed analizzeremo tali situazioni sia nel caso di parabole con asse verticale, sia nel caso di parabole con asse orizzontale. Infine, ci occuperemo anche delle situazioni nelle quali una parabola ha il vertice appartenente ad uno degli assi coordinati.

Come sempre, un saluto a tutti voi e buono studio con SìMatematica!