Intersezioni di una parabola con una retta

 - 

Parabola (scuole superiori)

Le eventuali intersezioni di una parabola con una retta si ottengono mettendo a sistema l’equazione della parabola e l’equazione della retta. In tal modo si ottiene per sostituzione un’equazione risolvente, il cui determinante fornisce informazioni sulle posizioni della retta rispetto alla parabola.

In particolare, le intersezioni di una parabola con una retta possono dare due punti di intersezione nel caso in cui la retta sia secante e non parallela all’asse della parabola, un punto di intersezione nel caso in cui la retta sia secante e parallela all’asse di simmetria della parabola, ancora un punto di intersezione qualora la retta sia tangente alla parabola, ed infine nessun punto di intersezione se la retta è esterna alla parabola.

Rispetto a quanto visto nel caso della circonferenza, può stupire il fatto che una retta secante possa avere anche un unico punto di intersezione con la parabola. Ciò riguarda il solo caso di una retta verticale od orizzontale, tale da essere parallela all’asse della parabola, ed è conseguenza del fatto che la parabola è una curva aperta. Nella circonferenza, che è invece una curva chiusa, le intersezioni con una retta secante devono invece sempre risultare necessariamente in due punti di intersezione.

Nel caso in cui la retta sia non parallela agli assi coordinati, si hanno soltanto tre casi del tutto simili a quelli visti nel caso della circonferenza: determinante maggiore di zero (retta secante con due punti di intersezione), determinante nullo (retta tangente con un punto di intersezione), e infine determinante minore di zero (retta esterna alla circonferenza, quindi nessun punto di intersezione). Ai vari casi corrispondono, evidentemente, delle possibili posizioni della retta rispetto alla parabola.

Ma vediamo subito nel dettaglio come determinare le eventuali intersezioni di una parabola con una retta, studiando quindi le possibili posizioni di una retta rispetto ad una parabola, anche con esempi.

Possibili posizioni di una retta rispetto ad una parabola (intersezioni di una parabola con una retta)

Consideriamo una retta non parallela agli assi coordinati, con equazione ad esempio in forma implicita:

r:a_1x+b_1y+c_1=0, \qquad a_1\neq 0 \: \wedge\:  b_1 \neq 0, \quad a_1,b_1,c_1 \in \R

La condizione di non parallelismo della retta rispetto agli assi coordinati si esprime richiedendo che entrambi i coefficienti {a_1} e {b_1} siano diversi da zero. In questo modo, la retta {r} non sarà mai orizzontale o verticale.

In modo del tutto simile a quanto visto per la circonferenza, gli eventuali punti di intersezione tra una parabola ed una retta si determinano mettendo a sistema l’equazione della parabola e l’equazione della retta. Così ad esempio, se abbiamo una parabola con asse verticale di equazione:

\mathscr{P}: y=ax^2+bx+c, \qquad a \neq 0, \quad a,b,c \in \R

le eventuali intersezioni della parabola {\mathscr{P}} e della retta {r} si ricercano risolvendo il sistema:

\begin{cases} \mathscr{P}:y=ax^2+bx+c \\ \\  r:a_1x+b_1y+c_1=0\end{cases}

Per risolvere il sistema, l’idea è quella di riscrivere anzitutto l’equazione della retta in forma esplicita:

\begin{cases} \mathscr{P}:y=ax^2+bx+c \\ \\  r:y=mx+q\end{cases}

e quindi sostituire l’espressione {mx+q}, corrispondente alla {y}, nella prima equazione:

\begin{cases} mx+q=ax^2+bx+c \\ \\ y=mx+q\end{cases}

Concentrandoci a questo punto soltanto sulla prima equazione, ciò che otteniamo è un’equazione di secondo grado nella sola variabile {x}:

\begin{align*} & ax^2+bx+c-mx-q=0; \\ \\ & ax^2+bx-mx+c-q=0;\\ \\ & ax^2+(b-m)x+c-q=0 \end{align*}

Come possiamo vedere, abbiamo portato tutti i termini al primo membro, e dopo averli riordinati abbiamo eseguito un raccoglimento parziale per {x}.

E’ abbastanza immediato accorgersi che l’equazione ottenuta è un’equazione di secondo grado in forma normale. Infatti, ponendo {A=a, B=b-m} e {C=c-q} la precedente equazione diviene:

Ax^2+Bx+C=0

Abbiamo così scritto l’equazione risolvente del sistema.

Ora, dalla teoria sulle equazioni di secondo grado sappiamo che le soluzioni dell’equazione dipendono dal determinante o discriminante {\Delta}, ovvero dalla quantità {B^2-4AC}. Inoltre, le eventuali soluzioni reali dell’equazione rappresentano le ascisse dei punti di intersezione fra la parabola e la retta date.

Così, distinguiamo i seguenti casi:

• {\Delta > 0 }: l’equazione ammette due soluzioni reali e distinte e fornisce due ascisse per i punti di intersezione tra la parabola e la retta. Le corrispondenti ordinate si ottengono poi sostituendo i valori delle ascisse nella seconda equazione a sistema. Abbiamo così due punti di intersezione e la retta data è secante alla parabola;
• {\Delta = 0}: l’equazione ammette due soluzioni reali e coincidenti, fornendo così un solo punto di intersezione tra la parabola e la retta, la quale risulta tangente alla parabola nel punto ottenuto;
• infine, {\Delta < 0}: l’equazione non ammette alcuna soluzione reale, e di conseguenza non esistono punti di intersezione tra la retta e la parabola. In questo caso la retta risulta esterna alla parabola.

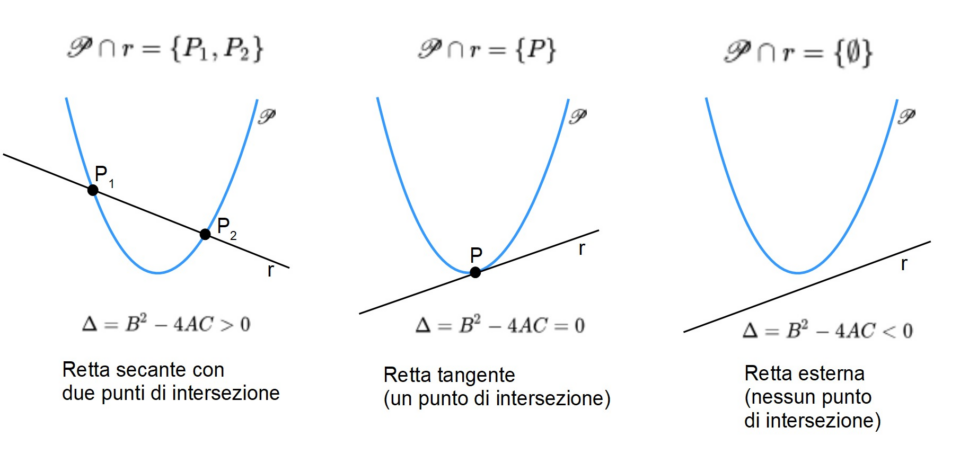
Osserviamo che con la simbologia {\mathscr{P} \cap r} intendiamo rappresentare l’operazione di intersezione tra la parabola e la retta, utilizzando il linguaggio degli insiemi. Ciò ha senso poiché una retta e una parabola sono entrambe dei luoghi di punti, e quindi degli “insiemi” di punti.

Ora, considerando sempre una parabola con asse di simmetria verticale, nel caso in cui la retta sia parallela agli assi coordinati esistono due casi.

Se la retta è orizzontale, questa avrà equazione della forma:

r:y=h, \quad h \in \R

Il sistema da impostare per la ricerca degli eventuali punti di intersezione sarà:

\begin{cases} \mathscr{P}:  y=ax^2+bx+c \\ \\ r: y=h\end{cases}

da cui risulterà l’equazione risolvente:

ax^2+bx+c-h=0

Il determinante dell’equazione potrà essere maggiore di zero, uguale a zero o minore di zero, ottenendo rispettivamente due punti di intersezione (retta secante), un punto di intersezione (retta tangente) oppure nessun punto di intersezione (retta esterna). Non abbiamo quindi in questa circostanza differenza alcuna rispetto al caso generale.

Particolare è invece il caso in cui la parabola sia con asse di simmetria verticale e anche la retta {r} sia verticale (retta parallela all’asse di simmetria della parabola). In tal caso, la retta ha equazione della forma:

r:x=h, \qquad h \in \R

ed il sistema da impostare è:

\begin{cases} \mathscr{P}:  y=ax^2+bx+c \\ \\ r:x=h\end{cases}

Dal sistema si ottiene per sostituzione l’equazione risolvente:

y=\underbrace{ah^2+bh+c}_{\text{numero reale}}

L’equazione fornisce banalmente l’ordinata dell’unico punto di intersezione tra la parabola e la retta. Così per ogni possibile valore di {h} otteniamo sempre un unico valore dell’ordinata (l’espressione al secondo membro dell’uguaglianza appena scritta ha senso in tutti i reali). Di conseguenza, tra una parabola con asse verticale e una retta verticale esiste sempre un punto di intersezione ed è unico. Inoltre, la retta risulta secante alla parabola.

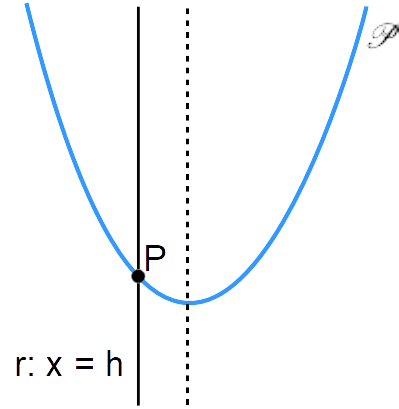
E’ qui utile osservare che l’ordinata del punto di intersezione si può ottenere semplicemente sostituendo il valore {h} dell’ascissa nell’equazione della parabola. Così il punto di intersezione {P} ha coordinate {P=(h, ah^2+bh+c)}.

Osserviamo inoltre che in questo caso abbiamo un solo punto di intersezione, pur a fronte di una retta secante, poiché la parabola è una curva piana aperta.

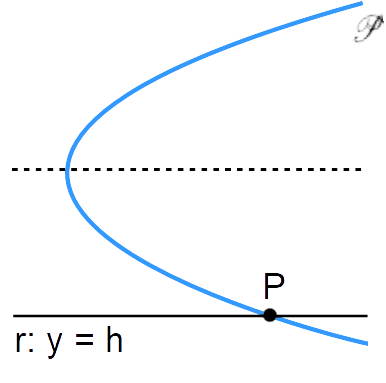
Allo stesso modo, per una parabola con asse di simmetria orizzontale, e quindi avente equazione {x=ay^2+by+c} possiamo concludere che:

• l’intersezione con una retta non parallela agli assi coordinati oppure verticale {r:x=h} potrà fornire due punti di intersezione (retta secante), un punto di intersezione (retta tangente) o nessun punto di intersezione (retta esterna), in base al determinante dell’equazione risolvente. Ciò rientra nel caso più generale;
• l’intersezione con una retta orizzontale {r: y=h}, e quindi con una retta parallela all’asse di simmetria, fornirà sempre un unico punto di intersezione {P} con la parabola. E tale punto avrà coordinate {P=(ah^2+bh+c, h)}. La retta inoltre risulterà sempre secante alla parabola stessa (vedi figura a seguire).

Esempi

Vediamo ora degli esempi sulle intersezioni di una parabola con una retta, in modo da stabilire le posizioni della retta rispetto alla parabola nei vari casi, determinando gli eventuali punti di intersezione.

Esempio 1

Determinare gli eventuali punti di intersezione tra la parabola {\mathscr{P}:y=3x^2+x+1} e la retta {r: 2x-y+1=0}

Per la ricerca degli eventuali punti di intersezione tra la parabola e la retta date, dobbiamo mettere a sistema le rispettive equazioni. I punti le cui corrispondenti coppie di coordinate sono soluzioni del sistema, se esistono, saranno i punti di intersezione cercati.

\begin{cases} \mathscr{P}: y=3x^2+x+1 \\ \\ r:2x-y+1=0\end{cases}

Il primo passo per risolvere il sistema consiste nel ricondurre l’equazione della retta, che è data in forma implicita, alla forma esplicita:

\begin{cases} \mathscr{P}: y=3x^2+x+1 \\ \\ r:y=2x+1\end{cases}

Ora, la seconda equazione fornisce un’espressione per {y} in funzione della variabile {x}. L’idea è così quella di sostituire alla {y} nella prima equazione l’espressione {2x+1}. In tal modo, la prima equazione a sistema risulterà nella sola incognita {x}:

\begin{cases} 2x+1=3x^2+x+1 \\ \\ r:y=2x+1\end{cases}

A questo punto consideriamo separatamente la prima equazione, che è l’equazione risolvente del sistema, e risolviamola rispetto ad {x}:

\begin{align*} &3x^2-2x+x+\cancel{1}-\cancel{1}=0; \\ \\ & 3x^2-x=0;\\ \\ & x(3x-1)=0 \quad \Rightarrow \quad x=0 \quad \vee \quad x =\dfrac{1}{3}\end{align*}

Ricordiamo che abbiamo risolto l’equazione di secondo grado ottenuta tenendo conto che questa è spuria.

Ora, il nostro obiettivo è ricavare per ogni valore della {x} il corrispondente valore della {y}. Per fare questo, sostituiamo ciascuno dei valori ottenuti per la {x} nella seconda equazione a sistema. Abbiamo così, rispettivamente:

y=2x+1 \quad \text{con} \quad x = \textbf{0} \quad \Rightarrow \quad y=\textbf{1}

e:

\small y=2x+1 \quad \text{con} \quad x=\boldsymbol{\dfrac{1}{3}} \quad \Rightarrow \quad y=2 \cdot\dfrac{1}{3}+1 \quad \Rightarrow \: y=\boldsymbol{\dfrac{5}{3}}

Ciascuna delle coppie {(x,y)} così ottenuta è soluzione del sistema, e possiamo scrivere in corrispondenza di ognuna di esse i punti di intersezione:

P_1=(0,1); \qquad P_2=\left( \dfrac{1}{3}, \dfrac{5}{3}\right)

Questi sono i punti di intersezione tra la retta e la parabola date. Quindi la retta {r} è secante alla parabola, nei due punti {P_1} e {P_2}.

Abbiamo quindi visto in questo primo esercizio come determinare nella pratica la posizione di una retta rispetto ad una parabola tra le varie possibili posizioni.

Esempio 2

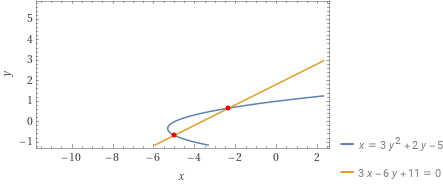
Determinare gli eventuali punti di intersezione tra la parabola {\mathscr{P}:x=3y^2+2y-5} e la retta {r: 3x-6y+11=0}.

E’ prima di tutto importante notare che in questo caso la parabola ha asse di simmetria orizzontale, ovvero parallelo all’asse delle {x}. Infatti, l’equazione della parabola è della forma {x=f(y)}.

Di conseguenza, per risolvere il sistema conviene in questo caso esplicitare dalla seconda equazione la variabile {x}, e non più la variabile {y} come nell’esercizio precedente. In tal modo, potremo comodamente effettuare l’opportuna sostituzione soltanto nella {y} al primo membro dell’equazione della parabola.

Quindi, mettiamo le equazioni della parabola e della retta a sistema:

\begin{cases} \mathscr{P}:x=3y^2+2y-5 \\ \\ r: 3x-6y+11=0  \end{cases}

e procediamo esplicitando la variabile {x} nell’equazione della retta:

\begin{cases} \mathscr{P}:x=3y^2+2y-5 \\ \\ r: x=2y-\dfrac{11}{3} \end{cases}

A questo punto sostituiamo l’espressione così ottenuta per la {x}, ovvero l’espressione {2y-\dfrac{11}{3}} nella prima equazione a sistema, che consideriamo separatamente. In questo modo, otteniamo l’equazione risolvente del sistema:

\begin{align*} &\cancel{2y}-\dfrac{11}{3}= 3y^2+\cancel{2y}-5; \\ \\ & 3y^2=-\dfrac{11}{3}+5; \\ \\ & 3y^2=\dfrac{-11+15}{3};\\ \\ & y^2=\dfrac{4}{9} \quad \Rightarrow \quad y_{1,2}=\pm \sqrt {\dfrac{4}{9}}=\pm \dfrac{2}{3}\end{align*}

Ora calcoliamo i valori dell’ascissa corrispondenti a ciascuna ordinata. Per fare ciò, basta sostituire i valori di {y} appena determinati nella seconda equazione a sistema. Cominciamo dal primo valore:

\begin{align*} & x=2y-\dfrac{11}{3} \quad \text{con} \quad y= \boldsymbol{\dfrac{2}{3}} \\ \\ & \Rightarrow \quad x = 2 \cdot \dfrac{2}{3}-\dfrac{11}{3}=\dfrac{4}{3}-\dfrac{11}{3}=\boldsymbol{-\dfrac{7}{3} }\end{align*}

Infine, per il secondo valore della {y}:

\begin{align*} & x=2y-\dfrac{11}{3} \quad \text{con} \quad y= \boldsymbol{-\dfrac{2}{3}} \\ \\ & \Rightarrow \quad x = 2 \cdot \left( -\dfrac{2}{3}\right)-\dfrac{11}{3}=-\dfrac{4}{3}-\dfrac{11}{3}=-\dfrac{15}{3}=\boldsymbol{-5} \end{align*}

Abbiamo così tra la parabola e la retta date i due punti di intersezione:

P_1=\left( -\dfrac{7}{3}, \dfrac{2}{3}\right); \qquad P_2=\left( -5, -\dfrac{2}{3}\right)

e la retta {r} risulta secante alla parabola.

Esempio 3

Determinare gli eventuali punti di intersezione tra la parabola {\mathscr{P}:y=x^2+3x+6} e la retta {r:x=-1}.

La parabola in esame ha equazione della forma {y=ax^2+bx+c}, ed è quindi ad asse di simmetria verticale. Inoltre, la retta {r} è una retta verticale. Infatti, tutti i suoi punti hanno la stessa ascissa, uguale a {-1}. Di conseguenza, dato che la la retta {r} è parallela all’asse di simmetria della parabola, la retta {r} dovrà essere necessariamente secante alla parabola con un solo punto di intersezione.

Il sistema da impostare è il seguente:

\begin{cases} \mathscr{P}:y=x^2+3x+6 \\ \\ r:x=\boldsymbol{-1}\end{cases}

Per risolvere il sistema basta sostituire il valore di {x} fornito dalla seconda equazione nella prima equazione, che consideriamo separatamente:

\begin{align*} &y=(-1)^2+3\cdot(-1) + 6 \quad \Rightarrow \quad y=1-3+6 \quad \Rightarrow \: y=\boldsymbol{4}\end{align*}

Otteniamo così l’unico punto di intersezione:

P=(-1, 4)

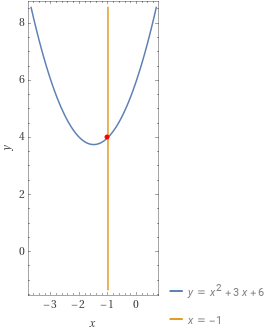
Come possiamo anche vedere dalla figura la retta {r} è secante alla parabola, pur avendosi un unico punto di intersezione. Lo sottolineiamo ancora: ciò è dovuto al fatto che la parabola è una curva aperta e quindi, diversamente dalla circonferenza, possiamo avere una retta secante alla parabola anche a fronte di un unico punto di intersezione, come in questo caso. Questo avviene, come in questo esercizio, nella particolare circostanza ove la retta {r} e l’asse di simmetria della parabola sono paralleli tra loro.

Esempio 4

Determinare gli eventuali punti di intersezione tra la parabola {\mathscr{P}: y=2x^2+x-3} e la retta {r} di equazione {y=\dfrac{1}{3}x-\dfrac{55}{18}}.

Cominciamo mettendo a sistema l’equazione della parabola e l’equazione della retta:

\begin{cases}\mathscr{P}: y=2x^2+x-3 \\ \\r:y=\dfrac{1}{3}x-\dfrac{55}{18}  \end{cases}

L’equazione della retta è già in forma esplicita, per cui possiamo direttamente sostituire l’espressione di {y} fornita dalla seconda equazione nella prima equazione a sistema. Consideriamo l’equazione che così si ottiene separatamente:

\begin{align*} &\dfrac{1}{3}x-\dfrac{55}{18}=2x^2+x-3;\\ \\ & 2x^2+\left( 1-\dfrac{1}{3}\right)x-3+\dfrac{55}{18}=0;\\ \\ & 2x^2+\dfrac{2}{3}x+\dfrac{1}{18}=0\end{align*}

Ora l’equazione è nella sola incognita {x}. Si tratta in particolare di un’equazione di secondo grado che possiamo risolvere che la formula del {\Delta} (formula risolutiva):

\begin{align*} & x_{1,2}=\dfrac{-\dfrac{2}{3}\pm \sqrt{\dfrac{4}{9}-4 \cdot 2 \cdot \dfrac{1}{18}}}{2 \cdot 2}=\dfrac{-\dfrac{2}{3}\pm \sqrt{\dfrac{4}{9}-\dfrac{4}{9}}}{4}=\\ \\ & =-\dfrac{2}{3}\cdot\dfrac{1}{4}=\boldsymbol{-\dfrac{1}{6}} \end{align*}

Otteniamo in questo caso un’unica ascissa. La corrispondente ordinata si calcola sostituendo il valore dell’ascissa appena ottenuto nella seconda equazione a sistema:

\begin{align*} &y=\dfrac{1}{3}x-\dfrac{55}{18} \quad \text{con} \quad x=-\dfrac{1}{6}\\ \\ & \Rightarrow \quad y=\dfrac{1}{3} \cdot \left( -\dfrac{1}{6}\right)-\dfrac{55}{18}=-\dfrac{56}{18}=\boldsymbol{-\dfrac{28}{9}}\end{align*}

Così la parabola e la retta in esame presentano un unico punto di intersezione:

P=\left( -\dfrac{1}{6}, -\dfrac{28}{9}\right)

Ora, osserviamo che la retta {r} non è parallela agli assi coordinati. Infatti, non è sicuramente una retta verticale poiché è della forma {y=f(x)} (una retta verticale è invece della forma {x=h, \: h \in \R}). Inoltre, non è nemmeno una retta orizzontale poiché il suo coefficiente angolare è diverso dal zero. Quindi, pur avendo un unico punto di intersezione non siamo nel caso di retta parallela all’asse della parabola. Di conseguenza, la retta non è secante alla parabola, ma bensì tangente.

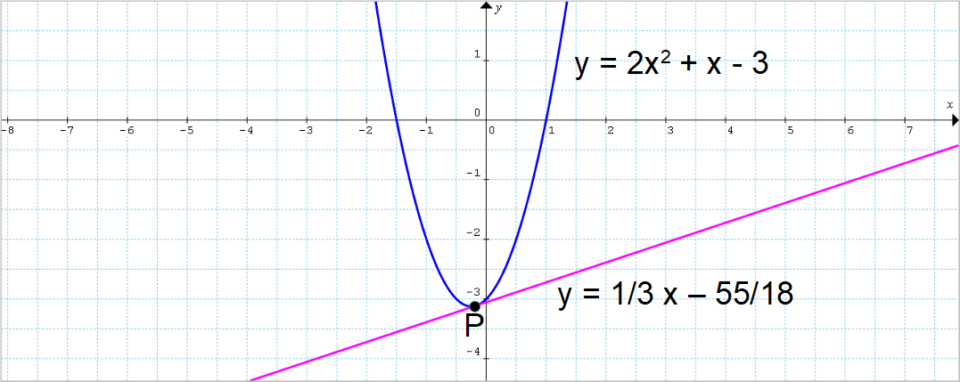
Veniamo ora all’ultimo di questa serie di esempi sulle intersezioni di una parabola con una retta. In particolare, ci occuperemo di un caso nel quale non esiste alcun punto di intersezione tra la retta e la parabola. Ci ritroveremo così, tra le possibili posizioni della retta rispetto alla parabola, nel caso in cui la retta è esterna alla parabola.

Esempio 5

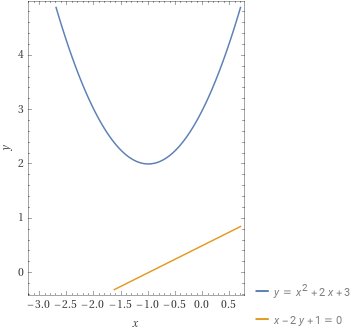
Determinare gli eventuali punti di intersezione tra la parabola {\mathscr{P}: y=x^2+2x+3} e la retta {r:x-2y+1=0}.

Come al solito, impostiamo il sistema:

\begin{cases}y=x^2+2x+3 \\ \\  r:x-2y+1=0\end{cases}

Riscriviamo l’equazione della retta nella forma esplicita:

\begin{cases}y=x^2+2x+3 \\ \\  r:y=\dfrac{1}{2}x+\dfrac{1}{2}\end{cases}

Ora sostituiamo l’espressione appena ottenuta per {y} nella prima equazione, che scriviamo separatamente:

\begin{align*} &\dfrac{1}{2}x+\dfrac{1}{2}=x^2+2x+3; \\ \\ & x^2+\left( 2-\dfrac{1}{2}\right)x+3-\dfrac{1}{2}=0;\\ \\ & x^2+\dfrac{3}{2}x+\dfrac{5}{2}=0\end{align*}

Per comodità riconduciamo l’equazione di secondo grado appena scritta alla forma intera:

2x^2+3x+5=0

A questo punto proviamo a risolvere l’equazione:

x_{1,2}=\dfrac{-3 \pm \sqrt{3^2-4 \cdot 2 \cdot 5}}{2 \cdot 2}= \dots

Non è possibile risolvere l’equazione nei reali poiché la quantità {\Delta = B^2-4AC} relativa all’equazione risolvente è minore di zero:

\Delta=B^2-4AC=3^2-4 \cdot 2 \cdot 5=9-40 < 0

Così in conclusione la parabola e la retta date non hanno nessun punto di intersezione. In particolare, la retta {r} risulta esterna alla parabola.

Conclusioni – Possibili posizioni di una retta rispetto ad una parabola

A conclusione della lezione sulle intersezioni di una parabola con una retta riteniamo utile riassumere i vari casi che si possono presentare.

Se la retta non è né orizzontale né verticale, a prescindere che la parabola abbia asse di simmetria orizzontale o verticale, una volta impostato il sistema contenente le rispettive equazioni della parabola e della retta possiamo cadere in uno dei tre seguenti casi:

• determinante dell’equazione risolvente maggiore di zero: la parabola e la retta hanno due punti di intersezione e la retta risulta secante alla parabola;
• determinante dell’equazione risolvente uguale a zero: la parabola e la retta hanno un unico punto di intersezione e la retta, non essendo né orizzontale né verticale, è tangente alla parabola;
• infine, determinante dell’equazione risolvente minore di zero: la parabola e la retta non hanno alcun punto in comune. Non esistono dunque punti di intersezione tra la parabola e la retta, e quest’ultima risulta esterna alla parabola.

Nel caso in cui invece la retta data risulti orizzontale o verticale, e la parabola sia indifferentemente ad asse orizzontale o verticale:

• se la retta non è parallela all’asse della parabola, allora si ricade in uno dei tre casi precedenti;
• se la retta è invece parallela all’asse della parabola, allora abbiamo un unico punto di intersezione. Inoltre la retta risulta secante alla parabola.

Ora per questa lezione è davvero tutto. Un saluto e, come sempre, buono studio con SìMatematica!