Nell’equazione di una retta del piano cartesiano in forma esplicita compare un’espressione per la variabile dipendente y scritta in funzione della variabile indipendente x. Tale espressione è data da un polinomio di primo grado a coefficienti reali m e q. Il coefficiente m del termine in x è detto coefficiente angolare, mentre il termine noto q è detto ordinata all’origine. In particolare, l’equazione di una retta in forma esplicita si scrive y = mx + q.
Dopo aver visto le equazioni relative ad una retta del piano cartesiano passante per l’origine, in questa lezione ci occuperemo dell’equazione di una generica retta del piano in forma esplicita, data da un’uguaglianza ove al primo membro abbiamo la variabile dipendente {y} e al secondo membro abbiamo un polinomio di primo grado nella variabile indipendente {x}.
Nel corso della lezione mostreremo come una tale equazione rappresenta una qualsiasi retta del piano cartesiano, con la sola eccezione di rette parallele all’asse {y} (compreso lo stesso asse {y}). Il problema dell’equazione di una retta nella forma esplicita è dunque quello di non poter rappresentare rette del tipo {x=k}, con {k} numero reale.
Vediamo allora subito l’equazione di una retta del piano in forma esplicita, con relativi esempi.
Come si scrive l’equazione di una retta del piano in forma esplicita
L’equazione in forma esplicita di una retta nel piano cartesiano si scrive come:{y= mx + q, \qquad m, q \in \R} ove {m} è il coefficiente angolare mentre {q} è l’ordinata all’origine.
Così, una volta noti {m} e {q} una retta risulta univocamente determinata. In altre parole, ad ogni coppia di valori {m} e {q} corrisponde una ed una sola retta del piano cartesiano.
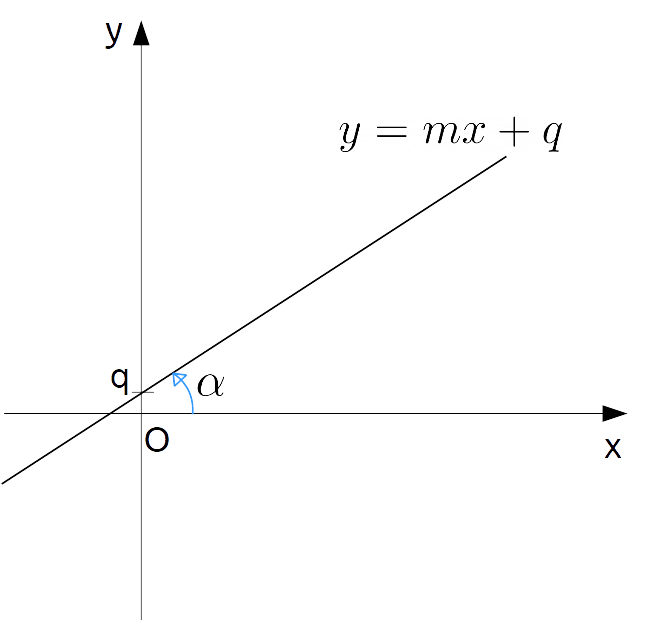
Dal coefficiente angolare {m} dipende la pendenza della retta rispetto alla direzione positiva dell’asse delle {x}. Più precisamente, l’angolo {\alpha} che la retta forma con la direzione positiva dell’asse delle {x} dipende dal coefficiente angolare {m} secondo la relazione:
\alpha = \arctg m
valida esclusivamente nel caso di retta non verticale, ovvero di retta non parallela all’asse delle {y}.
Nota: la funzione arcotangente è, sotto opportune ipotesi, l’inversa della funzione tangente. E la tangente di un angolo si definisce come il rapporto tra il seno e il coseno dell’angolo stesso. Infine, il seno e il coseno di un angolo rappresentano rispettivamente l’ordinata e l’ascissa del punto {P} individuato dall’angolo {\alpha} sulla circonferenza goniometrica, ovvero su di una particolare circonferenza di raggio unitario avente per centro l’origine degli assi.
Precisiamo comunque che le funzioni trigonometriche (seno, coseno, ecc.) vengono solitamente introdotte dopo lo studio della retta, per cui chi non conosce ancora tali funzioni può tranquillamente ignorare questa nota, e limitarsi a considerare la funzione arcotangente come una funzione ottenibile mediante la calcolatrice.
Ci occuperemo nel dettaglio della definizione di coefficiente angolare nella prossima lezione.
Ora, l’ordinata all’origine rappresenta il valore assunto dalla variabile dipendente {y} quando la variabile indipendente {x} vale zero. Infatti, se {x=0} abbiamo:
y=mx+q, \quad x=0 \quad \Rightarrow \quad y=q
Da ciò discende che la retta {y=mx+q} passa necessariamente per il punto {P=(0,q)}, ovvero il punto di ascissa {0} ed ordinata {q}.
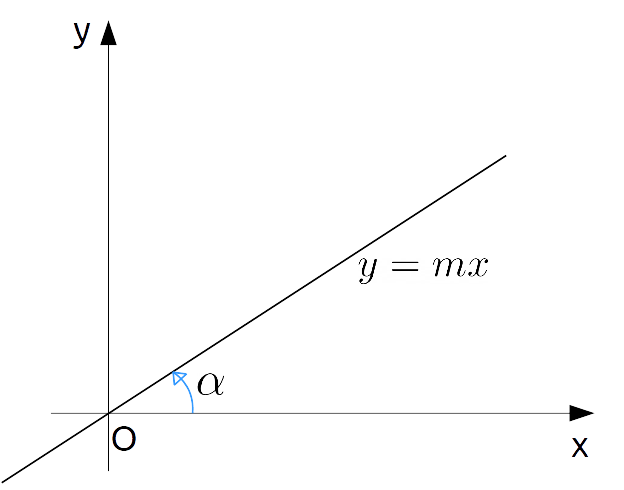
Se {q=0} abbiamo invece:
y=mx+q, \quad q=0 \qquad \Rightarrow \quad y=mx
e ritroviamo il caso di una retta del piano passante per l’origine, come visto nella precedente lezione.
Esempi sull’equazione di una retta in forma esplicita
Esempio 1
L’equazione:
y=2x+5
è della forma {y=mx+q} con coefficiente angolare {m=2} ed ordinata all’origine {q=5}. In particolare, tale equazione rappresenta una retta che non passa per l’origine degli assi. Infatti, l’ordinata all’origine {q} è diversa da zero.
Poiché {q=5}, la retta passa necessariamente per il punto {P=(0,5)}. Infatti, ponendo {x=0} otteniamo:
y=2x+5 \quad \text{con} \quad x=0 \quad \Rightarrow \quad y=2 \cdot 0 + 5 \quad \Rightarrow \quad y= 5Così intanto abbiamo le coordinate di un punto {P} appartenente alla retta.
Ora, in generale per rappresentare graficamente una retta nel piano cartesiano occorre conoscere due punti appartenenti alla retta stessa. Ma per il momento, conosciamo le coordinate del solo punto {P}.
Tuttavia, per determinare le coordinate di un altro punto appartenente alla retta, basta attribuire alla {x} un valore a piacere (ovviamente diverso da {x=0}), e ricavare il corrispondente valore della {y} tramite l’equazione della retta. Ad esempio, ponendo {x=1} abbiamo:
\small y=2x+5 \quad \text{con} \quad x=1 \quad \Rightarrow \quad y=2 \cdot 1 + 5 \quad \Rightarrow \quad y=7Così anche il punto {P_1=(1,7)} appartiene alla retta in esame.
Ma adesso disponiamo di due punti appartenenti alla retta:
P=(0,5), \quad P_1 = (1,7)
Possiamo quindi rappresentare i due punti nel piano cartesiano, e quindi tracciare la retta che passa per i due punti stessi:
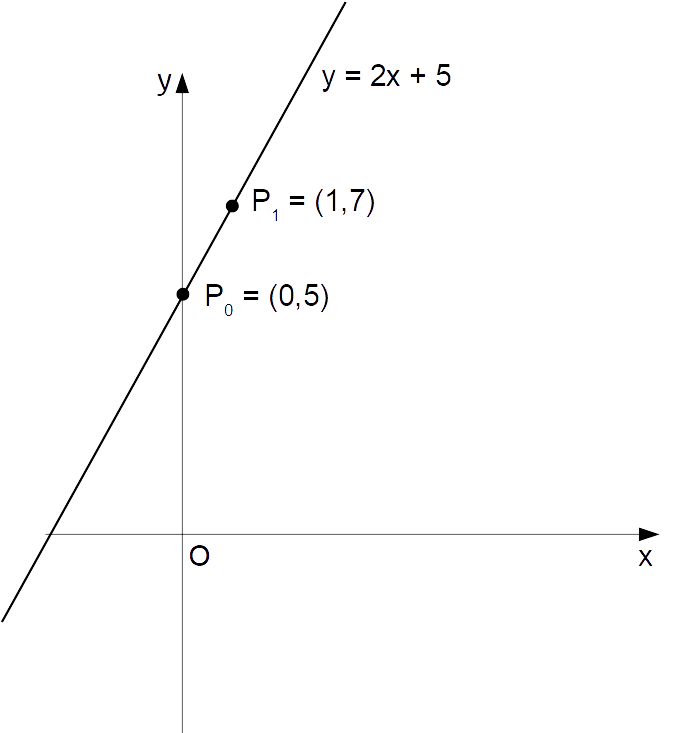
La retta appena disegnata corrisponde proprio alla retta cercata, ovvero la retta di equazione {y=2x+5}.
Esempio 2
La retta di equazione:
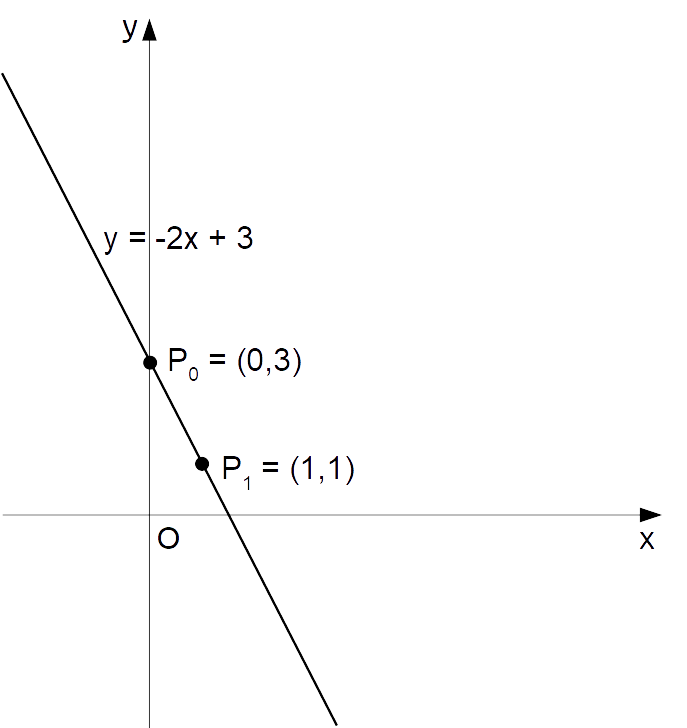
y=-2x+3
ha coefficiente angolare {m=-2} ed ordinata all’origine {q=3}. Procedendo allo stesso modo dell’esempio precedente, possiamo affermare che i due punti seguenti appartengono alla retta in esame:
P=(0,3), \quad P_1=(1, 1)
Di conseguenza, rappresentando i due punti nel piano cartesiano e tracciando la retta che passa per entrambi otteniamo la seguente rappresentazione grafica:
Importante. La tecnica utilizzata negli esempi per disegnare una retta nel piano cartesiano si basa sul fatto che una retta è univocamente individuata una volta noti due punti ad essa appartenenti.
Osservazione. Nella retta dell’esempio 1 il coefficiente angolare è positivo. Ne risulta che, considerando punti appartenenti alla retta, al crescere del valore dell’ascissa cresce anche il valore dell’ordinata. Diversamente, la retta dell’esempio 2 ha un coefficiente angolare negativo, e al crescere del valore dell’ascissa diminuisce il valore dell’ordinata.
Approfondiremo questo aspetto nella prossima lezione dedicata al coefficiente angolare di una retta nel piano.
Equazione di una retta verticale
Osserviamo che l’equazione {y=mx+q} rappresenta una generica retta del piano cartesiano (tranne, come vedremo tra un istante, le rette verticali). Infatti, dato che {q} è un numero reale qualsiasi, l’equazione {y=mx+q} può rappresentare indifferentemente rette passanti per l’origine degli assi o per punti tutti diversi dall’origine. Tuttavia, non esiste alcun valore di {m} per cui l’equazione possa ridursi alla forma {x=k, \: k \in \R} (equazione di una retta verticale, ovvero parallela all’asse {y}).
In particolare, l’equazione {x=k} rappresenta il luogo dei punti tutti aventi distanza dall’asse {y} uguale a {k}. E tale luogo di punti corrisponde, appunto, ad una retta verticale, ovvero parallela all’asse {y}.
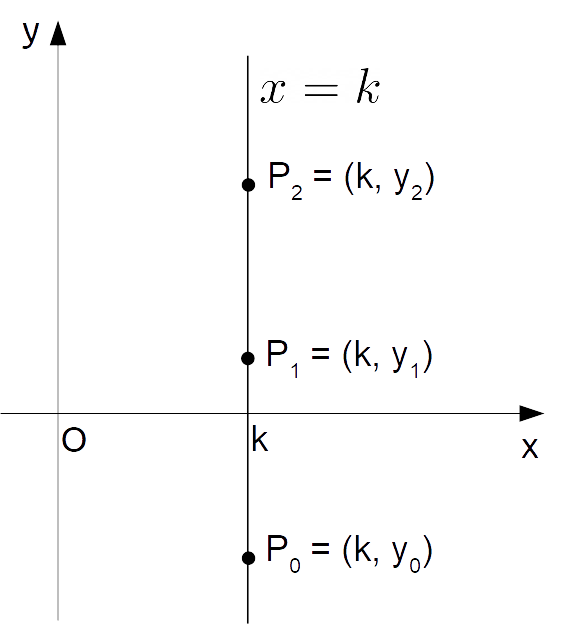
Come evidenzia la figura, tutti i punti appartenenti ad una data retta verticale hanno in comune la stessa ascissa {k}. Infine, il coefficiente angolare di una retta verticale è indefinito. Di conseguenza, l’equazione {y=mx+q} non può rappresentare alcuna retta verticale.
Equazione di una retta orizzontale
Dall’equazione {y=mx+q} è invece possibile ricavare l’equazione di una retta orizzontale ponendo {m=0}:
y=mx+q, \quad m = 0 \quad \Rightarrow \quad y=q
Ci ritroviamo così con un’equazione del tipo {y=k}, ove {k} è una costante reale. Utilizziamo la lettera {k} in questo caso al posto della {q}, poiché effettivamente la nozione di “ordinata all’origine” per una retta orizzontale non è di particolare utilità.
Come mostra la seguente figura, una retta orizzontale è caratterizzata da punti aventi tutti lo stesso valore {k} dell’ordinata.
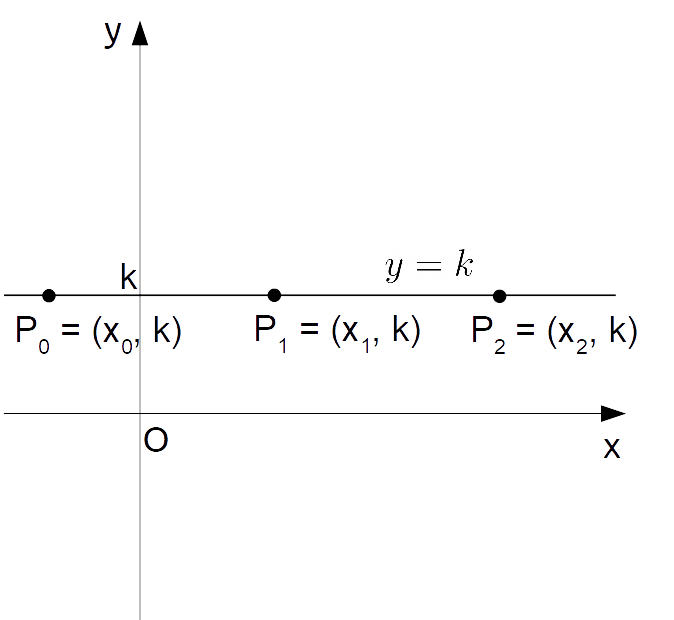
Condizione di appartenenza di un punto P alla retta di equazione y=mx+q
Un punto {P=(x_0, y_0)} appartiene alla retta di equazione {y=mx+q} se e solo se le sue coordinate soddisfano l’equazione stessa, ovvero se e solo se risulta verificata l’uguaglianza:{y_0 = m x_0 + q}
Così per verificare se un punto appartiene ad una data retta, basta sostituire i valori delle sue coordinate nell’equazione della retta stessa. Se l’equazione si riduce ad un’uguaglianza numerica vera, allora il punto appartiene alla retta.
Esempio
Stabilire se i punti {P_1 = (2,5)} e {P_2 = (-3, 4)} appartengono alla retta di equazione {y=\dfrac{2}{3}x+6}.
Cominciamo sostituendo i valori dell’ascissa e dell’ordinata del punto {P_1 = (2,5)} nell’equazione {y=\dfrac{2}{3}x+6}. In altre parole, si tratta di porre {x_0=2} e {y_0=5} nell’equazione corrispondente alla retta in esame. Abbiamo:
\begin{align*} & y=\dfrac{2}{3}x+6 \quad \text{con} \quad x_0=2, \: y_0 = 5 \\ \\ & \Rightarrow \quad y_0=\dfrac{2}{3}x_0+6 \quad \Rightarrow \quad 5=\dfrac{2}{3}\cdot 2 +6 \quad \Rightarrow \quad 5=\dfrac{4}{3}+6 \\ \\ & \Rightarrow \quad 5=\dfrac{4+18}{3} \quad \Rightarrow \quad 5=\dfrac{22}{3}\end{align*}Poiché l’uguaglianza numerica ottenuta è falsa, il punto {P_1 = (2,5)} non appartiene alla retta di equazione {y=\dfrac{2}{3}x+6}.
Veniamo ora al punto {P_2 = (-3, 4)}. Si ha:
\begin{align*} & y=\dfrac{2}{3}x+6 \quad \text{con} \quad x_0=-3, \: y_0 = 4 \\ \\ & \Rightarrow \quad y_0=\dfrac{2}{3}x_0+6 \quad \Rightarrow 4=\dfrac{2}{3} \cdot (-3)+6 \quad \Rightarrow \quad 4=-2+6 \\ \\ & \Rightarrow \quad 4=4\end{align*}Stavolta otteniamo un’uguaglianza numerica vera. Di conseguenza, il punto {P_2 = (-3, 4)} appartiene alla retta di equazione {y=\dfrac{2}{3}x+6}.
Equazione esplicita di una retta noti il coefficiente angolare e le coordinate di un punto della retta
Noti il coefficiente angolare {m} e le coordinate {x_0} ed {y_0} di un punto {P} appartenente alla retta, è possibile scrivere l’equazione della retta stessa come:
y-y_0 = m (x - x_0)
Infatti, se {Q=(x,y)} è un generico punto di coordinate incognite appartenente alla retta, vale necessariamente l’uguaglianza:
y=mx+ q \qquad (1)
Allo stesso modo, per il punto {P=(x_0, y_0)} di coordinate note, vale l’uguaglianza:
y_0 = m x_0 + q \qquad (2)
Ora, fissata una certa quantità {Q} reale, sotto le ipotesi del primo principio di equivalenza è possibile scrivere, in merito alla prima equazione:
y-Q=mx+q-Q
Ma dato che la seconda equazione ci dice che le due quantità {y_0} e {mx_0 + q} sono tra loro uguali, possiamo indifferentemente sostituire a {Q} una di tali quantità. Così ponendo ad esempio al primo membro {Q=y_0} ed al secondo membro {Q=mx_0+q} la precedente diviene:
y-y_0=mx+q-(mx_0+q)
ovvero:
y-y_0=mx+q-mx_0-q
e quindi, raccogliendo al secondo membro per {m} e sommando i termini simili:
y-y_0 = m(x-x_0)
Ritroviamo così l’equazione di una retta note le coordinate di un punto e il coefficiente angolare.
Esempio (equazione di una retta in forma esplicita noti il coefficiente angolare e le coordinate di un suo punto)
Scrivere l’equazione in forma esplicita di una retta avente coefficiente angolare {m=4} note le coordinate del punto {P=(-2,-5)}.
A partire dall’equazione:
y-y_0 = m(x - x_0)
otteniamo, sostituendo i valori forniti nel testo:
y-(-5)=4(x-(-2))
ovvero:
y+5=4(x+2)
Infine, eseguendo la moltiplicazione al secondo membro ed isolando la {y} al primo membro, otteniamo l’equazione:
y=4x+8-5 \quad \Rightarrow \quad y=4x+3
che è l’equazione cercata.
Conclusioni
Per quanto riguarda l’equazione di una retta in forma esplicita è tutto. Ma prima di salutarci, è importante fare un’ultima riflessione che anticipa quanto vedremo nella prossima lezione.
Come visto nei precedenti esempi, una retta è univocamente determinata una volta note le coordinate di due suoi punti. Infatti, una volta rappresentati due punti nel piano cartesiano, è possibile tracciare un’unica retta tale da appartenere ad entrambi i punti.
Ma come evidenziato nella parte finale della lezione, una retta è univocamente individuata anche noti il coefficiente angolare e le coordinate di un solo punto ad essa appartenente.
Di conseguenza, dovrà essere necessariamente possibile ricavare l’equazione di una retta (in forma esplicita) a partire dalle coordinate di due suoi punti, ed inoltre dovrà anche essere possibile ricavare a partire da tali coordinate il valore del coefficiente angolare della retta in esame. Di questo ci occuperemo nella prossima lezione, dedicata alla definizione di coefficiente angolare di una retta nel piano cartesiano. Buon proseguimento! 🙂
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
