Tangenti ad una parabola condotte da un punto esterno

 - 

Parabola (scuole superiori)

Le equazioni delle rette tangenti ad una parabola condotte da un punto esterno si determinano ricercando i corrispondenti coefficienti angolari. I valori di tali coefficienti sono quelli che rendono nullo il determinante dell’equazione risolvente relativa al sistema formato dall’equazione della parabola e dall’equazione della generica retta passante per il punto esterno.

In questa lezione vedremo come determinare le equazioni delle rette tangenti ad una parabola condotte da un punto esterno alla parabola stessa. Per punto esterno alla parabola intendiamo un punto non appartenente alla parabola stessa e tale da trovarsi al di fuori della regione di piano delimitata dalla parabola.

Le rette tangenti ad una parabola e passanti per un fissato punto esterno alla parabola stessa sono sempre due. Se invece il punto appartiene alla parabola, come abbiamo visto la retta tangente alla parabola in quel punto è unica (vedi la precedente lezione sulla retta tangente ad una parabola in un suo punto). Di conseguenza, imponendo uguale a zero il determinante dell’equazione risolvente, se il punto considerato è esterno alla parabola otterremo sempre due valori per {m}.

L’approccio che qui utilizzeremo per determinare le equazioni delle rette tangenti ad una parabola condotte da un punto esterno è lo stesso di quello già visto nel caso della circonferenza. Tuttavia, poiché l’equazione di una parabola con asse verticale od orizzontale è più semplice di quella della circonferenza, il metodo si presenta nel caso della parabola più semplice da applicare, in quanto sono richiesti dei calcoli decisamente meno pesanti.

L’idea sulla quale si basa il metodo parte dal concetto di intersezione tra una parabola ed una retta. E, come sappiamo, per determinare gli eventuali punti di intersezione tra la retta e la parabola occorre mettere a sistema le rispettive equazioni. Per confronto è possibile ottenere l’equazione risolvente del sistema, e la retta è tangente alla parabola se il determinante dell’equazione risolvente risulta uguale a zero.

Ora, nel nostro caso non sono note le equazioni delle rette tangenti. Tuttavia, come già visto nella lezione precedente è possibile comunque scrivere l’equazione della generica retta passante per il punto esterno considerato. E le rette tangenti cercate sono entrambe esprimibili con tale equazione, per opportuni valori del coefficiente angolare {m}. Così, l’idea è quella di scrivere l’equazione risolvente del sistema contenente le equazioni della parabola e della retta, e quindi imporre il determinante di tale equazione uguale a zero. Ciò che si ottiene è un’equazione di secondo grado nella sola incognita {m}, che una volta risolta fornisce i due valori dei coefficienti angolari, corrispondenti ciascuno ad una retta tangente condotta dal punto esterno dato.

Precisiamo che considerando un punto esterno alla parabola, le formule di sdoppiamento non sono in questo caso applicabili.

Come determinare le equazioni delle rette tangenti ad una parabola e condotte da un punto esterno alla parabola stessa

Consideriamo una parabola ad esempio con asse di simmetria verticale, avente di conseguenza equazione:

\mathscr{P}:y=ax^2+bx+c, \qquad a\neq 0, \quad a,b,c \in \R

Supponiamo inoltre che sia dato un punto {P} esterno alla parabola:

P=(x_P,y_P)

Il punto è tale da non appartenere alla parabola ed è inoltre tale da non trovarsi nella regione di piano delimitata dalla parabola stessa. Sotto tale ipotesi, si può dimostrare che le rette tangenti alla parabola condotte da tale punto sono sempre e solo due. Indichiamo tali rette con {t_1} e {t_2}.

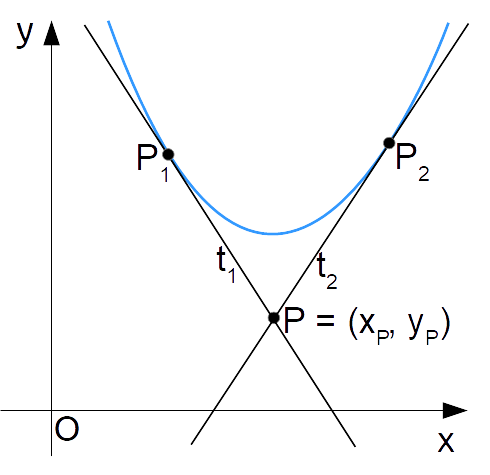
Ora, il nostro obiettivo è determinare le equazioni delle rette {t_1} e {t_2}, tangenti alla parabola rispettivamente nei punti {P_1} e {P_2}.

Poiché le due rette passano per {P}, ciascuna di esse avrà equazione esprimibile nella forma:

t:y-y_P=m(x-x_P)

Tale equazione rappresenta il fascio di rette proprio avente per centro il punto {P}. Così, per determinare le equazioni delle rette tangenti alla parabola e condotte dal punto {P} dovremo determinare i due valori del coefficiente angolare {m} ai quali corrispondono le equazioni di tali rette tangenti.

Da quanto sappiamo sull’intersezione tra una parabola e una retta, per ricercare i punti di intersezione {P_1} e {P_2} bisogna impostare il seguente sistema:

\begin{cases} \mathscr{P}:y=ax^2+bx+c \\ \\ t:y-y_P=m(x-x_P)\end{cases}

Tuttavia, non potendo fissare alcun valore per il coefficiente angolare {m}, non è possibile risolvere il sistema. Ciò non è comunque un problema, poiché non siamo interessati a risolvere il sistema ma soltanto a ricavare i due valori di {m} corrispondenti alle rette tangenti cercate.

Seguendo il metodo già visto nella lezione precedente, esplicitiamo la variabile {y} dalla seconda equazione a sistema:

\begin{cases} \mathscr{P}:y=ax^2+bx+c \\ \\t:y=mx-mx_P+y_P\end{cases}

Dal confronto delle due equazioni a sistema otteniamo l’equazione risolvente:

ax^2+bx+c=mx-mx_P+y_P

ovvero trasportando i termini ed eseguendo dei raccoglimenti:

ax^2+(b-m)x+c+mx_P-y_P=0

Sempre in modo del tutto simile a quanto visto nella precedente lezione, imponendo uguale a zero il determinante di tale equazione, abbiamo:

m^2+(-2b-4ax_P)m+b^2-4ac+4ay_P=0

Tale equazione è nella sola variabile {m} e consente di determinare i valori di {m} corrispondenti alle rette tangenti cercate.

Con un procedimento del tutto simile è possibile scrivere l’equazione risolvente e quindi determinare i valori di {m} corrispondenti alle rette condotte da un punto esterno e tangenti ad una parabola con asse di simmetria orizzontale.

Come visto nella precedente lezione, stiamo attenti al caso di una parabola con asse di simmetria orizzontale. Potrebbe accadere che una delle due tangenti sia verticale e quindi per essa non troveremo alcun valore di {m}. In tale circostanza, imponendo il determinante dell’equazione risolvente uguale a zero otterremo infatti un solo valore di {m}. Ma poiché, lo sottolineiamo, le rette tangenti ad una parabola condotte da un punto esterno sono sempre due, sarà evidente che l’equazione mancante corrisponderà ad una retta verticale, avente equazione {x=x_P} (la retta {t_1} nella figura a seguire).

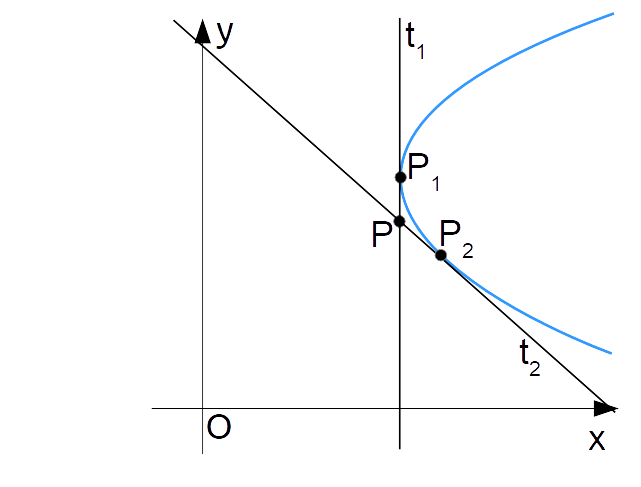
Osserviamo che nella situazione indicata in figura il punto {P_1} coincide con il vertice della parabola.

Nel caso di una parabola con asse di simmetria verticale otterremo invece sempre due valori per il coefficiente angolare {m}, senza che mai si verifichi un simile caso particolare. Infatti, l’equazione {y-y_P=m(x-x_P)} è in grado anche di rappresentare una retta orizzontale (questa si ha come sappiamo per {m=0}).

Mettiamo subito in pratica quanto sin qui visto risolvendo insieme alcuni problemi di esempio.

Esempio 1

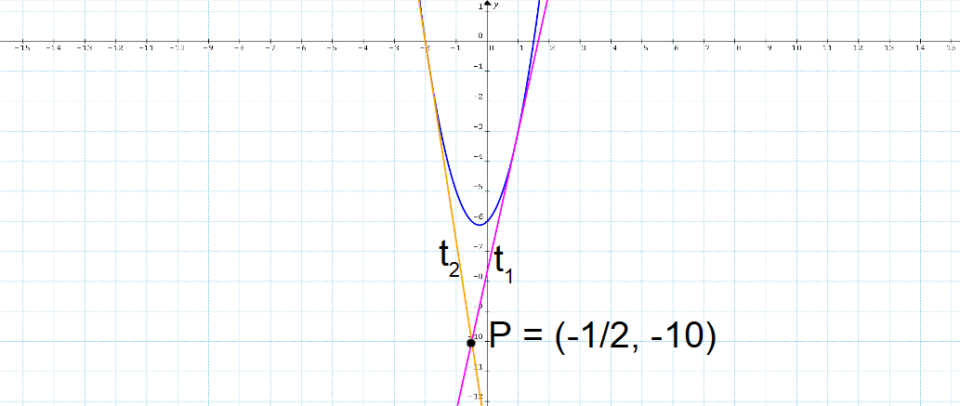
Determinare le equazioni delle rette tangenti alla parabola {\mathscr{P}:y=2x^2+x-6} e condotte dal punto esterno {P=\left( -\dfrac{1}{2}, -10\right)}.

Grazie alla formula della retta passante per un punto con pendenza nota, l’equazione della generica retta passante per il punto {P} è:

t:y-y_P=m(x-x_P)

e quindi, sostituendo le coordinate del punto {P}:

t:y+10=m\left(x+\dfrac{1}{2}\right)

ovvero in forma esplicita:

t: y=mx+\dfrac{1}{2}m-10

Impostiamo il sistema relativo all’intersezione tra la parabola e la generica retta {t} passante per {P}:

\begin{cases} \mathscr{P}:y=2x^2+x-6 \\ \\ t: y=mx+\dfrac{1}{2}m-10\end{cases}

Per confronto otteniamo l’equazione risolvente:

\begin{align*} &2x^2+x-6=mx+\dfrac{1}{2}m-10; \\ \\ & 2x^2+(1-m)x-6-\dfrac{1}{2}m+10=0;\\ \\ & 2x^2+(1-m)x-\dfrac{1}{2}m+4=0\end{align*}

L’equazione è della forma {Ax^2+Bx+C=0} ponendo {A=2, B=1-m, C=-\dfrac{1}{2}m+4}. Imponiamo il determinante uguale a zero (condizione di tangenza alla parabola per la generica retta {t}):

\begin{align*} &B^2-4AC=0; \\ \\ & (1-m)^2-4 \cdot 2 \cdot \left( -\dfrac{1}{2}m+4\right)=0;\\ \\ & 1-2m+m^2+4m-32=0;\\ \\ & m^2+2m-31=0\end{align*}

Abbiamo in questo modo ottenuto un’equazione di secondo grado rispetto alla variabile {m}. Risolvendo tale equazione, è possibile ottenere i due valori di {m} che corrispondono ciascuno alle rette tangenti cercate.

Si tratta di un’equazione di secondo grado in forma normale, che possiamo risolvere utilizzando la formula risolutiva ridottissima:

\begin{align*} &m_{1,2}=-1 \pm \sqrt{1+31}=-1 \pm \sqrt{32}=-1\pm \sqrt{2^5}=-1\pm\sqrt{2^4 \cdot 2}=-1\pm 4\sqrt{2}\end{align*}

Così otteniamo per {m} i due distinti valori reali:

m_1=-1+4\sqrt{2}, \qquad m_2=-1-4\sqrt{2}

Sostituendo tali valori nell’equazione della generica retta passante per {P} è possibile in conclusione determinare le equazioni delle rette tangenti alla parabola condotte per il punto {P}. Abbiamo rispettivamente:

\begin{align*} &t: y=mx+\dfrac{1}{2}m-10 \quad \text{con} \quad m=-1+4\sqrt{2} \\ \\ & \Rightarrow y=(-1+4\sqrt{2})x+\dfrac{1}{2}(-1+4\sqrt{2})-10; \\ \\ & y=(-1+4\sqrt{2})x-\dfrac{1}{2}+2\sqrt{2}-10;\\ \\ & \boxed{t_1: y=(-1+4\sqrt{2})x+2\sqrt{2}-\dfrac{21}{2}}\end{align*}

e:

\begin{align*} &t: y=mx+\dfrac{1}{2}m-10 \quad \text{con} \quad m=-1-4\sqrt{2} \\ \\ & \Rightarrow y=(-1-4\sqrt{2})x+\dfrac{1}{2}(-1-4\sqrt{2})-10; \\ \\ & y=(-1-4\sqrt{2})x-\dfrac{1}{2}-2\sqrt{2}-10;\\ \\ & \boxed{t_2: y=(-1-4\sqrt{2})x-2\sqrt{2}-\dfrac{21}{2}}\end{align*}

E quelle evidenziate nei riquadri sono in conclusione le equazioni delle rette tangenti alla parabola in esame e condotte dal punto {P=\left( -\dfrac{1}{2}, -10\right)}.

Esempio 2

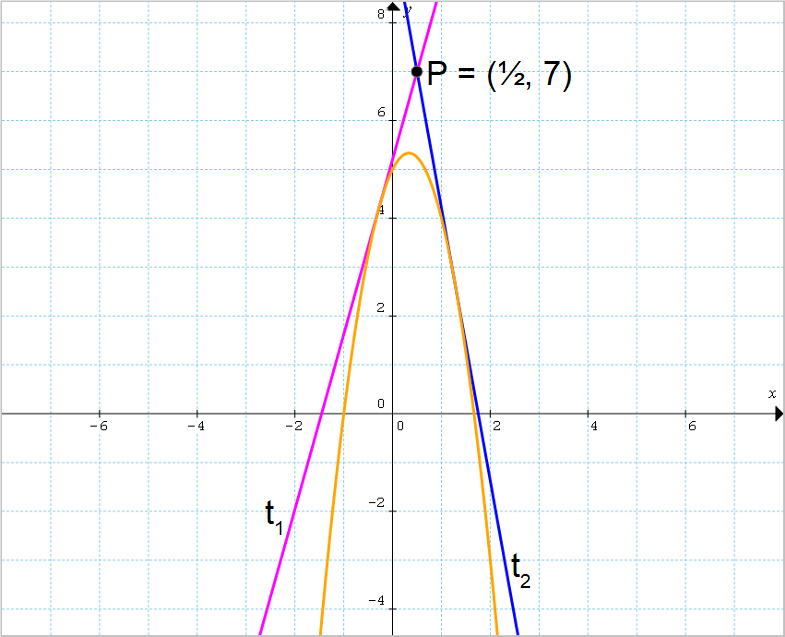
Determinare le equazioni delle rette tangenti alla parabola {\mathscr{P}:y=-3x^2+2x+5} condotte dal punto {P=\left( \dfrac{1}{2}, 7\right)}.

Scriviamo l’equazione in forma esplicita della generica retta passante per il punto {P}:

\begin{align*} &y-7=m\left( x-\dfrac{1}{2}\right);\\ \\ &t: y=mx-\dfrac{1}{2}m+7\end{align*}

Impostiamo il sistema:

\begin{cases} \mathscr{P}:y=-3x^2+2x+5 \\ \\ t: y=mx-\dfrac{1}{2}m+7\end{cases}

Procediamo per confronto in modo da scrivere l’equazione risolvente:

\begin{align*} & -3x^2+2x+5=mx-\dfrac{1}{2}m+7; \\ \\ & -3x^2+(2-m)x+5-7+\dfrac{1}{2}m=0;\\ \\ & -3x^2+(2-m)x+\dfrac{1}{2}m-2=0 \end{align*}

Imponiamo il determinante dell’equazione risolvente uguale a zero:

\begin{align*} &B^2-4AC=0; \\ \\ & (2-m)^2-4 \cdot (-3) \cdot \left( \dfrac{1}{2}m-2\right)=0;\\ \\ & 4-4m+m^2+12 \cdot \left( \dfrac{1}{2}m-2\right)=0;\\ \\ & 4-4m+m^2+6m-24=0;\\ \\ & m^2+2m-20=0\end{align*}

Risolvendo l’equazione appena scritta rispetto ad {m} otteniamo:

m_{1,2}=-1 \pm \sqrt{1+20}=\begin{cases} -1+\sqrt{21} \\ \\ -1-\sqrt{21}\end{cases}

Sostituendo ciascuno dei valori di {m} appena ottenuti nell’equazione della generica retta passante per {P} abbiamo rispettivamente:

\begin{align*} &y=mx-\dfrac{1}{2}m+7 \quad \text{con} \quad m=-1+\sqrt{21} \\ \\ & \Rightarrow \quad y=(-1+\sqrt{21})x+\dfrac{1}{2}-\dfrac{\sqrt{21}}{2}+7; \\ \\ & t_1: y=(-1+\sqrt{21})x+\dfrac{15-\sqrt{21}}{2}\end{align*}

e:

\begin{align*} &y=mx-\dfrac{1}{2}m+7 \quad \text{con} \quad m=-1-\sqrt{21} \\ \\ & \Rightarrow \quad y=(-1-\sqrt{21})x+\dfrac{1}{2}+\dfrac{\sqrt{21}}{2}+7; \\ \\ & t_2: y=(-1-\sqrt{21})x+\dfrac{15+\sqrt{21}}{2}\end{align*}

Abbiamo così determinato le equazioni delle rette {t_1} e {t_2} cercate.

Esempio 3

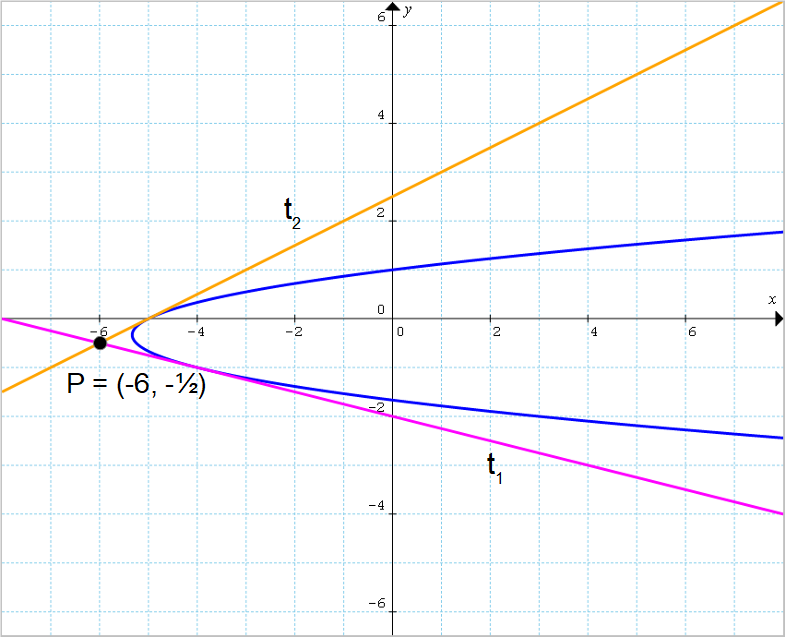
Scrivere le equazioni delle rette tangenti alla parabola {\mathscr{P}:x=3y^2+2y-5} e tali da passare per il punto {P=\left( -6, -\dfrac{1}{2}\right)}.

Il problema è formulato in un altro modo rispetto agli altri esempi, ma si tratta sempre di determinare le equazioni delle rette tangenti ad una parabola e condotte per un punto esterno dato. Osserviamo che in questo caso la parabola ha asse di simmetria orizzontale. Ciò non comporta grandi cambiamenti nel metodo risolutivo, tuttavia dovremo prestare attenzione al fatto che potremmo ottenere un solo valore per il coefficiente angolare {m}. Ed in tal caso, ci ritroveremmo con una seconda retta tangente alla quale non corrisponde alcun valore di {m}, data dalla retta verticale {x=x_P}.

Cominciamo scrivendo l’equazione della generica retta {t} passante per {P}:

t:y+\dfrac{1}{2}=m\left( x+6\right)

Lavoriamo sull’equazione in modo da esplicitare la variabile {x}. Ciò è utile poiché in questo caso l’equazione della parabola è della forma {x=f(y)}. Così esplicitando la variabile {x} dall’equazione della generica retta passante per {P} sarà poi possibile ottenere l’equazione risolvente del sistema per confronto. Abbiamo:

\begin{align*} &y=mx+6m-\dfrac{1}{2}; \\ \\ & mx=y-6m+\dfrac{1}{2};\\ \\ &t: x=\dfrac{1}{m}y-6+\dfrac{1}{2m}, \qquad m \neq 0\end{align*}

La condizione {m \neq 0} non comporta alcun inconveniente. Infatti, ad {m=0} corrisponde una retta orizzontale, la quale è sempre secante ad una parabola con asse di simmetria orizzontale. Di conseguenza, la condizione {m \neq 0} non comporta l’esclusione di una possibile retta tangente alla parabola.

Impostiamo a questo punto il sistema relativo all’intersezione della parabola con la generica retta passante per {P}:

\begin{cases} \mathscr{P}:x=3y^2+2y-5 \\ \\ t: x=\dfrac{1}{m}y-6+\dfrac{1}{2m}\end{cases}

Per confronto possiamo scrivere l’equazione risolvente del sistema:

\begin{align*} &3y^2+2y-5=\dfrac{1}{m}y-6+\dfrac{1}{2m};\\ \\ & 3y^2+\left( 2-\dfrac{1}{m}\right)y-5+6-\dfrac{1}{2m}=0;\\ \\ & 3y^2+2y-\dfrac{1}{m}y+1-\dfrac{1}{2m}=0;\\ \\ &\dfrac{6my^2+4my-2y+2m-1}{\cancel{2m}}=0, \qquad m\neq0;\\ \\ &6my^2+(4m-2)y+2m-1=0  \end{align*}

Abbiamo così ottenuto l’equazione risolvente relativa al sistema. Questa è della forma {Ay^2+By+C} ponendo {A=6m, B=4m-2} e {C=2m-1}.

Imponiamo a questo punto che il determinante dell’equazione risolvente sia uguale a zero. Dato che il coefficiente {B} ha termini tutti con coefficiente pari, possiamo utilizzare per alleggerire i calcoli il {\Delta/4}. Abbiamo:

\begin{align*} & \dfrac{\Delta}{4}=0;\\ \\ &\left( \dfrac{B}{2}\right)^2-AC=0;\\ \\ & (2m-1)^2-6m\cdot(2m-1)=0;\\ \\ & 4m^2-4m+1-12m^2+6m=0;\\ \\ & -8m^2+2m+1=0  \end{align*}

Risolviamo l’equazione rispetto a {m} (formula ridotta):

\begin{align*} &m_{1,2}=\dfrac{-1\pm \sqrt{1-(-8)\cdot1}}{-8}=\dfrac{-1\pm3}{-8}=\begin{cases}-\dfrac{1}{4} \\ \\ \dfrac{1}{2}\end{cases}\end{align*}

Otteniamo così due valori per {m} ai quali corrispondono le equazioni delle due rette tangenti alla parabola condotte per {P}. Avendo ottenuto due valori per {m}, siamo sicuri che non c’è in questo caso una retta tangente mancante.

Ora non resta che riprendere l’equazione della generica retta {t}, ad esempio nella forma:

t:y=mx+6m-\dfrac{1}{2}

e quindi sostituire in essa ciascuno dei valori ottenuti per {m}. Abbiamo:

\begin{align*} &y=mx+6m-\dfrac{1}{2} \quad \text{con} \quad m=-\dfrac{1}{4}\\ \\ & \Rightarrow \quad y=-\dfrac{1}{4}x+6 \cdot\left( -\dfrac{1}{4}\right)-\dfrac{1}{2};\\ \\ & t_1: y=-\dfrac{1}{4}x-2\end{align*}

e infine:

\begin{align*} &y=mx+6m-\dfrac{1}{2} \quad \text{con} \quad m=\dfrac{1}{2}\\ \\ & \Rightarrow \quad y=\dfrac{1}{2}x+6 \cdot \dfrac{1}{2}-\dfrac{1}{2};\\ \\ & t_2: y=\dfrac{1}{2}x+\dfrac{5}{2}\end{align*}

Siamo quindi riusciti a determinare le equazioni delle rette tangenti alla parabola e tali da passare per il punto {P}. In altre parole, le rette {t_1} e {t_2} sono le rette tangenti alla parabola data condotte dal punto esterno {P}.

Esempio 4

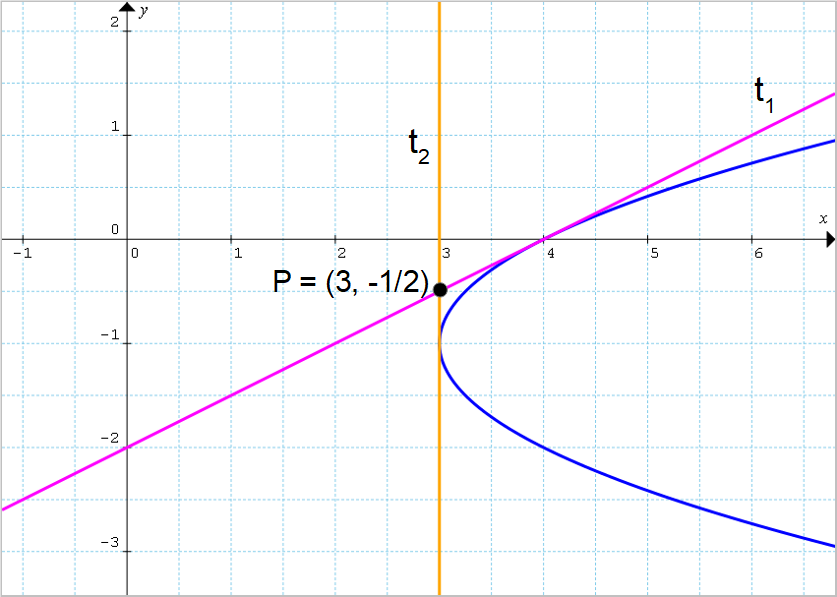
Determinare le equazioni delle rette tangenti alla parabola di equazione {\mathscr{P}:x=y^2+2y+4} e condotte per il punto esterno {P=\left( 3, -\dfrac{1}{2}\right)}.

La parabola è ad asse di simmetria orizzontale. Per cui dovremo prestare attenzione a quanti valori per {m} otterremo. Come ormai sappiamo, potremmo ottenere un solo valore, ma dovremo comunque ricordare che le rette tangenti ad una parabola condotte per un punto esterno alla parabola stessa sono sempre due.

Come al solito, scriviamo l’equazione della generica retta passante per {P}:

t: \left( y+\dfrac{1}{2}\right)=m(x-3)

Riscriviamo l’equazione in modo da esplicitare la variabile {x}:

\begin{align*} &y=mx-3m-\dfrac{1}{2};\\ \\ & mx=y+3m+\dfrac{1}{2};\\ \\ &t: x=\dfrac{1}{m}y+3+\dfrac{1}{2m}, \quad m \neq 0\end{align*}

Impostiamo il sistema come negli esempi precedenti:

\begin{cases} \mathscr{P}:x=y^2+2y+4 \\ \\ t:x=\dfrac{1}{m}y+3+\dfrac{1}{2m} \end{cases}

Per confronto otteniamo l’equazione risolvente:

\begin{align*} & y^2+2y+4=\dfrac{1}{m}y+3+\dfrac{1}{2m}; \\ \\ & y^2+\left( 2-\dfrac{1}{m}\right)y-\dfrac{1}{2m}+1=0\end{align*}

Imponiamo che il determinante dell’equazione risolvente sia nullo:

\begin{align*} &\left( 2-\dfrac{1}{m}\right)^2-4 \cdot 1 \cdot \left( -\dfrac{1}{2m}+1\right)=0;\\ \\ & \cancel{4}-\dfrac{4}{m}+\dfrac{1}{m^2}+\dfrac{2}{m}-\cancel{4}=0;\\ \\ & \dfrac{-4m+1+2m}{\cancel{m^2}}=0, \quad m\neq0;\\ \\ & -2m+1=0 \quad \Rightarrow \quad m=\dfrac{1}{2}\end{align*}

Otteniamo per {m} un unico valore, al quale corrisponde la retta tangente:

\begin{align*} &y=mx-3m-\dfrac{1}{2} \quad \text{con} \quad m=\dfrac{1}{2}\\ \\ & \Rightarrow \quad y=\dfrac{1}{2}x-3 \cdot \dfrac{1}{2}-\dfrac{1}{2};\\ \\ & t_1:y=\dfrac{1}{2}x-2\end{align*}

Ora, attenzione. Abbiamo sin qui ottenuto una sola retta tangente alla parabola, ma come sappiamo le rette tangenti ad una parabola condotte da un punto esterno sono sempre due.

Poiché la parabola ha asse di simmetria orizzontale, siamo evidentemente nel caso in cui una delle due rette tangenti è verticale. E per una retta verticale, il coefficiente angolare non è definito. Ed è questo il motivo per cui abbiamo ottenuto un solo valore di {m}, nonostante l’esistenza di due rette tangenti.

La retta tangente mancante è quindi la retta verticale passante per il punto esterno {P}. E poiché il punto {P} ha ascissa uguale a {3}, la seconda retta tangente ha equazione:

t_2:x=3

Abbiamo così determinato le equazioni di entrambe le rette tangenti cercate.

Conclusioni

Per quanto riguarda questa lezione su come determinare le equazioni delle rette tangenti ad una parabola condotte per un punto esterno alla parabola stessa è tutto.

Prima di salutarci, vogliamo precisare che nel caso in cui venga richiesto di determinare anche le coordinate dei punti di tangenza delle rette rispetto alla parabola, basta tenere conto di quanto visto nella lezione precedente. Così, una volta trovate le equazioni delle rette {t_1} e {t_2}, per conoscere ad esempio le coordinate del punto ove la retta {t_1} è tangente alla parabola, basterà risolvere il sistema dato dall’equazione della retta e dall’equazione della parabola.

Un saluto a tutti voi e buon proseguimento con SìMatematica!