Parabola passante per tre punti

 - 

Parabola (scuole superiori)

L’equazione di una parabola passante per tre punti distinti noti, posto che l’asse sia verticale o orizzontale, si ottiene ricavando i coefficienti a, b, c dell’equazione stessa, mettendo a sistema le condizioni di appartenenza della parabola a ciascuno dei punti dati.

Il metodo per scrivere l’equazione di una parabola passante per tre punti dati è quindi del tutto simile al metodo già visto per scrivere l’equazione di una circonferenza passante per tre punti. Tuttavia, nel caso della parabola, oltre alle coordinate dei tre punti è anche necessario sapere se l’asse della parabola è orizzontale o verticale. Diversamente, la parabola non risulterebbe univocamente identificata nel piano.

Così, nota la disposizione dell’asse della parabola (verticale od orizzontale), è possibile individuare univocamente una parabola del piano a partire dalle coordinate di tre distinti punti appartenenti alla parabola stessa.

A partire da questa lezione ci occupiamo quindi del problema dell’individuazione delle condizioni per scrivere l’equazione di una parabola. In altre parole, in questa lezione e nelle successive mostreremo quali sono le condizioni necessarie e sufficienti per individuare una parabola nel piano. Il passaggio di una parabola per tre distinti punti del piano, ovvero l’argomento di questa lezione, è soltanto una fra le possibili condizioni che consentono di individuare in maniera univoca una parabola nel piano cartesiano. Tra l’altro, conosciamo già una condizione, ed è data dalla conoscenza delle coordinate del fuoco e dell’equazione della direttrice della parabola. A partire da tali dati, infatti, è possibile ottenere l’equazione della parabola utilizzando la sua definizione come luogo geometrico. Di questo ci siamo occupati nelle prime lezioni.

Vediamo subito il metodo generale ed un paio di esempi su come determinare l’equazione di una parabola per tre punti distinti del piano.

Come determinare l’equazione di una parabola con asse verticale od orizzontale passante per tre punti distinti del piano

Supponiamo di avere una parabola con asse di simmetria verticale, della quale non sia nota l’equazione. Possiamo comunque scriverne l’equazione in forma generale:

y=ax^2+bx+c, \quad a \neq 0, \quad a,b,c \in \R

ove i coefficienti {a,b,c} sono incognite.

Pur non conoscendo l’equazione, sono note le coordinate di tre punti appartenenti alla parabola:

P_1=(x_1,y_1), \quad P_2=(x_2,y_2), \quad P_3=(x_3,y_3)

Il nostro obiettivo è scrivere l’equazione della parabola in esame. Ma per fare ciò, occorre ricavare i valori dei coefficienti {a,b,c} corrispondenti ai tre punti dati.

Ricordiamo che se un certo punto appartiene alla parabola, le sue coordinate devono soddisfare l’equazione della parabola stessa. Così, se il punto {P_1=(x_1, y_1)} appartiene alla parabola, le sue coordinate devono soddisfare l’equazione della parabola, ovvero dovrà risultare verificata l’uguaglianza:

y_1=ax_1^2+bx_1+c \qquad \text{condizione di appartenza per }P_1

Allo stesso modo, per il punto {P_2=(x_2, y_2)} abbiamo:

y_2=ax_2^2+bx_2+c \qquad \text{condizione di appartenenza per }P_2

Infine, per il punto {P_3=(x_3, y_3)}:

y_3=ax_3^2+bx_3+c \qquad \text{condizione di appartenenza per }P_3

Ora, le tre condizioni devono valere contemporaneamente. Per cui, possiamo scrivere un sistema contenente tutte e tre le uguaglianze corrispondenti alle condizioni di appartenenza dei punti alla parabola:

\begin{cases}y_1=ax_1^2+bx_1+c \\ \\ y_2=ax_2^2+bx_2+c \\ \\ y_3=ax_3^2+bx_3+c \end{cases} \qquad \text{parabola con asse verticale}

Si tratta di un sistema lineare di tre equazioni e nelle tre incognite {a,b,c}. Risolvendo il sistema si ottengono i tre valori dei coefficienti {a,b,c}, che consentono di scrivere l’equazione della parabola in esame.

Nel caso di una parabola con asse di simmetria orizzontale, il discorso è del tutto simile. In particolare, per ricavare i coefficienti {a,b,c} basterà risolvere il sistema:

\begin{cases} x_1=ay_1^2+by_1+c \\ \\ x_2=ay_2^2+by_2+c \\ \\ x_3=ay_3^2+by_3+c\end{cases} \qquad \text{parabola con asse orizzontale}

Come possiamo vedere, ciascuna equazione a sistema corrisponde alla forma generale dell’equazione di una parabola con asse di simmetria orizzontale.

Vediamo subito degli esempi, relativi rispettivamente al caso di una parabola con asse verticale e di una parabola con asse orizzontale.

Esempio 1

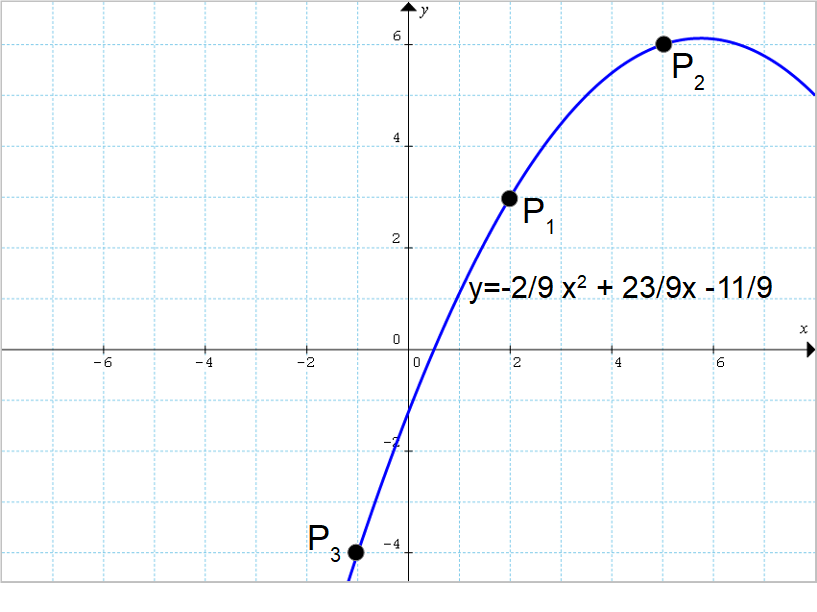
Determinare l’equazione della parabola con asse verticale passante per i punti {P_1=(2,3), P_2=(5,6)} e {P_3=(-1,-4)}.

Poiché la parabola ha asse di simmetria verticale, l’equazione della parabola da utilizzare per scrivere le condizioni di appartenenza è:

y=ax^2+bx+c, \qquad a\neq0, \quad a,b,c \in \R

Sostituendo nell’equazione le coordinate di ciascun punto, otteniamo le tre condizioni, che mettiamo direttamente a sistema:

\begin{cases}y_1=ax_1^2+bx_1+c \\ \\ y_2=ax_2^2+bx_2+c \\ \\ y_3=ax_3^2+bx_3+c \end{cases}

ovvero, sostituendo i valori delle coordinate di ciascun punto:

\begin{cases} 3=a\cdot2^2+b\cdot2+c \\ \\ 6=a\cdot5^2+b\cdot5+c \\ \\ -4=a \cdot (-1)^2+b \cdot (-1)+c\end{cases}

Svolgiamo i calcoli e riscriviamo il sistema in forma normale:

\begin{cases} 4a+2b+c=3 \\ \\ 25a+5b+c=6 \\ \\ a-b+c=-4\end{cases}

Proviamo a risolvere il sistema per riduzione. Cominciamo sottraendo la terza equazione alla prima. Mettiamo la nuova equazione che così otteniamo al posto della prima equazione:

\begin{cases} 4a-a+2b+b+\cancel{c}-\cancel{c}=3+4 \quad \rightarrow \quad 3a+3b=7 \\ \\ 25a+5b+c=6 \\ \\ a-b+c=-4\end{cases}

Proseguiamo sottraendo la terza equazione alla seconda. Mettiamo la nuova equazione che così si ottiene al posto della seconda equazione a sistema:

\begin{cases}  3a+3b=7 \\ \\ 25a-a+5b+b+\cancel{c}-\cancel{c}=6+4 \quad \rightarrow \quad 24a+6b=10 \\ \\ a-b+c=-4\end{cases}

Ora mettiamo da parte temporaneamente la terza equazione e risolviamo il sistema considerando soltanto le prime due equazioni, ritrovandoci con un sistema di due equazioni in due incognite. Procediamo per sostituzione.

\begin{cases}  3a+3b=7 \quad \rightarrow \quad a=\dfrac{7-3b}{3}; \qquad  a=\dfrac{7-3\cdot \dfrac{23}{9}}{3}=-\dfrac{2}{9}\\ \\  \cancel{24}^{8}\left( \dfrac{7-3b}{\cancel{3}}\right)+6b=10 \quad \rightarrow \quad56-24b+6b=10 \quad \rightarrow \quad b=\dfrac{23}{9}  \\ \\\dots \end{cases}

A questo punto recuperiamo la terza equazione, grazie alla quale è possibile ricavare il valore di {c}:

\small a-b+c=-4 \quad \Rightarrow \quad c=-4-a+b \quad \Rightarrow \quad c=-4+\dfrac{2}{9}+\dfrac{23}{9}=-\dfrac{11}9{}

Abbiamo così ottenuto i valori dei coefficienti {a,b,c}, e possiamo scrivere l’equazione della parabola cercata. Poiché la parabola è ad asse verticale, la sua equazione avrà forma generale:

y=ax^2+bx+c, \qquad a\neq0, \quad a,b,c \in \R

e quindi sostituendo i valori dei coefficienti {a,b,c } possiamo scrivere in conclusione:

y=-\dfrac{2}{9}x^2+\dfrac{23}{9}x-\dfrac{11}{9}

Ed ecco l’equazione della parabola con asse verticale passante per i tre punti dati.

Esempio 2

Scrivere l’equazione della parabola con asse di simmetria orizzontale passante per i punti {P_1=(3,1), P_2=(3,-1)} e {P_3=(5, \sqrt{2})}.

La parabola è con asse di simmetria orizzontale e quindi con equazione in forma generale:

x=ay^2+by+c, \qquad a\neq0, \quad a,b,c \in \R

Impostiamo il sistema contenente le tre condizioni di appartenenza di ciascun punto alla parabola:

\begin{cases} x_1=ay_1^2+by_1+c \\ \\ x_2=ay_2^2+by_2+c \\ \\ x_3=ay_3^2+by_3+c\end{cases} 

Sostituendo in ciascuna equazione le coordinate del punto corrispondente abbiamo:

\begin{cases} 3=a\cdot 1^2+b \cdot 1+c \\ \\ 3=a \cdot (-1)^2+b \cdot (-1)+c \\ \\ 5 =a \cdot (\sqrt{2})^2+b \cdot \sqrt{2}+c\end{cases} 

ovvero:

\begin{cases} a+b+c=3 \\ \\ a-b+c=3 \\ \\ 2a+\sqrt{2}b+c=5\end{cases}

Nel precedente esempio abbiamo utilizzato il metodo di riduzione. Stavolta risolviamo il sistema utilizzando il metodo di Cramer.

Il sistema si presenta in forma normale e quindi il metodo è correttamente applicabile. Cominciamo calcolando il determinante della matrice dei coefficienti (regola di Sarrus):

\begin{align*} & D=\det \begin{pmatrix} 1 & 1 & 1 \\ 1 &-1 &1 \\ 2 & \sqrt{2} & 1\end{pmatrix} = \\ \\ & =1 \cdot (-1) \cdot 1 + 1 \cdot 1 \cdot 2 + 1 \cdot 1 \cdot \sqrt{2}-2 \cdot (-1) \cdot 1 - \sqrt{2} \cdot 1 \cdot 1 -1 \cdot 1 \cdot 1 =\\ \\ & =-1+2+\sqrt{2}+2-\sqrt{2}-1=2\end{align*}

Proseguiamo con i determinanti {D_a, D_b} e {D_c}, relativi alle matrici che si ottengono mettendo la colonna dei termini noti al posto rispettivamente della prima, della seconda e della terza colonna della matrice dei coefficienti.

\begin{align*} &D_a= \det \begin{pmatrix} 3 & 1 & 1 \\ 3 & -1 & 1 \\ 5 & \sqrt{2} & 1\end{pmatrix}=\\ \\ & =3 \cdot (-1) \cdot 1 + 1 \cdot 1 \cdot 5 + 1 \cdot 3 \cdot \sqrt{2} - 5 \cdot (-1) \cdot 1 -\sqrt{2} \cdot 1 \cdot 3 - 1 \cdot 3 \cdot 1=\\ \\ & -3+5+3\sqrt{2}+5-3\sqrt{2}-3=4; \\ \\  &D_b=\det \begin{pmatrix} 1 & 3 & 1 \\ 1 &3 & 1 \\ 2 & 5 & 1\end{pmatrix}=\\ \\ & =1\cdot3 \cdot 1 + 3 \cdot 1 \cdot 2 +1 \cdot 1 \cdot 5 - 2 \cdot 3 \cdot 1 -5 \cdot 1 \cdot 1-1 \cdot 1 \cdot 3=\\ \\ & =3+6+5-6-5-3=0; \\ \\ &D_c=\det \begin{pmatrix}1 & 1 & 3 \\ 1 & -1 & 3 \\ 2 &\sqrt{2} & 5 \end{pmatrix}=\\ \\ & =1 \cdot (-1) \cdot 5 +1 \cdot 3 \cdot 2 +3 \cdot 1 \cdot \sqrt{2} -2 \cdot (-1) \cdot 3 -\sqrt{2} \cdot 3 \cdot 1-5\cdot1 \cdot 1=\\ \\ & =-5+6+3\sqrt{2}+6-3\sqrt{2}-5=2 \end{align*}

Così per il sistema otteniamo le soluzioni:

\begin{align*} &a=\dfrac{D_a}{D}=\dfrac{4}{2}=2; \qquad b=\dfrac{D_b}{D}=0; \\ \\ & c=\dfrac{D_c}{D}=\dfrac{2}{2}=1\end{align*}

Disponendo dei valori dei coefficienti {a,b,c} possiamo in conclusione scrivere l’equazione della parabola data:

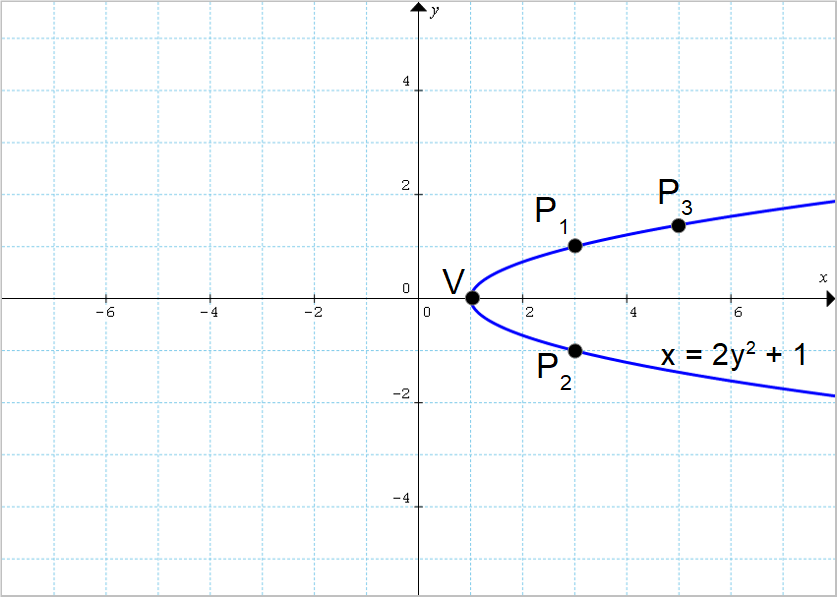
x=2y^2+1

Osserviamo che nella parabola il termine in {y} è mancante, in quanto effettivamente abbiamo {b=0}. Di conseguenza, la parabola ha vertice appartenente all’asse {x} (vedi il paragrafo “parabola con vertice appartenente ad un asse coordinato” della lezione sulla parabola passante per l’origine).

Per questa lezione sulla parabola passante per tre punti è tutto. Nella prossima lezione vedremo come scrivere l’equazione di una parabola a partire dalle coordinate del fuoco e del vertice. Buon proseguimento con SìMatematica!