Per scrivere l’equazione di una parabola con fuoco e vertice noti è possibile ricavare i coefficienti a, b, c mettendo a sistema delle uguaglianze contenenti le espressioni delle coordinate del fuoco e del vertice, o in alternativa ricavare la distanza con segno d relativa alla retta direttrice, e quindi determinare l’equazione della parabola dalla definizione come luogo geometrico.
Proseguiamo le lezioni relative alle condizioni per determinare l’equazione di una parabola mostrando come trovare l’equazione di una parabola a partire dalle coordinate del fuoco e del vertice. Nella precedente lezione abbiamo visto invece come determinare l’equazione di una parabola a partire dalle coordinate di tre punti ad essa appartenenti, essendo nota la disposizione dell’asse della parabola stessa (verticale od orizzontale).
Il primo metodo che utilizzeremo si basa sul fatto che le coordinate del fuoco e del vertice sono note. Così, a partire dalle espressioni delle coordinate del fuoco e del vertice viste nelle precedenti lezioni, sarà possibile uguagliare ciascuna di tali espressioni al valore della coordinata corrispondente. Infine basterà mettere a sistema dette uguaglianze, ricavando i coefficienti a, b, c grazie ai quali sarà possibile scrivere l’equazione della parabola cercata.
Il secondo metodo che proporremo per trovare l’equazione di una parabola conoscendo il fuoco e il vertice consiste nel ricavare la distanza con segno d della direttrice rispetto all’opportuno asse coordinato (ciò dipende dal fatto che la parabola sia ad asse verticale od orizzontale). In particolare, l’idea è quella di ricavare la distanza d, ad esempio nel caso di una parabola con asse verticale, a partire dalle ordinate del fuoco e del vertice. A tal punto, ricavata d è possibile scrivere l’equazione della parabola sfruttando la sua definizione di luogo geometrico, poiché infatti le coordinate del fuoco e l’equazione della direttrice risultano ormai note.
Ma passiamo subito alla spiegazione teorica dei due metodi e ad esempi pratici su come trovare l’equazione di una parabola a partire dalle coordinate del fuoco e del vertice.
Come trovare l’equazione di una parabola con fuoco e vertice noti
Consideriamo entrambi i casi di una parabola con asse verticale ed orizzontale, aventi in generale rispettivamente equazione:
y=ax^2+bx+c \qquad \text{asse verticale}e:
x=ay^2+by+c \qquad \text{asse orizzontale}con {a \neq 0} e {a,b,c \in \R}.
L’obiettivo in entrambi i casi è scrivere l’equazione della parabola. I dati di partenza sono le coordinate del fuoco e del vertice della parabola stessa.
Nel seguito considereremo separatamente ciascun caso, utilizzando ognuno dei due possibili metodi.
Parabola con fuoco e vertice: metodo basato sulle espressioni delle coordinate del fuoco e del vertice
Cominciamo dal caso di una parabola con asse di simmetria verticale, la cui equazione ha forma generale:
y=ax^2+bx+c
ove i coefficienti {a,b,c} sono da ricavare. Non è quindi nota l’equazione della parabola nel caso specifico, ma sono noti i valori delle coordinate del fuoco e del vertice della parabola stessa:
F=(x_F,y_F); \qquad V=(x_V,y_V)
Ricordando le formule per le coordinate del fuoco e del vertice relative ad una parabola con asse verticale, possiamo scrivere le uguaglianze:
\begin{align*} &-\dfrac{b}{2a}=x_F; \qquad \dfrac{1-\Delta}{4a}=y_F; \qquad -\dfrac{\Delta}{4a}=y_V\end{align*}Ricordiamo che in una parabola con asse verticale l’ascissa del fuoco e del vertice coincidono. Per cui relativamente all’espressione {-\dfrac{b}{2a}}, che esprime entrambe le ascisse, abbiamo scritto un’unica uguaglianza.
Ora, poiché {\Delta = b^2-4ac}, ciascuna uguaglianza contiene i tre coefficienti {a,b,c}. Quindi tali uguaglianze possono essere utilizzate per ricavare i valori dei coefficienti {a,b,c}, e quindi scrivere l’equazione della parabola cercata.
In particolare, dato che le uguaglianze devono valere contemporaneamente, l’idea è quella di metterle a sistema:
\begin{cases}-\dfrac{b}{2a}=x_F \\ \\ \dfrac{1-\Delta}{4a}=y_F\\ \\ -\dfrac{\Delta}{4a}=y_V\end{cases}ovvero esplicitando {\Delta}:
\begin{cases}-\dfrac{b}{2a}=x_F \\ \\ \dfrac{1-b^2+4ac}{4a}=y_F\\ \\ \dfrac{4ac-b^2}{4a}=y_V\end{cases} \qquad \small\text{parabola con asse verticale}Si tratta di un sistema non lineare (infatti l’incognita {b} compare con grado superiore al primo e l’incognita {a} figura anche a denominatore). Per risolvere il sistema, possiamo comunque procedere per sostituzione.
Vediamo subito un esempio.
Esempio 1
Scrivere l’equazione della parabola avente fuoco {F=(2,5)} e vertice {V=(2,9).}
La parabola in esame è ad asse verticale poiché il fuoco e il vertice condividono lo stesso valore dell’ascissa.
Scriviamo il sistema che permette di ricavare i coefficienti {a,b,c}, che nel nostro caso è:
\begin{cases}-\dfrac{b}{2a}=2 \\ \\ \dfrac{1-b^2+4ac}{4a}=5\\ \\ \dfrac{4ac-b^2}{4a}=9\end{cases}Osserviamo che ai secondi membri di ciascuna equazione abbiamo sostituito rispettivamente l’ascissa del fuoco, l’ordinata del fuoco e l’ordinata del vertice.
Cominciamo ricavando un’espressione per {b} dalla prima equazione:
\begin{cases}-\dfrac{b}{2a}=2 \quad \rightarrow \quad b=-4a, \quad a \neq 0 \\ \\ \dfrac{1-b^2+4ac}{4a}=5\\ \\ \dfrac{4ac-b^2}{4a}=9\end{cases}Osserviamo che la condizione {a \neq 0} è sempre rispettata, poiché in un’equazione di una parabola verticale (od orizzontale) il coefficiente {a} è per definizione diverso da zero. Eviteremo quindi nel seguito di ripetere tale condizione ogni volta.
A questo punto mettiamo da parte la prima equazione e sostituiamo l’espressione appena ottenuta per {b} nella seconda e terza equazione:
\begin{cases} \dots \\ \\ \dfrac{1-(-4a)^2+4ac}{4a}=5\\ \\ \dfrac{4ac-(4a)^2}{4a}=9\end{cases} \quad \Rightarrow \quad \begin{cases} \dots \\ \\ 1-16a^2+4ac-20a=0 \\ \\ 4ac-16a^2-36a=0\end{cases}Ora esplicitiamo la quantità {4ac} da entrambe le equazioni, quindi procediamo per confronto:
\begin{cases} \dots \\ \\ 4ac=20a+16a^2-1 \\ \\ 4ac=16a^2+36a\end{cases}Consideriamo separatamente l’equazione che si ottiene per confronto:
\begin{align*} &20a+\cancel{16a^2}-1=\cancel{16a^2}+36a; \\ \\ & (36-20)a=-1; \\ \\ & 16a=-1 \quad \Rightarrow \quad a=-\dfrac{1}{16}\end{align*}Sostituiamo l’equazione ottenuta ad esempio alla seconda equazione a sistema:
\begin{cases} \dots \\ \\ a=-\dfrac{1}{16} \\ \\ 4ac=16a^2+36a\end{cases}Ora ricaviamo la {c} dalla terza equazione:
\begin{cases} \dots \\ \\ a=-\dfrac{1}{16} \\ \\ 4ac=16a^2+36a \quad \rightarrow \: c=\dfrac{\cancel{4a}(4a+9)}{\cancel{4a}} \quad \rightarrow \: c=\dfrac{35}{4}\end{cases}A questo punto non resta che riprendere la prima equazione, in modo da ricavare il valore di {b}:
\begin{cases} b=-4a \quad \rightarrow \: b=-4 \cdot \left( -\dfrac{1}{16}\right) \quad \rightarrow \: b=\dfrac{1}{4}\\ \\ a=-\dfrac{1}{16} \\ \\ c=\dfrac{35}{4}\end{cases}Ora disponiamo dei valori di tutti e tre i coefficienti {a,b,c}. Sostituendo tali valori nella forma generica dell’equazione di una parabola con asse verticale otteniamo in conclusione l’equazione:
y=-\dfrac{1}{16}x^2+\dfrac{1}{4}x+\dfrac{35}{4}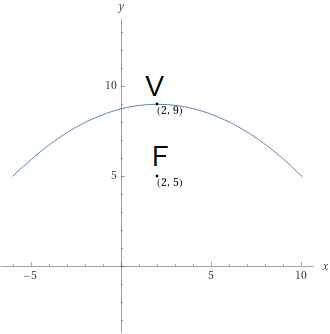
Per quanto riguarda il caso di una parabola con asse orizzontale, i ragionamenti da fare sono molto simili a quelli sin qui visti. In particolare, riprendendo le formule relative alle coordinate del fuoco e del vertice di una parabola con asse di simmetria orizzontale abbiamo:
x_F=\dfrac{1-\Delta}{4a}; \qquad y_F=-\dfrac{b}{2a}; \qquad x_V=-\dfrac{\Delta}{4a}Mettendo le uguaglianze a sistema ed infine esplicitando il {\Delta} abbiamo:
\begin{cases} -\dfrac{b}{2a}=y_F \\ \\ \dfrac{1-b^2+4ac}{4a}=x_F \\ \\ \dfrac{4ac-b^2}{4a}=x_V\end{cases} \qquad \small\text{parabola con asse orizzontale}Il sistema ottenuto è molto simile a quello relativo ad una parabola con asse verticale, differendo soltanto per i secondi membri. In particolare, confrontando i due casi le lettere {x} e {y} risultano scambiate fra loro.
Vediamo subito un esempio su come trovare l’equazione di una parabola con asse orizzontale a partire dalle coordinate del fuoco e del vertice.
Esempio 2
Determinare l’equazione della parabola avente fuoco {F=(-3, 5)} e vertice {V=(1,5)}.
Osserviamo che la parabola è ad asse di simmetria orizzontale in quanto fuoco e vertice condividono la stessa ordinata. Ciò significa che il fuoco e il vertice appartengono alla stessa retta orizzontale, che è l’asse di simmetria della parabola.
Scriviamo il sistema che permette di ricavare i coefficienti {a,b,c}:
\begin{cases} -\dfrac{b}{2a}=5 \\ \\ \dfrac{1-b^2+4ac}{4a}=-3 \\ \\ \dfrac{4ac-b^2}{4a}=1\end{cases}Attenzione a sostituire correttamente i valori nei secondi membri.
Il metodo per risolvere il sistema è del tutto simile a quello del caso precedente. Si procede per sostituzione ricavando per prima cosa un’espressione per {b}. Nei passaggi omettiamo le condizioni {a \neq 0} poiché queste sono soddisfatte necessariamente.
\begin{cases} -\dfrac{b}{2a}=5 \quad \rightarrow \quad b=-10a \\ \\ \dfrac{1-100a^2+4ac}{4a}=-3 \quad \rightarrow \quad 4ac=100a^2-1-12a \\ \\ \dfrac{4ac-100a^2}{4a}=1 \quad \rightarrow \quad 4ac=100a^2+4a\end{cases}Procedendo per confronto:
\begin{cases} b=-10a; \qquad b=-10 \cdot \left( -\dfrac{1}{16}\right) \quad \rightarrow \quad b=\dfrac{5}{8} \\ \\ \cancel{100a^2}-1-12a=\cancel{100a^2}+4a \quad \rightarrow \quad a=-\dfrac{1}{16} \\ \\ c= \dfrac{\cancel{4a}(25a+1)}{\cancel{4a}} \quad \rightarrow \: c=\dfrac{-25+16}{16}=-\dfrac{9}{16}\end{cases}Di conseguenza, sostituendo i valori ottenuti per i coefficienti {a,b,c} nell’equazione di una generica parabola con asse orizzontale otteniamo in conclusione l’equazione:
x=-\dfrac{1}{16}y^2+\dfrac{5}{8}y-\dfrac{9}{16}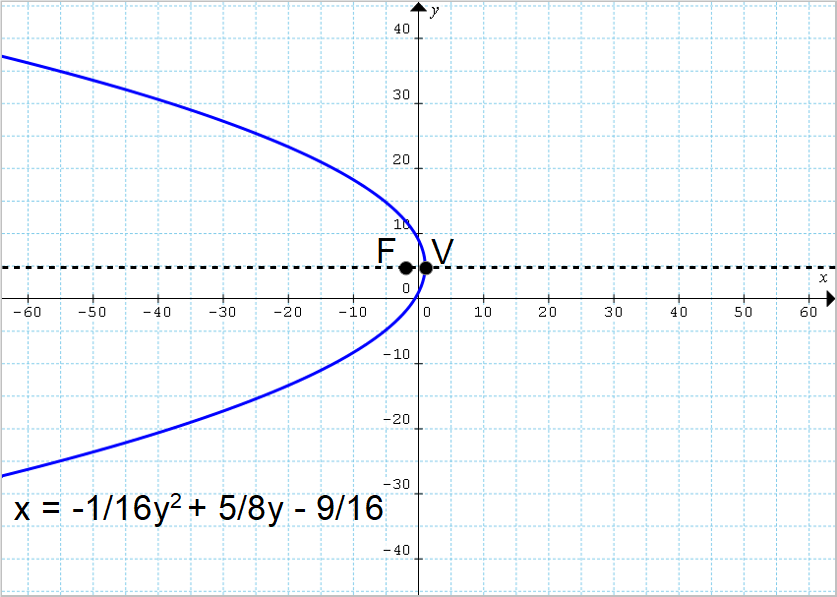
Equazione di una parabola con fuoco e vertice ricavando la distanza con segno d
Il metodo sin qui visto presenta l’inconveniente di dover ricordare le formule delle coordinate del fuoco e del vertice di una parabola, ed inoltre richiede di dover impostare e risolvere un sistema non lineare. Vogliamo allora presentare un metodo alternativo, che consente di scrivere l’equazione della parabola in esame ricavando la distanza con segno {\boldsymbol{d}} della direttrice rispetto all’asse {x} (nel caso di una parabola con asse verticale) o rispetto all’asse {y} (parabola con asse orizzontale).
Metodo della distanza con segno d nel caso di una parabola con asse verticale
Consideriamo una parabola con asse di simmetria verticale, della quale siano note le coordinate del fuoco e del vertice. Il nostro obiettivo è determinare l’equazione della parabola.
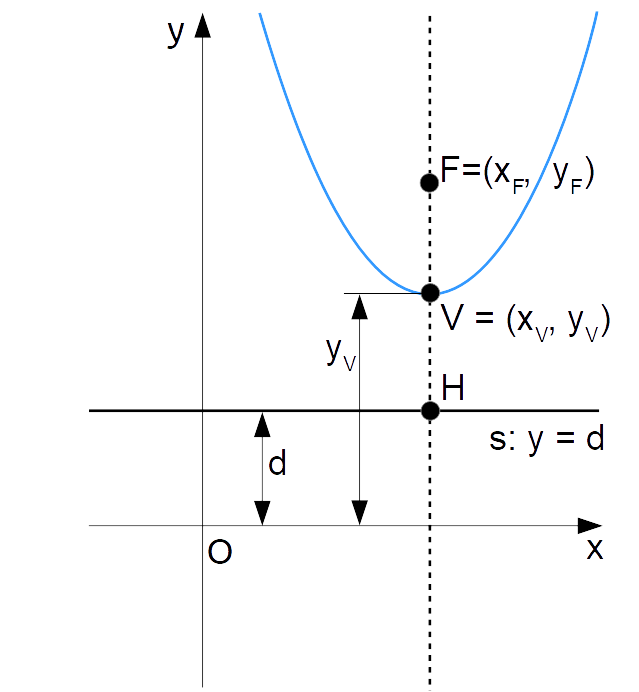
Per poter scrivere l’equazione della parabola, basta ricavare la distanza con segno {d}. A tal punto, infatti, il fuoco e l’equazione della direttrice risulteranno noti, e potremo determinare l’equazione della parabola sfruttando la definizione come luogo geometrico.
Osserviamo che per la definizione di parabola come luogo geometrico, essendo il vertice {V} un punto appartenente alla parabola, si ha:
\overline{FV}=\overline{VH}Così potremo esprimere la distanza con segno {d} come:
d=y_V-\overline{VH}=y_V-\overline{FV}Ora, per ottenere una relazione valida in tutti i casi (direttrice al di sopra o al di sotto dell’asse {x}, concavità della parabola rivolta verso l’alto o verso il basso), occorre considerare non la distanza {\overline{FV}} ma la lunghezza algebrica {FV}, data da {FV=y_V-y_F} (vedi: distanza tra due punti sulla retta). In tal modo, la distanza {d} è esprimibile come:
d=y_V+(\overbrace{y_V-y_F}^{FV}) \quad \Rightarrow \quad \boxed{d=2y_V-y_F}Attenzione: abbiamo scritto {y_V+(y_V-y_F)} e non {y_V-(y_V-y_F)} poiché la quantità {y_V-y_F} è nel caso in figura negativa. E sempre da come si può vedere dalla figura, {d} deve necessariamente essere una quantità positiva minore di {y_V} (anch’essa positiva).
Per una parabola con asse di simmetria verticale la distanza con segno {d} della direttrice rispetto all’asse delle {x} è data da:{d=2y_V-y_F}ove {y_V} è l’ordinata del vertice mentre {y_F} è l’ordinata del fuoco della parabola.
Come verifica dell’uguaglianza appena ricavata, esprimiamo le ordinate del fuoco e del vertice di una parabola con asse verticale mediante le formule:
y_F=\dfrac{1-\Delta}{4a}; \qquad y_V=-\dfrac{\Delta}{4a}Sostituendo tali espressioni nel secondo membro dell’uguaglianza da verificare, abbiamo:
\begin{align*} &2y_V-y_F=2 \cdot\left( -\dfrac{\Delta}{4a}\right)-\dfrac{1-\Delta}{4a}=\dfrac{-2\Delta-1+\Delta}{4a}=\\ \\ & =\dfrac{-\Delta-1}{4a}=\dfrac{-1\cdot(\Delta+1)}{4a}=-\dfrac{1+\Delta}{4a}=d\end{align*}Ma in questo modo abbiamo ritrovato l’espressione corrispondente alla distanza con segno {d}. Infatti, come visto nelle precedenti lezioni si ha {d=-\dfrac{1+\Delta}{4a}}.
Così in conclusione l’uguaglianza {d=2y_V-y_F} relativa ad una parabola con asse verticale risulta sempre verificata.
Ora, una volta noto il valore della distanza con segno {d}, possiamo arrivare all’equazione della parabola partendo dalla definizione di parabola come luogo geometrico. Nel nostro caso è in particolare utile l’uguaglianza:
(x_F-x)^2+(y_F-y)^2=(y-d)^2
per la quale la distanza tra un punto qualunque della parabola ed il fuoco è uguale alla distanza tra quello stesso punto della parabola e la direttrice (vedi: parabola con asse verticale).
Sostituendo in tale uguaglianza i valori delle coordinate del fuoco e della distanza {d} e svolgendo i calcoli è possibile infine scrivere l’equazione della parabola in esame.
Vediamo subito un esempio.
Esempio 3
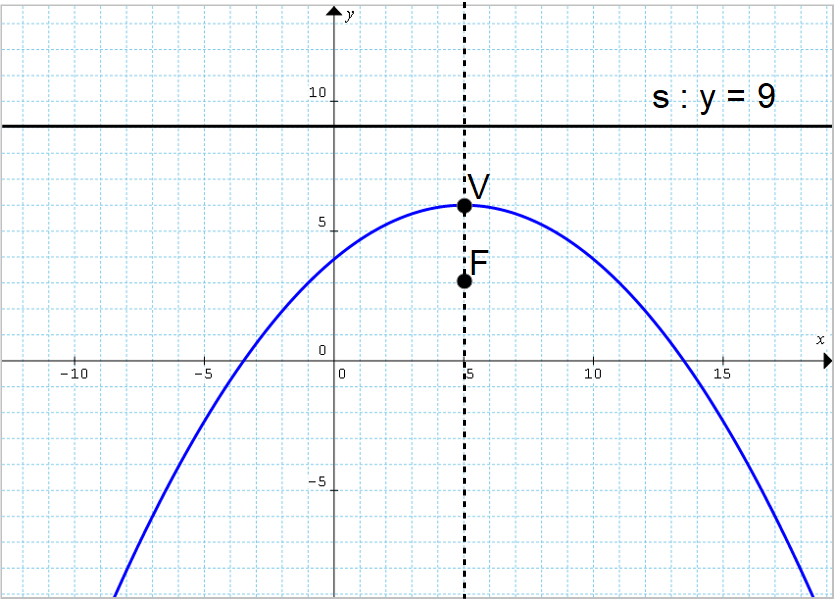
Determinare l’equazione della parabola avente fuoco {F=(5,3)} e vertice {V=(5,6)}.
La parabola è ad asse di simmetria verticale poiché il fuoco e il vertice condividono la stessa ascissa, ovvero appartengono alla stessa retta verticale.
Cominciamo calcolando la distanza {d}:
d=2y_V-y_F=2 \cdot 6-3=12-3=9
A questo punto scriviamo l’uguaglianza relativa ad una parabola con asse verticale come luogo geometrico:
(x_F-x)^2+(y_F-y)^2=(y-d)^2
Sostituendo i valori delle coordinate del fuoco e della distanza con segno {d} abbiamo:
\begin{align*} &(5-x)^2+(3-y)^2=(y-9)^2\end{align*}Sviluppiamo i quadrati di un binomio e quindi trasportiamo opportunamente i termini:
\begin{align*} &25-10x+x^2+9-6y+\cancel{y^2}=\cancel{y^2}-18y+81;\\ \\ &-6y+18y=81-25+10x-x^2-9;\\ \\ & 12y=-x^2+10x+47;\\ \\ & y=-\dfrac{1}{12}x^2+\dfrac{5}{6}x+\dfrac{47}{12} \end{align*}Questa è in conclusione l’equazione della parabola cercata.
Ora, prestiamo attenzione al fatto che la formula {d=2y_V-y_F} è valida soltanto per le parabole con asse verticale. Per quanto riguarda le parabole con asse di simmetria orizzontale valgono invece le considerazioni a seguire.
Metodo della distanza con segno d nel caso di una parabola con asse orizzontale
Consideriamo una parabola con asse di simmetria orizzontale, con coordinate del fuoco e del vertice note.
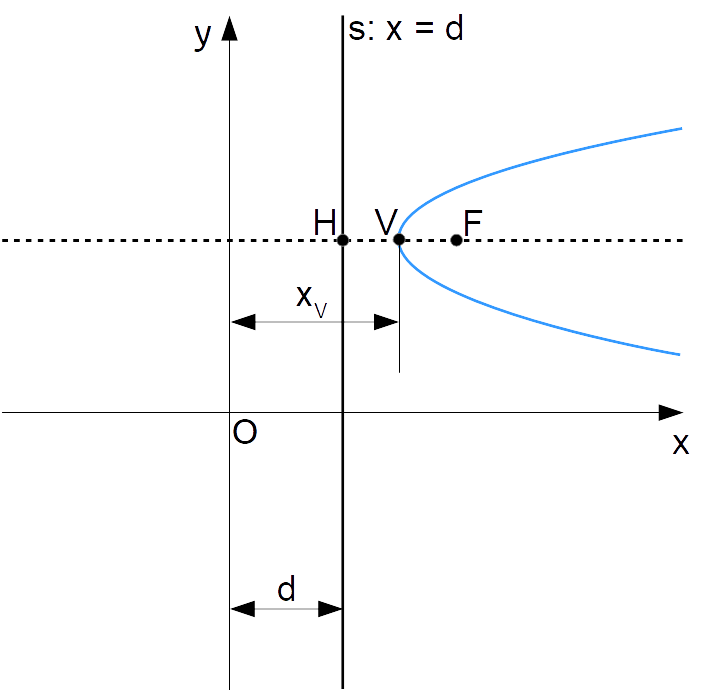
Per la definizione di parabola come luogo geometrico si ha, in modo del tutto simile al caso della parabola con asse di simmetria verticale:
\overline{FV}=\overline{VH}Osservando la figura, è immediato concludere che si ha:
d=x_V-\overline{VH}=x_V-\overline{FV}e quindi, utilizzando la definizione di lunghezza algebrica in modo da poter scrivere una relazione valida in generale:
d=x_V+\overbrace{(x_V-x_F)}^{FV} \quad \Rightarrow \quad \boxed{d=2x_V-x_F}Gli accorgimenti sui segni adottati in questo caso sono del tutto simili a quelli visti per le parabole con asse verticale.
Per una parabola con asse di simmetria orizzontale la distanza con segno {d} della direttrice rispetto all’asse delle {y} è data da:{d=2x_V-x_F}ove {x_V} è l’ascissa del vertice mentre {x_F} è l’ascissa del fuoco della parabola.
Come verifica, ricordiamo che per una parabola con asse orizzontale si ha:
x_F=\dfrac{1-\Delta}{4a}; \qquad x_V=-\dfrac{\Delta}{4a}Sostituendo tali espressioni si ha:
\begin{align*} &d=2x_V-x_F=-\dfrac{2\Delta}{4a}-\dfrac{1-\Delta}{4a}=\dfrac{-2\Delta-1+\Delta}{4a}=\\ \\ & =\dfrac{-\Delta-1}{4a}=\dfrac{-1 \cdot (\Delta+1)}{4a}=-\dfrac{1+\Delta}{4a}=d\end{align*}Abbiamo così ritrovato l’espressione della distanza con segno {d} della direttrice rispetto all’asse {y} relativa ad una parabola con asse orizzontale. La formula per {d} è dunque verificata e valida in generale.
Esempio 4
Determinare l’equazione della parabola avente fuoco {F=(-7,-3)} e vertice {V=(-4, -3)}.
Poiché il fuoco ed il vertice hanno la stessa ordinata, la parabola ha asse di simmetria orizzontale.
Cominciamo ricavando la distanza con segno {d} (attenzione ad utilizzare la formula relativa ad una parabola con asse di simmetria orizzontale):
\begin{align*} &d=2x_V-x_F=2 \cdot (-4)-(-7)=-8+7=-1\end{align*}E’ ora necessario ricordare la definizione di parabola con asse di simmetria orizzontale come luogo geometrico. In particolare, è di nostro interesse per risolvere il problema l’uguaglianza:
(x_F-x)^2+(y_F-y)^2=(x-d)^2
ovvero sostituendo i valori delle coordinate del fuoco e della distanza {d} e sviluppando i calcoli:
\begin{align*} &(-7-x)^2+(-3-y)^2=[x-(-1)]^2; \\ \\ & 49+14x+\cancel{x^2}+9+6y+y^2=\cancel{x^2}+2x+1;\\ \\ &2x-14x=y^2+6y+49+9-1;\\ \\ & -12x=y^2+6y+57;\\ \\ & x=-\dfrac{1}{12}y^2-\dfrac{1}{2}y-\dfrac{57}{12}\end{align*}Abbiamo così ottenuto l’equazione della parabola cercata.
Conclusioni
Abbiamo così visto in questa lezione come scrivere l’equazione di una parabola note le coordinate del fuoco e del vertice, utilizzando due differenti metodi. Nella prossima lezione continueremo lo studio delle condizioni per determinare l’equazione di una parabola occupandoci del caso di una parabola della quale siano note le coordinate del vertice e le coordinate di un punto appartenente alla parabola stessa (vertice e passaggio per un punto).
Un saluto a tutti voi e, come sempre, buono studio con SìMatematica!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
