Parabola con vertice e punto

 - 

Parabola (scuole superiori)

Per trovare l’equazione di una parabola con asse verticale o orizzontale con vertice e punto, occorre risolvere un sistema contenente le condizioni di appartenenza del vertice e del punto alla parabola, ed in più l’uguaglianza tra una coordinata del vertice a scelta e la corrispondente espressione in funzione dei coefficienti dell’equazione.

In alternativa, per determinare l’equazione di una parabola con asse verticale o orizzontale note le coordinate del vertice e di un punto di essa, è anche possibile ricavare le coordinate del fuoco e il valore della distanza d, e quindi scrivere l’equazione cercata sfruttando la definizione di parabola come luogo geometrico.

In questa lezione proseguiremo dunque lo studio delle condizioni per determinare l’equazione di una parabola considerando il caso di una parabola con disposizione del proprio asse nota e della quale siano date le coordinate del vertice e di un punto ad essa appartenente. Ciò significa che è possibile trovare l’equazione di una parabola con asse verticale od orizzontale conoscendo il vertice e posta la condizione di passaggio della parabola stessa per una dato punto del piano.

Come anticipato, per risolvere il problema è possibile utilizzare due differenti metodi, che illustreremo nel seguito fornendo anche degli esempi.

Equazione di una parabola con vertice e punto: metodo del sistema per ricavare i coefficienti dell’equazione

L’idea del primo metodo che analizzeremo è quella di impostare un sistema di tre equazioni in tre incognite che consenta di ricavare i valori dei tre coefficienti dell’equazione della parabola. Noti infatti tali valori, conoscendo la disposizione dell’asse della parabola sarà immediato scriverne l’equazione.

Consideriamo una parabola con asse di simmetria verticale, e quindi con equazione:

y=ax^2+bx+c, \qquad a \neq 0, \quad a,b,c \in \R

Supponiamo di conoscere le coordinate del vertice della parabola e le coordinate di un punto appartenente alla parabola stessa:

V=(x_V, y_V); \qquad P=(x_P, y_P)

Come il punto {P}, anche il vertice è un punto che appartiene alla parabola. Di conseguenza, entrambi i punti devono soddisfare la relativa condizione di appartenenza alla parabola. In particolare, per le coordinate del vertice {V} dovrà risultare verificata l’uguaglianza:

y_V=ax_V^2+bx_V+c

mentre per le coordinate del punto {P} dovrà essere in modo del tutto simile:

y_P=ax_P^2+bx_P+c

Ora, per poter scrivere l’equazione della parabola occorrono i valori di tutti e tre i coefficienti {a,b,c}. Ma per il momento abbiamo due sole condizioni, date dalle condizioni di appartenenza di {V} e {P} alla parabola.

Tuttavia, è immediato ottenere una terza condizione ricordando che per una parabola con asse di simmetria verticale l’ascissa del vertice è data da {-\dfrac{b}{2a}}.

Di conseguenza, poiché conosciamo l’ascissa del vertice, possiamo scrivere l’uguaglianza:

-\dfrac{b}{2a}=x_V

Ora disponiamo della terza condizione che mancava, e possiamo impostare il sistema seguente:

\begin{cases} -\dfrac{b}{2a}=x_V \\ \\ y_V=ax_V^2+bx_V+c \\ \\y_P=ax_P^2+bx_P+c  \end{cases}

Osserviamo che per la condizione relativa alla prima equazione a sistema abbiamo scelto di utilizzare l’espressione dell’ascissa del vertice e non dell’ordinata. Infatti, come si ricorderà dalle precedenti lezioni, l’espressione dell’ordinata del vertice dipende da {\Delta=b^2-4ac}, e quindi in tale espressione figura una variabile di secondo grado. Di conseguenza, se utilizzassimo l’espressione dell’ordinata del vertice per scrivere la prima equazione del sistema non ci ritroveremmo sicuramente con un sistema lineare.

Invece, con la scelta operata è immediato ritrovarci con un sistema lineare. Infatti, per {a\neq 0} possiamo ricondurre la prima equazione a sistema alla forma intera:

\begin{cases} b=-2a x_V, \qquad a \neq 0\\ \\ y_V=ax_V^2+bx_V+c \\ \\y_P=ax_P^2+bx_P+c  \end{cases}

La condizione {a \neq 0} non è restrittiva ed è certamente soddisfatta poiché nell’equazione di una parabola con asse verticale od orizzontale il coefficiente {a} è sempre diverso da zero.

Per meglio evidenziare le incognite, è utile riscrivere il sistema come segue:

\begin{cases}b=-2x_Va\\ \\ x_V^2a+x_Vb+c=y_V \\ \\x_P^2a+x_Pb+c= y_P \end{cases} \quad \small \text{parabola con asse } \textbf{verticale}

Per risolvere il sistema basta sostituire nelle equazioni che figurano in esso i valori delle coordinate del vertice {V} e del punto {P} della parabola, e quindi utilizzare uno dei metodi a noi conosciuti per risolvere un sistema lineare di tre equazioni in tre incognite. Come vedremo negli esempi, in questo caso risulta particolarmente comodo il metodo di sostituzione.

Con ragionamenti del tutto simili, il sistema da utilizzare nel caso di una parabola con asse di simmetria orizzontale è:

\begin{cases}b=-2y_Va\\ \\ y_V^2a+y_Vb+c=x_V \\ \\y_P^2a+y_Pb+c= x_P \end{cases} \quad  \small \text{parabola con asse } \textbf{orizzontale}

Vediamo subito degli esempi relativi a ciascun caso.

Esempio 1

Scrivere l’equazione della parabola con asse verticale passante per il punto {P=(-2,5)} e con vertice {V=(1,2)}.

Poiché il testo afferma che la parabola ha asse di simmetria verticale, questa avrà equazione della forma:

y=ax^2+bx+c, \qquad a\neq0 , \quad a,b,c \in \R

Per poter scrivere l’equazione dobbiamo ricavare i valori dei coefficienti {a,b,c} corrispondenti al caso in esame.

Il sistema da risolvere è il seguente:

\begin{cases}b=-2x_Va\\ \\ x_V^2a+x_Vb+c=y_V \\ \\x_P^2a+x_Pb+c= y_P \end{cases} 

ovvero, sostituendo i valori delle coordinate del punto {P} e del vertice:

\begin{cases} b=-2 \cdot 1\cdot a \\ \\ 1^2 \cdot a + 1 \cdot b+c=2 \\ \\ (-2)^2\cdot a + (-2) \cdot b+c=5\end{cases}

Abbiamo così il sistema:

\begin{cases} b=-2a \\ \\ a+b+c=2 \\ \\ 4a-2b+c=5\end{cases}

Se intendiamo risolvere il sistema utilizzando il metodo di sostituzione o il metodo di Cramer, dobbiamo riscriverlo in forma normale. Per fare ciò, nel nostro caso dobbiamo riesprimere la prima equazione come segue:

\begin{cases} 2a+b+0 \cdot c=0 \\ \\ a+b+c=2 \\ \\ 4a-2b+c=5\end{cases}

Osserviamo che abbiamo anche provveduto ad evidenziare nella prima equazione il termine in {c} con coefficiente {0}: ciò serve per evitare errori nell’applicazione della regola di Cramer.

Tuttavia, a nostro parere per risolvere il sistema conviene procedere per sostituzione. Riconsideriamo il sistema nella forma:

\begin{cases} b=-2a \\ \\ a+b+c=2 \\ \\ 4a-2b+c=5\end{cases}

La prima equazione fornisce già un’espressione per {b} che possiamo sostituire nella seconda e terza equazione:

\begin{cases} b=-2a \\ \\ a-2a+c=2 \\ \\ 4a-2\cdot(-2a)+c=5\end{cases} \quad \Rightarrow \quad \begin{cases} b=-2a \\ \\ -a+c=2 \\ \\ 8a+c=5\end{cases}

Mettiamo da parte per il momento la prima equazione. Ci ritroviamo in questo modo, temporaneamente, con un sistema di due equazioni in due incognite:

 \begin{cases} \dots \\ \\ -a+c=2 \\ \\ 8a+c=5\end{cases}

Procedendo per sostituzione abbiamo:

\begin{cases} \dots \\ \\ -a+c=2 \quad \rightarrow c=2+a \\ \\ 8a+c=5 \quad \rightarrow \quad 8a+2+a=5 \quad \rightarrow \: 9a=3 \quad \rightarrow \: a=\dfrac{1}{3}\end{cases}

e quindi per {c}:

\begin{cases} \dots \\ \\ c=2+\dfrac{1}{3} \quad \rightarrow \quad c=\dfrac{7}{3} \\ \\ a=\dfrac{1}{3}\end{cases}

A questo punto riprendiamo la prima equazione, in modo da ricavare il valore del coefficiente {b}:

\begin{cases} b=-2a \quad \rightarrow b=-2 \cdot \dfrac{1}3{ \quad \rightarrow \quad b=-\dfrac{2}{3}}\\ \\ c=\dfrac{7}{3} \\ \\ a=\dfrac{1}{3}\end{cases}

Ora disponiamo dei valori di tutti e tre i coefficienti {a,b,c} e possiamo in conclusione scrivere l’equazione della parabola in esame (ricordiamo che la parabola ha asse verticale):

y=\dfrac{1}{3}x^2-\dfrac{2}{3}x+\dfrac{7}{3}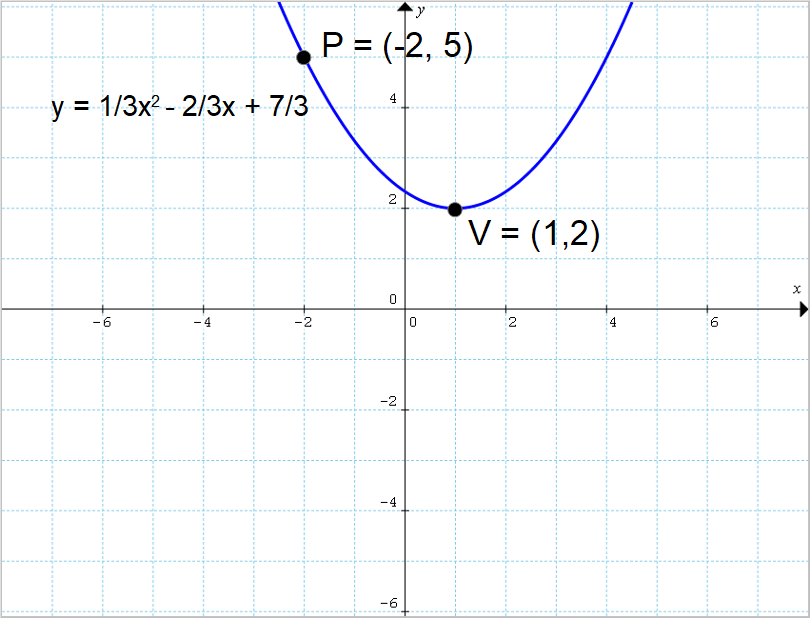

Vediamo ora un esempio relativo al caso di una parabola con asse orizzontale.

Esempio 2

Determinare l’equazione della parabola con asse di simmetria orizzontale avente vertice {V=(-2,7)} e passante per il punto {P=(-1,4)}.

Poiché la parabola ha asse di simmetria orizzontale, il sistema da utilizzare è il seguente:

\begin{cases}b=-2y_Va\\ \\ y_V^2a+y_Vb+c=x_V \\ \\y_P^2a+y_Pb+c= x_P \end{cases} 

Attenzione a non utilizzare per errore il sistema relativo al caso di una parabola con asse verticale.

Sostituendo i valori delle coordinate del vertice e del punto {P} nelle equazioni a sistema otteniamo:

\begin{cases} b=-14a \\ \\ 49a+7b+c=-2 \\ \\ 16a+4b+c=-1\end{cases}

Risolviamo il sistema per sostituzione:

\small \begin{cases} b=-14a \\ \\ 49a+7\cdot(-14a)+c=-2 \quad \rightarrow \: 49a-98a+c=-2 \quad \rightarrow \: c=49a-2 \\ \\ 16a+4\cdot (-14a)+c=-1 \quad \rightarrow \: 16a-56a+49a-2=-1 \quad \rightarrow \: a=\dfrac{1}{9}\end{cases}

e quindi:

\begin{cases}b=-14 \cdot\dfrac{1}{9}=-\dfrac{14}{9} \\ \\ c=49 \cdot \dfrac{1}{9}-2 \quad \rightarrow \quad c=\dfrac{31}{9}\\ \\ a = \dfrac{1}{9}\end{cases}

Così in conclusione ai valori ottenuti per {a,b,c} corrisponde per la parabola data l’equazione (ricordiamo che la parabola ha asse orizzontale):

x=\dfrac{1}{9}y^2-\dfrac{14}{9}y+\dfrac{31}{9}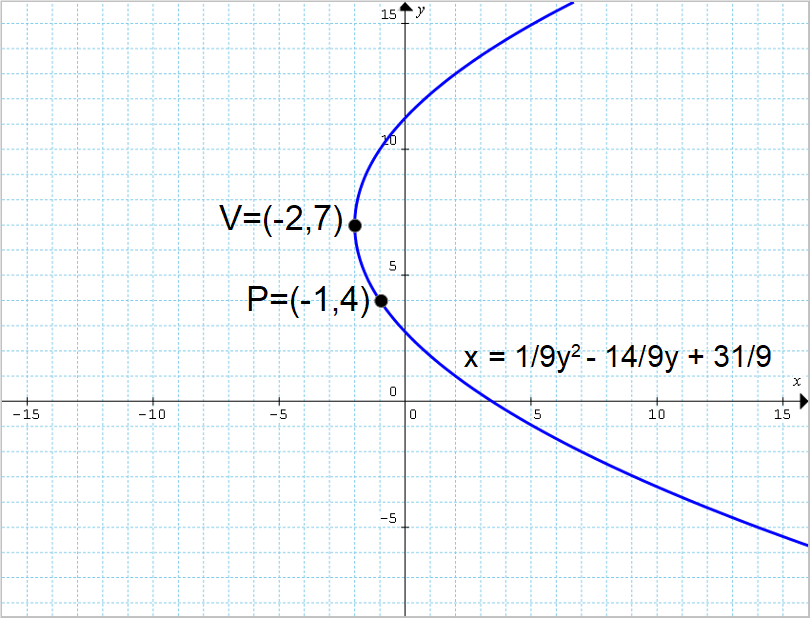

Parabola con vertice e punto: metodo del ricavare le coordinate del fuoco e la distanza con segno d

In alternativa al metodo sin qui visto, è possibile determinare l’equazione di una parabola a partire dalle coordinate del vertice e di un suo punto ricavando le coordinate del fuoco e la distanza con segno {\boldsymbol{d}}.

Metodo delle coordinate del fuoco e della distanza d: parabola con asse verticale

Consideriamo una parabola con asse di simmetria verticale, avente equazione:

y=ax^2+bx+c, \qquad a \neq 0, \quad a,b,c \in \R

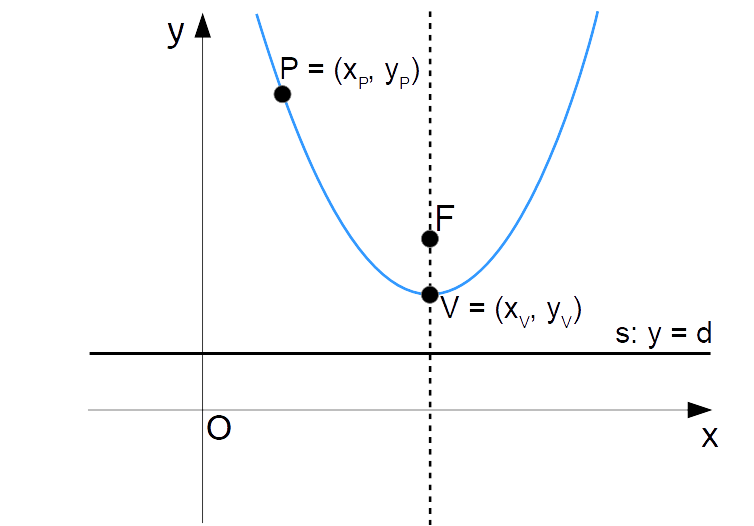
I dati di partenza sono le coordinate del vertice {V} e le coordinate del punto {P}. Il nostro obiettivo è ricavare le coordinate del fuoco e la distanza con segno {d}, in modo da poter scrivere l’equazione della parabola.

Per la definizione di parabola con asse verticale come luogo geometrico, deve intanto valere l’uguaglianza:

(x_F-x_P)^2+(y_F-y_P)^2=(y_P-d)^2

In altre parole, il quadrato della distanza tra i punti {F} e {P} (primo membro) deve esse uguale al quadrato della distanza tra il punto {P} e la direttrice (secondo membro). Ciò rispecchia la definizione di parabola come luogo geometrico: un qualunque punto {P} appartenente alla parabola deve avere la stessa distanza dal fuoco e dalla direttrice.

Osserviamo che nell’equazione abbiamo tre incognite: le coordinate {x_F} e {y_F} del fuoco e la distanza con segno {d} della direttrice rispetto all’asse {x}. Tuttavia, per quanto visto nella precedente lezione si ha:

d=2y_V-y_F

Così, sostituendo l’espressione appena scritta per {d} nel secondo membro della precedente equazione abbiamo:

(x_F-x_P)^2+(y_F-y_P)^2=(y_P-2y_V+y_F)^2

Inoltre, è immediato ricavare il valore dell’ascissa del fuoco. Come è evidente dalla precedente figura, questa è infatti uguale all’ascissa del vertice. Così possiamo scrivere:

\boxed{(x_V-x_P)^2+(y_F-y_P)^2=(y_P-2y_V+y_F)^2}

Ora l’equazione è nella sola incognita {y_F}. Così, sostituendo i valori delle coordinate di {V} e {P}, eseguendo i calcoli e riordinando i termini è possibile ottenere un’equazione nella sola variabile {y_F}. Quindi, risolvendo l’equazione otteniamo l’ordinata del fuoco. E a tal punto, riprendendo la relazione {d=2y_V-y_F} sarà possibile calcolare il valore della distanza con segno {d}.

Di conseguenza, note a questo punto le coordinate del fuoco e la distanza {d}, potremo determinare l’equazione della parabola sfruttando la definizione come luogo geometrico relativa ad una generico punto della parabola:

(x_F-x)^2+(y_F-y)^2=(y-d)^2

Vediamo subito un esempio.

Esempio 3

Determinare l’equazione della parabola con asse verticale avente vertice {V=(-3, - 5)} e passante per il punto {P=(2,1)}.

Partiamo direttamente dall’uguaglianza:

(x_V-x_P)^2+(y_F-y_P)^2=(y_P-2y_V+y_F)^2

uguaglianza che possiamo ricavare con non troppa difficoltà utilizzando i ragionamenti visti in precedenza.

Attenzione: prima di calcolare i quadrati dobbiamo sostituire i valori delle coordinate a noi noti. Si ha:

(-3-2)^2+(y_F-1)^2=[1-2 \cdot (-5)+y_F]^2

Ora possiamo calcolare i quadrati e riordinare i termini:

\begin{align*} &(-5)^2+y_F^2-2y_F+1=(11+y_F)^2;\\ \\ & 25+\cancel{y_F^2}-2y_F+1=121+22y_F+\cancel{y_F^2};\\ \\ & 24y_F=25+1-121;\\ \\ & 24y_F=-95 \quad \Rightarrow \quad y_F=-\dfrac{95}{24}\end{align*}

Ora ricaviamo la distanza con segno {d}:

\begin{align*} & d=2y_V-y_F=2 \cdot (-5)-\left( -\dfrac{95}{24}\right)=-10+\dfrac{95}{24}=\dfrac{-240+95}{24}=\\ \\ & =-\dfrac{145}{24} \end{align*}

Infine, sfruttando la definizione di parabola come luogo geometrico relativamente al generico punto della parabola:

(x_F-x)^2+(y_F-y)^2=(y-d)^2

e quindi sostituendo i valori ormai noti (ricordiamo che in una parabola con asse verticale l’ascissa del fuoco è uguale all’ascissa del vertice):

(-3-x)^2+\left( -\dfrac{95}{24}-y\right)^2=\left[ y-\left( -\dfrac{145}{24}\right)\right]^2

e quindi:

(-3-x)^2+\left( -\dfrac{95}{24}-y\right)^2=\left( y+\dfrac{145}{24}\right)^2

Svolgendo i calcoli (in questo caso un po’ scomodi a causa dei valori di partenza forniti dal problema):

\begin{align*} &9+6x+x^2+\dfrac{95^2}{24^2}+\dfrac{95}{12}y+\cancel{y^2}=\cancel{y^2}+\dfrac{145}{12}y+\dfrac{145^2}{24^2};\\ \\ &\left( -\dfrac{145}{12}+\dfrac{95}{12}\right)y+x^2+6x=\dfrac{145^2}{24^2}-9-\dfrac{95^2}{24^2} ;\\ \\ & \dfrac{25}{6}y=x^2+6x-\dfrac{145^2}{24^2}+9+\dfrac{95^2}{24^2};\\ \\ & y=\dfrac{6}{25}x^2+\dfrac{36}{25}x+\dfrac{\cancel{6}}{25}\cdot\left( \dfrac{-145^2+9\cdot24^2+95^2}{6^{\cancel{2}} \cdot 4^2}\right) \\ \\ &y=\dfrac{6}{25}x^2+\dfrac{36}{25}x+\dfrac{1}{25}\cdot\dfrac{-145^2+9\cdot24^2+95^2}{96} \\ \\ & y= \dfrac{6}{25}x^2+\dfrac{36}{25}x-\dfrac{71}{25}\end{align*}

Quindi, quella appena scritta è l’equazione della parabola relativa al caso in esame.

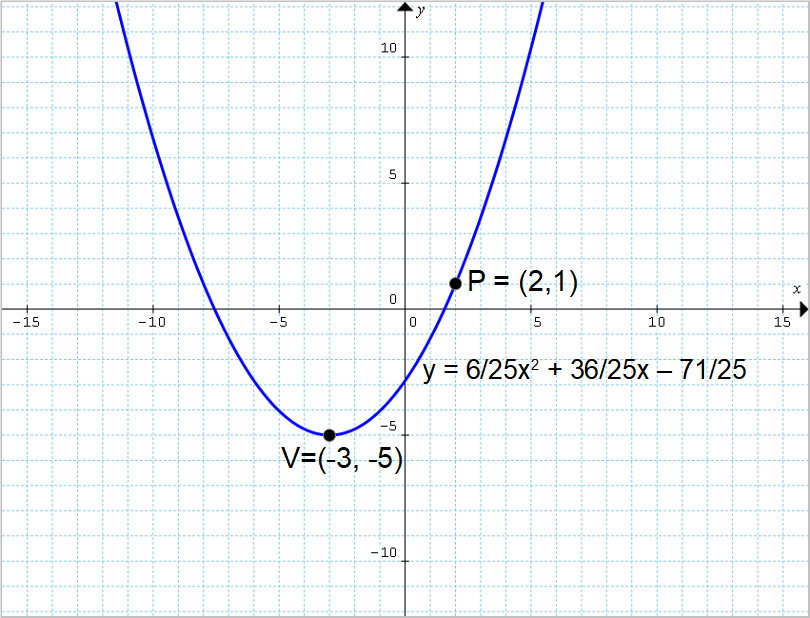
Metodo delle coordinate del fuoco e della distanza d: parabola con asse orizzontale

Consideriamo una parabola con asse di simmetria orizzontale, e quindi una parabola avente equazione:

x=ay^2+by+c, \qquad a \neq 0 , \quad a,b,c \in \R

Il nostro obiettivo è anche in questo caso ricavare i coefficienti {a,b,c} a partire dalle coordinate del vertice {V} e del punto {P}.

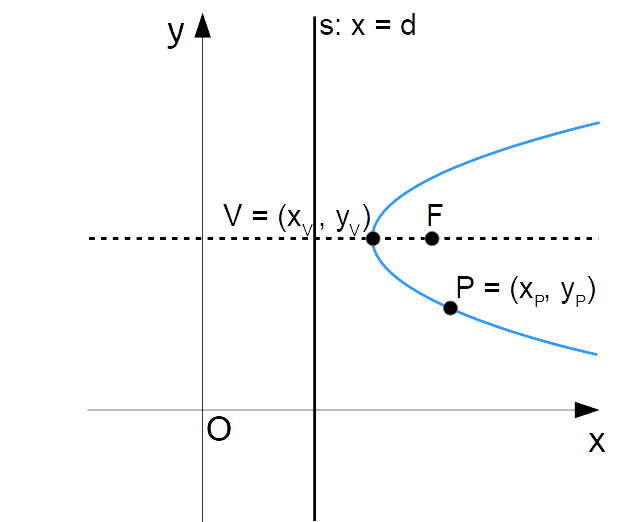
Dalla definizione di parabola con asse orizzontale come luogo geometrico si ha:

(x_F-x_P)^2+(y_F-y_P)^2=(x_P-d)^2 

Ricordiamo che per una parabola con asse orizzontale si ha (vedi lezione precedente):

d=2x_V-x_F

Inoltre, l’ordinata del fuoco e l’ordinata del vertice coincidono. Di conseguenza, la precedente uguaglianza relativa alla definizione di parabola con asse orizzontale come luogo geometrico diviene:

(x_F-x_P)^2+(y_V-y_P)^2=(x_P-2x_V+x_F)^2

Sostituendo nell’uguaglianza appena scritta i valori delle coordinate del vertice {V} e del punto {P} otteniamo un’equazione nella sola variabile {x_F}. Di conseguenza, risolvendo tale equazione è possibile ricavare il valore dell’ordinata del fuoco.

Una volta noto il valore di {x_F}, si procede calcolando il valore di {d}, mediante la formula {d=2x_V-x_F}.

Così, disponendo delle coordinate del fuoco e della distanza {d} possiamo infine determinare l’equazione della parabola, sfruttando ancora la definizione di parabola con asse orizzontale come luogo geometrico, relativa stavolta ad un generico punto della parabola di coordinate {x} ed {y}:

(x_F-x)^2+(y_F-y)^2=(x-d)^2

Osserviamo ancora che l’ordinata del fuoco {y_F} è uguale all’ordinata del vertice {y_V}, che è nota. Quindi anche il valore di {y_F} è noto.

Sostituendo quindi i valori delle coordinate del fuoco e della distanza {d}, calcolando i quadrati ed infine riordinando i termini perveniamo in conclusione all’equazione cercata.

Esempio 4

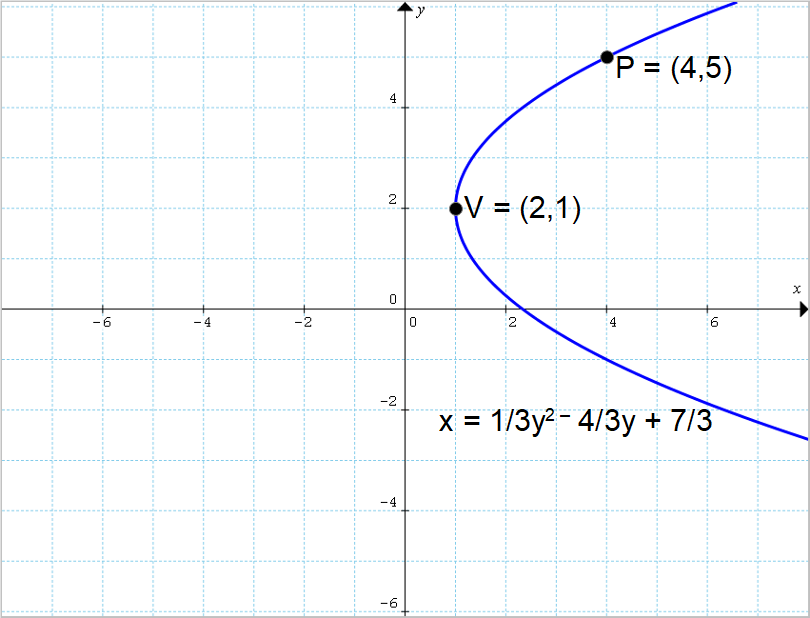
Scrivere l’equazione della parabola con asse orizzontale avente vertice {V=(1,2)} e passante per il punto {P=(4,5)}.

Consideriamo l’equazione, che possiamo ricavare seguendo i ragionamenti fatti in precedenza:

(x_F-x_P)^2+(y_V-y_P)^2=(x_P-2x_V+x_F)^2

Sostituiamo prima di tutto in essa i valori delle coordinate noti, quindi risolviamola:

\begin{align*} & (x_F-4)^2+(2-5)^2=(4-2 \cdot 1 + x_F)^2; \\ \\ & \cancel{x_F^2}-8x_F+16+9=4+4x_F+\cancel{x_F^2}; \\ \\ & 12x_F=16+9-4;\\ \\ & 12x_F=21 \quad \Rightarrow \quad x_F=\dfrac{21}{12}=\dfrac{7}{4}\end{align*}

Ottenuto il valore di {x_F}, calcoliamo {d}:

d=2x_V-x_F=2\cdot1-\dfrac{7}{4}=\dfrac{8-7}{4}=\dfrac{1}{4}

Ora possiamo determinare l’equazione della parabola a partire dalla sua definizione come luogo geometrico:

(x_F-x)^2+(y_F-y)^2=(x-d)^2

Osserviamo che entrambe le coordinate del fuoco sono note. Infatti, abbiamo calcolato il valore di {x_F} nei passaggi precedenti, ed inoltre il valore di {y_F} è uguale al valore di {y_V}, che è noto. Così sostituendo i valori si ha:

\begin{align*} &\left( \dfrac{7}{4}-x\right)^2+(2-y)^2=\left(x- \dfrac{1}{4}\right)^2; \\ \\ & \dfrac{49}{16}-\dfrac{7}{2}x+\cancel{x^2}+4-4y+y^2=\cancel{x^2}-\dfrac{1}{2}x+\dfrac{1}{16};\\ \\ & \left( -\dfrac{1}{2}+\dfrac{7}{2}\right)x=y^2-4y+4+\dfrac{49}{16}-\dfrac{1}{16};\\ \\ & 3x=y^2-4y+\dfrac{112}{16};\\ \\ & x=\dfrac{1}{3}y^2-\dfrac{4}{3}y+\dfrac{7}{3}\end{align*}

Abbiamo quindi ottenuto l’equazione della parabola cercata.

Per quanto riguarda come determinare l’equazione di una parabola con asse verticale o orizzontale a partire dalle coordinate del vertice e di un suo punto è tutto. Nella prossima lezione continueremo ad analizzare le condizioni per individuare univocamente una parabola nel piano, considerando il caso di una parabola della quale si conoscono le coordinate del vertice e l’equazione della direttrice.

Un saluto e buono studio con SìMatematica!