Parabola con vertice e direttrice

 - 

Parabola (scuole superiori)

Per trovare l’equazione di una parabola con asse verticale od orizzontale date le coordinate del vertice e l’equazione della direttrice, è possibile impostare un sistema utilizzando le espressioni delle coordinate del vertice e dell’equazione della direttrice in funzione dei coefficienti a, b, c dell’equazione della parabola. Risolvendo il sistema sarà possibile ottenere i valori di tali coefficienti e quindi scrivere l’equazione della parabola.

In alternativa, è anche possibile calcolare la coordinata mancante del fuoco, e quindi scrivere l’equazione della parabola a partire dalla definizione di parabola come luogo geometrico.

Così, proseguiamo il nostro studio sulle condizioni per determinare l’equazione di una parabola considerando il caso di una parabola con asse verticale od orizzontale della quale conosciamo le coordinate del vertice e l’equazione della direttrice. In particolare, illustreremo nel dettaglio entrambi i metodi utilizzabili, occupandoci della teoria e fornendo degli esercizi di esempio. Come vedremo, uno dei due metodi utilizza delle formule che si possono ottenere ribaltando opportunamente le formule date a suo tempo per il caso di una parabola con fuoco e vertice noti. Vedremo comunque come ottenere tali formule anche occupandoci soltanto del caso specifico oggetto della presente lezione.

Parabola con vertice e direttrice: metodo del sistema

Vediamo il metodo che si basa nell’impostare un opportuno sistema di tre equazioni in tre incognite, grazie al quale è possibile ricavare i valori dei coefficienti {a,b,c} necessari per scrivere l’equazione della parabola in esame. Ci occuperemo dei due distinti casi di una parabola con asse verticale e di una parabola con asse orizzontale.

Metodo del sistema per trovare l’equazione di una parabola con asse verticale noti vertice e direttrice

Consideriamo una parabola con asse di simmetria verticale, ovvero una parabola di equazione in forma generale:

y=ax^2+bx+c, \qquad a\neq0, \quad a,b,c \in \R

Sono note le coordinate del vertice e l’equazione della direttrice:

V=(x_V, y_V), \qquad s:y=d

In altre parole sono noti i valori {x_V, y_V} e {d}.

Il nostro obiettivo è determinare i valori dei coefficienti {a,b,c}, in modo da poter scrivere l’equazione della parabola in esame.

Ricordiamo che per una parabola con asse di simmetria verticale le coordinate del vertice sono esprimibili come:

\boxed{x_V=-\dfrac{b}{2a}}; \qquad \boxed{y_V=-\dfrac{\Delta}{4a}}

Inoltre, l’equazione della direttrice è data da:

y=-\dfrac{1+\Delta}{4a}

da cui:

\boxed{d=-\dfrac{1+\Delta}{4a}}

Mettendo a sistema tutte le uguaglianze evidenziate nei riquadri abbiamo:

\begin{cases} x_V=-\dfrac{b}{2a} \\ \\ y_V=-\dfrac{\Delta}{4a} \\ \\d=-\dfrac{1+\Delta}{4a}  \end{cases}

ovvero, riordinando i termini e ricordando che {\Delta = b^2-4ac}:

\begin{cases} -\dfrac{b}{2a}=x_V \\ \\ \dfrac{4ac-b^2}{4a}=y_V \\ \\ \dfrac{4ac-1-b^2}{4a}=d\end{cases} \qquad \small \text{parabola con asse verticale}

Osserviamo che nella seconda e nella terza equazione abbiamo lavorato opportunamente sui segni al numeratore del primo membro.

Il sistema da risolvere è del tipo non lineare, tuttavia per risolverlo basta utilizzare, come nei casi delle lezioni precedenti, il metodo di sostituzione. Una volta risolto il sistema, disporremo dei valori dei coefficienti {a,b,c} che permettono di scrivere l’equazione della parabola in esame.

Esempio 1

Determinare l’equazione della parabola avente vertice {V=(1,2)} e direttrice di equazione {s:y=-5}.

Osserviamo che la direttrice è una retta orizzontale. Infatti, questa è formata da punti aventi tutti la stessa ordinata. Ora, l’asse di una parabola è sempre perpendicolare alla direttrice. Così, dato che nel nostro caso la direttrice è orizzontale, l’asse della parabola sarà necessariamente verticale. Di conseguenza, ci ritroviamo nel caso di una parabola con asse di simmetria verticale.

Per risolvere il problema, dobbiamo impostare il seguente sistema:

\begin{cases} -\dfrac{b}{2a}=x_V \\ \\ \dfrac{4ac-b^2}{4a}=y_V \\ \\ \dfrac{4ac-1-b^2}{4a}=d\end{cases}

Per poter risolvere il sistema rispetto alle incognite {a,b,c}, dobbiamo prima di tutto sostituire i valori ai secondi membri delle equazioni a sistema.

Le coordinate del vertice sono fornite direttamente dal testo. Per la distanza con segno {d} della direttrice rispetto all’asse {x} si ha:

d=-5

Questa infatti corrisponde al secondo membro dell’equazione della direttrice.

Sostituendo i valori dei secondi membri delle equazioni a sistema abbiamo:

\begin{cases} -\dfrac{b}{2a}=1 \\ \\ \dfrac{4ac-b^2}{4a}=2 \\ \\ \dfrac{4ac-1-b^2}{4a}=-5\end{cases}

Per risolvere il sistema, cominciamo ricavando un’espressione per {b} dalla prima equazione (la condizione {a \neq 0} è sicuramente rispettata, poiché come sappiamo per avere l’equazione di una parabola deve essere necessariamente {a \neq 0}).

\begin{cases} -\dfrac{b}{2a}=1 \quad \rightarrow \quad b=-2a \\ \\ \dfrac{4ac-b^2}{4a}=2 \\ \\ \dfrac{4ac-1-b^2}{4a}=-5\end{cases}

Ora sostituiamo l’espressione appena ottenuta per {b} nella seconda e nella terza equazione:

\begin{cases}  b=-2a \\ \\ \dfrac{4ac-(-2a)^2}{4a}=2 \\ \\ \dfrac{4ac-1-(-2a)^2}{4a}=-5\end{cases} \quad \Rightarrow \quad \begin{cases} b=-2a \\ \\ \dfrac{\cancel{4a}(c-a)}{\cancel{4a}}=2 \\ \\ \dfrac{4ac-1-4a^2}{4a}=-5\end{cases}

Abbiamo:

\begin{cases} b=-2a \\ \\c-a=2 \quad \rightarrow \quad c=2+a \\ \\ \dfrac{4ac-1-4a^2}{4a}=-5\end{cases}

e quindi sostituendo l’espressione appena ottenuta per {c} nella terza equazione:

\small\begin{cases} b=-2a \\ \\c=2+a \\ \\ \dfrac{4a(2+a)-1-4a^2}{4a}=-5 \quad \rightarrow \: \dfrac{8a+\cancel{4a^2}-1-\cancel{4a^2}+20a}{\cancel{4a}}=0 \quad \rightarrow \: a=\dfrac{1}{28}\end{cases}

Sostituendo infine il valore appena ottenuto per {a} nelle rimanenti equazioni:

\begin{cases} b=-2 \cdot \dfrac{1}{28} \quad \rightarrow \: b=-\dfrac{1}{14} \\ \\ c=2+a \quad \rightarrow \: c=2+\dfrac{1}{28} \quad \rightarrow c=\dfrac{57}{28} \\ \\ a=\dfrac{1}{28} \end{cases}

Ricordiamo che la parabola in esame ha asse verticale, ed ha quindi equazione della forma generale:

y=ax^2+bx+c

Così sostituendo i valori dei coefficienti {a,b, c} possiamo in conclusione scrivere l’equazione della parabola in esame:

y=\dfrac{1}{28}x^2-\dfrac{1}{14}x+\dfrac{57}{28}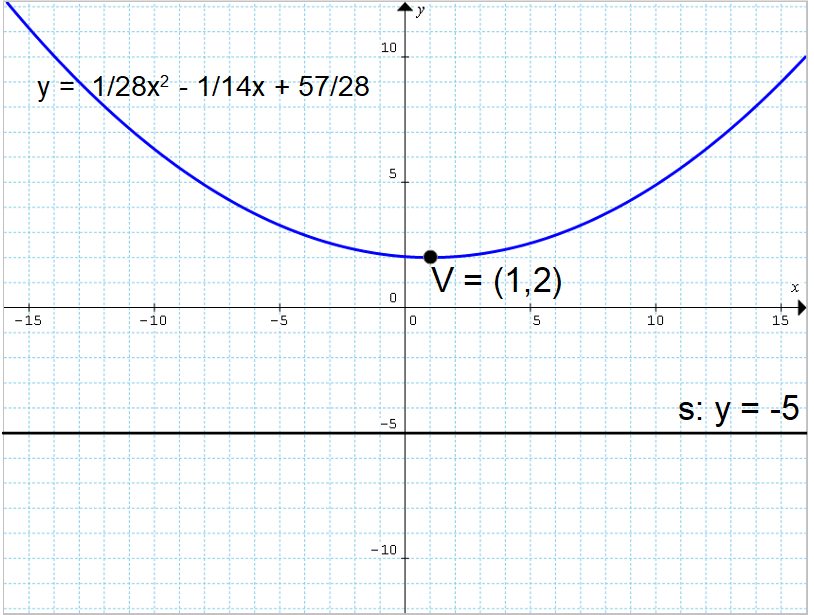

Metodo del sistema per trovare l’equazione di una parabola con asse orizzontale noti vertice e direttrice

Vediamo ora come applicare il metodo al caso di una parabola con asse orizzontale, ovvero di una parabola con equazione in forma generale:

x=ay^2+by+c, \qquad a \neq0, \quad a,b,c \in \R

I dati in nostro possesso sono ancora le coordinate del vertice e l’equazione della direttrice:

V=(x_V, y_V); \qquad s:x=d

L’obiettivo rimane quello di ricavare i valori dei coefficienti {a,b,c}, in modo da poter scrivere l’equazione relativa alla parabola in esame.

Ricordiamo che per una parabola con asse orizzontale si ha:

x_V=-\dfrac{\Delta}{4a}; \qquad y_V=-\dfrac{b}{2a}; \qquad d=-\dfrac{1+\Delta}{4a}

Poiché tali uguaglianze devono valere contemporaneamente, queste possono essere messe a sistema. Ricordando che {\Delta=b^2-4ac} e riordinando i termini si ha:

\begin{cases} -\dfrac{b}{2a}=y_V \\ \\ \dfrac{4ac-b^2}{4a}=x_V  \\ \\ \dfrac{4ac-1-b^2}{4a}=d\end{cases} \quad \small \text{parabola con asse orizzontale}

Osserviamo che il sistema è molto simile a quello scritto per una parabola con asse verticale, con la differenza che le quantità {y_V} ed {x_V} risultano scambiate tra loro.

Risolvendo il sistema per sostituzione, allo stesso modo visto nell’esempio precedente, è possibile determinare i valori dei coefficienti {a,b,c} e quindi scrivere l’equazione della parabola data.

Esempio 2

Determinare l’equazione della parabola avente vertice {V=(-2,-3)} e direttrice di equazione {x=1}.

Poiché la direttrice è una retta verticale, la parabola ha asse di simmetria orizzontale (ricordiamo ancora che la direttrice e l’asse di simmetria di una parabola sono tra loro perpendicolari).

Scriviamo il sistema (attenzione ad utilizzare il sistema relativo ad una parabola con asse orizzontale):

\begin{cases} -\dfrac{b}{2a}=y_V \\ \\ \dfrac{4ac-b^2}{4a}=x_V  \\ \\ \dfrac{4ac-1-b^2}{4a}=d\end{cases}

Sostituiamo i valori ai secondi membri:

\begin{cases} -\dfrac{b}{2a}=-3 \\ \\ \dfrac{4ac-b^2}{4a}=-2  \\ \\ \dfrac{4ac-1-b^2}{4a}=1\end{cases}

Procediamo come fatto in precedenza risolvendo per sostituzione. Prima di tutto, esplicitiamo l’incognita {b} dalla prima equazione (ricordiamo che è valida la condizione {a \neq 0}). Quindi, sostituiamo l’espressione ottenuta per {b} nella seconda e nella terza equazione:

\begin{cases} -\dfrac{b}{2a}=-3 \quad \rightarrow \quad b=6a \\ \\ \dfrac{4ac-(6a)^2}{4a}=-2  \\ \\ \dfrac{4ac-1-(6a)^2}{4a}=1\end{cases}

Abbiamo:

\begin{cases}  b=6a \\ \\ \dfrac{4ac-36a^2}{4a}=-2 \quad \rightarrow \quad \dfrac{\cancel{4a}(c-9a)}{\cancel{4a}}=-2 \quad \rightarrow \quad c=9a-2  \\ \\ \dfrac{4ac-1-36a^2}{4a}=1\end{cases}

Sostituiamo a questo punto l’espressione ottenuta per {c} nella terza equazione, in modo da ricavare il valore di {a}:

\small\begin{cases}  b=6a \\ \\  c=9a-2  \\ \\ \dfrac{4ac-1-36a^2}{4a}=1 \quad \rightarrow \: 4a(9a-2)-36a^2-1-4a=0 \quad \rightarrow \: a=-\dfrac{1}{12}\end{cases}

Ora non resta che ricavare i valori delle incognite {b} e {c}:

\small\begin{cases}  b=6a \quad \rightarrow \quad b=6 \cdot \left( -\dfrac{1}{12}\right) \quad \rightarrow \quad b=-\dfrac{1}{2} \\ \\  c=9a-2 \quad \rightarrow \quad c=9\cdot\left( -\dfrac{1}{12}\right)-2 \quad \rightarrow \quad c=-\dfrac{11}{4}  \\ \\ a=-\dfrac{1}{12}\end{cases}

Ora, la parabola in esame ha asse di simmetria orizzontale e quindi equazione della forma generale:

x=ay^2+by+c, \qquad a \neq 0, \quad a,b,c \in \R

Sostituendo i valori dei coefficienti {a,b,c} otteniamo in conclusione l’equazione della parabola data:

x=-\dfrac{1}{12}y^2-\dfrac{1}{2}y-\dfrac{11}{4}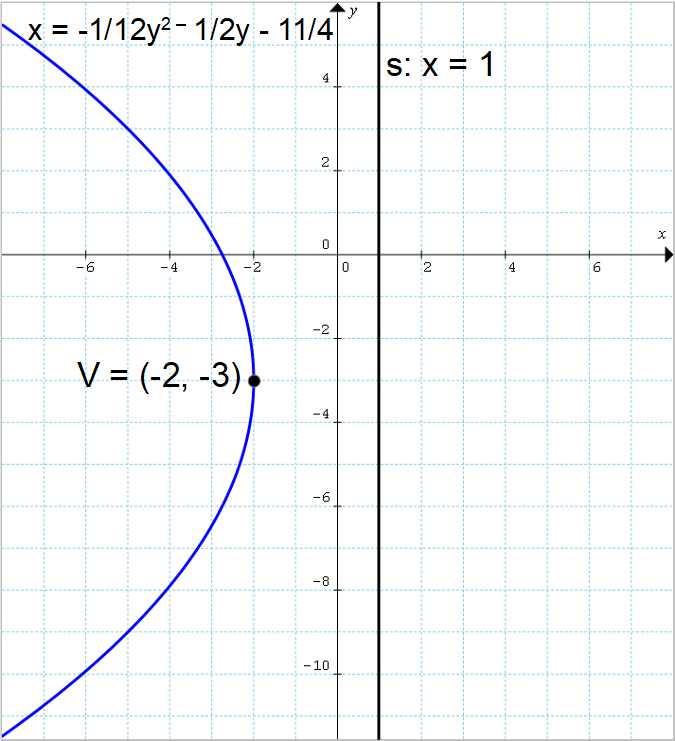

Metodo della definizione come luogo geometrico

Consideriamo ancora una parabola della quale siano note le coordinate del vertice e l’equazione della direttrice. Il nostro problema rimane quello di determinare l’equazione della parabola.

In alternativa al metodo sin qui visto è possibile ricercare la coordinata mancante del fuoco e quindi scrivere l’equazione della parabola sfruttando la sua definizione come luogo geometrico.

Vediamo come procedere in entrambi i casi di parabola con asse verticale ed orizzontale.

Metodo della definizione come luogo geometrico: parabola con asse verticale

Consideriamo una parabola con asse di simmetria verticale, ovvero una parabola avente equazione:

y=ax^2+bx+c, \qquad a \neq 0, \quad a,b,c \in \R

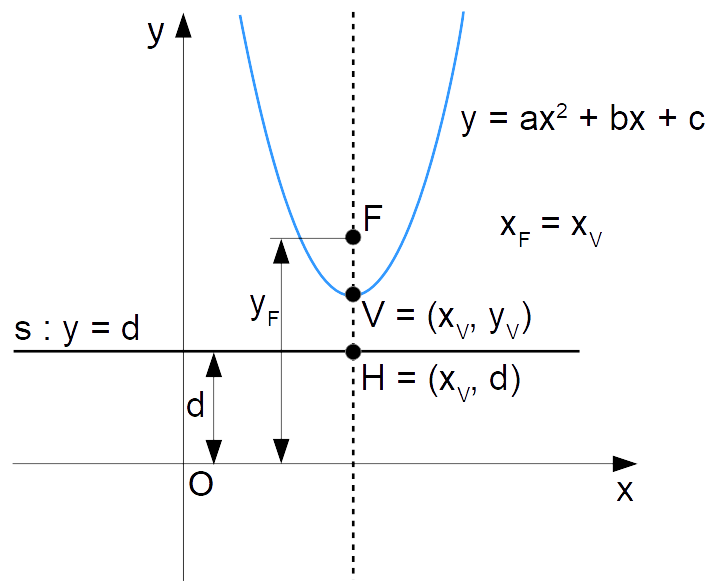
Indichiamo come al solito le coordinate del fuoco con {F=(x_F, y_F)}. Tali coordinate sono da determinare.

Osserviamo che poiché la parabola ha asse di simmetria verticale, l’ascissa del fuoco e l’ascissa del vertice coincidono:

x_F=x_V

Disponiamo così intanto del valore dell’ascissa del fuoco.

Il punto {H}, individuato dall’asse della parabola sulla direttrice, ha ascissa uguale a {x_V}. Inoltre, la sua ordinata è pari a {d}:

H=(x_V, d)

Il nostro obiettivo è determinare l’ordinata {y_F} del fuoco, in modo da poter poi scrivere l’equazione della parabola. Come sappiamo dalle precedenti lezioni, infatti, una volta note le coordinate del fuoco e l’equazione della direttrice è possibile determinare l’equazione della parabola a partire dalla sua definizione come luogo geometrico.

Osservando la figura è immediato comprendere che l’ordinata {y_F} è uguale alla somma della distanza con segno {d}, della lunghezza del segmento {\overline{VH}} e della lunghezza del segmento {\overline{VF}}:

y_F=d+\overline{VH}+\overline{VF}

Tuttavia, piuttosto che riferirci alle lunghezze geometriche preferiamo utilizzare le lunghezze algebriche. In tal modo, potremo ottenere per {y_F} un’espressione valida in tutti i casi (direttrice al di sopra o al di sotto dell’asse delle {x}, concavità della parabola rivolta verso l’alto o verso il basso).

Per la definizione di lunghezza algebrica si ha:

VH=y_H-y_V=d-y_V < 0

Nel caso in figura, la lunghezza algebrica {VH} risulta minore di zero.

Ora, per la definizione di parabola come luogo geometrico, dato che il vertice appartiene evidentemente alla parabola, si ha:

\overline{VF}=\overline{VH}

Così abbiamo intanto:

y_F=d+2 \cdot \overline{VH}

Ora, non resta che riesprimere l’uguaglianza appena scritta utilizzando la lunghezza algebrica {VH}. Per fare ciò, è fondamentale tenere conto che quest’ultima è nel caso in figura negativa. Così abbiamo:

y_F=d-2 \cdot  VH

Abbiamo infatti sottratto a {d} la quantità {2 \cdot VH} in modo da ottenere {y_F} come una quantità positiva maggiore di {d}, coerentemente al caso in figura.

Infine, ricordando che {VH=d-y_V} si ha:

y_F=d-2(d-y_V)=d-2d+2y_V=2y_V-d

e quindi:

\boxed{y_F=2y_V-d} \qquad \small \text{parabola con asse verticale}

Tale relazione consente di calcolare l’ordinata del fuoco a partire dall’ordinata del vertice e dalla distanza con segno {d} della direttrice rispetto all’asse {x}.

Ricordando ancora che l’ascissa del fuoco è nel caso di una parabola con asse verticale uguale all’ascissa del vertice, disponiamo in conclusione di entrambe le coordinate del fuoco. Disponendo inoltre anche dell’equazione della direttrice, ed essendo quindi nota la distanza con segno {d}, possiamo infine determinare l’equazione della parabola a partire dall’uguaglianza:

(x_F-x)^2+(y_F-y)^2=(y-d)^2

che corrisponde alla definizione di una parabola con asse verticale come luogo geometrico, relativa ad un generico punto della parabola stessa di coordinate {x} e {y}.

Esempio 3

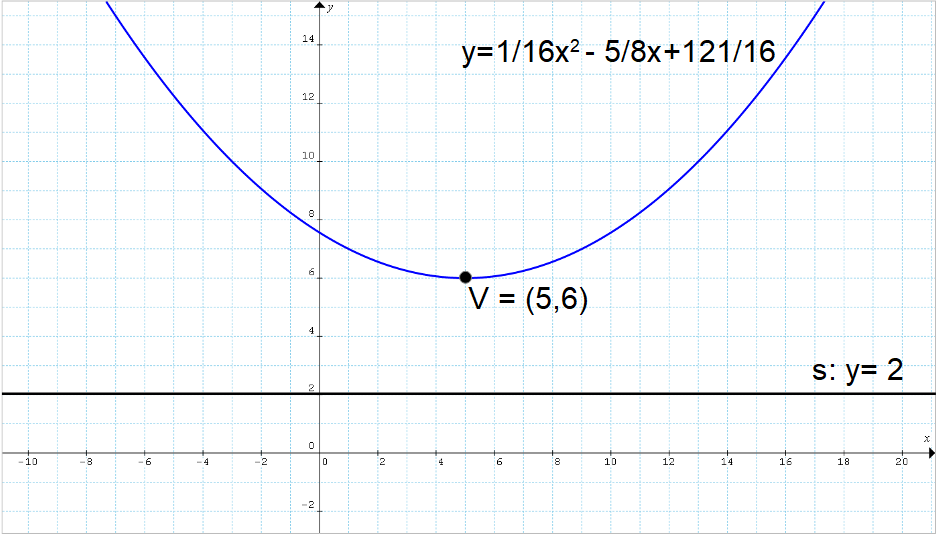
Determinare l’equazione della parabola avente vertice {V=(5,6)} e direttrice {s: y=2}.

Poiché la direttrice è una retta orizzontale, e poiché l’asse di una parabola è sempre perpendicolare alla direttrice, la parabola in esame ha asse di simmetria verticale.

Di conseguenza, l’ascissa del fuoco coincide con l’ascissa del vertice, che è nota. Quindi abbiamo intanto:

x_F=5

Inoltre, è possibile calcolare l’ordinata del fuoco come:

y_F=2y_V-d

Tenendo conto che in base all’equazione della direttrice data si ha per {d} il valore {2}, possiamo scrivere:

y_F=2 \cdot 6-2 \quad \Rightarrow \quad y_F=10

Ora non resta che sfruttare la definizione come luogo geometrico relativa ad una parabola con asse di simmetria verticale:

(x_F-x)^2+(y_F-y)^2=(y-d)^2

Ricordiamo che tale definizione equivale ad affermare che la distanza tra il generico punto della parabola di coordinate {x} e {y} e il fuoco {F} risulta uguale alla distanza tra quello stesso punto della parabola e la direttrice.

Così nel caso in esame abbiamo, sostituendo i valori delle coordinate del fuoco e della distanza con segno {d}:

(5-x)^2+(10-y)^2=(y-2)^2

e quindi:

\begin{align*} &25-10x+x^2+100-20y+\cancel{y^2}=\cancel{y^2}-4y+4; \\ \\ &(20-4)y=x^2-10x+25+100-4;\\ \\ & 16y=x^2-10x+121;\\ \\ & y=\dfrac{1}{16}x^2-\dfrac{5}{8}x+\dfrac{121}{16}\end{align*}

Abbiamo così ottenuto l’equazione della parabola data.

Verifica della formula per l’ordinata del fuoco

Ci proponiamo di verificare la formula:

y_F=2y_V-d

relativa al caso di una parabola con asse di simmetria verticale.

In primo luogo, osserviamo che tale formula si può ottenere ribaltando la formula vista nella lezione sulla parabola con fuoco e vertice, ovvero la formula:

d=2y_V-y_F

Infatti, esplicitando {y_F} si ha:

y_F=2y_V-d

Abbiamo così ritrovato la formula che dovevamo verificare.

In alternativa, possiamo sfruttare le espressioni in funzione dei coefficienti {a,b,c} corrispondenti all’ordinata del vertice e alla distanza {d} relative ad una parabola con asse verticale. Si ha in particolare:

y_V=-\dfrac{\Delta}{4a}

e:

\small d=-\dfrac{1+\Delta}{4a}

Così per la formula da verificare possiamo scrivere:

\begin{align*} &y_F=2y_V-d=2 \cdot \left( -\dfrac{\Delta}{4a}\right)-\left( -\dfrac{1+\Delta}{4a}\right)=\\ \\ & =\dfrac{-2\Delta+1+\Delta}{4a}=\dfrac{1-\Delta}{4a}=y_F\end{align*}

Effettivamente ritroviamo l’espressione per {y_F} nota dalle precedenti lezioni. Di conseguenza, la formula per {y_F} risulta anche in questo modo verificata.

Metodo della definizione come luogo geometrico: parabola con asse orizzontale

Vediamo come adattare il metodo appena visto al caso di una parabola con asse orizzontale, riferendoci quindi ad una parabola avente equazione in forma generale:

x=ay^2+by+c, \qquad a \neq 0, \quad a,b,c \in \R

Il nostro obiettivo, note le coordinate del vertice e l’equazione della direttrice, è quello di ricavare le coordinate del fuoco {F=(x_F, y_F)} e quindi scrivere l’equazione della parabola in esame sfruttando la sua definizione come luogo geometrico.

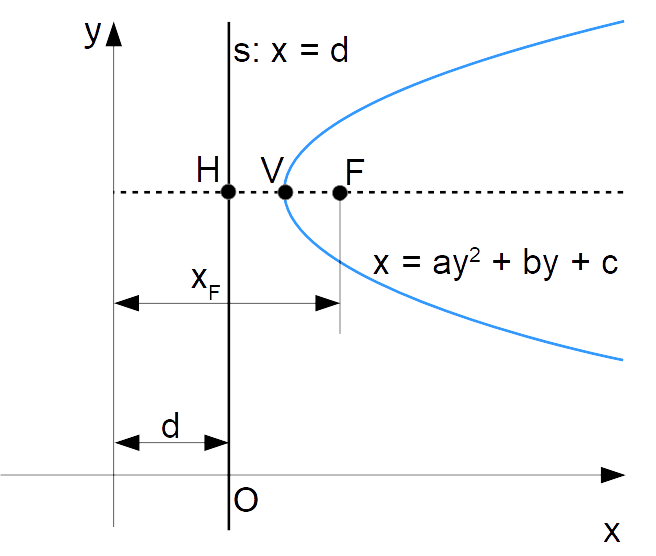
Poiché la parabola è ad asse orizzontale, si ha intanto:

y_F=y_V

quindi l’ordinata del fuoco è nota. Quanto all’ascissa, cominciamo osservando che per la lunghezza algebrica {VH} si ha:

VH=x_H-x_V=d-x_V<0

e tale quantità nel caso in figura è negativa.

Ora, per la definizione di parabola come luogo geometrico si ha:

\overline{VH}=\overline{VF}

Infatti il vertice {V} è un punto della parabola. Di conseguenza, sempre tenendo conto del caso in figura e viste le relazioni sinora scritte abbiamo:

\begin{align*} & x_F=d+\overline{VH}+\overline{VF}=d+2\cdot\overline{VH}=d-2 \cdot VH=\\ \\ & =d-2 \cdot(d-x_V)=d-2d+2x_V=2x_V-d \\ \\ & \Rightarrow \boxed{x_F=2x_V-d} \qquad \small \text{parabola con asse orizzontale} \end{align*}

Effettuando la verifica dell’uguaglianza appena scritta, abbiamo, in modo del tutto simile al caso di una parabola con asse verticale:

\begin{align*} &x_F=2x_V-d=2 \cdot \left( -\dfrac{\Delta}{4a}\right)-\left( -\dfrac{1+\Delta}{4a}\right)=\\ \\ & =\dfrac{-2\Delta+1+\Delta}{4a}=\dfrac{1-\Delta}{4a}=x_F\end{align*}

La verifica è positiva poiché effettivamente ritroviamo l’espressione data a suo tempo per {x_F}.

Osserviamo comunque che è possibile ricavare la formula per {x_F} anche a partire dalla seguente relazione, vista in una precedente lezione (parabola con fuoco e vertice, caso di una parabola con asse orizzontale):

d=2x_V-x_F

Infatti esplicitando {x_F} ritroviamo:

x_F=2x_V-d

Così in definitiva, nel caso di una parabola con asse orizzontale, note le coordinate del fuoco e l’equazione della direttrice, possiamo scriverne l’equazione a partire dalla sua definizione come luogo geometrico:

(x_F-x)^2+(y_F-y)^2=(x-d)^2

Vediamo subito un esempio.

Esempio 4

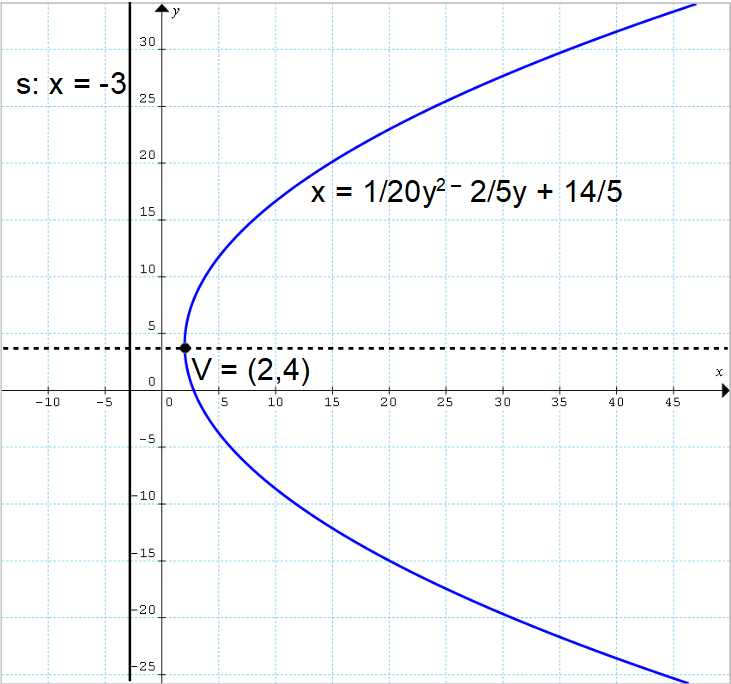
Determinare l’equazione della parabola avente vertice {V=(2,4)} e direttrice {s: x= -3}.

Poiché la direttrice è una retta verticale (retta formata da punti aventi tutti ascissa {-3}), l’asse della parabola, ad essa perpendicolare, è orizzontale. Di conseguenza, l’ordinata del fuoco sarà uguale all’ordinata del vertice, e quindi {y_F = 4}, mentre l’ascissa del fuoco sarà data da:

x_F=2x_V-d=2\cdot2-(\overbrace{-3}^{d})=4+3=7

Essendo ormai note le coordinate del fuoco e la distanza con segno {d} della direttrice rispetto all’asse {y}, possiamo scrivere:

\begin{align*} &(x_F-x)^2+(y_F-y)^2=(x-d)^2; \\ \\ & (7-x)^2+(4-y)^2=(x+3)^2; \\ \\ & 49-14x+\cancel{x^2}+16-8y+y^2=\cancel{x^2}+6x+9;\\ \\ & (6+14)x=y^2-8y+49+16-9;\\ \\ & 20x=y^2-8y+56; \\ \\ & x=\dfrac{1}{20}y^2-\dfrac{2}{5}y+\dfrac{14}{5} \end{align*}

Quella appena scritta è in conclusione l’equazione della parabola cercata, che corrisponde correttamente ad una parabola con asse orizzontale.

Conclusioni

Per quanto riguarda come determinare l’equazione di una parabola a partire dalle coordinate del vertice e dall’equazione della direttrice è tutto. Abbiamo in particolare visto come risolvere il problema utilizzando due differenti metodi. A voi la scelta del metodo a voi più congeniale, come sempre tenendo conto anche delle indicazioni del vostro insegnante.

Nella prossima lezione ci occuperemo del caso di una parabola passante per due punti e tangente ad una retta data. Proseguiremo così lo studio delle condizioni per individuare una parabola nel piano cartesiano. Tuttavia, le condizioni che esamineremo nella prossima lezione e in quella immediatamente successiva potranno individuare anche più di una parabola nel piano. E questa è un’importante differenza rispetto alle condizioni viste sinora.

Un saluto a tutti voi e buono studio!