Parabola con due punti e retta tangente

 - 

Parabola (scuole superiori)

L’equazione di una parabola con due punti noti e conoscendo una retta tangente si ottiene risolvendo un sistema nel quale sono presenti le condizioni di appartenenza di ciascun punto alla parabola e la condizione di tangenza della parabola alla retta data. In tal modo è possibile ricavare i valori dei coefficienti a, b, c che consentono di scrivere l’equazione della parabola cercata. Come ulteriore dato di partenza occorre conoscere la disposizione dell’asse della parabola (verticale od orizzontale), a meno che i due punti dati non risultino allineati verticalmente (parabola con asse orizzontale) o orizzontalmente (parabola con asse verticale), escludendo a priori il caso di parabole con asse obliquo.

In questa lezione vediamo quindi come trovare l’equazione di una parabola con asse verticale od orizzontale conoscendo le coordinate di due punti ad essa appartenenti e conoscendo l’equazione di una retta tangente alla parabola stessa. Osserviamo che è possibile trovare anche più di una parabola che rispetta le condizioni corrispondenti.

Come trovare l’equazione di una parabola noti due punti e l’equazione di una retta ad essa tangente

Vediamo come trovare l’equazione di una parabola conoscendo due punti ad essa appartenenti e l’equazione di una retta ad essa tangente, nei due distinti casi di parabola con asse verticale e orizzontale.

Parabola con due punti e una retta tangente: caso di una parabola con asse verticale

Consideriamo una parabola con asse verticale, la cui equazione è da determinare ma con forma generale:

\mathscr{P}: y=ax^2+bx+c, \qquad a \neq0, \quad a,b,c \in \R

Sono note le coordinate di due punti {P_1} e {P_2} appartenenti alla parabola:

P_1=(x_1,y_1), \qquad P_2=(x_2,y_2)

Inoltre, è anche nota l’equazione di una retta {r} tale da essere tangente alla parabola (essendo note le coordinate di due punti della parabola, non è necessario conoscere il punto di tangenza):

r:a_rx+b_ry+c_r=0

Il nostro obiettivo è determinare i coefficienti {a,b,c} in modo da poter scrivere l’equazione della parabola.

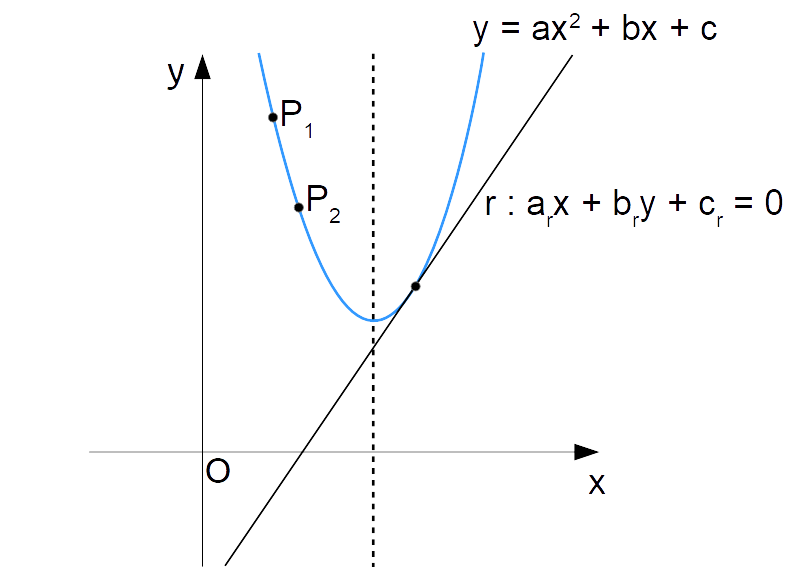
Ricordiamo anzitutto che se un punto appartiene alla parabola, le sue coordinate devono necessariamente soddisfare l’equazione della parabola stessa. Così, a ciascuno dei punti {P_1} e {P_2} corrisponderà una condizione di appartenenza alla parabola, come segue:

\begin{align*} &\boxed{y_1=ax_1^2+bx_1+c}, \qquad \text{condizione di appartenenza per }P_1 \\ \\ & \boxed{y_2=ax_2^2+bx_2+c},  \qquad \text{condizione di appartenenza per }P_2\qquad \end{align*}

Ora, per quanto riguarda la condizione di tangenza della retta {r} alla parabola, occorre prima di tutto considerare il sistema che rappresenta l’intersezione tra la parabola {\mathscr{P}} e la retta {r}:

\begin{cases}\mathscr{P}: y=ax^2+bx+c \\ \\ r: a_rx+b_ry+c_r\end{cases}

Il nostro obiettivo è in questo caso scrivere l’equazione risolvente del sistema, e quindi imporre che il suo determinante è uguale a zero. In tal modo otteniamo la condizione di tangenza della retta {r} alla parabola {\mathscr{P}}.

Cominciamo riscrivendo l’equazione della retta {r} in forma esplicita:

\begin{cases}\mathscr{P}: y=ax^2+bx+c \\ \\ r:y=\dfrac{-a_rx-c_r}{b_r}, \qquad b_r \neq 0\end{cases}

Osservazione. La condizione {b_r \neq 0} non è alcun modo restrittiva. Infatti, per {b_r = 0} la retta {r} diviene verticale, quindi parallela all’asse della parabola (che in questo caso è verticale). Ma una retta parallela all’asse della parabola sarà sempre secante alla parabola in un punto e mai tangente (vedi: intersezione tra una parabola e una retta).

Ora, sostituendo l’espressione appena ottenuta per {y} nella prima equazione otterremo l’equazione risolvente del sistema. Consideriamo tale equazione separatamente:

\begin{align*} &\dfrac{-a_rx-c_r}{b_r}=ax^2+bx+c; \\ \\ & \dfrac{-a_rx-c_r-ab_rx^2-bb_rx-b_rc}{b_r}=0; \\ \\ & -ab_rx^2+(-a_r-bb_r)x-c_r-b_rc=0, \qquad b_r \neq 0; \\ \\ & ab_rx^2+(a_r+bb_r)x+c_r+b_rc=0\end{align*}

Abbiamo in questo modo ottenuto l’equazione risolvente del sistema, che si presenta come un’equazione di secondo grado nella forma {Ax^2+Bx+C=0}, ponendo {A=ab_r, B = a_r+bb_r} e {C=c_r+b_rc}.

Poiché la retta {r} è tangente alla parabola, il determinante dell’equazione risolvente dovrà essere necessariamente uguale a zero:

\begin{align*} &B^2-4AC=0; \\ \\ & \boxed{(a_r+bb_r)^2-4 \cdot ab_r \cdot (c_r+b_rc)=0}\end{align*}

Abbiamo così ottenuto la condizione di tangenza della retta {r} alla parabola {\mathscr{P}}.

Mettendo insieme quest’ultima condizione con le due condizioni di appartenenza dei punti {P_1} e {P_2} alla parabola otteniamo il seguente sistema:

\begin{cases}ax_1^2+bx_1+c=y_1 \\ \\ ax_2^2+bx_2+c=y_2  \\ \\  (a_r+bb_r)^2-4 \cdot ab_r \cdot (c_r+b_rc)=0\end{cases} \qquad \small \text{parabola con asse verticale}

Sostituendo i valori delle coordinate dei punti {P_1} e {P_2} ed i valori dei coefficienti {a_r, b_r, c_r} della retta tangente, è possibile determinare i valori dei coefficienti {a,b,c} e quindi scrivere l’equazione della parabola cercata. E’ importante precisare che in questo caso potremmo ottenere anche due equazioni. Infatti, la terza equazione a sistema è di secondo grado rispetto a {b} (basta calcolare i prodotti per rendersene conto). Quindi, le parabole tali da soddisfare le condizioni richieste dal problema possono essere una o anche due.

Osserviamo infine che non è necessario ricordare o ricavare ogni volta la forma generale del sistema appena scritto. Piuttosto, è possibile ed anzi preferibile ricavare le condizioni da porre a sistema caso per caso (vedi esempio 2 a seguire). In ogni caso, il sistema “già pronto” può essere utile ai fini di verifica.

Esempio 1

Determinare l’equazione della parabola (o delle parabole) con asse verticale passante (o passanti) per i punti {P_1=(1,0), P_2= (3,22)} e tangente (o tangenti) alla retta {r: y=23x-55}.

Riesprimiamo l’equazione della retta in forma implicita:

r: 23x-y-55=0

Di conseguenza abbiamo {a_r = 23, b_r = -1 } e {c_r = -55}.

Utilizzando per questo primo esempio direttamente il sistema in forma generale abbiamo:

\begin{cases}ax_1^2+bx_1+c=y_1 \\ \\ ax_2^2+bx_2+c=y_2 \\ \\  (a_r+bb_r)^2-4 \cdot ab_r \cdot (c_r+b_rc)=0\end{cases}

Nel nostro caso per il punto {P_1} abbiamo le coordinate {x_1=1, y_1=0} e {x_2=3, y_2 = 22}. Inoltre, anche i coefficienti dell’equazione della retta {r} sono noti. Così, sostituendo nel sistema i valori a nostra disposizione abbiamo:

\begin{cases} a+b+c =0 \\ \\ 9a+3b+c=22 \\ \\ (23-b)^2-4 \cdot(-a)\cdot(-55-c)=0\end{cases}

ovvero:

\small \begin{cases} a+b+c =0 \\ \\ 9a+3b+c=22 \\ \\ 23^2-46b+b^2-(4 \cdot 55)a-4ac=0 \quad \rightarrow \quad 529-46b+b^2-220a-4ac=0\end{cases}

Ci ritroviamo quindi a dover risolvere il sistema:

\small \begin{cases} a+b+c =0 \\ \\ 9a+3b+c=22 \\ \\  -46b+b^2-220a-4ac=-529\end{cases}

Si tratta di un sistema non lineare (infatti l’incognita {b} compare con esponente maggiore di {1}), tuttavia possiamo risolvere il sistema con i metodi visti per i sistemi lineari.

Esplicitiamo l’incognita {c} dalla prima e dalla seconda equazione:

\small \begin{cases} c=-a-b \\ \\ c=22-9a-3b \\ \\  -46b+b^2-220a-4ac=-529\end{cases}

Sostituiamo alla seconda equazione una nuova equazione che otteniamo dal confronto delle prime due:

\begin{cases} c=-a-b \\ \\ -a-b=22-9a-3b \quad \rightarrow \quad 8a+2b=22\\ \\ -46b+b^2-220a-4ac=-529 \end{cases}

Ora sostituiamo l’espressione fornita per {c} dalla prima equazione nella terza equazione a sistema:

\begin{cases} c=-a-b \\ \\  8a+2b=22\\ \\ -46b+b^2-220a-4a \cdot (-a-b)=-529 \end{cases}

Otteniamo in questo modo:

\begin{cases} c=-a-b \\ \\  8a+2b=22\\ \\ -46b+b^2-220a+4a^2+4ab=-529 \end{cases}

Ora esplicitiamo la {a} dalla seconda equazione, e sostituiamo l’espressione per {a} che così otteniamo nella terza equazione:

\small \begin{cases} c=-a-b \\ \\  8a+2b=22 \quad \rightarrow \quad a=\dfrac{22-2b}{8} \quad \rightarrow \quad a=\dfrac{11}4{-\dfrac{1}{4}b}\\ \\ -46b+b^2-220\left( \dfrac{11}{4}-\dfrac{1}{4}b\right)+4\left( \dfrac{11}{4}-\dfrac{1}{4}b\right)^2+4\left( \dfrac{11}{4}-\dfrac{1}{4}b\right)b=-529 \end{cases}

Risolviamo separatamente la terza equazione, che ora è solo nell’incognita {b}:

\begin{align*} &-46b+b^2-605+55b+4 \left( \dfrac{121}{16}-\dfrac{11}{8}b+\dfrac{1}{16}b^2\right)+11b-b^2+529=0;\\ \\ & -46b+b^2-605+55b+\dfrac{121}{4}-\dfrac{11}{2}b+\dfrac{1}{4}b^2+11b-b^2+529=0;\\ \\ & \left( \cancel{1}+\dfrac{1}{4}-\cancel{1}\right)b^2+\left( -46+55-\dfrac{11}2{+11}\right)b-605+\dfrac{121}{4}+529=0;\\ \\ & \dfrac{1}{4}b^2+\dfrac{29}{2}b-\dfrac{183}{4}=0\end{align*}

Riprendendo il sistema abbiamo quindi:

\small \begin{cases} c=-a-b \\ \\   a=\dfrac{11}4{-\dfrac{1}{4}b}\\ \\  \dfrac{1}{4}b^2+\dfrac{29}{2}b-\dfrac{183}{4}=0\end{cases}

Risolviamo la terza equazione rispetto a {b}:

\begin{align*} &b_{1,2}=\dfrac{-\dfrac{29}{2}\pm \sqrt{\left( \dfrac{29}{2}\right)^2-4 \cdot \dfrac{1}4{\cdot \left( -\dfrac{183}{4}\right)}}}{\dfrac{1}{2}}=\\ \\ & =\left({-\dfrac{29}{2}\pm \sqrt{\dfrac{841+183}{4}}}\right)\cdot 2 =-29 \pm 32 = \begin{cases} 3 \\ \\ -61\end{cases}\end{align*}

Otteniamo così per il coefficiente {b} i due valori {3} e {-61}. Di conseguenza, l’equazione appena risolta fornisce:

b=3 \quad \vee \quad b=-61

e quindi il precedente sistema diviene:

\small \begin{cases} c=-a-b \\ \\   a=\dfrac{11}4{-\dfrac{1}{4}b}\\ \\ b=3 \quad \vee \quad b=-61\end{cases}

Come visto nella lezione sui sistemi non lineari, possiamo riesprimere il sistema dato come:

\small \begin{cases} c=-a-b \\ \\   a=\dfrac{11}4{-\dfrac{1}{4}b}\\ \\ b=3\end{cases} \qquad \vee \qquad \begin{cases} c=-a-b \\ \\   a=\dfrac{11}4{-\dfrac{1}{4}b}\\ \\ b=-61\end{cases} 

e le soluzioni del sistema di partenza saranno dati dall’unione degli insiemi delle soluzioni di ciascuno dei due sistemi appena scritti.

Il sistema a sinistra fornisce:

\small \begin{cases} c=-a-b \\ \\   a=\dfrac{11}4{-\dfrac{1}{4}b}\\ \\ b=3\end{cases}  \quad \Rightarrow \quad \begin{cases} c=-a-3; \qquad c=-2-3 \quad \rightarrow \quad c=-5 \\ \\ a=\dfrac{11}4{-\dfrac{1}{4} \cdot 3 \quad \rightarrow \quad a=2} \\ \\ b=3\end{cases}

Così intanto abbiamo per il sistema di partenza una prima soluzione data dalla terna di valori {a=2, b = 3 } e {c=-5}. Di conseguenza, una prima parabola tale da soddisfare le condizioni richieste dal problema è:

\mathscr{P}_1:  y=2x^2+3x-5

L’equazione appena scritta si ottiene sostituendo nell’equazione della generica parabola con asse verticale i valori appena trovati per i coefficienti {a,b,c}.

Considerando il sistema di destra e procedendo allo stesso modo abbiamo:

\begin{cases} c=-a-b ; \qquad c=-18+61 \quad \rightarrow \quad c=43\\ \\   a=\dfrac{11}4{-\dfrac{1}{4}b} \quad \rightarrow \quad a=\dfrac{11}{4}-\dfrac{1}{4} \cdot (-61) \quad \rightarrow \quad a=18\\ \\ b=-61\end{cases} 

Così otteniamo una seconda parabola avente equazione:

\mathscr{P}_2: y=18x^2-61x+43

Le parabole {\mathscr{P}_1 } e {\mathscr{P}_2} sono in conclusione le due parabole del piano cartesiano tali da passare per i punti {P_1} e {P_2} dati e tali da avere come tangente in un certo punto la retta {r}.

Per questo primo esempio abbiamo visto come determinare la parabola (o le parabole) passanti per due punti dati e tangenti ad una assegnata retta utilizzando un sistema “preconfezionato”. Nell’esempio a seguire vedremo come cavarcela senza dover ricordare il sistema nella forma generale.

Esempio 2

Determinare l’equazione della parabola o delle parabole con asse verticale passanti per i punti {P_1=(1,3)} e {P_2=(4,12)} e aventi come tangente in un dato punto la retta di equazione {r:y=8x-21}.

Le condizioni di appartenenza della parabola (o delle parabole) ai punti {P_1} e {P_2} sono immediate. Tenendo conto che le parabole che stiamo cercando hanno asse verticale si ha:

\begin{align*} &\boxed{a+b+c=3}, \qquad \text{appartenenza a }P_1 \\ \\ &\boxed{16a+4b+c=12}, \qquad \text{appartenenza a }P_2\end{align*}

Vediamo ora di ottenere l’equazione esprimente la condizione di tangenza della parabola (o parabole) rispetto alla retta {r}. Partiamo dal sistema, che rappresenta l’intersezione tra la generica parabola e la retta {r}

\begin{cases} y=ax^2+bx+c \\ \\ r: y=8x-21\end{cases}

Applicando il metodo del confronto si ottiene l’equazione risolvente:

\begin{align*} &8x-21=ax^2+bx+c; \\ \\ & \underbrace{a}_{A}x^2+\underbrace{(b-8)}_{B}x+\underbrace{c+21}_{C}=0\end{align*}

Imponiamo che il determinante dell’equazione risolvente sia uguale a zero (condizione di tangenza della retta {r} alla parabola):

\begin{align*} & B^2-4AC=0;\\ \\  & (b-8)^2- 4 \cdot a \cdot (c+21)=0; \\ \\ & b^2-16b+64-4ac-84a=0; \\ \\ & \boxed{b^2-16b-4ac-84a+64=0} \end{align*}

Il sistema da risolvere per determinare i valori dei coefficienti {a,b,c} è formato dalle equazioni corrispondenti alle tre condizioni evidenziate nei riquadri:

\begin{cases} a+b+c=3 \\ \\ 16a+4b+c=12 \\ \\ b^2-16b-4ac-84a+64=0 \end{cases}

Come verifica facoltativa, il sistema scritto è corretto in quanto è possibile ritrovarlo sostituendo i valori corrispondenti ai dati di partenza nel sistema in forma generale relativo a parabole con asse verticale.

Risolvendo il sistema con lo stesso metodo visto nell’esempio precedente otteniamo le due soluzioni, date dalle due terne di valori (omettiamo per brevità lo svolgimento):

a=1, \qquad b=-2, \qquad c=4

e:

a=\dfrac{25}{9}, \qquad b=-\dfrac{98}{9}, \qquad c=\dfrac{100}{9}

In conclusione, a ciascuna terna di valori per i coefficienti {a,b,c} corrispondono rispettivamente le parabole:

\mathscr{P}_1: y=x^2-2x+4, \qquad \mathscr{P}_2:y=\dfrac{25}{9}x^2-\dfrac{98}{9}x+\dfrac{100}{9}

che rappresentano le equazioni delle parabole passanti per i punti {P_1, P_2} e aventi ciascuna in un dato punto come retta tangente la retta {r}.

Parabola con due punto e una retta tangente: caso di una parabola con asse orizzontale

Consideriamo una parabola con asse orizzontale, la cui equazione è da determinare ma avente equazione in forma generale:

\mathscr{P}: x=ay^2+by+c, \qquad a \neq0, \quad a,b,c \in \R

Ancora, disponiamo delle coordinate di due punti {P_1} e {P_2} appartenenti alla parabola:

P_1=(x_1,y_1), \qquad P_2=(x_2,y_2)

Inoltre, è anche nota l’equazione di una retta {r} tale da essere tangente alla parabola (non è necessario in questo caso conoscere il punto di tangenza):

r:a_rx+b_ry+c_r=0

Il nostro obiettivo è ancora quello di determinare i coefficienti {a,b,c}, in modo da poter scrivere l’equazione della parabola.

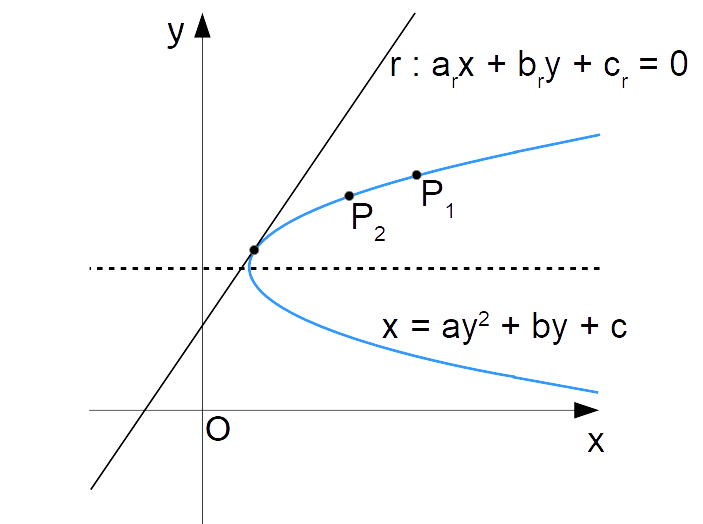
A ciascuno dei punti {P_1} e {P_2} corrisponderà una condizione di appartenenza alla parabola, come segue:

\begin{align*} &\boxed{x_1=ay_1^2+by_1+c}, \qquad \text{condizione di appartenenza per }P_1 \\ \\ & \boxed{x_2=ay_2^2+by_2+c},  \qquad \text{condizione di appartenenza per }P_2\qquad \end{align*}

Ora, per quanto riguarda la condizione di tangenza della retta {r} alla parabola, come visto nel caso precedente occorre prima di tutto considerare il sistema che rappresenta l’intersezione tra la parabola {\mathscr{P}} e la retta {r}:

\begin{cases}\mathscr{P}: x=ay^2+by+c \\ \\ r: a_rx+b_ry+c_r\end{cases}

Il nostro obiettivo è anche in questo caso scrivere l’equazione risolvente del sistema, e quindi imporre che il suo determinante è uguale a zero. In tal modo otteniamo la condizione di tangenza della retta {r} alla parabola {\mathscr{P}}.

Cominciamo riscrivendo l’equazione della retta {r} esplicitando la variabile {x}:

\begin{cases}\mathscr{P}: x=ay^2+by+c \\ \\ x=\dfrac{-b_ry-c_r}{a_r}, \qquad a_r \neq 0\end{cases}

Osservazione. La condizione {a_r \neq 0} non è alcun modo restrittiva. Infatti, per {a_r = 0} la retta {r} diviene orizzontale, quindi parallela all’asse della parabola (che in questo caso è orizzontale). Ma una retta parallela all’asse della parabola sarà sempre secante alla parabola in un punto e mai tangente (vedi: intersezione tra una parabola e una retta).

Ora, sostituendo l’espressione appena ottenuta per {x} nella prima equazione otterremo l’equazione risolvente del sistema. Consideriamo tale equazione separatamente:

\begin{align*} &\dfrac{-b_ry-c_r}{a_r}=ay^2+by+c; \\ \\ & \dfrac{-b_ry-c_r-aa_ry^2-a_rby-a_rc}{a_r}=0; \\ \\ &{aa_ry^2+(b_r+a_rb)y+c_r+a_rc=0}, \qquad a_r\neq0 \end{align*}

Abbiamo in questo modo ottenuto l’equazione risolvente del sistema, che si presenta come un’equazione di secondo grado nella forma {Ay^2+By+C}, ponendo {A=aa_r, B = b_r+a_rb} e {C=c_r+a_rc}.

Poiché la retta {r} è tangente alla parabola, il determinante dell’equazione risolvente dovrà essere necessariamente uguale a zero:

\begin{align*} &B^2-4AC=0; \\ \\ &\boxed{(b_r+a_rb)^2-4 \cdot aa_r \cdot (c_r+a_rc)=0} \end{align*}

Abbiamo così ottenuto la condizione di tangenza della retta {r} alla parabola {\mathscr{P}} avente asse orizzontale.

Mettendo insieme quest’ultima condizione con le due condizioni di appartenenza dei punti {P_1} e {P_2} alla parabola otteniamo il seguente sistema:

\begin{cases}ay_1^2+by_1+c=x_1 \\ \\ ay_2^2+by_2+c=x_2  \\ \\  (b_r+a_rb)^2-4 \cdot aa_r \cdot (c_r+a_rc)=0 \end{cases} \qquad \small \text{parabola con asse orizzontale}

Sostituendo i valori delle coordinate dei punti {P_1} e {P_2} ed i valori dei coefficienti {a_r, b_r, c_r} della retta tangente, è possibile determinare i valori dei coefficienti {a,b,c} e quindi scrivere l’equazione della parabola cercata. In modo del tutto simile al caso di una parabola con asse verticale, potremmo anche in questa circostanza ottenere non necessariamente una ma anche due parabole tali da soddisfare le condizioni poste dal problema.

Ed inoltre, come osservato in precedenza, non è necessario ricordare o ricavare ogni volta la forma generale del sistema appena scritta. Piuttosto, è possibile e preferibile ricavare le condizioni da porre a sistema caso per caso. Utilizzeremo quest’ultimo approccio nell’esempio 4 a seguire.

Esempio 3

Determinare l’equazione della parabola (o delle parabole) con asse orizzontale, passanti per i punti {P_1=(4, 1)} e {P_2=(4,-3)}, ed inoltre tali da avere come tangente in un dato punto la retta {r:x-4y+2=0 }.

Nota: osserviamo che i due punti {P_1} e {P_2} hanno la stessa ascissa e quindi sono allineati verticalmente. E poiché tali punti appartengono alla parabola, è immediato dedurre che la parabola stessa ha asse di simmetria orizzontale. Per cui l’informazione relativa alla disposizione dell’asse della parabola avrebbe anche potuto essere omessa nel testo del problema. Ci occuperemo comunque di questo aspetto alla fine della lezione.

In base ai dati forniti dal problema abbiamo {x_1=4, y_1 = 1, x_2 = 4, y_2 = -3, a_r=1, b_r=-4} ed infine {c_r=2}. Così, il sistema in forma generale:

\begin{cases}ay_1^2+by_1+c=x_1 \\ \\ ay_2^2+by_2+c=x_2  \\ \\  (b_r+a_rb)^2-4 \cdot aa_r \cdot (c_r+a_rc)=0 \end{cases}

diviene nel nostro caso:

\begin{cases} a+b+c=4 \\ \\ 9a-3b+c=4 \\ \\ (-4+b)^2-4 a \cdot (2+c)=0 \quad \rightarrow \: 16-8b+b^2-8a-4ac=0\end{cases}

Il metodo per risolvere il sistema è del tutto simile a quello visto nei casi precedenti. Svolgiamo comunque i passaggi per allenamento. Esplicitando la {c} dalla prima e dalla seconda equazione abbiamo:

\begin{cases}c=4-a-b \\ \\ c=4-9a+3b \\ \\  16-8b+b^2-8a-4ac=0\end{cases}

Procedendo per confronto:

\begin{cases} c=4-a-b \\ \\ \cancel{4}-a-b=\cancel{4}-9a+3b \quad \rightarrow \: 8a=4b \quad \rightarrow \: b=2a \\ \\  16-8b+b^2-8a-4ac=0\end{cases}

Sostituendo l’espressione appena ottenuta per {b} nelle rimanenti equazioni e sostituendo anche l’espressione che fornisce la prima equazione per {c} nella terza equazione, si ha:

\begin{cases} c=4-a-2a \quad \rightarrow \quad c=4-3a \\ \\ b=2a \\ \\ 16-16a+4a^2-8a-4a(4-a-b) = 0\end{cases}

E quindi:

\begin{cases} c=4-3a \\ \\ b=2a \\ \\ 16-24a+4a^2-16a+4a^2+4ab=0 \quad \rightarrow \: 8a^2-40a+16+4a \cdot(2a) = 0 \end{cases}

ovvero:

\begin{cases} c=4-3a \\ \\ b=2a \\ \\  8a^2-40a+16+8a^2 = 0 \quad \rightarrow \: 16a^2-40a+16=0 \quad \rightarrow \: 2a^2-5a+2=0 \end{cases}

Otteniamo così il sistema:

\begin{cases} c=4-3a \\ \\ b=2a \\ \\ 2a^2-5a+2=0\end{cases}

Risolviamo separatamente la terza equazione:

\begin{align*} &2a^2-5a+2=0; \\ \\ & a_{1,2}=\dfrac{5 \pm \sqrt{25-16}}{4}=\dfrac{5 \pm 3}{4}=\begin{cases} 2 \\ \\ \dfrac{1}{2}\end{cases}\end{align*}

Di conseguenza il sistema diviene:

\begin{cases} c=4-3a \\ \\ b=2a \\ \\ a=2 \quad \vee \quad a = \dfrac{1}{2}\end{cases}

e quindi, per quanto sappiamo sui sistemi non lineari:

\begin{cases} c=4-3a \\ \\ b=2a \\ \\ a=2 \end{cases} \qquad \vee \qquad  \begin{cases} c=4-3a \\ \\ b=2a \\ \\ a=\dfrac{1}{2}\end{cases}

Risolvendo ciascun sistema per sostituzione, otteniamo:

\begin{cases} c=-2 \\ \\ b=4 \\ \\ a = 2 \end{cases} \qquad \vee \qquad \begin{cases} c=\dfrac{5}{2} \\ \\ b=1 \\ \\ a=\dfrac{1}{2}\end{cases}

Abbiamo così due soluzioni per il sistema, data ciascuna da una terna di valori per i coefficienti {a,b,c}. In corrispondenza abbiamo le parabole con asse orizzontale (vedi testo del problema) di equazione:

\mathscr{P}_1: x=2y^2+4y-2; \qquad \mathscr{P}_2: x=\dfrac{1}{2}y^2+y+\dfrac{5}{2}

Queste sono le due parabole che soddisfano le condizioni date dal problema in esame. In particolare, i punti {P_1} e {P_2} risultano appartenenti ad entrambe le parabole e la retta {r} data nel testo risulta tangente ad entrambe.

Esempio 4

Determinare l’equazione della parabola (o delle parabole) con asse orizzontale passanti per i punti {P_1=(-4, 0), P_2=(-5,1)} e con retta ad essa tangente in un punto {r:x-5y+12=0 }.

Vediamo il procedimento risolutivo in forma molto sintetica, dato che ormai tutto dovrebbe essere chiaro dagli esempi precedenti.

Per le condizioni di passaggio nei due punti {P_1} e {P_2} abbiamo, rispettivamente:

\begin{align*} &c=-4; \qquad a+b+c=-5 \end{align*}

Imponiamo la tangenza della retta {r} rispetto alla parabola in esame:

\small \begin{cases} x=ay^2+by+c \\ \\ x=5y-12\end{cases} \quad \Rightarrow \quad 5y-12-ay^2-by-c=0 \quad \Rightarrow \: ay^2+(b-5)y+12+c=0

\begin{align*} &\Delta = 0; \\ \\ & (b-5)^2-4 \cdot a \cdot (c+12)=0;\\ \\ & b^2-10b+25-4ac-48a=0\end{align*}

Così per determinare i coefficienti {a,b,c} dell’equazione della parabola occorrerà risolvere il sistema:

\begin{cases} c=-4 \\ \\  a+b+c=-5  \\ \\ b^2-10b+25-4ac-48a=0 \end{cases}

Risolvendo il sistema per sostituzione otteniamo come soluzioni le due terne:

a=2, \: b=-3, \: c=-4; \qquad a=18, \: b=-19, \: c=-4

alle quali corrispondono rispettivamente le parabole:

\mathscr{P}_1: x=2y^2-3y-4; \qquad \mathscr{P}_2:x=18y^2-19y-4

Conclusioni

Abbiamo visto nella lezione come determinare l’equazione della parabola (o delle parabole) passanti per due punti ed aventi per tangente in un certo punto una retta assegnata. Osserviamo, prima di salutarci, che anche il problema della ricerca delle equazioni di parabole passanti per un punto e tangenti ad una certa retta in un punto di coordinate note è comunque riconducibile ai casi sin qui visti. Infatti, se è noto il punto di tangenza, questo è comunque un punto appartenente alla parabola. Di conseguenza, ci ritroviamo di nuovo nel caso di due punti noti e di equazione di una retta tangente nota. In particolare, le coordinate del punto di tangenza ci permetteranno di scrivere due condizioni, ovvero la condizione di appartenenza del punto alla parabola e la condizione di tangenza della retta data in quel punto. La terza condizione sarà ovviamente data dall’appartenenza del rimanente punto alla parabola.

Consideriamo ad esempio il problema del determinare l’equazione della parabola passante per {P=(0,-4)} e tangente nell’origine alla retta {y=\dfrac{1}{8}x}.

Osserviamo che il punto {P} e l’origine {O=(0,0)} sono allineati verticalmente, e sono punti appartenenti alla parabola. Per cui, l’unica è che la parabola abbia asse orizzontale. Infatti, ci ritroviamo in una situazione del tutto simile al caso generale riportato in figura a sinistra:

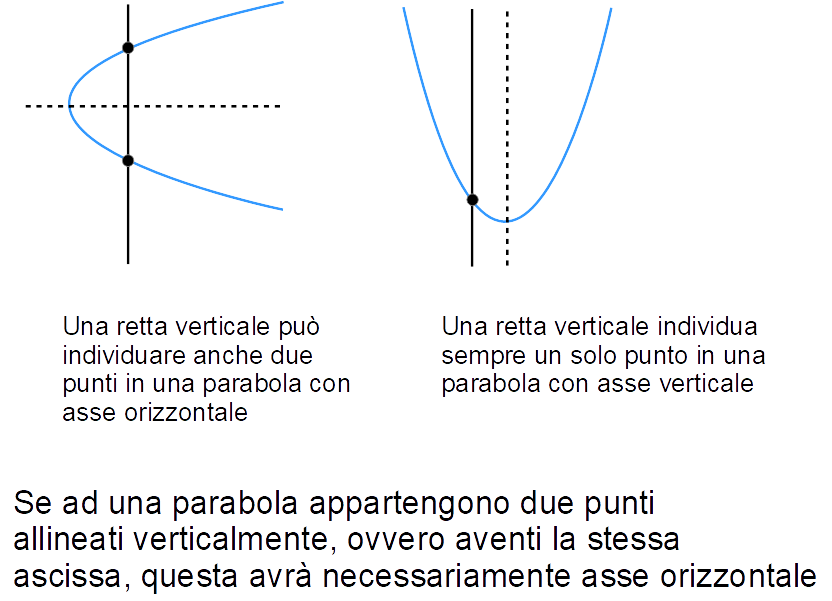
Tra parentesi, allo stesso modo se ad una parabola appartengono due punti allineati orizzontalmente, ovvero aventi la stessa ordinata, la parabola avrà necessariamente asse verticale.

Importante. Le considerazioni fatte sono valide escludendo ovviamente i casi di parabole con asse obliquo.

Ora, tornando al nostro caso, dato che il punto {P} e l’origine degli assi {O=(0,0)} appartengono entrambi alla parabola, abbiamo rispettivamente le condizioni di appartenenza:

16a-4b+c=0; \qquad c=0

La condizione {c=0} effettivamente corrisponde ad una parabola passante per l’origine.

Quanto alla condizione di tangenza, impostiamo il sistema:

\begin{cases} x=ay^2+by+c \\ \\ r: y=\dfrac{1}{8}x\end{cases}

Esplicitando la variabile {x} nell’equazione della retta ed applicando il metodo del confronto si ha:

\begin{cases} x=ay^2+by+c \\ \\ r: x=8y\end{cases} \quad \Rightarrow \quad 8y=ay^2+by+c \quad \Rightarrow \: ay^2+(b-8)y+c=0

Imponendo che il determinante dell’equazione appena scritta sia uguale a zero (condizione di tangenza della retta {r} alla parabola):

\begin{align*} &(b-8)^2-4ac=0; \\ \\ & b^2-16b+64-4ac=0;\\ \\ & b^2-16b-4ac+64=0\end{align*}

Per determinare i coefficienti {a,b,c} dovremo quindi risolvere il sistema dato dalle condizioni di appartenenza del punto {P} e dell’origine alla parabola, più la condizione di determinante nullo appena scritta:

\begin{cases} 16a-4b+c=0 \\ \\ c=0 \\ \\ b^2-16b-4ac+64=0\end{cases} \quad \Rightarrow \quad \begin{cases} 16a-4b=0 \\ \\ c=0 \\ \\ b^2-16b+64=0\end{cases}

Consideriamo separatamente la terza equazione:

\begin{align*} &b^2-16b+64=0; \\ \\ & b_{1,2}={8\pm\sqrt{64-64}}=8\end{align*}

Otteniamo due soluzioni reali e coincidenti e quindi a lato pratico un solo valore per il coefficiente {b}. Di conseguenza, ci ritroviamo con un solo sistema:

\begin{cases} 16a-4b=0 \quad \rightarrow \quad a=2 \\ \\ c=0 \\ \\ b=8\end{cases}

Per cui in conclusione la parabola che soddisfa le condizioni imposte dal problema in esame è una sola ed ha equazione (ricordiamo che ha asse orizzontale):

\mathscr{P}: x=2y^2+8y

Ora è davvero tutto. Un caro saluto a tutti voi e buono studio!