Parabola con punto e equazioni dell’asse e della direttrice

 - 

Parabola (scuole superiori)

L’equazione di una parabola con le coordinate di un punto e le equazioni dell’asse di simmetria e della direttrice si può scrivere impostando un sistema contenente la condizione di appartenenza del punto alla parabola e delle uguaglianze fra le opportune espressioni in funzione dei coefficienti a, b, c e rispettivamente il secondo membro dell’equazione dell’asse e la distanza con segno d.

In alternativa, l’equazione di una parabola con punto e equazioni dell’asse di simmetria e della direttrice si può anche ottenere sfruttando la definizione di luogo geometrico della parabola. Seguendo tale approccio, l’idea è quella di ricavare la coordinata mancante del fuoco della parabola, e quindi scrivere l’equazione della parabola sfruttando la definizione di luogo geometrico, poiché a tal punto entrambe le coordinate del fuoco e la distanza con segno d sono note.

In questa lezione proseguiamo quindi lo studio delle condizioni per determinare l’equazione di una parabola, riferendoci all’ultimo caso di una parabola della quale siano note le coordinate di un punto e le equazioni dell’asse e della direttrice. Vedremo in particolare come sia possibile impostare un sistema non lineare in modo da ottenere i coefficienti a, b, c relativi all’equazione della parabola, oppure in alternativa presenteremo il metodo che sfrutta la definizione di parabola come luogo geometrico. Questo secondo metodo si basa sulla circostanza ormai nota per la quale è possibile scrivere l’equazione di una parabola una volta note le coordinate del fuoco e la distanza con segno d.

Parabola con punto e equazioni dell’asse e della direttrice: parabola con asse verticale

Cominciamo ad esaminare i due possibili metodi nel caso di una parabola con asse di simmetria verticale. Nella parte successiva della lezione, considereremo questi due stessi metodi anche nel caso di una parabola con asse di simmetria orizzontale.

Metodo del sistema (parabola con asse di simmetria verticale, con punto ed equazioni di asse e direttrice)

Consideriamo una parabola con asse di simmetria verticale, la cui equazione è da determinare ma che si presenta in forma generale come:

y=ax^2+bx+c, \qquad a \neq 0, \quad a,b,c \in \R

Come dati di partenza, sappiamo anzitutto che un punto {P_1=(x_1, y_1)} di coordinate note appartiene alla parabola. Da ciò discende la condizione di appartenenza:

\boxed{ax_1^2+bx_1+c=y_1}

Infatti, se un punto appartiene alla parabola, le sue coordinate devono soddisfare l’equazione della parabola stessa.

Inoltre, abbiamo l’equazione dell’asse della parabola:

x=h

e l’equazione della direttrice:

s: y=d

Entrambi {h} e {d} sono dei valori reali noti.

Ricordando le espressioni delle equazioni dell’asse di simmetria e della direttrice in funzione dei coefficienti {a,b,c} per una parabola con asse verticale, dalle due precedenti equazioni possiamo ricavare le condizioni:

\boxed{-\dfrac{b}{2a}=h}; \qquad \boxed{-\dfrac{1+\Delta}{4a}=d}

A partire dai dati di partenza abbiamo così scritto in tutto tre condizioni, evidenziate nei riquadri. E infine, poiché tali condizioni devono valere contemporaneamente ci ritroviamo con il sistema:

\begin{cases} ax_1^2+bx_1+c=y_1 \\ \\  -\dfrac{b}{2a}=h \\ \\-\dfrac{1+\Delta}{4a}=d  \end{cases}

ovvero ricordando che {\Delta = b^2-4ac}:

\begin{cases} ax_1^2+bx_1+c=y_1 \\ \\  -\dfrac{b}{2a}=h \\ \\\dfrac{4ac-1-b^2}{4a}=d  \end{cases} \qquad \text{parabola con asse verticale}

Il sistema è del tipo non lineare ma può essere risolto per sostituzione, in modo simile al caso dei sistemi lineari. Una volta risolto, il sistema fornisce i valori dei coefficienti {a,b,c} che corrispondono alla parabola (o alle parabole) tali da rispettare le condizioni date dal problema in esame.

Come nel caso visto nella precedente lezione di una parabola con passaggio per due punti ed equazione di una retta tangente, anche nel caso in esame potremmo ottenere anche due parabole. Infatti, la terza equazione a sistema è di secondo grado rispetto a {b}.

Vediamo subito un esempio.

Esempio 1

Determinare l’equazione di una parabola o delle parabole tali da avere asse di simmetria di equazione {x=-1}, direttrice di equazione {y=-\dfrac{29}{4}} e tali da passare per il punto {P_1=(1,-3)}.

Osserviamo prima di tutto che l’asse di simmetria è una retta verticale. Di conseguenza, la parabola o le parabole che cerchiamo sono del tipo ad asse verticale, quindi con equazione della forma generale:

y=ax^2+bx+c, \qquad a \neq 0, \quad a,b,c \in \R

Dal confronto dell’equazione dell’asse di simmetria nella forma generale {x=h} con l’equazione data {x=-1} abbiamo {h=-1}. Inoltre, dal confronto della forma generale dell’equazione della direttrice {y=d} con l’equazione {y=-\dfrac{29}{4}} relativa al nostro caso abbiamo {d=-\dfrac{29}{4}}.

Inoltre, al punto {P_1=(1,-3)} appartenente alla parabola corrispondono le coordinate {x_1 = 1} e {y_1=-3}. Quindi, tenendo conto di tutti i dati, partendo dal sistema in forma generale:

\begin{cases} ax_1^2+bx_1+c=y_1 \\ \\  -\dfrac{b}{2a}=h \\ \\\dfrac{4ac-1-b^2}{4a}=d  \end{cases} 

possiamo scrivere, sostituendo i valori:

\begin{cases} a+b+c=-3 \\ \\  -\dfrac{b}{2a}=-1 \\ \\\dfrac{4ac-1-b^2}{4a}=-\dfrac{29}{4}  \end{cases} 

Il sistema è del tipo non lineare ma si può risolvere per sostituzione. Cominciamo ricavando un’espressione per {b} dalla seconda equazione:

\begin{cases} a+b+c=-3 \\ \\  -\dfrac{b}{2a}=-1 \quad \rightarrow \quad b=2a\\ \\\dfrac{4ac-1-b^2}{4a}=-\dfrac{29}{4}  \end{cases} 

Sostituiamo l’espressione ottenuta per {b} nelle altre due equazioni:

\begin{cases} a+2a+c=-3 \quad \rightarrow \quad 3a+c=-3 \\ \\ b=2a\\ \\ \dfrac{4ac-1-(2a)^2}{4a}=-\dfrac{29}{4} \quad \rightarrow \quad \dfrac{4ac-1-4a^2}{4a}=-\dfrac{29}{4}\end{cases}

Ora ricaviamo un’espressione per {c} dalla prima equazione, e quindi sostituiamola nella terza equazione:

\begin{cases}  3a+c=-3 \quad \rightarrow \quad c=-3-3a \\ \\ b=2a\\ \\ \dfrac{4ac-1-4a^2}{4a}=-\dfrac{29}{4} \quad \rightarrow \quad \dfrac{4a(-3-3a)-1-4a^2}{4a}=-\dfrac{29}{4}\end{cases}

Ora la terza equazione è nella sola incognita {a}. Considerandola separatamente abbiamo:

\begin{align*} &\dfrac{-12a-12a^2-1-4a^2}{4a}+\dfrac{29}{4}=0;\\ \\ & \dfrac{-12a-16a^2-1+29a}{4a}=0;\\ \\ & -16a^2+17a-1=0, \qquad a \neq0 ;\\ \\ & 16a^2-17a+1=0; \\ \\ & a_{1,2}=\dfrac{17\pm \sqrt{289-4 \cdot 16 \cdot 1}}{32}=\dfrac{17 \pm 15 }{32}= \begin{cases} 1 \\ \\ \dfrac{1}{16}\end{cases}\end{align*}

Il sistema diviene quindi:

\begin{cases}  c=-3-3a \\ \\ b=2a\\ \\a=1 \quad \vee \quad a=\dfrac{1}{16}\end{cases}

e ricordando quanto visto nella lezione sui sistemi non lineari:

\begin{cases}  c=-3-3a \\ \\ b=2a\\ \\a=1 \end{cases} \qquad \vee \qquad \begin{cases} c=-3-3a \\ \\ b=2a \\ \\ a=\dfrac{1}{16}\end{cases}

Le soluzioni del sistema di partenza saranno quindi date dall’unione delle soluzioni del sistema a sinistra e del sistema a destra. Abbiamo, procedendo per sostituzione in ciascun sistema:

\begin{cases}c=-6\\ \\  b=2\\ \\ a=1\end{cases} \qquad \vee \qquad \begin{cases} c=-\dfrac{51}{16} \\ \\ b=\dfrac{1}{8}\\ \\ a=\dfrac{1}{16}\end{cases}

Abbiamo così ottenuto come soluzioni del sistema di partenza due terne di valori {a,b,c}, a ciascuna delle quali corrisponde un’equazione di una parabola, tale da soddisfare le condizioni di partenza del problema. E ciascuna equazione si ottiene sostituendo all’equazione della parabola in forma generale {y=ax^2+bx+c} i valori dei coefficienti {a,b,c} corrispondenti a ciascuna terna soluzione del sistema.

Così, le due parabole aventi asse di simmetria {x=-1}, direttrice {y=-\dfrac{29}{4}} e passanti per il punto {P_1=(1,-3)} sono in conclusione:

\mathscr{P_1}: y=x^2+2x-6; \qquad \mathscr{P}_2: y=\dfrac{1}{16}x^2+\dfrac{1}{8}x-\dfrac{51}{16}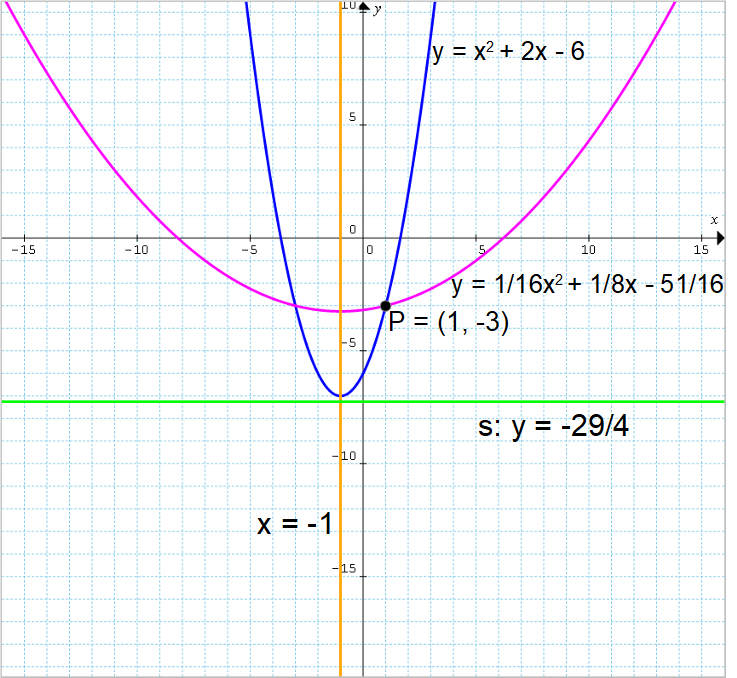

Metodo della ricerca delle coordinate del fuoco: parabola con asse verticale

Consideriamo ancora una parabola con asse verticale della quale siano note le equazioni della direttrice e dell’asse e le coordinate di un punto appartenente alla parabola stessa.

Il metodo che illustreremo ora consiste nel ricercare le coordinate del fuoco della parabola. E per la verità, poiché il fuoco di una parabola appartiene all’asse di simmetria, l’ascissa del fuoco stesso è nota. Infatti, se l’asse della parabola ha equazione:

x=h

l’ascissa del fuoco sarà di conseguenza:

x_F=h

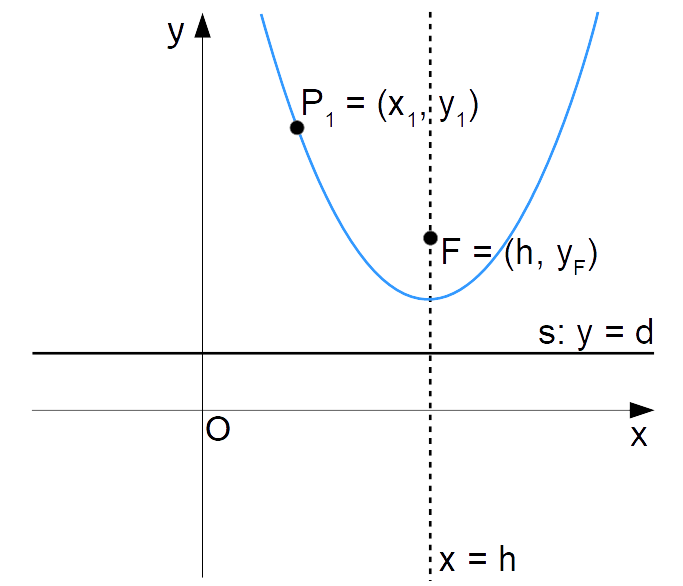
Per determinare l’ordinata del fuoco {y_F} possiamo procedere utilizzando la definizione di parabola con asse verticale come luogo geometrico, utilizzando le coordinate del punto {P_1} e la distanza con segno {d} della direttrice rispetto all’asse delle {x}:

(x_F-x_1)^2+(y_F-y_1)^2=(y_1-d)^2

Come è immediato verificare, l’unica incognita presente nell’equazione è {y_F}, ovvero l’ordinata del fuoco. Di conseguenza, sostituendo i valori si ottiene un’equazione nella sola incognita {y_F} che, risolta, fornisce il valore o i valori dell’ordinata del fuoco. Osserviamo che se si ottengono due valori per tale ordinata, ciò significa che abbiamo due parabole tali da rispettare le condizioni imposte dal problema.

A tal punto, disponendo delle coordinate del fuoco e della distanza con segno {d}, è possibile scrivere l’equazione della parabola sfruttando ancora la definizione di parabola come luogo geometrico, considerando però in questo caso un generico punto {P=(x,y)} appartenente alla parabola:

(x_F-x)^2+(y_F-y)^2=(y-d)^2

Rivediamo l’esempio precedente utilizzando questo metodo alternativo.

Esempio 1 bis

Determinare l’equazione di una parabola o delle parabole tali da avere asse di simmetria di equazione {x=-1}, direttrice di equazione {y=-\dfrac{29}{4}} e tali da passare per il punto {P_1=(1,-3)}. Utilizzare il metodo basato sulla ricerca delle coordinate del fuoco.

Poiché l’asse della parabola ha equazione:

x=-1

l’ascissa del fuoco {x_F} sarà proprio uguale a {-1}. Infatti, il fuoco appartiene all’asse di simmetria della parabola.

Inoltre, viste le coordinate del punto {P_1} e l’equazione della direttrice della parabola si ha:

x_1=1; \quad y_1=-3; \quad d=-\dfrac{29}{4}

Per determinare l’ordinata del fuoco {y_F}, si tratterà di risolvere l’equazione:

(x_F-x_1)^2+(y_F-y_1)^2=(y_1-d)^2

ovvero sostituendo i valori:

(-1-1)^2+[y_F-(-3)]^2=\left[-3-\left( -\dfrac{29}{4}\right)\right]^2

Sviluppiamo i calcoli:

\begin{align*} &(-2)^2+(y_F+3)^2=\left( -3+\dfrac{29}{4}\right)^2; \\ \\ & 4+y_F^2+6y_F+9=\left( \dfrac{-12+29}{4}\right)^2;\\ \\ & y_F^2+6y_F+13-\left( \dfrac{17}{4}\right)^2=0;\\ \\ & y_F^2+6y_F-\dfrac{81}{16}=0\end{align*}

Risolviamo l’equazione di secondo grado, che si presenta nella sola incognita {y_F}:

\begin{align*} &y_{F_{1,2}}=-3 \pm \sqrt{9+\dfrac{81}{16}}=-3 \pm \sqrt{\dfrac{144+81}{16}}=\\ \\ & =-3 \pm \sqrt{\dfrac{225}{16}}=-3 \pm \dfrac{15}{4}=\dfrac{-12\pm 15}{4}=\begin{cases} \dfrac{3}{4} \\ \\ -\dfrac{27}{4}\end{cases}\end{align*}

Abbiamo ottenuto due valori per l’ordinata del fuoco. Ciò significa che le parabole che soddisfano le condizioni date dal problema sono due. Entrambe le parabole hanno fuochi caratterizzati dalla stessa ascissa. Le ordinate dei fuochi sono invece differenti.

Cominciamo applicando la definizione come luogo geometrico relativamente alla prima parabola, avente fuoco {F=\left( -1, \dfrac{3}{4}\right)} e distanza con segno {d} uguale a {-\dfrac{29}{4}}. Consideriamo un generico punto della parabola di coordinate {x} e {y}:

(x_F-x)^2+(y_F-y)^2=(y-d)^2

ovvero, sostituendo i valori:

(-1-x)^2+\left( \dfrac{3}{4}-y\right)^2=\left( y+\dfrac{29}{4}\right)^2

Sviluppando i quadrati:

\begin{align*} &1+2x+x^2+\dfrac{9}{16}-\dfrac{3}{2}y+\cancel{y^2}=\cancel{y^2}+\dfrac{29}{2}y+\dfrac{841}{16};\\ \\ & \left( \dfrac{29}{2}+\dfrac{3}{2}\right)y=x^2+2x+1+\dfrac{9}{16}-\dfrac{841}{16};\\ \\ & 16y=x^2+2x+\dfrac{16+9-841}{16};\\ \\ & 16y=x^2+2x-51;\\ \\ & \mathscr{P}_1: y=\dfrac{1}{16}x^2+\dfrac{1}{8}x-\dfrac{51}{16}\end{align*}

Veniamo ora alla seconda parabola, avente ordinata del fuoco {y_F=-\dfrac{27}{4}} e avente ascissa del fuoco e distanza {d} come la prima parabola:

\begin{align*} &(x_F-x)^2+(y_F-y)^2=(y-d)^2; \\ \\ & (-1-x)^2+\left( -\dfrac{27}{4}-y\right)^2=\left(y+\dfrac{29}{4}\right)^2;\\ \\ & 1+2x+x^2+\dfrac{729}{16}+\dfrac{27}{2}y+\cancel{y^2}=\cancel{y^2}+\dfrac{29}{2}y+\dfrac{841}{16};\\ \\ & \left( \dfrac{29}{2}-\dfrac{27}{2}\right)y=x^2+2x+1+\dfrac{729}{16}-\dfrac{841}{16};\\ \\ & y=x^2+2x+\dfrac{16+729-841}{16};\\ \\ & \mathscr{P}_2: y=x^2+2x-6\end{align*}

Come è immediato osservare, abbiamo ritrovato correttamente le stesse equazioni delle parabole determinate nell’esempio precedente.

Metodo del sistema: parabola con asse orizzontale

Consideriamo una parabola con asse orizzontale, avente equazione in forma generica:

x=ay^2+by+c, \qquad a \neq 0, \quad a,b,c \in \R

Come nei casi precedenti, disponiamo delle coordinate di un punto appartenente alla parabola e delle equazioni dell’asse di simmetria e della direttrice:

P_1=(x_1, y_1); \qquad \underbrace{y=h}_{\text{asse}}; \qquad \underbrace{s:x=d}_{\text{direttrice}}

In modo del tutto simile a quanto visto per le parabole con asse verticale, a partire dalle coordinate del punto {P_1} è possibile scrivere la condizione di appartenenza:

ay_1^2+by_1+c=x_1

Inoltre, poiché il fuoco della parabola appartiene all’asse di simmetria, per l’ordinata del fuoco {y_F} si ha:

\overbrace{-\dfrac{b}{2a}}^{y_F}=h

Infine, ricordando l’espressione in funzione dei coefficienti {a,b,c} della distanza con segno {d} relativa ad una parabola con asse orizzontale, possiamo scrivere:

-\dfrac{1+\Delta}{4a}=d

Mettendo a sistema le ultime tre uguaglianze scritte abbiamo quindi:

\begin{cases}ay_1^2+by_1+c=x_1 \\ \\  -\dfrac{b}{2a}=h  \\ \\ -\dfrac{1+\Delta}{4a}=d\end{cases}

ovvero ricordando che {\Delta = b^2-4ac}:

\begin{cases} ay_1^2+by_1+c=x_1 \\ \\ -\dfrac{b}{2a}=h \\ \\ \dfrac{4ac-1-b^2}{4a}=d\end{cases} \quad \small \text{parabola con asse orizzontale}

Risolvendo il sistema è possibile determinare i valori dei coefficienti {a,b,c}, grazie ai quali è possibile scrivere l’equazione o le equazioni delle parabole che rispettano le condizioni date.

Il sistema appena scritto è molto simile a quello relativo ad una parabola con asse verticale. L’unica differenza è data dalla prima equazione a sistema.

Esempio 2

Determinare l’equazione o le equazioni delle parabole aventi asse di simmetria {y=-\dfrac{3}{2}}, direttrice {x=-\dfrac{7}{2}} e passanti per il punto {P_1=(3,1)}.

In base ai dati forniti dal problema abbiamo {h=-\dfrac{3}{2}}, {d=-\dfrac{7}{2}}, {x_1=3} e {y_1=1}.

Poiché l’asse della parabola è una retta orizzontale, ovvero è una retta della forma {y=h}, concludiamo immediatamente che la parabola che stiamo ricercando è ad asse orizzontale (una o due parabole). Di conseguenza, dovremo considerare il sistema:

\begin{cases} ay_1^2+by_1+c=x_1 \\ \\ -\dfrac{b}{2a}=h \\ \\ \dfrac{4ac-1-b^2}{4a}=d\end{cases}

ovvero, sostituendo i valori relativi al problema in esame:

\begin{cases} a+b+c=3 \\ \\ -\dfrac{b}{2a}=-\dfrac{3}{2} \\ \\ \dfrac{4ac-1-b^2}{4a}=-\dfrac{7}{2}\end{cases}

Per risolvere il sistema, procediamo allo stesso modo visto negli esempi precedenti. In particolare, cominciamo ricavando un’espressione per {b} dalla seconda equazione:

\begin{cases} a+b+c=3 \\ \\ -\dfrac{b}{2a}=-\dfrac{3}{2} \quad \rightarrow \quad b=\dfrac{3}{2}\cdot2a \quad \rightarrow \quad b=3a, \quad (a \neq0) \\ \\ \dfrac{4ac-1-b^2}{4a}=-\dfrac{7}{2}\end{cases}

Ora sostituiamo l’espressione appena ottenuta per {b} nelle rimanenti equazioni a sistema:

\begin{cases} a+3a+c=3 \quad \rightarrow \quad 4a+c=3 \\ \\  b=3a \\ \\ \dfrac{4ac-1-9a^2}{4a}=-\dfrac{7}{2}\end{cases}

A questo punto non resta che ricavare un’espressione per {c} dalla prima equazione e sostituirla nella terza equazione. In tal modo, la terza equazione avrà come incognita soltanto {a}:

\begin{cases} 4a+c=3 \quad \rightarrow \quad c=3-4a \\ \\  b=3a \\ \\ \dfrac{4a\cdot (3-4a)-1-9a^2}{4a}=-\dfrac{7}{2}\end{cases}

Adesso lavoriamo soltanto sulla terza equazione, in modo da ricavare il valore o i valori corrispondenti al coefficiente {a}:

\begin{align*} &\dfrac{4a\cdot (3-4a)-1-9a^2}{4a}=-\dfrac{7}{2}; \\ \\ & \dfrac{12a-16a^2-1-9a^2}{4a}+\dfrac{7}{2}=0; \\ \\ & \dfrac{12a-16a^2-1-9a^2+14a}{\cancel{4a}}=0, \qquad (a \neq 0); \\ \\ & -25a^2+26a-1=0;\\ \\ & 25a^2-26a+1=0\\ \\ \end{align*}

Risolvendo l’equazione di secondo grado ottenuta abbiamo:

\begin{align*} &a_{1,2}=\dfrac{13 \pm \sqrt{169-25}}{25}=\dfrac{13 \pm 12 }{25}=\begin{cases} 1 \\ \\ \dfrac{1}{25}\end{cases}\end{align*}

Il sistema può essere così riscritto come:

\begin{cases}  c=3-4a \\ \\  b=3a \\ \\a=1 \quad \vee \quad a=\dfrac{1}{25}\end{cases}

ovvero:

\begin{cases}  c=3-4a \\ \\  b=3a \\ \\a=1 \end{cases} \qquad \vee \qquad \begin{cases} c=3-4a \\ \\ b=3a \\ \\ a=\dfrac{1}{25}\end{cases}

Risolvendo ciascun sistema otteniamo due terne di soluzioni per il sistema di partenza:

\begin{cases} c=-1\\ \\ b=3 \\ \\ a = 1\end{cases} \qquad \vee \qquad \begin{cases} c=\dfrac{71}{25} \\ \\ b=\dfrac{3}{25}\\ \\ a=\dfrac{1}{25}\end{cases}

A ciascuna terna corrisponde una parabola che rispetta le condizioni imposte dal problema. In particolare, sostituendo i valori ricavati per i coefficienti {a,b,c} nell’equazione di una generica parabola con asse orizzontale, ovvero nell’equazione {x=ay^2+by+c}, otteniamo considerando ciascuna terna di valori le due parabole aventi equazioni:

\mathscr{P}_1: x=y^2+3y-1; \qquad \mathscr{P}_2: x=\dfrac{1}{25}y^2+\dfrac{3}{25}y+\dfrac{71}{25}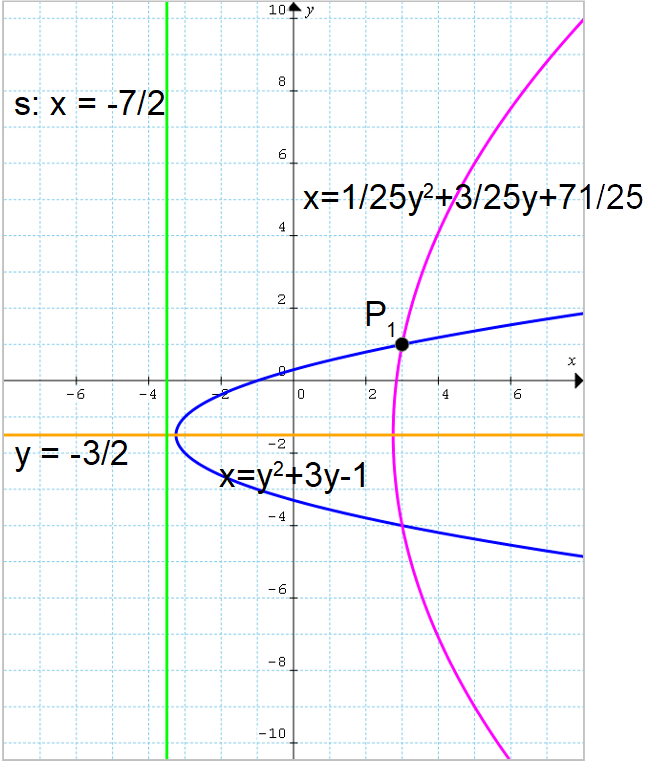

Metodo della ricerca delle coordinate del fuoco: parabola con asse orizzontale

Consideriamo ancora una parabola con asse orizzontale della quale siano note le equazioni della direttrice e dell’asse di simmetria, nonché le coordinate di un punto {P_1} ad essa appartenente. Ancora, il nostro obiettivo è determinare l’equazione della parabola o delle parabole corrispondenti, stavolta ricercando le coordinate del fuoco.

Poiché la parabola ha asse orizzontale, l’ordinata del suo fuoco è già nota. Se infatti l’asse della parabola ha equazione del tipo:

y=h

l’ordinata del fuoco {y_F} sarà proprio {h}.

Rimane invece da determinare l’ascissa del fuoco {x_F}, ma per fare ciò basta sfruttare la definizione di parabola come luogo geometrico, relativamente al punto {P_1}, il quale dovrà presentare la medesima distanza rispetto al fuoco della parabola e alla sua direttrice:

(x_F-x_1)^2+(y_F-y_1)^2=(x_1-d)^2

Attenzione ad utilizzare correttamente la definizione come luogo geometrico di una parabola con asse orizzontale (vedi secondo membro dell’equazione appena scritta).

Sostituendo i valori si ottiene un’equazione nella sola incognita {x_F}, grazie alla quale è possibile ricavare il valore o i valori dell’ascissa del fuoco. Osserviamo che se si ottengono più valori (due), ciò significa che avremo due parabole tali da rispettare i requisiti posti dal particolare problema in esame.

Note le coordinate del fuoco sarà infine possibile determinare l’equazione o le equazioni delle parabole, sfruttando ancora la definizione di parabola come luogo geometrico, tuttavia relativamente ad un generico punto della parabola stessa, avente coordinate {x} e {y}:

(x_F-x)^2+(y_F-y)^2=(x-d)^2

Rivediamo il precedente esempio utilizzando questo metodo alternativo.

Esempio 2 bis

Determinare l’equazione o le equazioni delle parabole aventi asse di simmetria {y=-\dfrac{3}{2}}, direttrice {x=-\dfrac{7}{2}} e passanti per il punto {P_1=(3,1)}. Utilizzare il metodo della ricerca delle coordinate del fuoco.

Dato che l’asse di simmetria è rappresentato da una retta orizzontale, la parabola ha asse orizzontale. Inoltre, il fuoco appartiene a tale asse ed ha quindi ordinata uguale a:

y_F=-\dfrac{3}{2}

Sfruttando la definizione di parabola con asse orizzontale come luogo geometrico, ricaviamo il valore dell’ascissa del fuoco {x_F}:

(x_F-x_1)^2+(y_F-y_1)^2=(x_1-d)^2

ovvero sostituendo i valori noti:

(x_F-3)^2+\left( -\dfrac{3}{2}-1\right)^2=\left( 3+\dfrac{7}{2}\right)^2

Svolgendo i calcoli abbiamo:

\begin{align*} &x_F^2-6x_F+9+\left( -\dfrac{5}{2}\right)^2=\left( \dfrac{6+7}{2}\right)^2; \\ \\ & x_F^2-6x_F+9+\dfrac{25}{4}-\dfrac{169}{4}=0;\\ \\ &x_F^2-6x_F+9-36=0;\\ \\ & x_F^2-6x_F-27=0 \end{align*}

Ora risolviamo l’equazione di secondo grado appena ottenuta, che si presenta nella sola incognita {x_F}:

\begin{align*} &x_{F_{1,2}}={3 \pm \sqrt{9-(-27)}}=3\pm 6 =\begin{cases} 9 \\ \\ -3\end{cases}\end{align*}

Le condizioni poste dal problema risultano dunque soddisfatte da due parabole, aventi entrambe ordinata del fuoco uguale a {-\dfrac{3}{2}} e ascissa del fuoco stesso rispettivamente {9} e {-3}.

Per la prima parabola abbiamo, applicando la definizione di parabola con asse orizzontale come luogo geometrico relativamente ad un generico punto della parabola:

\begin{align*} &(x_F-x)^2+(y_F-y)^2=(x-d)^2;\\ \\ & (9-x)^2+\left( -\dfrac{3}{2}-y\right)^2=\left( x+\dfrac{7}{2}\right)^2;\\ \\ & 81-18x+\cancel{x^2}+\dfrac{9}{4}+3y+y^2=\cancel{x^2}+7x+\dfrac{49}{4};\\ \\ &(7+18)x=y^2+3y+81+\dfrac{9}{4}-\dfrac{49}{4}=0;\\ \\ & 25x=y^2+3y+81-10=0;\\ \\ & \mathscr{P}_1:x=\dfrac{1}{25}y^2+\dfrac{3}{25}y+\dfrac{71}{25} \end{align*}

Allo stesso modo, per la seconda parabola si ha in conclusione:

\begin{align*} &(x_F-x)^2+(y_F-y)^2=(x-d)^2; \\ \\ & (-3-x)^2+\left( -\dfrac{3}{2}-y\right)^2=\left( x+\dfrac{7}{2}\right)^2;\\ \\ & 9+6x+\cancel{x^2}+\dfrac{9}{4}+3y+y^2=\cancel{x^2}+7x+\dfrac{49}{4};\\ \\ & (7-6)x=y^2+3y+9+\dfrac{9}{4}-\dfrac{49}{4};\\ \\ &\mathscr{P}_2: x=y^2+3y-1\end{align*}

Abbiamo correttamente ritrovato i risultati già ottenuti nell’esempio 2.

Conclusioni

Abbiamo visto come determinare l’equazione di una parabola (o di più di una parabola) note le equazioni dell’asse di simmetria e della direttrice e le coordinate di un punto appartenente alla parabola stessa. Qui si conclude il ciclo di lezioni dedicato alle condizioni per determinare l’equazione di una parabola. Nella prossima lezione ci occuperemo di un’interessante proprietà ottica del fuoco di una parabola. Vi consigliamo inoltre la lettura della risposta relativa alle parabole congruenti o sovrapponibili.

Un saluto a tutti voi e, come sempre, buono studio con SìMatematica!