Parabole congruenti o sovrapponibili

 - 

Domande e risposte

Quando due parabole sono congruenti o sovrapponibili? Quale è la loro definizione? Inoltre, quale è la condizione per la quale due parabole possono dirsi congruenti o sovrapponibili? Infine, potreste fare degli esempi sulle parabole congruenti?

Due parabole si dicono sovrapponibili (o congruenti) se queste possono essere sovrapposte mediante un movimento rigido, ovvero mediante traslazioni, rotazioni e simmetrie (isometrie). In particolare, due parabole risultano sovrapposte quando tutti i punti di una parabola coincidono con tutti i punti dell’altra.

Parabole congruenti: caso di una parabola con vertice nell’origine e di una parabola con vertice qualsiasi

Supponiamo di avere una parabola con asse verticale e con vertice nell’origine degli assi:

\mathscr{P}:y=ax^2, \qquad a \neq0, \quad a\in \R

Consideriamo anche una generica parabola con asse verticale:

\mathscr{P}': y=ax^2+bx+c, \qquad a \neq0, \quad a,b,c \in \R

Sul piano cartesiano abbiamo una situazione del tipo la seguente:

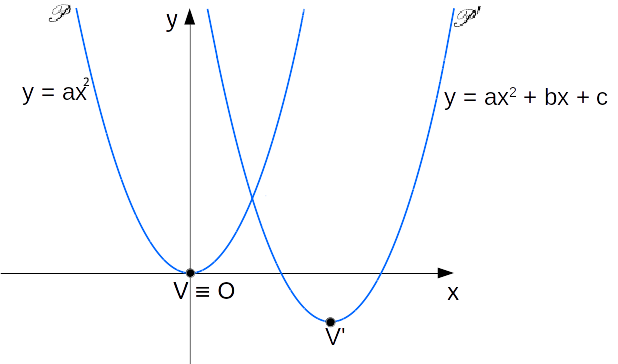
E’ importante far caso che le equazioni delle due parabole condividono lo stesso valore del coefficiente del termine di secondo grado, ovvero del coefficiente a. Ora, ci domandiamo se sotto tale ipotesi due parabole sono in generale sovrapponibili.

Osserviamo anzitutto che la parabola {\mathscr{P}} ha vertice {V=(0,0)}, mentre la parabola {\mathscr{P}'} ha vertice di coordinate:

V'=\left(-\dfrac{b}{2a}, -\dfrac{\Delta}{4a} \right)

Ciò deriva dalle formule per le coordinate del vertice di una parabola con asse verticale viste a suo tempo.

Così, se vogliamo passare dal vertice V al vertice V' dobbiamo operare una certa trasformazione, in particolare una traslazione, che consiste nel sommare all’ascissa del vertice {V} la quantità -\dfrac{b}{2a} e all’ordinata dello stesso vertice la quantità -\dfrac{\Delta}{4a}. Più tecnicamente, diciamo che operiamo una traslazione di vettore \boldsymbol{v}=\left(-\dfrac{b}{2a}, -\dfrac{\Delta}{4a}\right).

Ora, ci domandiamo se tale traslazione, che trasforma il vertice V in V', trasforma anche in generale un qualunque punto della parabola \mathscr{P} nel corrispondente punto della parabola \mathscr{P}'. Se così fosse, le due parabole risulterebbero congruenti o sovrapponibili. Infatti, esisterebbe in tal caso un’isometria in grado di far coincidere tutti i punti di una parabola con tutti i punti dell’altra.

Per effettuare tale verifica, occorre considerare la trasformazione geometrica che intendiamo operare e quindi applicarla all’equazione della parabola \mathscr{P}. Se con tale trasformazione a partire dall’equazione di \mathscr{P} otterremo l’equazione di \mathscr{P}' e viceversa, potremo dire che le due parabole sono congruenti o sovrapponibili.

In particolare, indicato con P=(x,y) il punto da trasformare e con P'=(x', y') il punto trasformato, la trasformazione T che intendiamo operare è la traslazione:

T:\begin{cases}{}x'= x -  \dfrac{b}{2a}; \\ \\ y'=y-\dfrac{\Delta}{4a} \end{cases}

Ribaltando ciascuna formula a sistema, le coordinate del punto di partenza a partire dalle coordinate del punto trasformato sono date da (trasformazione inversa):

T^{-1}:\begin{cases} x=x'+\dfrac{b}{2a}; \\ \\  y=y'+\dfrac{\Delta}{4a} \end{cases}

Così, tenendo conto delle ultime uguaglianze scritte ovvero operando la trasformazione {T^{-1}}, l’equazione della parabola \mathscr{P}, ossia:

\mathscr{P}: y=ax^2

diviene, sostituendo ad x e y le corrispondenti espressioni:

\overbrace{y'+\dfrac{\Delta}{4a}}^{y}=a \bigg(\overbrace{x'+\dfrac{b}{2a} }^{x}\bigg)^{2}

ovvero, tenendo conto che \Delta = b^2-4ac e svolgendo i calcoli (sotto l’ipotesi {a \neq 0}):

\begin{align*}&y'+\dfrac{b^2-4ac}{4a}=a \left({x'}^2+\dfrac{bx'}{a}+\dfrac{b^2}{4a^2} \right); \\ \\ &y'+\cancel{\dfrac{b^2}{4a}}-c=a{x'}^2+bx'+\cancel{\dfrac{b^2}{4a} }; \\ \\ &\boxed{\mathscr{P}':y'=a{x'}^2+bx'+c}, \qquad (a \neq 0)\end{align*}

Otteniamo così l’equazione della parabola {\mathscr{P}'}. Osserviamo che la presenza degli apici indica soltanto che abbiamo operato una trasformazione, ma ci ritroviamo comunque di fronte all’equazione della parabola {\mathscr{P}}.

Vediamo quindi che a partire dall’equazione della parabola {\mathscr{P}}, operando la traslazione {T^{-1}} ritroviamo l’equazione della parabola {\mathscr{P}'}. Ciò significa che è possibile sovrapporre la parabola {\mathscr{P}} alla parabola {\mathscr{P}'}.

Allo stesso modo, dall’equazione di \mathscr{P}' (da considerare per non fare confusione nella forma con gli apici) è possibile ricondursi all’equazione di \mathscr{P} mediante la trasformazione T. Infatti, sostituendo nell’equazione di {\mathscr{P}'} le espressioni per y' ed x' relative alla trasformazione {T}, si ha (passaggi validi per a diverso da zero):

\begin{align*}& \overbrace{y-\dfrac{\Delta}{4a}}^{y'}=a \cdot \bigg(\overbrace{x-\dfrac{b}{2a} }^{x'}\bigg)^2+b \cdot \bigg(\overbrace{x-\dfrac{b}{2a}}^{x'} \bigg)+c; \\ \\ & y-\dfrac{b^2}{4a}+\cancel{c}=a \cdot \left(x^2-\dfrac{bx}{a}+\dfrac{b^2}{4a^2} \right)+bx-\dfrac{b^2}{2a}+\cancel{c}; \\ \\ & y=ax^2-\cancel{bx}+\dfrac{b^2}{4a}+\cancel{bx}-\dfrac{b^2}{2a}+\dfrac{b^2}{4a}; \\ \\ &\dfrac{y}{4a}=\dfrac{4a^2x^2+\cancel{b^2}-\cancel{2b^2}+\cancel{b^2}}{4a}; \\ \\ & \boxed{\mathscr{P}:y=ax^2}, \qquad (a \neq 0)\end{align*}

Abbiamo quindi ritrovato, operando la trasformazione T, l’equazione della parabola di partenza. Quindi, anche la parabola {\mathscr{P}'} risulta sovrapponibile alla parabola {\mathscr{P}}. Pertanto, possiamo concludere che ciascuna parabola è sovrapponibile all’altra.

Di conseguenza, è possibile affermare che le due parabole \mathscr{P} e \mathscr{P}' sono congruenti o sovrapponibili, in quanto dall’equazione dell’una è possibile ottenere l’equazione dell’altra mediante una isometria (trasformazione data da un movimento rigido). Ed osserviamo che tali parabole hanno equazioni caratterizzate dallo stesso coefficiente a.

Si può dimostrare in generale che due parabole con equazioni aventi lo stesso coefficiente a sono sovrapponibili o congruenti. In più, come vedremo tra un istante due parabole sono sovrapponibili o congruenti se e solo se le rispettive equazioni presentano i coefficienti dei termini di secondo grado anche soltanto uguali in valore assoluto.

Pertanto, il nostro obiettivo è adesso quello di far vedere che due parabole con asse orizzontale e/o verticale sono sovrapponibili se presentano i coefficienti dei termini di secondo grado uguali tra loro almeno in valore assoluto (o modulo).

Parabole congruenti o sovrapponibili: un caso più generale

Ora, senza esaminare il caso più generale relativo a parabole con equazioni aventi coefficienti reali arbitrari, consideriamo per semplicità due parabole con equazioni aventi coefficienti noti, ad esempio:

\mathscr{P}:y=\dfrac{1}{16}x^2-\dfrac{1}{4}x+\dfrac{5}{4}; \qquad \mathscr{P}':x=-\dfrac{1}{16}y^2+\dfrac{3}{8}y+\dfrac{7}{16}

La prima parabola è ad asse verticale mentre la seconda è ad asse orizzontale. Inoltre, i coefficienti dei termini di primo grado e i termini noti che figurano nelle equazioni sono diversi tra loro. Tuttavia, le due parabole presentano equazioni nelle quali i coefficienti dei termini di secondo grado sono uguali in valore assoluto.

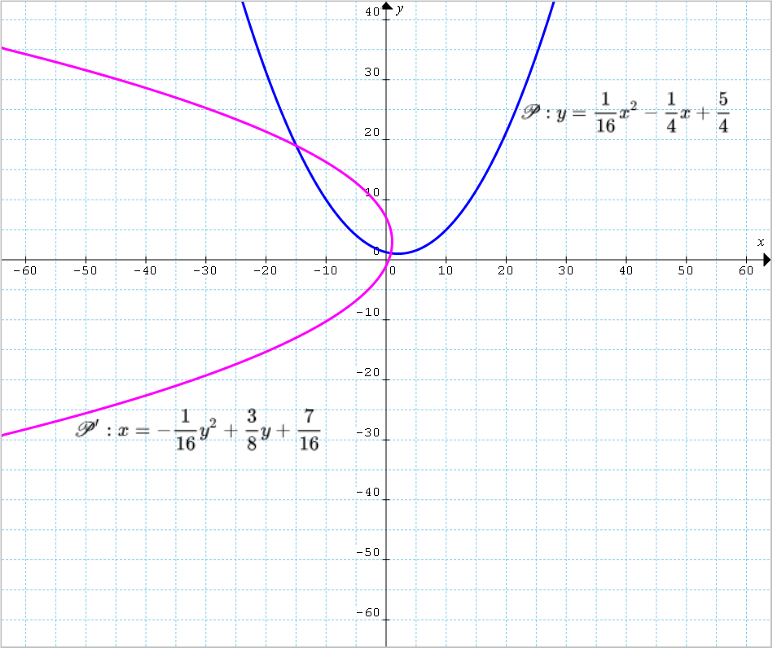
Se le due parabole sono sovrapponibili, mediante delle opportune isometrie sarà possibile passare dall’equazione della parabola {\mathscr{P}} all’equazione della parabola {\mathscr{P}'} e viceversa. Ma come possiamo vedere dalla figura, è effettivamente possibile sovrapporre la parabola {\mathscr{P}} alla parabola {\mathscr{P}'} mediante una rotazione antioraria rispetto al suo vertice seguita da un’opportuna traslazione.

Ora, una rotazione antioraria di 90 gradi rispetto ad un certo punto {(x_0, y_0)} si esprime in generale come:

T_r: \begin{cases} x'=-y+y_0+x_0 \\ \\ y'=x-x_0+y_0\end{cases} \qquad \small\text{rotazione antioraria di 90° rispetto a }(x_0, y_0)

Nel nostro caso, il punto rispetto al quale eseguire la rotazione dovrà essere il vertice {V} della parabola di partenza, ovvero il vertice della parabola {\mathscr{P}}.

Le coordinate del vertice {V} della parabola {\mathscr{P}} sono date da:

\small V=\left( -\dfrac{b}{2a}, -\dfrac{\Delta}{4a}\right)=\left( -\dfrac{-\frac{1}{4}}{\frac{1}{8}},-\dfrac{\frac{1}{16}-4 \cdot \frac{1}{16} \cdot \frac{5}{4}}{4 \cdot \frac{1}{16}}\right)=\left(2,\dfrac{1}{4} \cdot 4 \right)=(2,1)=(x_0, y_0)

Così, sostituendo i valori appena ottenuti, la rotazione che dobbiamo eseguire è esprimibile come:

\small T_r: \begin{cases} x'=-y+y_0+x_0 \\ \\ y'=x-x_0+y_0\end{cases} \quad \Rightarrow \quad  \begin{cases}x '= -y+1+2 \\ \\ y'=x-2+1 \end{cases} \quad \Rightarrow \quad \begin{cases} x'=-y+3 \\ \\ y'=x-1\end{cases}

Ora, per poter applicare la trasformazione appena scritta all’equazione della parabola {\mathscr{P}}, dobbiamo prima esplicitare le quantità {y} e {x} da ciascuna equazione a sistema. Si ha:

T_r^{-1}: \begin{cases}y=-x'+3 \\ \\x=y'+1\end{cases}

In questo modo otteniamo la trasformazione inversa di {T_r}, ovvero {T_r^{-1}}.

Sostituendo le espressioni così ottenute per {y} e {x} nell’equazione della parabola {\mathscr{P}} si ha:

\begin{align*} & \mathscr{P}:y=\dfrac{1}{16}x^2-\dfrac{1}{4}x+\dfrac{5}{4} \quad \stackrel{\large{T_r^{-1}}}{\Rightarrow} \\ \\& -x'+3=\dfrac{1}{16}\left( y'+1\right)^2-\dfrac{1}{4}(y'+1)+\dfrac{5}{4};\\ \\ & -x'=\dfrac{1}{16}(y'^2+2y'+1)-\dfrac{1}{4}y'-\dfrac{1}{4}+\dfrac{5}{4}-3;\\ \\ & -x'=\dfrac{1}{16}y'^2+\dfrac{1}{8}y'+\dfrac{1}{16}-\dfrac{1}{4}y'-\dfrac{1}{4}+\dfrac{5}{4}-3;\\ \\ & -x'=\dfrac{1}{16}y'^2+\left(\dfrac{1}{8}-\dfrac{1}{4} \right)y'+\dfrac{1}{16}-\dfrac{1}{4}+\dfrac{5}{4}-3;\\ \\ & -x'=\dfrac{1}{16}y'^2-\dfrac{1}{8}y'-\dfrac{31}{16}; \\ \\ & \mathscr{P}_{T_r^{-1}}:x'=-\dfrac{1}{16}y'^2+\dfrac{1}{8}y'+\dfrac{31}{16} \end{align*}

E quindi togliendo gli apici:

\mathscr{P}_{T_r^{-1}}: x=-\dfrac{1}{16}y^2+\dfrac{1}{8}y+\dfrac{31}{16}

Ora la parabola {\mathscr{P}} risulta ruotata di 90° in senso antiorario rispetto all’origine, ed effettivamente è diventata una parabola con asse orizzontale.

A questo punto, per arrivare all’equazione della parabola {\mathscr{P}'} dobbiamo utilizzare una traslazione in grado di trasformare il vertice {V_T \equiv V} della parabola {\mathscr{P}_{T_r^{-1}}} nel vertice {V'} della parabola {\mathscr{P}'.}

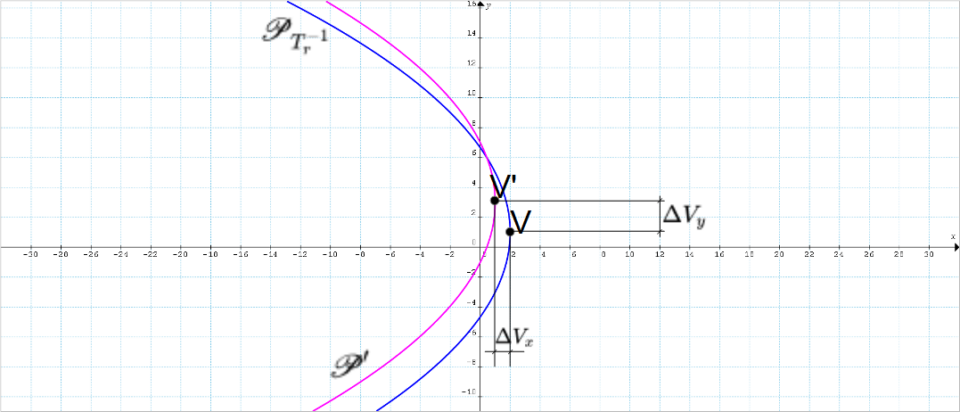
Cominciamo calcolando le coordinate dei vertici delle due parabole con le formule a noi note. Osserviamo che il calcolo delle coordinate del vertice della parabola {\mathscr{P}_{T_r^{-1}}} non è in realtà necessario, poiché questo coincide necessariamente con il vertice della parabola {\mathscr{P}} calcolato in precedenza. Tuttavia, riportiamo comunque a seguire il calcolo come esercizio. E’ invece necessario in ogni caso calcolare le coordinate del vertice {V'} della parabola {\mathscr{P}'}.

Così, indicato con {V_T} il vertice della parabola {\mathscr{P}_{T_r^{-1}}} e con {V'} il vertice della parabola {\mathscr{P}'} si ha:

\small\begin{align*} &V_T=\left( -\dfrac{\Delta}{4a}, -\dfrac{b}{2a}\right)=\left( -\dfrac{\frac{1}{64}+\frac{1}{4}\cdot \frac{31}{16}}{-\frac{1}{4}}, -\dfrac{\frac{1}{8}}{-\frac{1}{8}}\right)=\left( 2,1\right)=V=(x_V, y_V)\\ \\ & V'=\left( -\dfrac{\Delta}{4a}, -\dfrac{b}{2a}\right)=\left( -\dfrac{\frac{9}{64}+\frac{28}{16^2}}{-\frac{1}{4}},  -\dfrac{\frac{3}{8}}{-\frac{1}{8}},\right)=(1,3)=(x_{V'}, y_{V'})\end{align*}

Osserviamo che per semplicità abbiamo genericamente indicato i coefficienti dell’equazione di ciascuna parabola sempre con le lettere {a,b,c}, ma riesce inteso che in ciascun caso abbiamo preso i valori relativi all’opportuna equazione.

Ora, indichiamo le distanze positive prese lungo gli assi coordinati tra i vertici delle due parabole rispettivamente con {\Delta V_x} e {\Delta V_y} (vedi figura precedente). Si ha:

\Delta V_x =x_V-x_{V'}=2-1=1; \qquad \Delta V_y=y_{V'}-y_V=3-1=2

Così, riferendoci sempre al caso in figura, volendo passare dal vertice {V} al vertice {V'} dovremo considerare la traslazione:

T:\begin{cases} x'=x-\Delta V_x \\ \\ y'=y+\Delta V_y\end{cases}

ovvero, tenendo conto dei valori delle distanze {\Delta V_x} e {\Delta V_y}:

T:\begin{cases} x'=x-1 \\ \\ y'=y+2\end{cases}

A questo punto, in modo del tutto simile a quanto visto in precedenza, non resta che ribaltare le equazioni a sistema come segue:

T^{-1}: \begin{cases} x=x'+1 \\ \\ y=y'-2\end{cases}

e quindi sostituire le espressioni appena ottenute per {x} e {y} nell’equazione della parabola {\mathscr{P}_{T_r^{-1}}} (la parabola {\mathscr{P}} ruotata di 90° rispetto al suo vertice in senso antiorario). Abbiamo:

\begin{align*} &\mathscr{P}_{T_r^{-1}}: x=-\dfrac{1}{16}y^2+\dfrac{1}{8}y+\dfrac{31}{16} \quad \stackrel{\large T^{-1}}{\Rightarrow}\\ \\ & x'+1=-\dfrac{1}{16}\left( y'-2\right)^2+\dfrac{1}{8}\left( y'-2\right)+\dfrac{31}{16};\\ \\ & x'=-\dfrac{1}{16}\left( y'^2-4y'+4\right)+\dfrac{1}{8}y'-\dfrac{1}{4}+\dfrac{31}{16}-1; \\ \\ & x'=-\dfrac{1}{16}y'^2+\dfrac{1}{4}y'-\dfrac{1}{4}+\dfrac{1}{8}y'-\dfrac{1}{4}+\dfrac{31}{16}-1;\\ \\ &x'=-\dfrac{1}{16}y'^2+\left( \dfrac{1}{4}+\dfrac{1}{8}\right)y' +\dfrac{7}{16}; \\ \\ & x'=-\dfrac{1}{16}y'^2+\dfrac{3}{8}y'+\dfrac{7}{16}\end{align*}

Infine togliendo gli apici (ormai abbiamo eseguito la trasformazione):

  \boxed{\mathscr{P}':x=-\dfrac{1}{16}y^2+\dfrac{3}{8}y+\dfrac{7}{16}}

Abbiamo così ritrovato l’equazione della parabola {\mathscr{P}'}. Ciò significa che è possibile sovrapporre la parabola {\mathscr{P}} alla parabola {\mathscr{P}'} mediante delle isometrie (in questo caso, una rotazione antioraria rispetto ad un punto e una traslazione).

E’ inoltre possibile dimostrare in modo piuttosto simile che anche la parabola {\mathscr{P}'} è sovrapponibile alla parabola {\mathscr{P}} (omettiamo per brevità i relativi passaggi).

Quindi, in conclusione, le due parabole {\mathscr{P}} e {\mathscr{P}'} sono congruenti o sovrapponibili. E le rispettive equazioni hanno i coefficienti di secondo grado uguali in valore assoluto.

In generale, in accordo con quanto visto nel caso appena esaminato, è possibile dimostrare l’enunciato seguente.

Due parabole ciascuna con asse verticale od orizzontale sono congruenti o sovrapponibili se e solo se i coefficienti dei termini di secondo grado relativi alle rispettive equazioni, ovvero i rispettivi coefficienti {a}, sono uguali tra loro almeno in valore assoluto.

Vediamo ora degli esempi che mostrano come stabilire se due parabole sono congruenti o sovrapponibili oppure no.

Esempi

Esempio 1

Stabilire se la parabola {\mathscr{P}:y=3x^2+5x+7} e la parabola {\mathscr{P}:y=-3x^2-4x+5} sono congruenti o sovrapponibili.

Il coefficiente del termine di secondo grado relativo all’equazione della prima parabola è {3}, mentre il coefficiente del termine di secondo grado relativo all’equazione della seconda parabola è {-3}. I due coefficienti sono diversi tra loro ma uguali in valore assoluto. Di conseguenza, le due parabole risultano congruenti o sovrapponibili.

Esempio 2

Le parabole {\mathscr{P}: y= 5x^2-3x+4} e {\mathscr{P}': x=5y^2+6y-9} sono congruenti/sovrapponibili?

Osserviamo che le equazioni delle due parabole presentano lo stesso valore per il coefficiente del termine di secondo grado. La prima parabola è ad asse verticale, mentre la seconda è ad asse orizzontale, tuttavia la condizione per la congruenza di due parabole considera indifferentemente parabole con asse verticale e/o orizzontale. Di conseguenza, le due parabole in esame sono congruenti o sovrapponibili.

Esempio 3

La parabola {\mathscr{P}: y=-3x^2+4x-7} è congruente alla parabola {\mathscr{P}': x=3y^2+5x-6}?

Le equazioni relative alle due parabole presentano i coefficienti dei termini di secondo grado uguali tra loro in valore assoluto. Inoltre, come già sottolineato nell’esempio precedente, le parabole possono essere indifferentemente ad asse orizzontale o verticale. Di conseguenza, anche in questo caso le due parabole risultano congruenti o sovrapponibili.

Esempio 4

Verificare che le due parabole {\mathscr{P}:y=5x^2+3x+7} e {\mathscr{P}':x=7x^2+3x+7} non sono sovrapponibili.

Le due parabole non sono sovrapponibili poiché i coefficienti dei termini di secondo grado delle rispettive equazioni sono diversi tra loro anche in valore assoluto. Poco importa se i rimanenti coefficienti che figurano nelle equazioni sono tra loro uguali.

Una riflessione sul significato del coefficiente a nell’equazione della parabola

Abbiamo già visto a suo tempo come il segno del coefficiente {a} del termine di secondo grado dell’equazione di una parabola (con asse verticale od orizzontale) determini la concavità della parabola stessa.

Ora, il modulo del coefficiente {a} determina invece l’apertura della parabola. In particolare, più grande è il modulo del coefficiente {a} e minore sarà l’apertura della parabola. Viceversa, più piccolo è il modulo del coefficiente {a} e maggiore sarà l’apertura della parabola.

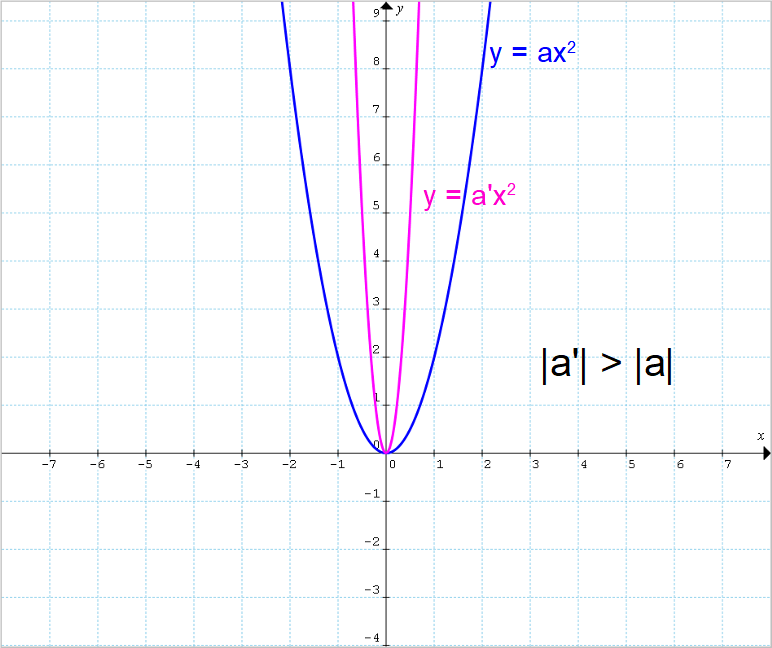
Così, data la definizione di apertura di una parabola, possiamo affermare in conclusione che due parabole con asse verticale e/o orizzontale sono congruenti se e solo se queste hanno la stessa apertura.