Il fuoco di una parabola presenta un’interessante proprietà ottica: un raggio di luce che emesso dal fuoco va ad incidere su un punto della parabola verrà riflesso in direzione parallela all’asse della parabola stessa. Viceversa, un raggio di luce che incide sulla parabola in direzione parallela all’asse della stessa viene riflesso sul fuoco.
Tale proprietà è molto importante per le pratiche applicazioni. Ad esempio, grazie ad uno specchio a forma di paraboloide di rivoluzione (superficie che si ottiene facendo ruotare una parabola attorno al proprio asse) è possibile riflettere la luce secondo una determinata direzione. Inoltre, utilizzando un particolare ricevitore a forma di paraboloide di rivoluzione è possibile captare le onde delle trasmissioni televisive, facendole concentrare in un determinato punto che effettivamente coincide con il fuoco del paraboloide. Ci riferiamo, come ovvio, alla parabola che viene utilizzata per la ricezione delle trasmissioni satellitari.
Prima di vedere nel dettaglio questa proprietà ottica del fuoco di una parabola, analizzeremo una proprietà geometrica che si servirà per le dimostrazioni successive. In particolare, mostreremo che la retta tangente ad una parabola in un dato punto {P} della parabola stessa è la bisettrice di un determinato angolo.
Ma vediamo gradualmente tutti i passaggi necessari per poter arrivare a definire questa particolare proprietà ottica del fuoco di una parabola.
Una proprietà ottica della parabola
Tangente ad una parabola in un suo punto come bisettrice di un particolare angolo
Consideriamo una parabola {\mathscr{P}} con asse ad esempio verticale e la retta {t} tangente alla parabola stessa nel punto {P}. Indichiamo con {F} il fuoco della parabola e con {s} la sua direttrice.
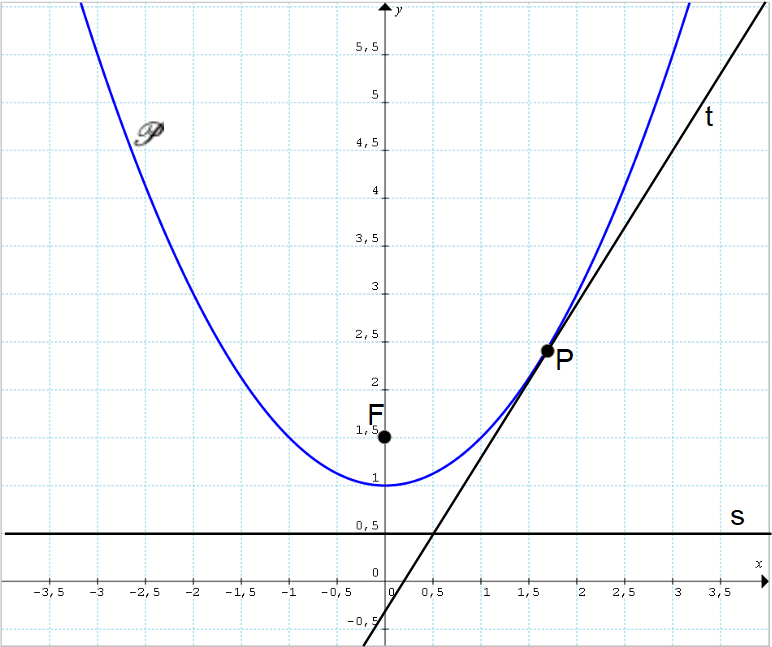
Osserviamo che nel particolare caso in figura l’asse della parabola coincide con l’asse {y}. Tuttavia, i discorsi che faremo a seguire sono validi anche nel caso in cui l’asse della parabola non coincida con l’asse {y}.
A questo punto tracciamo la retta {r} perpendicolare a {s} e passante per il punto {P}. Tale retta incontra la direttrice {s} della parabola nel punto {H}.
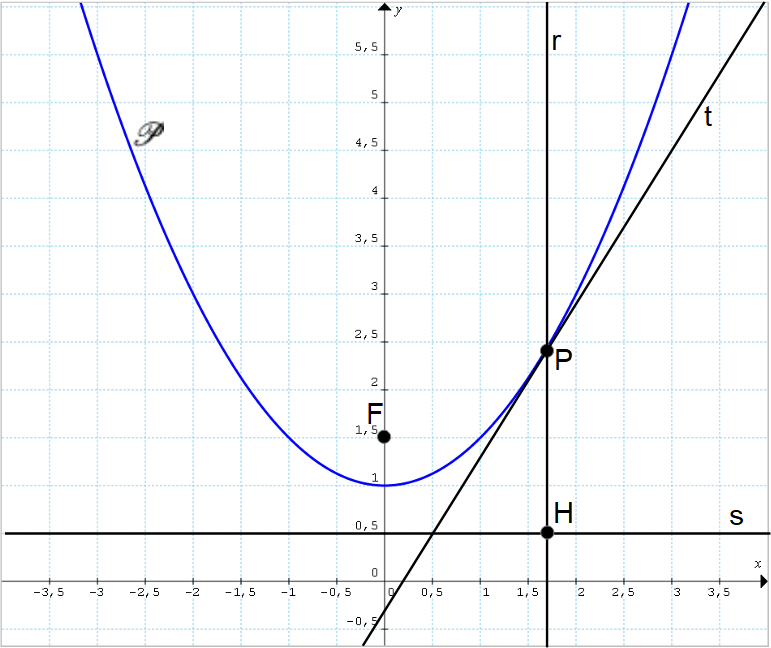
Per la definizione di parabola come luogo geometrico, poiché il punto {P} appartiene alla parabola, la distanza tra il punto {P} e il fuoco {F} è uguale alla distanza tra lo stesso punto {P} e la direttrice {s}:
\overline{PF}=\overline{PH}Se dunque consideriamo il triangolo {\stackrel{\triangle}{PFH}} e prendiamo come base {\overline{FH}}, esso risulterà isoscele.
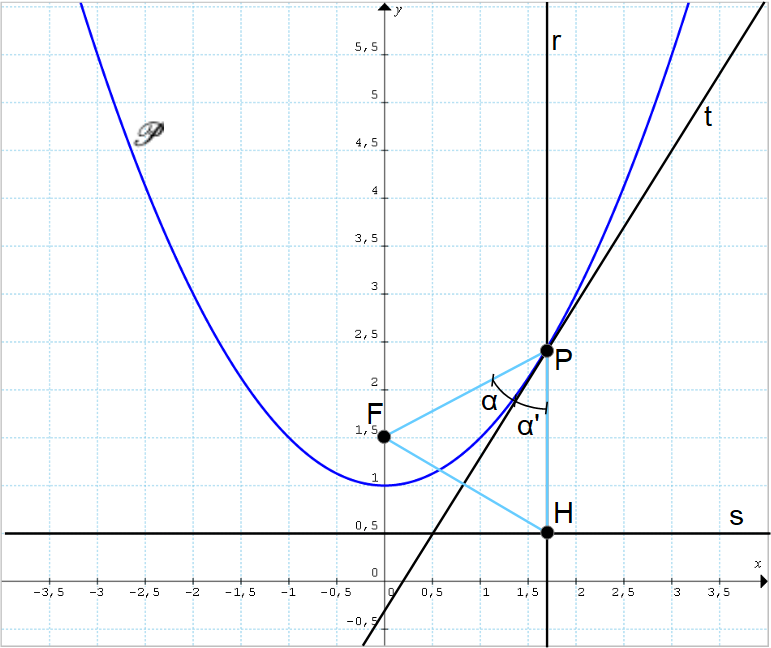
Ma se detto triangolo è isoscele, gli angoli {\alpha} ed {\alpha'} indicati in figura sono necessariamente uguali tra loro. Di conseguenza, è intuibile che la retta tangente {t} è la bisettrice interna dell’angolo {\stackrel{\angle}{PFH}}, ovvero l’angolo con vertice in {P} ed avente per lati le rette passanti rispettivamente per le coppie di punti {P, F} e {P, H}.
Per dimostrare che la retta {t} effettivamente coincide con la bisettrice dell’angolo {\stackrel{\angle}{PFH}}, l’idea è quella di provare che il punto {P} è l’unico punto della retta {t} tale da appartenere alla parabola.
Vediamo allora cosa succede prendendo un qualsiasi punto {Q} appartenente alla retta {t} e diverso da {P}.
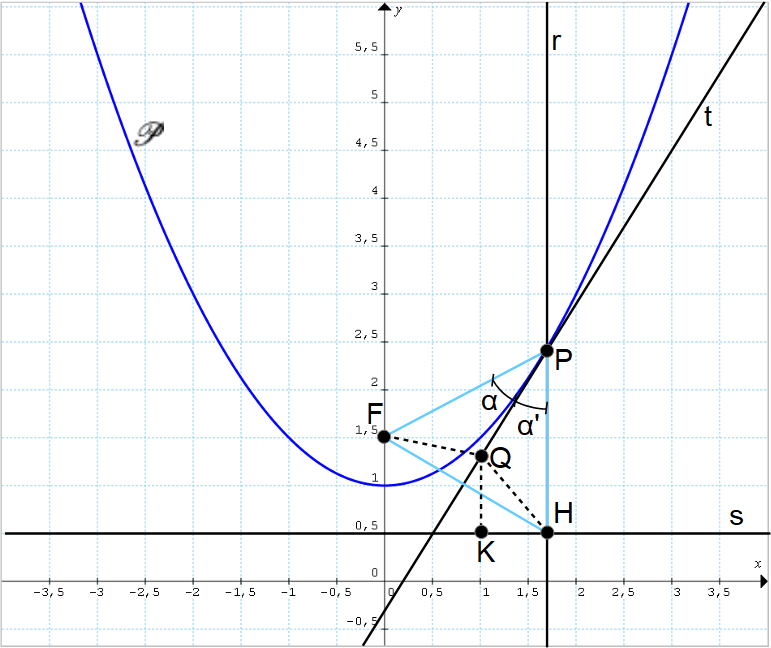
Affinché il punto {Q} appartenga alla parabola, questo deve presentare la stessa distanza rispetto al fuoco {F} e rispetto alla direttrice {s}. Ma, come dimostreremo tra un istante, la distanza {\overline{QF}} è diversa da {\overline{QK}}.
Osserviamo che le distanze {\overline{QF}} e {\overline{QH}} sono tra loro uguali, poiché {Q} appartiene alla bisettrice dell’angolo {\stackrel{\angle}{PFH}} (per definizione, ciascun punto della bisettrice di un angolo è equidistante dai lati dell’angolo stesso).
Ora, come è evidente dalla figura si ha {\overline{QH} > \overline{QK}}, e poiché le distanze {\overline{QF}} e {\overline{QH}} sono tra loro uguali, si ha necessariamente {\overline{QF} > \overline{QK}}. Di conseguenza, non avendosi l’uguaglianza {\overline{QF} = \overline{QK}} ogni punto {Q} di {t} diverso da {P} non può appartenere alla parabola {\mathscr{P}}. Per cui, la tangente {t} alla parabola nel punto {P} effettivamente coincide con la bisettrice interna dell’angolo {\stackrel{\angle}{PFH}}.
Vale dunque il seguente teorema.
Teorema. Consideriamo un punto {P} appartenente ad una parabola {\mathscr{P}}. Indichiamo con {F} il fuoco della parabola, con {s} la direttrice e con {H} il punto dato dall’intersezione della direttrice della parabola con la retta perpendicolare alla direttrice e passante per {P}. Sia inoltre {\stackrel{\angle}{PFH}} l’angolo avente per lati le rette passanti rispettivamente per le coppie di punti {P, F} e {P, H}.
Sotto tali ipotesi, la retta tangente {t} alla parabola nel punto {P} coincide con la bisettrice interna dell’angolo {\stackrel{\angle}{PFH}}.
Del teorema abbiamo già fornito la dimostrazione.
Podaria del fuoco rispetto alla parabola
Vogliamo ora presentare una ulteriore proprietà geometrica ed inoltre una particolare definizione (quella di “piede”) che ci saranno utili per dimostrare la proprietà ottica del fuoco di una parabola oggetto della lezione.
Ora, tra tutte le possibili rette tangenti ad una parabola in un suo punto, è opportuna una particolare riflessione relativa alla retta tangente alla parabola nel suo vertice. Il discorso è valido indifferentemente per parabole con asse orizzontale o verticale.
Riferendoci al caso delle precedenti figure (parabola con asse verticale), è importante osservare che la tangente alla parabola nel suo vertice passa per il punto medio {M} del segmento {\overline{FH}}. Inoltre, il punto medio {M} è anche il punto di intersezione tra la retta tangente {t} e la perpendicolare a {t} condotta per {F}.
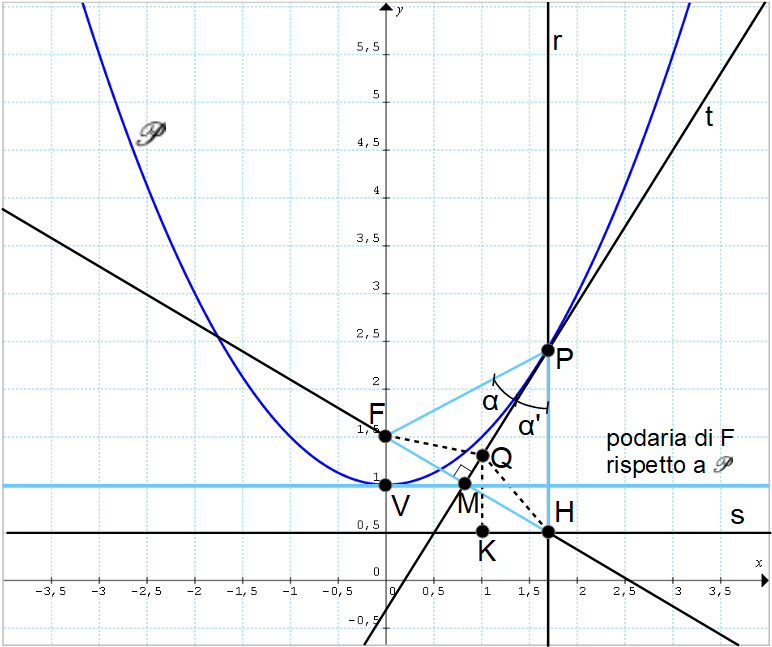
Ora, il punto {M} è detto piede della perpendicolare a {t} condotta dal punto {F} fino a {t}. Ed in particolare, per ogni punto {P} della parabola (diverso dal vertice), la perpendicolare alla corrispondente retta tangente {t} condotta da {F} a {t} avrà come piede un punto {M} comunque appartenente alla tangente alla parabola nel suo vertice.
Così, per una parabola con asse orizzontale o verticale (o in generale anche obliquo) vale il seguente enunciato.
La retta tangente ad una parabola {\mathscr{P}} nel suo vertice è il luogo dei piedi delle perpendicolari condotte dal fuoco {F} alle tangenti {t} alla parabola {\mathscr{P}} e si chiama podaria di {F} rispetto a {\mathscr{P}}.
Proprietà del fuoco della parabola
Ora che sappiamo che la bisettrice interna dell’angolo {\stackrel{\angle}{PFH}} coincide con la tangente alla parabola {\mathscr{P}} nel punto {P} possiamo introdurre un’importante proprietà ottica del fuoco di una parabola (consideriamo per ora il caso di una parabola con asse verticale).
In generale, data una superficie riflettente piana, un raggio di luce che incide sulla superficie viene riflesso lungo una direzione che dipende dalla direzione di arrivo del raggio di luce. In particolare, se il raggio di luce incide su di una superficie riflettente piana perpendicolarmente ad essa, questo viene riflesso di nuovo lungo la direzione perpendicolare. Diversamente, se il raggio incide su detta superficie formando però con la perpendicolare {n} alla superficie stessa un angolo di incidenza {\hat{i}}, questo verrà riflesso lungo una direzione corrispondente all’angolo di riflessione {\hat{r}}, come nella figura a seguire:
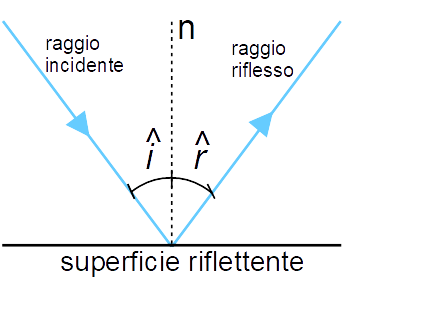
Come è immediato osservare dalla figura, i due angoli (geometrici) condividono la stessa ampiezza, ovvero si ha {\hat{i}=\hat{r}}.
Ora, se la superficie riflettente non è piana, la legge di riflessione appena mostrata continua comunque a valere. Consideriamo in particolare come superficie riflettente la superficie interna di un paraboloide di rivoluzione.
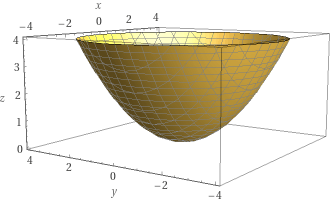
Tale superficie vista in sezione è data da una parabola ad esempio con asse verticale:
Nota: un paraboloide di rivoluzione è una superficie dello spazio che si ottiene facendo ruotare una parabola attorno al proprio asse.
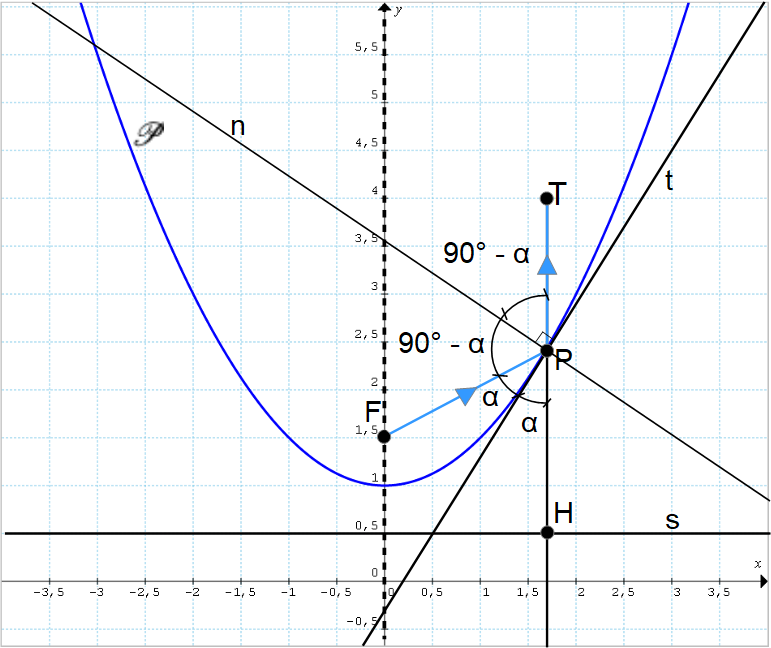
Supponiamo che dal fuoco della parabola venga emesso un raggio {FP}. Tale raggio incide sulla superficie della parabola (vista in sezione) nel punto {P}. Ora, per applicare la legge di riflessione, cerchiamo di ricondurci al caso piano.
Per fare questo, consideriamo la retta {t} tangente alla parabola nel punto {P}. Sempre in sezione, possiamo vedere tale retta come la superficie riflettente. Ciò ha senso considerando un raggio che incide nel punto {P}, poiché tale punto è in comune con la retta {t} e con la parabola {\mathscr{P}}. Per cui possiamo applicare la legge di riflessione vista nel caso di una superficie piana, e di conseguenza l’angolo che il raggio {FP} forma con la perpendicolare a {t} è lo stesso dell’angolo che il raggio riflesso {PT} forma con la stessa perpendicolare (gli angoli sono intesi come in figura).
Ora, per la proprietà della tangente alla parabola in un dato punto {P}, sappiamo che la retta tangente {t} è la bisettrice dell’angolo {\stackrel{\angle}{PFH}}. Di conseguenza, con riferimento alla figura, l’angolo di incidenza relativo al raggio {FP} dovrà essere necessariamente uguale a {90°-\alpha}. Ma per la legge di riflessione, l’angolo di riflessione relativo al raggio {PT} dovrà anch’esso essere uguale a {90°-\alpha}. Da ciò discende che il raggio {PT} è diretto lunga la direzione parallela all’asse della parabola.
Infatti, l’angolo {\stackrel{\angle}{PHT}} è uguale a {\alpha+\alpha+90°-\alpha+90°-\alpha=180°}. Inoltre, sempre per la proprietà della tangente alla parabola in un dato punto, il punto {H} è necessariamente il piede della perpendicolare condotta da {P} alla direttrice {s} della parabola. Di conseguenza, il raggio {PT} ha direzione verticale, come l’asse della parabola.
Si può inoltre dimostrare che vale anche il viceversa: se un raggio incide sulla superficie interna di una parabola con asse verticale (sempre vista in sezione) in direzione verticale, questo verrà riflesso sul fuoco della parabola.
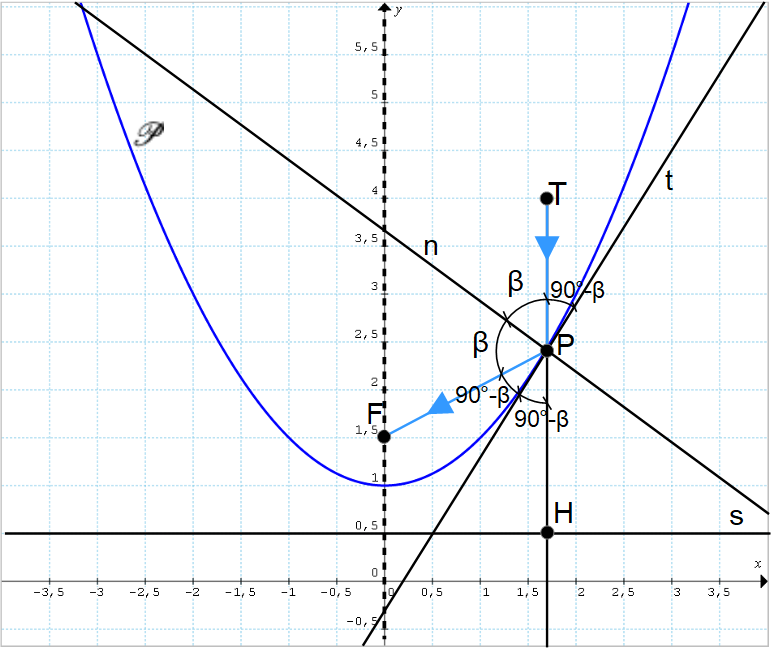
Infatti, supponiamo che il raggio {TP} incida sulla superficie interna della parabola {\mathscr{P}} (vista in sezione) nel punto {P} e con direzione parallela all’asse della parabola stessa. Indichiamo con {\beta} l’angolo di incidenza del raggio {TP} relativamente alla normale alla superficie piana rappresentata in sezione della retta tangente {t}. Per la legge di riflessione, anche l’angolo di riflessione relativo al raggio {PF} sarà ancora {\beta}.
Ora, poiché {n} è perpendicolare a {t}, l’angolo con vertice in {P} e compreso fra il raggio {PF} e la retta {t} sarà uguale a {90° - \beta}. Inoltre, per lo stesso motivo anche l’angolo con vertice in {P} e compreso fra il raggio {TP} e la retta tangente {t} sarà uguale a {90° - \beta}.
A questo punto è fondamentale osservare che l’angolo sempre con vertice in {P} e avente per lati la retta tangente {t} e la retta passante per i punti {P} e {H} è opposto all’angolo compreso fra {t} e il raggio {TP}. Quindi tale angolo avrà ampiezza uguale a {90° - \beta}. Di conseguenza, gli angoli compresi fra {t} e rispettivamente il raggio {PF} e la retta passante per {P} e {H} sono tra loro uguali.
Pertanto, la retta {t} è la bisettrice dell’angolo {\stackrel{\angle}{PFH}} e quindi il punto {F}, ovvero il punto nel quale viene riflesso il raggio {TP}, con {P} punto appartenente alla parabola, non potrà essere che il fuoco della parabola stessa (vedi la proprietà esposta all’inizio della lezione).
Abbiamo quindi dimostrato, per una parabola con asse verticale, che se un raggio di luce viene emesso dal fuoco della parabola verso un punto interno alla parabola stessa, tale raggio viene riflesso lungo la direzione verticale. Viceversa, se un raggio di luce incide su di un punto della superficie interna della parabola ed ha direzione verticale, questo viene riflesso sul fuoco della parabola.
Infine, le considerazioni fatte possono essere estese anche al caso di una parabola con asse orizzontale o comunque con asse obliquo. Così, in conclusione, vale per una parabola la seguente proprietà ottica del fuoco, che possiamo esprimere nei due seguenti modi:
- se un raggio di luce viene emesso dal fuoco della parabola, questo viene riflesso su un dato punto {P} della superficie della parabola in direzione parallela all’asse della parabola stessa;
- se viceversa un raggio di luce incide su un certo punto {P} della superficie interna di una parabola in direzione parallela all’asse della parabola, questo viene riflesso sul fuoco della parabola.
Conclusioni
Per quanto riguarda questa lezione sulla proprietà ottica del fuoco di una parabola è tutto. Abbiamo così visto un risultato che ha importanti applicazioni pratiche, sia nel campo dell’ottica, sia nel campo della trasmissione e ricezione di onde elettromagnetiche. Infatti, a partire dalle proprietà sin qui esposte della parabola, un apparecchio a forma di paraboloide di rivoluzione può essere convenientemente utilizzato per tali scopi.
Nella prossima lezione ci occuperemo del teorema di Archimede. Un saluto a tutti voi e, come sempre, buono studio con SìMatematica!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
