Esercizi sulle condizioni per individuare una circonferenza

 - 

Esercizi sulla circonferenza (scuole superiori)

Gli esercizi sulle condizioni per individuare una circonferenza che presentiamo in questa scheda si basano sulle quattro casistiche viste nella lezione teorica:

• come determinare l’equazione di una circonferenza a partire dalle coordinate di tre punti del piano non allineati;
• come determinare l’equazione di una circonferenza a partire dalle coordinate del centro e di un punto appartenente alla circonferenza stessa;
• ancora, come scrivere l’equazione di una circonferenza a partire dalle coordinate di due suoi punti e dall’equazione di una retta passante per il centro della circonferenza stessa;
• infine, come individuare una circonferenza a partire dalle coordinate del suo centro e dall’equazione di una retta tangente alla circonferenza stessa.

Nello svolgere gli esercizi sulle condizioni per individuare una circonferenza nel piano è importante ricordare che è possibile scrivere l’equazione di una circonferenza una volta note le coordinate del suo centro e la misura del suo raggio. In particolare, è possibile scrivere l’equazione della circonferenza di centro {C=(x_C, y_C)} e raggio {r} nella forma con centro e raggio noti:

(x-x_C)^2+(y-y_C)^2=r^2

Utilizzando le opportune formule o comunque calcolando i quadrati e riordinando i termini è possibile infine ricondurre l’equazione alla forma canonica:

x^2+y^2+ax+by+c=0

Per maggiori dettagli in merito è disponibile la lezione sull’equazione della circonferenza. Proseguiamo ora riassumendo brevemente i quattro casi delle condizioni per individuare una circonferenza nel piano.

Supponiamo di conoscere tre punti {P_1=(x_1,y_1), P_2=(x_2,y_2), P_3=(x_3,y_3)} per i quali passa una certa circonferenza. Per determinare l’equazione in forma canonica di tale circonferenza, necessitiamo dei coefficienti {a,b,c}. Ma questi si possono in questo caso ricavare risolvendo rispetto alle incognite {a,b,c} il seguente sistema:

\begin{cases} x_1^2+y_1^2+ax_1+by_1+c=0 \\ \\ x_2^2+y_2^2+ax_2+by_2+c=0\\ \\ x_3^2+y_3^2+ax_3+by_3+c=0\end{cases}

In alternativa, è possibile ricercare il centro della circonferenza come intersezione fra gli assi dei segmenti {\overline{P_1P_2}} e {\overline{P_2P_3}}, e quindi calcolare il raggio come distanza fra il centro e uno fra i punti {P_1, P_2, P_3}. In tal modo, sarà possibile scrivere l’equazione della circonferenza nella forma con centro e raggio, e quindi eventualmente riesprimere l’equazione nella forma canonica.

Passando ad un altro caso, se sono invece note le coordinate del centro della circonferenza e di un suo punto, è immediato calcolare la misura del raggio come distanza fra il centro {C=(x_C, y_C)} e il punto {P=(x_P, y_P)} dato:

r=\sqrt{(x_p-x_C)^2+(y_P-y_C)^2}

Una volta noto il raggio, sarà possibile scrivere l’equazione della circonferenza poiché sono anche note le coordinate del centro.

Negli esercizi sulle condizioni per individuare una circonferenza sarà anche possibile trovarsi nel caso in cui vengano fornite le coordinate di due punti della circonferenza e l’equazione di una retta passante per il centro della circonferenza stessa. In tal caso, potremo calcolare le coordinate del centro della circonferenza come intersezione fra la retta della quale è data l’equazione e l’asse del segmento che unisce i due punti dati. A tal punto, una volta calcolato anche il raggio sarà possibile scrivere l’equazione della circonferenza.

Occupandoci infine dell’ultimo caso per questo tipo di esercizi, come condizioni per individuare l’equazione di una circonferenza ci possono venire fornite le coordinate del centro della circonferenza e l’equazione di una retta tangente alla circonferenza stessa. In tal caso, basterà calcolare il raggio come la distanza fra la retta tangente e il centro della circonferenza. A tal punto, noti centro e raggio sarà possibile scrivere l’equazione della circonferenza.

Importante. Per comprendere appieno i seguenti esercizi è fondamentale aver ben presente la lezione teorica sulle condizioni per individuare una circonferenza.

Esercizi sulle condizioni per individuare una circonferenza, svolti e commentati

Esercizio 1

Scrivere l’equazione della circonferenza che ha per diametro il segmento {\overline{AB}} con {A=(1,0)} e {B=(3,2)}.

Cominciamo calcolando il punto medio del segmento. Questo sarà il centro {C} della circonferenza, in quanto i punti {A} e {B} sono gli estremi di un diametro della circonferenza.

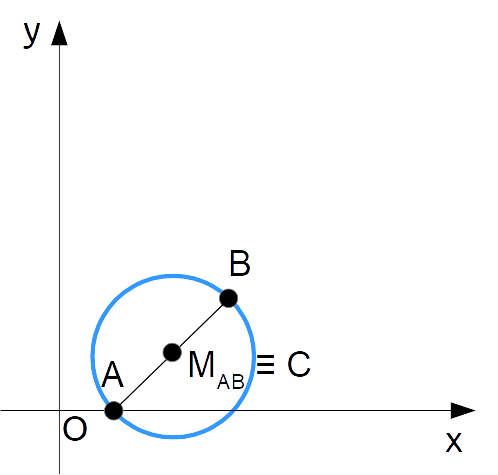
Si ha:

M_{AB}=\left( \dfrac{x_A+x_B}{2}, \dfrac{y_A+y_B}{2}\right)=\left( \dfrac{1+3}{2}, \dfrac{0+2}{2}\right)=(2,1)=C

Calcoliamo ora il raggio come distanza fra il centro {C} e uno dei due punti {A} e {B}. Considerando ad esempio la distanza fra {C} e {A} otteniamo:

r=\sqrt{(x_C-x_A)^2+(y_C-y_A)^2}=\sqrt{(2-1)^2+(1-0)^2}=\sqrt{2}

Così in conclusione la circonferenza ha equazione, nella forma con centro e raggio noti:

(x-2)^2+(y-1)^2=2

Esercizio 2

Scrivere l’equazione della circonferenza avente centro {C=(1,3)} e tangente alla retta {t:4x-5y+1=0}.

La misura del raggio {r} della circonferenza è data dalla distanza fra la retta {t} e il centro {C} della circonferenza (vedi: distanza di un punto da una retta).

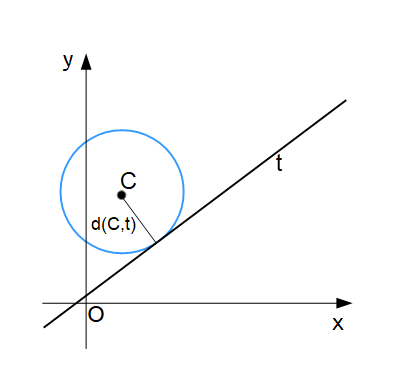
Indicati con {a_1,b_1,c_1} i coefficienti nell’equazione della retta {t} e con {x_C} e {y_C} le coordinate del centro {C} abbiamo:

d(C,t)=\dfrac{|a_1x_C+b_1y_C+c_1|}{\sqrt{a_1^2+b_1^2}}=\dfrac{|4 \cdot 1 -5 \cdot 3 +1|}{\sqrt{4^2+(-5)^2}}=\dfrac{10}{\sqrt{41}}

Osserviamo che non serve razionalizzare la misura del raggio ottenuta. Infatti, nello scrivere l’equazione tale valore andrà elevato al quadrato, il che fa comunque sparire la radice al denominatore.

Noti ormai il centro e il raggio della circonferenza possiamo scriverne l’equazione:

(x-1)^2+(y-3)^2=\left( \dfrac{10}{\sqrt{41}}\right)^2

e quindi in conclusione:

(x-1)^2+(y-3)^2=\dfrac{100}{41}

Esercizio 3

Scrivere l’equazione della circonferenza passante per i punti {P_1=(2,5)}, {P_2=(3,7)} e con centro appartenente alla retta di equazione {r_1: 5x+9y-12=0}.

Determiniamo l’equazione dell’asse ad esempio del segmento {\overline{P_1P_2}}. Cominciamo calcolando il punto medio del segmento stesso:

\begin{align*} &M_{12}=\left( \dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)=\left( \dfrac{2+3}{2}, \dfrac{5+7}{2}\right)=\left( \dfrac{5}{2},6\right)\end{align*}

Il coefficiente angolare della retta passante per i punti {P_1} e {P_2} è:

m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{7-5}{3-2}=2

Ora, per scrivere l’equazione dell’asse del segmento, utilizziamo la formula della retta passante per un punto con pendenza nota e la relazione di perpendicolarità fra rette (vedi: retta nel piano). Infatti, l’asse del segmento {\overline{P_1P_2}} è una retta tale da essere perpendicolare al segmento ( e quindi perpendicolare alla retta che passa per {P_1} e {P_2}) e tale inoltre da essere passante per il suo punto medio. Abbiamo quindi:

y-y_{M_{12}}=-\dfrac{1}{m} (x-x_{M_{12}}) 

ovvero, sostituendo i valori:

\begin{align*} &y-6 = -\dfrac{1}{2} \left(x-\dfrac{5}{2}\right); \\ \\ & y=-\dfrac{1}{2}x+\dfrac{5}{4}+6;\\ \\ & y=-\dfrac{1}{2}x+\dfrac{29}{4}\end{align*}

Ora, il centro della circonferenza cercata sarà dato dall’intersezione fra l’asse del segmento {\overline{P_1P_2}} e la retta passante per il centro della circonferenza, ovvero la retta {r_1}. Impostiamo quindi il corrispondente sistema:

\begin{cases} y=-\dfrac{1}{2}x+\dfrac{29}{4} \\ \\ 5x+9y-12=0 \end{cases}

Riscriviamo la seconda equazione a sistema in forma esplicita:

\begin{cases} y=-\dfrac{1}{2}x+\dfrac{29}{4}\\ \\ y=-\dfrac{5}{9}x+\dfrac{4}{3}\end{cases}

Risolvendo il sistema per confronto abbiamo:

\small\begin{cases} -\dfrac{1}{2}x+\dfrac{29}{4}=-\dfrac{5}{9}x+\dfrac{4}{3} \quad \rightarrow \quad \dfrac{1}{18}x= -\dfrac{71}{12} \quad \rightarrow x=-\dfrac{71}{12} \cdot 18=-71 \cdot\dfrac{3}{2}=-\dfrac{213}{2}\\ \\ y=-\dfrac{5}{9}x+\dfrac{4}{3} 
 \quad \rightarrow y=-\dfrac{5}{9} \cdot \left( -\dfrac{213}{2}\right)+\dfrac{4}{3}=\dfrac{5}{3} \cdot \dfrac{71}{2}+\dfrac{8}{6}=\dfrac{355+8}{6}=\dfrac{363}{6}=\dfrac{121}{2}\end{cases} 

Di conseguenza il centro della circonferenza è:

C=\left( -\dfrac{213}{2}, \dfrac{121}{2}\right)

Infine calcoliamo il raggio della circonferenza come distanza fra il centro e ad esempio il punto {P_1}:

\begin{align*} & r=\overline{CP_1}=\sqrt{(x_{P_{1}}-x_{C})^2+(y_{P_{1}}-y_C)^2}=\\ \\ & =\sqrt{\left( 2+\dfrac{213}{2}\right)^2+\left( 5-\dfrac{121}{2}\right)^2} = \sqrt{\left( \dfrac{217}{2}\right)^2+\left(-\dfrac{111}{2}\right)^2} = \\ \\ & =\sqrt{\dfrac{47089}{4}+\dfrac{12321}{4}}=\sqrt{\dfrac{29705}{2}}\end{align*}

Così in conclusione la circonferenza cercata ha equazione:

\left( x+\dfrac{213}{2}\right)^2+\left( y-\dfrac{121}{2}\right)^2=\dfrac{29705}{2}

Esercizio 4

Scrivere l’equazione della circonferenza passante per il punto {(P=6,4)} e avente centro {C=(3,0)}.

Calcoliamo il raggio della circonferenza come distanza tra il punto {P} appartenente alla circonferenza e il centro {C} della stessa:

\small r=\sqrt{(x_P-x_C)^2+(y_P-y_C)^2}=\sqrt{(6-3)^2+(4-0)^2}=\sqrt{9+16}=\sqrt{25}=5

A questo punto è immediato scrivere l’equazione della circonferenza, in quanto centro e raggio sono ormai entrambi noti:

(x-x_C)^2+(y-y_C)^2=r^2 \quad \Rightarrow  \quad (x-3)^2+(y-0)^2=5^2

ovvero in forma canonica:

\begin{align*} &x^2-6x+9+y^2-25=0; \\ \\ & \boxed{x^2+y^2-6x-16=0}\end{align*}

Esercizio 5

Scrivere l’equazione della circonferenza passante per i punti non allineati {P_1=(0,0), P_2=(1,2), P_3=(-2,1)}.

Per questo esercizio utilizziamo il metodo della ricerca del centro e del raggio.

Cominciamo ricercando le coordinate del centro. A tale scopo, consideriamo prima di tutto due segmenti aventi ciascuno per estremi due fra i punti dati. Ad esempio, scegliamo di lavorare con i segmenti {\overline{P_1P_2}} e {\overline{P_2P_3}}.

Calcoliamo i punti medi dei segmenti:

\begin{align*} &M_{12}=\left( \dfrac{0+1}{2}, \dfrac{0+2}{2}\right)=\left( \dfrac{1}{2}, 1\right);\\ \\ & M_{23}=\left( \dfrac{1-2}{2}, \dfrac{2+1}{2}\right)=\left( -\dfrac{1}{2}, \dfrac{3}{2}\right)\end{align*}

Proseguiamo calcolando i coefficienti angolari delle rette passanti rispettivamente per {P_1, P_2} e per {P_2, P_3}:

\begin{align*} &m_{12}=\dfrac{y_{P_{2}}-y_{P_1}}{x_{P_{2}}-x_{P_1}}=\dfrac{2-0}{1-0}=2;\\ \\ & m_{23}=\dfrac{y_{P_3}-y_{P_2}}{x_{P_3}-x_{P_2}}=\dfrac{1-2}{-2-1}=\dfrac{-1}{-3}=\dfrac{1}{3}\end{align*}

Ora disponiamo di tutti i dati per poter scrivere le equazioni degli assi dei segmenti {\overline{P_1P_2}} e {\overline{P_2P_3}}:

\small \begin{align*} &y-y_{M_{12}}=-\dfrac{1}{m_{12}} \cdot (x-x_{M_{12}} )\quad \Rightarrow \quad y-1=-\dfrac{1}{2} \left( x-\dfrac{1}{2}\right) \quad \Rightarrow \quad y=-\dfrac{1}{2}x+\dfrac{5}{4}; \\ \\ & y-y_{M_{23}}=-\dfrac{1}{m_{23} } \cdot(x-x_{M_{23}}) \quad \Rightarrow \quad y-\dfrac{3}{2}=-\dfrac{1}{\frac{1}{3}} \left( x+\dfrac{1}{2}\right) \quad \Rightarrow \quad y=-3x \quad\end{align*}

Il centro della circonferenza è dato dall’intersezione tra gli assi dei due segmenti:

\begin{cases} y=-\dfrac{1}{2}x+\dfrac{5}{4} \\ \\ y=-3x\end{cases}

Risolvendo il sistema con il metodo del confronto:

\begin{cases} -\dfrac{1}{2}x+\dfrac{5}{4}=-3x \quad \rightarrow \quad x=-\dfrac{5}{4} \cdot \dfrac{2}{5}=-\dfrac{1}{2} \\ \\ y=-3x \quad \rightarrow \quad y=-3 \cdot \left( -\dfrac{1}{2}\right)=\dfrac{3}{2}\end{cases}

Di conseguenza il centro della circonferenza è {C=\left( -\dfrac{1}{2}, \dfrac{3}{2}\right)}, e in questo particolare caso coincide con il punto medio del segmento {\overline{P_2P_3}}.

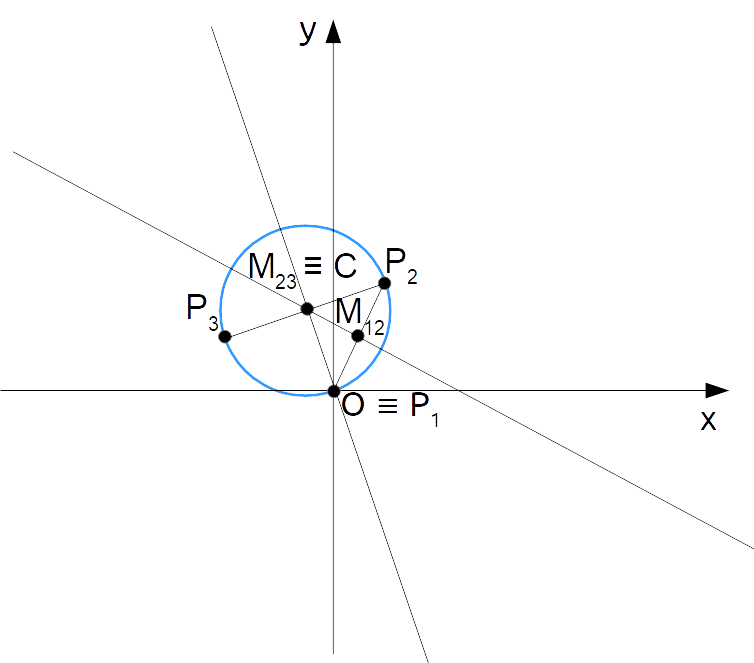
A questo punto calcoliamo il raggio della circonferenza come distanza ad esempio tra il punto {P_1} e il centro {C}:

\begin{align*} & r=\sqrt{(x_C-x_{P_1})^2+(y_C-y_{P_1})^2}=\sqrt{\left( -\dfrac{1}{2}-0\right)^2+\left( \dfrac{3}{2}-0\right)^2}=\\ \\ & =\sqrt{\dfrac{1}{4}+\dfrac{9}{4}}=\sqrt{\dfrac{10}{4}} =\sqrt{\dfrac{5}{2}}\end{align*}

Ora è possibile scrivere l’equazione della circonferenza:

(x-x_C)^2+(y-y_C)^2=r^2 \quad \Rightarrow \quad \left( x+\dfrac{1}{2}\right)^2+\left( y-\dfrac{3}{2}\right)^2=\dfrac{5}{2}

ovvero in forma canonica:

\begin{align*} &x^2+x+\dfrac{1}{4}+y^2-3y+\dfrac{9}{4}-\dfrac{5}{2}=0; \\ \\ &\boxed{ x^2+y^2+x-3y=0}\end{align*}

Dopo aver concluso questo svolgimento, proseguiamo questa serie di esercizi sulle condizioni per individuare una circonferenza con il seguente.

Esercizio 6

Scrivere l’equazione della circonferenza passante per i punti non allineati {P_1=(1,2), P_2=(3,0)} e {P_3=(0, \sqrt{3})}.

Invece del metodo utilizzato nell’esercizio precedente, scegliamo per questo esercizio il metodo basato sulle condizioni di appartenenza dei punti alla circonferenza.

Si tratta di mettere a sistema le condizioni di appartenenza di ciascuno dei punti dati alla circonferenza:

\begin{cases} x_1^2+y_1^2+ax_1+by_1+c=0 \\ \\ x_2^2+y_2^2+ax_2+by_2+c=0 \\ \\ x_3^2+y_3^2+ax_3+by_3+c=0\end{cases}

In pratica ciascuna equazione impone che il rispettivo punto soddisfi l’equazione della circonferenza avente equazione canonica con coefficienti incogniti {a,b,c}. Così dobbiamo sostituire nel sistema le coordinate dei punti {P_1, P_2, P_3} e risolvere il sistema stesso nelle incognite {a,b,c}. Sostituendo i valori noti abbiamo:

\begin{cases} 1^2+2^2+a+2b+c=0 \\ \\ 3^2+0^2+3a+0b+c=0 \\ \\ 0^2+(\sqrt{3})^2+0a+\sqrt{3}b+c=0\end{cases}

Riscrivendo il sistema in forma normale:

\begin{cases} a+2b+c=-5 \\ \\ 3a+c=-9 \\ \\ \sqrt{3}b+c=-3\end{cases}

Proviamo a risolvere il sistema per riduzione. Sostituiamo alla prima equazione a sistema l’equazione che si ottiene sottraendo membro a membro alla prima equazione la seconda:

\begin{cases} -2a+2b=4 \\ \\ 3a+c=-9 \\ \\ \sqrt{3}b+c=-3\end{cases}

Adesso sostituiamo alla seconda equazione a sistema l’equazione che si ottiene sottraendo membro a membro alla seconda equazione la terza:

\begin{cases} -2a+2b=4 \\ \\ 3a-\sqrt{3}b=-6 \\ \\ \sqrt{3}b+c=-3\end{cases}

Ora consideriamo per il momento soltanto le prime due equazioni. Risolviamo il sistema di due equazioni in due incognite corrispondente ad esempio per sostituzione:

\begin{cases} b=\dfrac{4+2a}{2} \\ \\ 3a-\sqrt{3}\left( \dfrac{4+2a}{2}\right)=-6 \quad \rightarrow \quad 
 a = -2 \\ \\ \dots\end{cases}

Di conseguenza per {b} otteniamo:

\begin{cases} b=\dfrac{4+2a}{2} \quad \rightarrow \quad 0 \\ \\
 a = -2 \\ \\ \dots\end{cases}

Infine riprendendo la terza equazione possiamo calcolare il valore del coefficiente {c}:

\begin{cases} b=0 \\ \\
 a = -2 \\ \\ c=-3-\sqrt{3}b=-3\end{cases}

Quindi i coefficienti dell’equazione in forma canonica della circonferenza che stiamo cercando sono {a=-2, b=0, c=-3}. Di conseguenza l’equazione della circonferenza è:

x^2+y^2-2x-3=0

Concludiamo questa serie di esercizi sulle condizioni per individuare una circonferenza con il seguente.

Esercizio 7

Scrivere l’equazione della circonferenza passante per il punto {P=(4,2)} e tangente alla retta {y=x} nel punto {T=(1,1)}.

L’esercizio è leggermente differente rispetto a quelli sin qui visti ed effettivamente rappresenta almeno apparentemente un caso a sé rispetto alle condizioni per individuare una circonferenza esposte nella lezione teorica. Tuttavia, come mostreremo fra un istante i ragionamenti da fare sono del tutti simili rispetto a quelli sinora utilizzati.

Rappresentiamo graficamente la situazione:

Per scrivere l’equazione della circonferenza abbiamo chiaramente bisogno delle coordinate del centro {C}. Ora, è anzitutto importante osservare che la distanza tra il punto di tangenza e il centro della circonferenza è uguale al raggio. Ciò è evidente poiché il punto {T} appartiene alla circonferenza. Riflettendo su ciò, non è troppo difficile convincersi che la la perpendicolare alla retta tangente {y=x} passante per {T} è passante per il centro. Inoltre, l’asse del segmento {\overline{TP}} sarà anch’esso passante per il centro, poiché è l’asse di un segmento avente per estremi due punti appartenenti alla circonferenza.

Di conseguenza, possiamo ottenere il centro della circonferenza come intersezione della retta {r_1} perpendicolare a {y=x} e passante per {T} e l’asse {r_2} del segmento {\overline{TP}}:

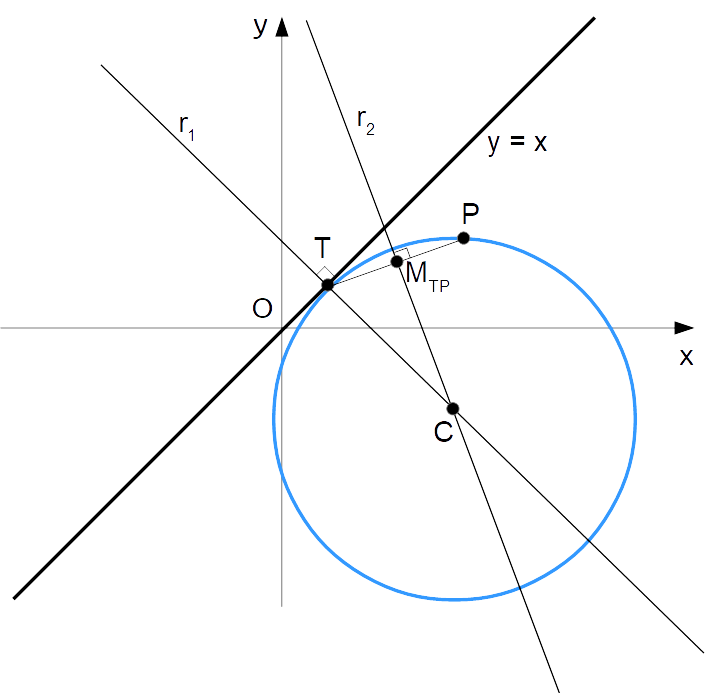
Ora non ci resta che tradurre tale rappresentazione grafica nel linguaggio della geometria analitica.

Cominciamo scrivendo l’equazione della retta perpendicolare ad {y=x} e passante per il punto {T=(1,1)}. Osservando che per la retta {y=x} abbiamo coefficiente angolare {m=1}, possiamo scrivere:

y-1=-1(x-1) \quad \Rightarrow \quad r_1: y=-x+2

Ora scriviamo l’equazione di {r_2}, ovvero l’asse del segmento {\overline{TP}}. Per fare questo, calcoliamo le coordinate del punto medio di tale segmento ed inoltre il coefficiente angolare della retta passante per {T} e {P}:

\begin{align*} & M_{TP}=\left( \dfrac{4+1}{2}, \dfrac{2+1}{2}\right)=\left( \dfrac{5}{2}, \dfrac{3}{2}\right) ;\\ \\ & m_{TP}=\dfrac{y_P-y_T}{x_P-x_T}=\dfrac{2-1}{4-1}=\dfrac{1}{3}\end{align*}

Così per l’equazione di {r_2} abbiamo:

y-y_{M_{TP}}=-\dfrac{1}{m_{TP}}(x-x_{M_{TP}})

ovvero sostituendo i valori e sviluppando i calcoli:

\begin{align*} &y-\dfrac{3}{2}=-3\left( x-\dfrac{5}{2}\right);\\ \\ &y=-3x+\dfrac{15}{2}+\dfrac{3}{2};\\ \\ &r_2: y=-3x+9\end{align*}

A questo punto possiamo ricavare le coordinate del centro come intersezione tra le due rette {r_1} ed {r_2}:

\begin{cases}  r_1: y=-x+2 \\ \\ r_2: y=-3x+9\end{cases}

Risolvendo il sistema per confronto otteniamo:

\begin{cases} -x+2=-3x+9 \quad \rightarrow \quad x=\dfrac{7}{2} \\ \\ y=-3 \cdot \dfrac{7}{2}+9  \quad \rightarrow \quad  y=-\dfrac{3}{2}\end{cases}

Così il centro della circonferenza è {C=\left( \dfrac{7}{2}, -\dfrac{3}{2}\right)}. Infine per il raggio della circonferenza abbiamo ad esempio:

\begin{align*} & r=\sqrt{(x_C-x_P)^2+(y_C-y_P)^2}=\sqrt{\left( \dfrac{7}{2}-4\right)^2+\left( -\dfrac{3}{2}-2\right)^2}= \\ \\ & =\sqrt{\dfrac{1}{4}+\dfrac{49}{4}}=\sqrt{\dfrac{50}{4}}=\sqrt{\dfrac{25}{2}}\end{align*}

Così noti centro e raggio, per l’equazione della circonferenza cercata abbiamo in conclusione:

\left( x-\dfrac{7}{2}\right)^2+\left(y+\dfrac{3}{2}\right)^2=\dfrac{25}{2}

L’esercizio appena risolto è a ben vedere un parente stretto dell’esercizio 5. Quindi siamo in un caso molto simile a quello del problema della circonferenza per tre punti risolto con il metodo della ricerca del centro e del raggio. In questo caso, tuttavia, ci vengono dati due soli punti della circonferenza, ma abbiamo comunque l’equazione della retta tangente alla circonferenza in uno dei due punti. Così, una retta passante per il centro è già praticamente nota ed è in particolare la retta perpendicolare alla retta tangente e passante per il punto di tangenza. Infine, come nel caso dell’esercizio 5, un’altra retta passante per il centro si ottiene scrivendo l’equazione dell’asse del segmento avente per estremi i due punti noti della circonferenza. A tal punto le coordinate del centro della circonferenza si ottengono come intersezione delle due rette passanti per il centro. Infine, la determinazione della misura del raggio è banale (distanza fra il centro della circonferenza e un qualsiasi punto della circonferenza stessa).

Come ragionamento alternativo, possiamo anche vedere l’esercizio appena svolto come uno stretto parente dell’esercizio 3. Infatti, anche se non ci viene data l’equazione di una retta passante per il centro, ci viene dato comunque modo di scriverla con non troppa difficoltà a partire dall’equazione della retta tangente alla circonferenza e dalle coordinate del punto di tangenza. Per il resto le considerazioni da fare sono del tutto simili a quelle sin qui viste.

Conclusioni

Per quanto riguarda questa serie di esercizi sulle condizioni per individuare una circonferenza è tutto. In caso di dubbi vi rimandiamo alla lezione teorica correlata, che è disponibile nel link a seguire.

Un saluto a tutti voi e come sempre, buono studio con SìMatematica!