Esercizi sulla tangente ad una circonferenza in un punto

 - 

Esercizi sulla circonferenza (scuole superiori)

In questa scheda proponiamo degli esercizi svolti sulla tangente ad una circonferenza in un punto. In tutti gli esercizi avremo a che fare con il caso di retta tangente in un punto appartenente alla circonferenza. Il caso relativo alle rette tangenti ad una circonferenza in un punto esterno alla circonferenza stessa viene invece trattato nella relativa lezione.

I metodi che qui utilizzeremo per lo svolgimento degli esercizi sulla retta tangente ad una circonferenza in un punto sono due:

• metodo basato sulla relazione di perpendicolarità fra rette (rette perpendicolari);
• utilizzo delle formule di sdoppiamento della circonferenza.

Abbiamo già trattato i metodi nella lezione sulla determinazione dell’equazione della retta tangente ad una circonferenza in un suo punto, tuttavia nella presente scheda forniremo comunque i richiami teorici necessari.

Negli esercizi sulla tangente ad una circonferenza in un punto presenti in questa scheda, per il loro svolgimento utilizzeremo in alternativa uno dei due metodi, ma a volte forniremo lo svolgimento con entrambi i metodi, in modo da poter effettuare un confronto.

Prima di iniziare gli esercizi forniamo dei brevi richiami.

Il metodo che utilizza la perpendicolarità tra rette si basa sul fatto che la retta {t} tangente ad una circonferenza in un punto {P} della circonferenza stessa è perpendicolare alla retta {r_{CP}} passante per il centro della circonferenza e per il punto {P} stesso.

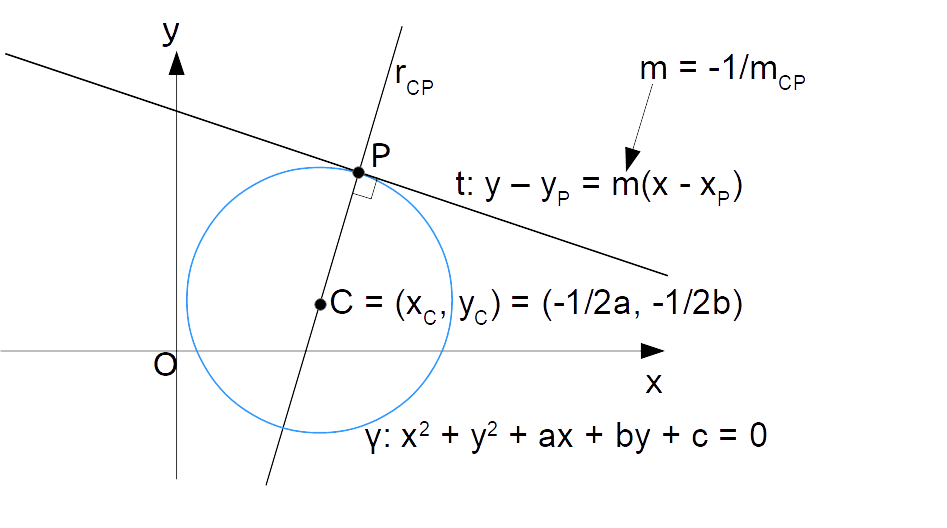
L’idea è quella di ricavare il coefficiente angolare {m_{CP}} a partire dalle coordinate dei punti {C} e {P}, per poi calcolare il coefficiente angolare della retta tangente {t} mediante la relazione:

m=-\dfrac{1}{m_{CP}}

che esprime la perpendicolarità fra la retta {t} e la retta {r_{CP}}.

A tal punto sfruttando la formula della retta passante per un punto con coefficiente angolare noto si può scrivere l’equazione della retta tangente alla circonferenza nel punto {P} come:

t: y-y_P=m(x-x_P)

Il metodo presenta l’inconveniente di poter essere applicabile esattamente secondo la procedura appena descritta soltanto nel caso di rette tangenti non parallele agli assi coordinati (ovvero né orizzontali, né verticali). Tuttavia, con semplici accorgimenti è possibile estendere il metodo anche a questi casi.

Le formule di sdoppiamento per la circonferenza non richiedono invece particolari ragionamenti. A partire dall’equazione della circonferenza in forma canonica, noto il punto {P=(x_P, y_P)} di tangenza, basta effettuare sull’equazione stessa le seguenti sostituzioni:

x^2 \rightarrow x_P\cdot x, \qquad y^2\rightarrow y_P \cdot y, \qquad x\rightarrow \dfrac{x+x_P}{2}, \qquad y\rightarrow \dfrac{y+y_P}{2}

In tal modo si ricade in un’equazione di primo grado che rappresenta proprio la retta tangente alla circonferenza nel punto {P} ad essa appartenente.

Quest’ultimo metodo è valido senza alcun accorgimento in più anche nel caso di rette tangenti orizzontali o verticali, e probabilmente è quello più indicato per gli esercizi sulla retta tangente ad una circonferenza in un punto. Tuttavia, il primo metodo è una valida alternativa, specialmente se non si ricordano le formule di sdoppiamento.

Esercizi svolti e commentati sulla retta tangente ad una circonferenza in un punto

Esercizio 1

Determinare l’equazione della retta tangente alla circonferenza reale non degenere di equazione {x^2+y^2+4x+2y-8=0} nel suo punto {P=(1,-3)}.

Per questo primo esercizio vediamo l’utilizzo di entrambi i metodi.

Relazione di perpendicolarità fra rette. Cominciamo calcolando le coordinate del centro della circonferenza. Queste si possono calcolare a partire dai coefficienti {a} e {b} presenti nell’equazione in forma canonica della circonferenza, come segue:

x_C=-\dfrac{1}{2}a, \qquad y_C=-\dfrac{1}{2}b

Nel nostro caso, confrontando l’equazione in forma canonica di una generica circonferenza:

x^2+y^2+ax+by+c=0

con l’equazione data nel testo, abbiamo {a=4} e {b=2}. Di conseguenza, per le coordinate del centro {C} della circonferenza si ha:

x_C=-\dfrac{1}{2}a=-\dfrac{1}{2}\cdot4=-2; \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2}\cdot2=-1

Così il centro della circonferenza è {C=(-2,-1)}.

A questo punto, essendo note sia le coordinate del punto {P}, sia le coordinate del punto {C}, possiamo calcolare il coefficiente angolare della retta passante per tali due punti:

m_{CP}=\dfrac{y_P-y_C}{x_P-x_C}=\dfrac{-3-(-1)}{1-(-2)}=\dfrac{-3+1}{1+2}=-\dfrac{2}{3}

Osserviamo che abbiamo potuto calcolare il coefficiente angolare poiché in questo caso si ha {x_P \neq x_C}. Inoltre, otteniamo un valore per il coefficiente angolare non nullo poiché {y_P \neq y_C}.

Ora, poiché la retta {r_{CP}} è perpendicolare alla retta tangente cercata, per quest’ultima il coefficiente angolare è dato da (vedi: rette perpendicolari):

m=-\dfrac{1}{m_{CP}}=-\dfrac{1}{-\frac{2}{3}}=\dfrac{3}{2}

Infine, poiché la retta tangente {t} passa per il punto {P}, ed essendo noto il suo coefficiente angolare, per l’equazione di tale retta possiamo scrivere:

t:y-y_P=m(x-x_P)

ovvero sostituendo i valori:

\begin{align*} &y-(-3)=\dfrac{3}{2} (x-1);\\ \\ & y+3=\dfrac{3}{2}x-\dfrac{3}{2};\\ \\ & \boxed{t:y=\dfrac{3}{2}x-\dfrac{9}{2}}\end{align*}

e questa in conclusione è l’equazione della retta tangente alla circonferenza data nel punto {P=(1,-3)}.

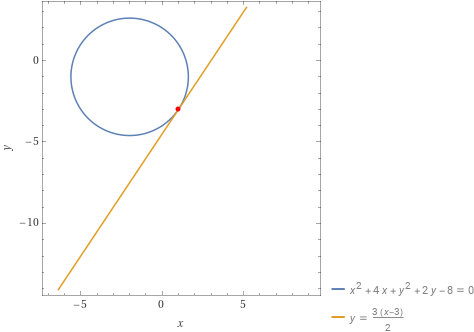
Formula di sdoppiamento. Essendo note le coordinate {x_P} ed {y_P} del punto {P} di tangenza, basta effettuare nell’equazione in forma canonica della circonferenza le sostituzioni:

x^2 \rightarrow x_P\cdot x, \qquad y^2\rightarrow y_P \cdot y, \qquad x\rightarrow \dfrac{x+x_P}{2}, \qquad y\rightarrow \dfrac{y+y_P}{2}

che tenendo conto dei valori delle coordinate del punto {P=(1,-3)} divengono:

x^2\rightarrow x, \qquad y^2\rightarrow-3y, \qquad x \rightarrow\dfrac{x+1}{2}, \qquad y \rightarrow\dfrac{y-3}{2}

In pratica si tratta di prendere l’equazione della circonferenza in forma canonica e sostituire alla quantità {x^2} la quantità {x}, alla quantità {y^2} la quantità {-3y}, alla quantità {x} la quantità {\dfrac{x+1}{2}} ed infine alla quantità {y} la quantità {\dfrac{y-3}{2}}. Così abbiamo:

\underbrace{x}_{x^2}+\underbrace{(-3y)}_{y^2}+4 \underbrace{\left(\dfrac{x+1}{2} \right)}_{x}+2 \underbrace{\left( \dfrac{y-3}{2}\right)}_{y}-8=0

ovvero:

x-3y+2x+2+y-3-8=0

e quindi:

t:3x-2y-9=0

ovvero in forma esplicita:

t:y=\dfrac{3}{2}x-\dfrac{9}{2}

Abbiamo così ritrovato correttamente lo stesso risultato già ottenuto con il metodo precedente.

Esercizio 2

Proseguiamo questa serie di esercizi sulla retta tangente ad una circonferenza in un punto con un esercizio che richiede di lavorare con delle quantità irrazionali (radicali). Con ciò vogliamo mostrare come cavarsela anche quando il testo dell’esercizio non agevola particolarmente i calcoli.

Determinare l’equazione della retta tangente alla circonferenza reale non degenere di equazione {x^2+y^2-3x+5y-9=0} nel punto {P=\left( \dfrac{3-\sqrt{6}}{2}, \dfrac{3}{2}\right)}.

Utilizziamo le formule di sdoppiamento. Le sostituzioni da porre sono:

\small x^2\rightarrow \left( \dfrac{3-\sqrt{6}}{2}\right)x,\qquad y^2\rightarrow \dfrac{3}{2}y, \qquad x\rightarrow \dfrac{x+\frac{3-\sqrt{6}}{2}}{2}, \qquad y \rightarrow\dfrac{y+\frac{3}{2}}{2}

Così a partire dall’equazione della circonferenza otteniamo:

\begin{align*} & \dfrac{3-\sqrt{6}}{2}\cdot x+\dfrac{3}{2}y-3 \cdot\dfrac{x+\frac{3-\sqrt{6}}{2}}{2}+5 \cdot \dfrac{y+\frac{3}{2}}{2}-9=0;\\ \\ &\dfrac{3}{2}x-\dfrac{\sqrt{6}}2{x+\dfrac{3}{2}y-\dfrac{3}{2}x-\dfrac{3}{2}\cdot \dfrac{3-\sqrt{6}}{2}}+\dfrac{5}{2}y+\dfrac{5}{2}\cdot\dfrac{3}{2}-9=0;\\ \\ & \dfrac{3}{2}x-\dfrac{\sqrt{6}}{2}x+\dfrac{3}{2}y-\dfrac{3}{2}x+\dfrac{-9+3\sqrt{6}}{4}+\dfrac{5}{2}y+\dfrac{15}{4}-9=0;\\ \\ & \left( \cancel{\dfrac{3}{2}}-\dfrac{\sqrt{6}}{2}-\cancel{\dfrac{3}{2}}\right)x+\left( \dfrac{3}{2}+\dfrac{5}{2}\right)y-\dfrac{9}{4}+\dfrac{3}{4}\sqrt{6} +\dfrac{15}{4}-9=0;\\ \\ &t:-\dfrac{\sqrt{6}}{2}x+4y -\dfrac{15}{2}+\dfrac{3}{4}\sqrt{6}=0\end{align*}

I calcoli sono un po’ lunghi a causa del fatto che l’ascissa del punto {P} è espressa come una quantità irrazionale. In questi casi il trucco sta nel riscrivere l’equazione di partenza come una somma di monomi, per poi raccogliere rispetto ad {x} e rispetto ad {y}, sommando infine tra loro i termini noti. In tal modo riconduciamo l’equazione della retta tangente alla forma implicita {ax+by+c=0}.

Abbiamo così visto come determinare l’equazione della retta tangente alla circonferenza nel punto {P} anche in questo caso. Volendo possiamo anche riscrivere l’equazione della retta {t} in forma esplicita:

t: y=\dfrac{\sqrt{6}}{8}x+\dfrac{15}{8}-\dfrac{3}{16}\sqrt{6}

ovvero se preferite:

t:y=\dfrac{1}{16}\left( 2\sqrt{6}x+30-3\sqrt{6}\right)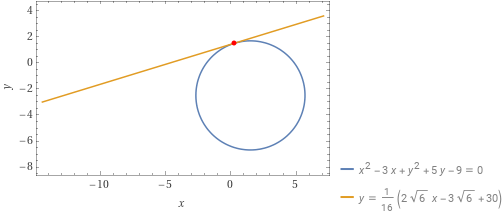

Dato che comunque abbiamo incontrato dei calcoli un po’ scomodi, vediamo se con il metodo della perpendicolarità fra rette le cose migliorano.

Perpendicolarità fra rette. Riprendiamo l’equazione della circonferenza nella forma iniziale:

x^2+y^2-3x+5y-9=0

Calcoliamo le coordinate del suo centro:

x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot(- 3)=\dfrac{3}{2}, \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot 5=-\dfrac{5}{2}

Procediamo con il calcolo del coefficiente angolare della retta passante per {C} e per {P}:

\begin{align*} & m_{CP}=\dfrac{y_P-y_C}{x_P-x_C}=\dfrac{\dfrac{3}{2}-\left(- \dfrac{5}{2}\right)}{\dfrac{3-\sqrt{6}}{2}-\dfrac{3}{2}}=\dfrac{\dfrac{3}{2}+\dfrac{5}{2}}{\dfrac{3-\sqrt{6}-3}{2}}=\\ \\ & =\dfrac{4}{\dfrac{-\sqrt{6}}{2}}=4 \cdot \dfrac{2}{-\sqrt{6}}=-\dfrac{8}{\sqrt{6}} \cdot \dfrac{\sqrt{6}}{\sqrt{6}}=-\dfrac{8\sqrt{6}}{6}=-\dfrac{4}{3}\sqrt{6}\end{align*}

Proseguiamo calcolando il coefficiente angolare della retta tangente cercata:

m=-\dfrac{1}{m_{CP}}=-\dfrac{1}{-\dfrac{4}{3}\sqrt{6}}=\dfrac{3}{4\sqrt{6}}\cdot \dfrac{\sqrt{6}}{\sqrt{6}}=\dfrac{3\sqrt{6}}{24}=\dfrac{1}{8}\sqrt{6}

Ora non resta che sostituire il valore del coefficiente angolare appena ottenuto nell’equazione:

t:y-y_P=m(x-x_P)

ottenendo:

t:y-\dfrac{3}{2}=\dfrac{1}{8}\sqrt{6}\cdot \left( x-\dfrac{3-\sqrt{6}}{2}\right)

ovvero sviluppando i calcoli:

\begin{align*} &y=\dfrac{1}{8}\sqrt{6}\cdot \left( x-\dfrac{3-\sqrt{6}}{2}\right)+\dfrac{3}{2};\\ \\ & y=\dfrac{\sqrt{6}}{8}x-\dfrac{3\sqrt{6}-6}{16}+\dfrac{3}{2};\\ \\ & y=\dfrac{\sqrt{6}}{8}x-\dfrac{3\sqrt{6}}{16}+\dfrac{6}{16}+\dfrac{3}{2}; \\ \\ & y=\dfrac{2\sqrt{6}x-3\sqrt{6}+30}{16};\\ \\ & t: y=\dfrac{1}{16}(2\sqrt{6}x-3\sqrt{6}+30)\end{align*}

Abbiamo così ritrovato correttamente lo stesso risultato del metodo precedente.

Esercizio 3

Determinare l’equazione della retta tangente {t} alla circonferenza di equazione {x^2+y^2-6x-4y+3=0} nel punto {P=(4,5)}.

Utilizziamo per questo esercizio le formule di sdoppiamento. Tenendo conto delle coordinate del punto di tangenza {P}, le sostituzioni da eseguire nell’equazione della circonferenza sono:

x^2 \rightarrow 4x, \qquad y^2\rightarrow 5y, \qquad x\rightarrow \dfrac{x+4}{2}, \qquad y\rightarrow \dfrac{y+5}{2}

Così operando tali sostituzioni otteniamo a partire dall’equazione della circonferenza, che è già in forma canonica:

4x+5y-6 \cdot \dfrac{x+4}{2}-4\cdot\dfrac{y+5}{2}+3=0

Sviluppando i calcoli:

\begin{align*} &4x+5y-3x-12-2y-10+3=0;\\ \\ & t:x+3y-19=0\end{align*}

ovvero in forma esplicita:

t:y=-\dfrac{1}{3}x+\dfrac{19}{3}

Questa è l’equazione della retta tangente alla circonferenza data nel punto {P=(4,5)}.

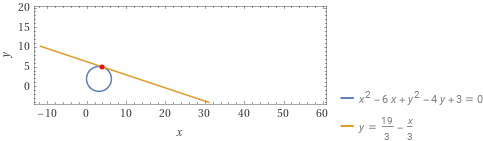
Proseguiamo ora gli esercizi sulla retta tangente ad una circonferenza in un punto con un esercizio nel quale utilizzeremo la relazione di perpendicolarità fra rette.

Esercizio 4

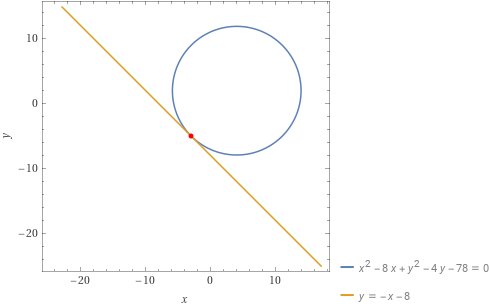
Determinare l’equazione della retta tangente {t} alla circonferenza di equazione {x^2+y^2-8x-4y-78=0} nel punto {P=(-3,-5)}.

Utilizziamo la relazione di perpendicolarità fra rette. Cominciamo calcolando le coordinate del centro della circonferenza:

x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot (-8)=4, \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot (-4)=2

Proseguiamo calcolando il coefficiente angolare della retta passante per i punti {C} e {P}:

m_{CP}=\dfrac{y_P-y_C}{x_P-x_C}=\dfrac{-5-2}{-3-4}=\dfrac{-7}{-7}=1

La retta tangente {t} è perpendicolare alla retta per {C} e {P}. DI conseguenza, per il coefficiente angolare della retta {t} abbiamo:

m=-\dfrac{1}{m_{CP}}=-\dfrac{1}{1}=-1

In conclusione, l’equazione della retta tangente {t} alla circonferenza nel punto {P} è:

\begin{align*} &t: y-y_P=m(x-x_P)\quad  \Rightarrow \quad t:y+5=-1(x+3)\end{align*}

ovvero:

t:y=-x-8

Esercizio 5

Concludiamo questa serie di esercizi sulla retta tangente ad una circonferenza in un suo punto con il seguente, nel quale vedremo dei casi particolari relativi a rette tangenti orizzontali e verticali.

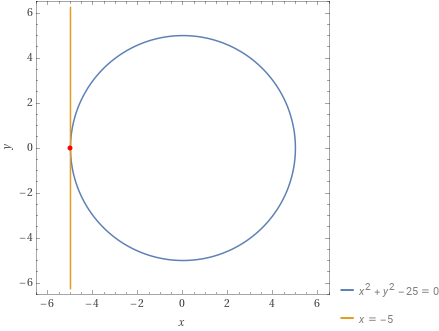
Determinare l’equazione della retta tangente alla circonferenza di equazione {x^2+y^2-25=0} nei punti {P_1=(0,5)} e {P_2=(-5,0)}.

Osserviamo che nell’equazione della circonferenza i coefficienti {a,b,c} sono tutti nulli. Di conseguenza, la circonferenza è centrata nell’origine.

Vediamo come determinare le equazioni delle rette tangenti alla circonferenza rispettivamente nei punti {P_1} e {P_2}.

Formule di sdoppiamento. Scriviamo le formule di sdoppiamento relativamente al punto {P_1=(0,5)}:

x^2 \rightarrow 0 \cdot x, \qquad y^2 \rightarrow 5\cdot y, \qquad x \rightarrow \dfrac{x+0}{2}, \qquad y \rightarrow \dfrac{y+5}{2}

ovvero:

x^2 \rightarrow 0, \qquad y^2 \rightarrow 5y, \qquad x \rightarrow \dfrac{1}{2}x, \qquad y \rightarrow \dfrac{y+5}{2}

Osserviamo che in questo particolare caso, non avendo nell’equazione della circonferenza le quantità {x} e {y}, dobbiamo semplicemente ignorare le sostituzioni relative a tali quantità.

Effettuando le sostituzioni scritte, l’equazione della circonferenza diviene:

5y-25=0

ovvero:

t: y=5

e questa è l’equazione della retta tangente alla circonferenza nel punto {P_1=(0,5)}.

Scriviamo ora le formule di sdoppiamento relativamente al punto {P_2=(-5,0)}:

x^2 \rightarrow -5x, \qquad y^2=0\cdot y, \qquad \dots

Omettiamo le formule di sdoppiamento per i termini in {x} e {y} poiché questi non figurano nell’equazione della circonferenza. Così in questo caso le uniche sostituzioni da eseguire sono:

x^2 \rightarrow -5x, \qquad y^2 \rightarrow 0

Così dall’equazione della circonferenza otteniamo:

-5x-25=0

ovvero:

t:x=-5

e questa è l’equazione della retta tangente alla circonferenza nel punto {P_2=(-5,0)}.

Perpendicolarità fra rette. Vediamo ora come ritrovare le equazioni delle rette tangenti appena scritte utilizzando l’opportuna relazione di perpendicolarità fra rette.

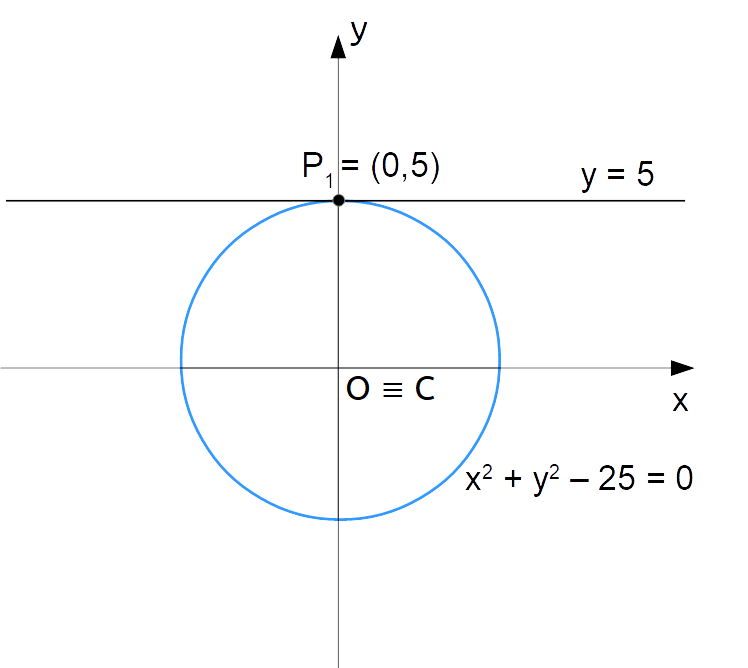
Cominciamo dal punto {P_1=(0,5)}. Anzitutto, essendo la circonferenza centrata nell’origine, il suo centro è {C=(0,0)}, da cui {x_C=0} ed {y_C=0}.

Così per il coefficiente angolare della retta passante per {C} e {P_1} abbiamo:

m_{CP_1}=\dfrac{y_{P_1}-y_C}{x_{P_1}-x_C}=\dfrac{5-0}{0-0} \quad \text{non esiste}

Poiché il denominatore si annulla non possiamo scrivere il coefficiente angolare della retta per {C} e {P_1}. Infatti, poiché le ascisse dei punti {C} e {P_1} hanno lo stesso valore, la retta per {C} e {P_1} è verticale. E per le rette verticali il coefficiente angolare non è definito.

Ma se la retta {r_{CP_1}} è verticale, la tangente alla circonferenza per il punto {P_{1}} dovrà essere necessariamente orizzontale. Ciò per la relazione di perpendicolarità ormai nota fra retta tangente ad una circonferenza in un punto e retta passante per tale punto e per il centro della circonferenza stessa.

Inoltre, la retta tangente oltre ad essere orizzontale passa per il punto {P_1}, che ha ordinata {5}. Di conseguenza, l’equazione della retta tangente sarà:

t_1:y=5

ovvero una retta orizzontale tale da passare per {P_1}.

Quindi, pur non potendo calcolare il coefficiente angolare della retta per {C} e {P_1}, è comunque possibile cavarsela con un po’ di ragionamento, ricordando le definizioni di rette orizzontali e verticali.

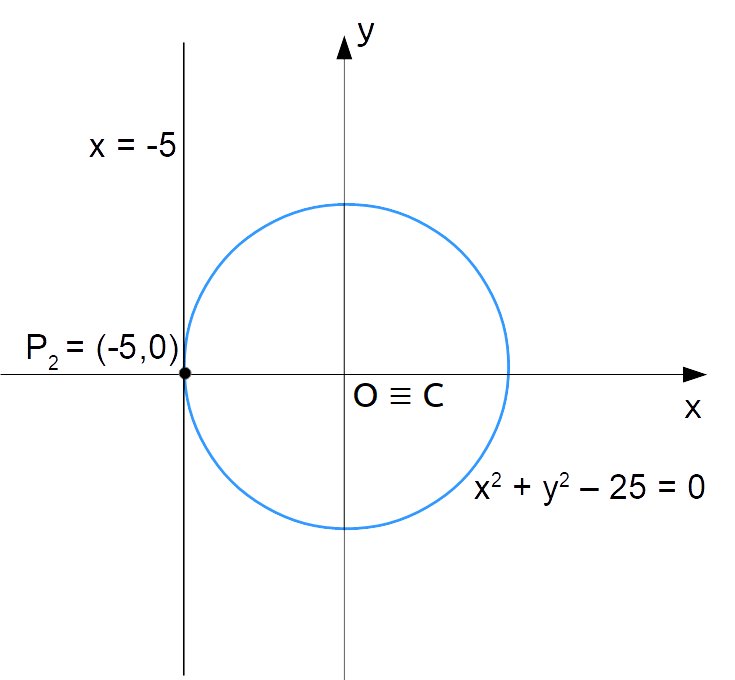
Concludiamo ora con il punto {P_2=(-5,0)}.

Scriviamo il coefficiente angolare della retta passante per {P_2} e per il centro {C} della circonferenza:

m_{CP_2}=\dfrac{y_{P_2}-y_C}{x_{P_2}-x_C}=\dfrac{0-0}{-5-0}=0

Il coefficiente angolare della retta per {C} e {P_2} è nullo. Di conseguenza, la retta per {C} e {P_2} è orizzontale. Infatti, i due punti condividono la stessa ordinata.

Non è dunque possibile ricavare il coefficiente angolare della retta tangente alla circonferenza in {P_2}. Infatti, nell’uguaglianza {m=-\dfrac{1}{m_{CP_2}}} ci ritroveremmo con un denominatore uguale a zero.

Tuttavia, se la retta passante per {C} e {P_2} è orizzontale, per quanto sappiamo la tangente alla circonferenza in {P_2} dovrà necessariamente essere verticale. E inoltre, dato che la retta passa per {P_2}, che ha ascissa {-5}, l’equazione della retta tangente cercata dovrà essere:

t_2:x=-5

ovvero si tratta della retta verticale passante per {P_2}.

Abbiamo così ritrovato con il metodo delle rette perpendicolari gli stessi risultati ottenuti con le formule di sdoppiamento. Tuttavia, in presenza di rette tangenti orizzontali o verticali i ragionamenti da fare con il metodo delle rette perpendicolari richiedono un po’ di attenzione.

Per non confonderci, ricordiamo sempre che una retta orizzontale è della forma:

y=k, \qquad k \in \R \qquad \text{retta orizzontale}

ed è data da punti aventi tutti la stessa ordinata.

Così, una retta orizzontale passante per un dato punto avrà {k} uguale all’ordinata di quello stesso punto.

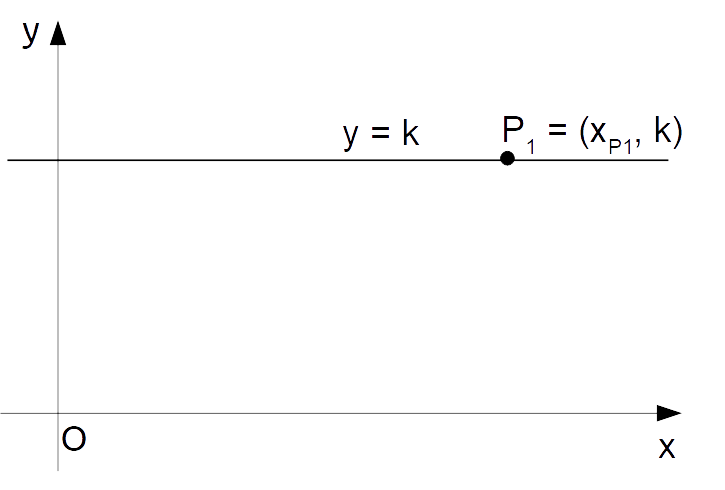
Allo stesso modo, una retta verticale è della forma:

x=k, \qquad k \in \R \qquad \text{retta verticale}

ed è data da punti aventi tutti la stessa ascissa. Così, una retta verticale passante per un dato punto avrà {k} uguale all’ascissa di quello stesso punto.

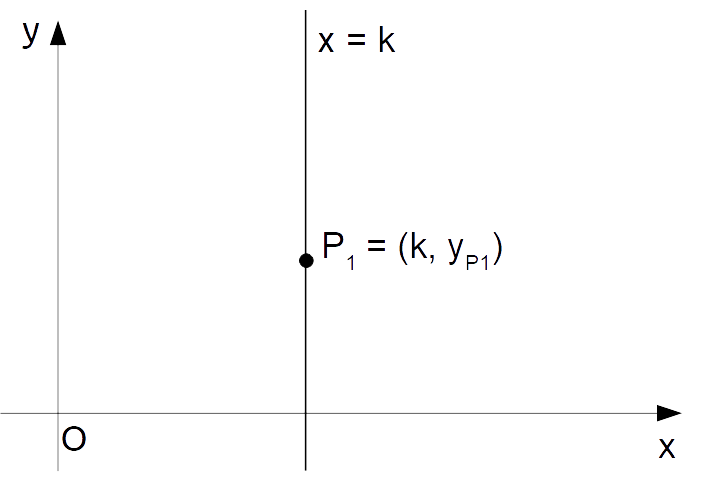
Questi sono i semplici ragionamenti che abbiamo adottato nell’esempio appena visto.

Per quanto riguarda questa serie di esercizi sull’equazione della retta tangente ad una circonferenza in suo punto è tutto. Buono studio a tutti voi con SìMatematica! 🙂