Esercizi sull’equazione della circonferenza

 - 

Esercizi sulla circonferenza (scuole superiori)

In questa scheda vedremo come risolvere gli esercizi sull’equazione della circonferenza, relativi sia all’equazione con centro e raggio, sia all’equazione in forma canonica. Ci occuperemo in particolare di scrivere l’equazione di una circonferenza a partire dalle coordinate del centro e dal raggio, ed inoltre di determinare centro e raggio di una circonferenza a partire dalla sua equazione.

Vedremo poi come passare dall’equazione di una circonferenza con centro e raggio alla corrispondente equazione in forma canonica e viceversa. Nello svolgere gli esercizi sull’equazione della circonferenza avremo modo di constatare che non sempre un’equazione in forma canonica rappresenta una circonferenza. Di conseguenza, prima di ricavare centro e raggio da una presunta equazione in forma canonica di una circonferenza, in generale occorre verificare che l’equazione data corrisponda effettivamente ad una circonferenza reale non degenere, ovvero con raggio positivo non nullo. La verifica è necessaria a meno che il testo dell’esercizio non ci informi già del fatto che siamo di fronte all’equazione di una circonferenza reale non degenere.

Diversamente, un’equazione del tipo con centro e raggio rappresenta sempre una circonferenza reale non degenere. Per cui, se negli esercizi abbiamo una circonferenza della quale è data l’equazione nella forma con centro e raggio, non serve alcuna verifica circa il fatto che la circonferenza sia reale non degenere.

Esercizi sull’equazione della circonferenza in forma canonica e con centro e raggio

Prima parte: esercizi sull’equazione della circonferenza con centro e raggio

Esercizio 1

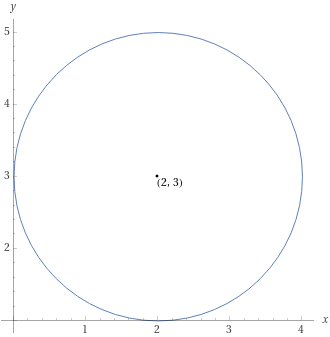
Scrivere l’equazione con centro e raggio di una circonferenza avente centro {C=(2,3)} e raggio {2}.

Poiché il centro della circonferenza è {C=(2,3)}, le coordinate del centro sono rispettivamente {x_C=2} e {y_C=3}. Inoltre, abbiamo come dato {r=2}. Si tratta quindi di sostituire tali valori nell’equazione della circonferenza con centro e raggio:

(x-x_C)^2+(y-y_C)^2=r^2, \qquad \text{con} \: x_C=2, \: y_C=3, \: r=2

Nel nostro caso non abbiamo particolari difficoltà poiché i valori da sostituire sono tutti positivi. Così, dovremo semplicemente mantenere i segni meno davanti ad {x_C} ed {y_C} sostituendo direttamente i valori delle coordinate:

(x-2)^2+(y-3)^2=2^2

Calcolando la potenza al secondo membro otteniamo in conclusione:

(x-2)^2+(y-3)^2=4

E questa è l’equazione con centro e raggio corrispondente alla circonferenza data.

Esercizio 2

Scrivere l’equazione con centro e raggio di una circonferenza avente centro {C=(-2, -3)} e raggio {\sqrt{5}}.

In questo caso dobbiamo prestare attenzione poiché i valori delle coordinate del centro sono negativi. Al fine di evitare errori di segno, conviene fare abbondante uso delle parentesi:

\begin{align*} &(x-x_C)^2+(y-y_C)^2=r^2, \qquad \text{con} \: x_C=-2, \: y_C=-3, \: r=\sqrt{5} \\ \\ & [x-(-2)]^2+[y-(-3)]^2=\left( \sqrt{5}\right)^2\end{align*}

A questo punto, ricordando le regole dell’algebra elementare relative ai segni e calcolando il quadrato al secondo membro otteniamo:

(x+2)^2+(y+3)^2=5

Ricordiamo infatti che sottrarre una quantità negativa equivale a sommare il valore assoluto di tale quantità. Così ad esempio {x-(-2) = x+2}.

Infine per quanto riguarda il secondo membro, se eleviamo al quadrato una quantità sotto radice quadrata rimaniamo semplicemente con la sola quantità all’interno della radice. Così nel nostro caso elevando al quadrato {\sqrt{5}} otteniamo {5}.

Abbiamo quindi scritto in conclusione l’equazione con centro e raggio della circonferenza data.

Proseguiamo ora gli esercizi sull’equazione della circonferenza vedendo in particolare come ricavare le coordinate del centro e la misura del raggio a partire dall’equazione con centro e raggio. Questo è il caso più semplice, ma a breve vedremo anche come ricavare centro e raggio a partire dall’equazione di una circonferenza in forma canonica.

Esercizio 3

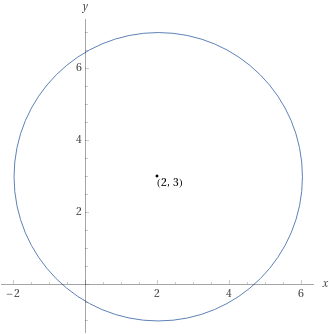
Determinare le coordinate del centro e la misura del raggio della circonferenza di equazione {(x-2)^2+(y-3)^2=16}.

Il punto di partenza è l’equazione con centro e raggio di una generica circonferenza:

(x-x_C)^2+(y-y_C)^2=r^2

Confrontiamola con l’equazione data nel nostro caso:

(x-\underbrace{2}_{x_C})^2+(y-\underbrace{3}_{y_C})^2=\underbrace{16}_{r^2}

Dal confronto è immediato stabilire che abbiamo {x_C=2}, {y_C=3} ed {r^2=16}. Come possiamo vedere, infatti, i termini dei quadrati al primo membro sono tutti separati tra loro da un segno meno, esattamente come nell’equazione con centro e raggio di una circonferenza generica. Così, per ricavare le coordinate del centro basta semplicemente considerare i valori numerici che si trovano di seguito ai simboli di sottrazione.

Per il raggio, essendo {r^2=16} abbiamo {r=\sqrt{16}=4}.

Quindi in conclusione la circonferenza in esame ha centro {C=(2,3)} e raggio {r=4}.

Esercizio 4

Determinare coordinate del centro e raggio della circonferenza di equazione {(x-5)^2+(y+7)^2=25}.

Qui occorre prestare attenzione. Se confrontiamo l’equazione con centro e raggio di una circonferenza generica, ovvero:

(x-x_C)^2+(y-y_C)^2=r^2

con l’equazione data:

(x-5)^2+(y+7)^2=25

ci accorgiamo immediatamente che i termini del secondo quadrato al primo membro sono separati tra loro da un segno più, e non da un segno meno come nella forma generica dell’equazione con centro e raggio.

Poiché dobbiamo necessariamente ricondurci alla situazione dell’equazione con centro e raggio di una circonferenza generica, procediamo riscrivendo l’equazione del caso in esame come segue:

(x-\underbrace{5}_{x_C})^2+[y-(\underbrace{-7}_{y_C})]^2=25

In questo modo l’equazione è equivalente a quella data (infatti {y-(-7)} è uguale a {y+7}) ed abbiamo ora, in entrambi i quadrati, dei termini separati tra loro da un simbolo di sottrazione.

Così i valori che si ricavano dall’equazione sono:

x_C=5, \quad y_C=-7, \quad r^2=25

e quindi in conclusione per la circonferenza data si ha:

C=(5,-7), \quad r=\sqrt{25}=5

Seconda parte: esercizi sull’equazione della circonferenza in forma canonica

Vediamo ora degli esercizi sull’equazione della circonferenza relativi all’equazione in forma canonica. Mostreremo in particolare:

• come scrivere l’equazione canonica di una circonferenza a partire dal centro e dal raggio, e viceversa come ricavare tali dati a partire dall’equazione canonica di una circonferenza (verificando ove necessario che si tratti dell’equazione di una circonferenza reale non degenere);
• come passare dall’equazione con centro e raggio all’equazione in forma canonica;
• infine, come passare dall’equazione canonica di una circonferenza all’equazione con centro e raggio.

Esercizio 5

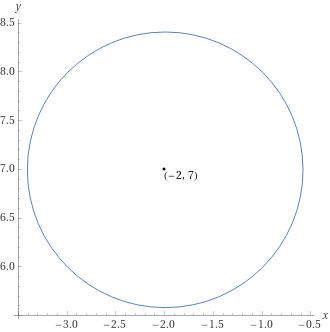
Scrivere l’equazione in forma canonica di una circonferenza avente centro {C=(-2,7)} e raggio {\sqrt{2}}.

Ricordiamo che l’equazione in forma canonica di una circonferenza è data da:

x^2+y^2+ax+by+c=0

Se ci vengono dati le coordinate del centro e il raggio, è immediato ricavare i coefficienti {a,b,c} necessari a scrivere l’equazione mediante le seguenti formule:

a=-2x_C, \quad b=-2y_C, \quad c=x_C^2+y_C^2-r^2

Nel nostro caso abbiamo:

C=(-2, 7) \quad \Rightarrow \quad x_C=-2, \: y_C=7

e quindi:

a=-2 \cdot x_C=-2 \cdot (-2)=4, \quad b=-2 \cdot y_C=-2 \cdot 7 = -14

ed infine per il termine noto {c}:

c=x_C^2+y_C^2-r^2=(-2)^2+7^2-(\sqrt{2})^2=4+49-2=51

Così in conclusione sostituendo i valori appena calcolati per {a,b,c} nell’equazione {x^2+y^2+ax+by+c=0} otteniamol’equazione in forma canonica della circonferenza in esame:

x^2+y^2+4x-14y+51=0

Esercizio 6

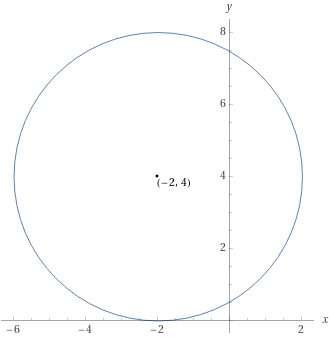
Verificare che l’equazione {x^2+y^2+4x-8y+4=0} corrisponde ad una circonferenza reale non degenere ed eventualmente determinare centro e raggio della circonferenza.

L’equazione data è:

x^2+y^2+4x-8y+4=0

Dal confronto con l’equazione in forma canonica di una generica circonferenza:

x^2+y^2+ax+by+c=0

otteniamo nel nostro caso:

a=4, \: b=-8, \: c=4

Ora, per verificare che una circonferenza con equazione data in forma canonica sia reale non degenere basta sostituire i valori dei coefficienti {a,b,c} nella relazione:

\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0

Si ha nel nostro caso:

\dfrac{4^2}{4}+\dfrac{(-8)^2}{4}-4=\dfrac{16+64-16}{4}=16>0 \quad \text{OK}

La circonferenza corrispondente all’equazione data è dunque reale non degenere. Osserviamo che in alternativa a tale metodo di verifica, è anche possibile vedere se calcolando il raggio si ottiene una radice quadrata di una quantità negativa (evidentemente impossibile nei reali). Se ciò avviene, la circonferenza non è reale. Diversamente, si otterrà un valore reale del raggio e diremo che la circonferenza è reale. Se tale valore è inoltre diverso da zero la circonferenza sarà pure non degenere.

Proseguendo, a partire dai coefficienti {a,b,c} dell’equazione in forma canonica di una circonferenza, è possibile ricavare centro e raggio mediante le seguenti formule:

x_C=-\dfrac{1}{2}a, \: y_C=-\dfrac{1}{2}b, \: r=\sqrt{x_C^2+y_C^2-c} 

Quindi si tratterà anzitutto di ricavare le coordinate del centro della circonferenza con le prime due formule, per poi ricavare la misura del raggio grazie all’ultima formula:

\begin{align*} &x_C=-\dfrac{1}{2}a=-\dfrac{1}{2}\cdot 4 = -2, \quad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2}\cdot(-8)=4,\\ \\ & r=\sqrt{x_C^2+y_C^2-c}=\sqrt{(-2)^2+4^2-4}=\sqrt{4+16-4}=\sqrt{16}=4\end{align*}

Nota: nella precedente verifica per la realtà della circonferenza, il valore che si ottiene, se maggiore di zero, è il quadrato del raggio. Dunque avremmo potuto semplicemente limitarci a calcolare il raggio immediatamente dopo aver eseguito la verifica.

Per cui in conclusione l’equazione data rappresenta una circonferenza reale non degenere avente i seguenti dati:

C=(-2, 4), \quad r=4

Proseguiamo ancora gli esercizi sull’equazione della circonferenza con il seguente.

Esercizio 7

Calcolare centro e raggio, se possibile, della circonferenza di equazione {2x^2+2y^2-6x-10y+6=0}.

Prima di tutto, osserviamo che l’equazione di partenza non è in forma canonica. Siamo piuttosto di fronte ad un’equazione nella forma più generale:

Ax^2+Ay^2+Cx+Dy+E=0

Per ricondurci alla forma canonica, dobbiamo dividere tutti i termini al primo membro dell’equazione di partenza per {A}. In tal modo infatti i coefficienti dei termini in {x^2} ed {y^2} diventeranno uguali a {1}, come effettivamente richiesto dalla forma canonica dell’equazione di una circonferenza. Nel nostro caso abbiamo:

\dfrac{2}{2}x^2+\dfrac{2}{2}y^2-\dfrac{6}{2}x-\dfrac{10}{2}y+\dfrac{6}{2}=0

ovvero:

x^2+y^2-3x-5y+3=0

e di conseguenza i valori dei coefficienti {a,b,c} sono:

a=-3, \: b=-5, \: c=3

Ora l’equazione è in forma canonica, e possiamo verificare se siamo in presenza di una circonferenza reale non degenere. Verifichiamo la corrispondente condizione:

\dfrac{a^2}{4}+\dfrac{b^2}{4}-c=\dfrac{(-3)^2}{4}+\dfrac{(-5)^2}{4}-3=\dfrac{9+25-12}{4}=\dfrac{11}{2}> 0

Il valore ottenuto è positivo non nullo, per cui la circonferenza è reale non degenere. Il raggio della circonferenza si può ottenere direttamente come:

r=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}-c}=\sqrt{\dfrac{11}{2}}

Concludiamo calcolando le coordinate del centro della circonferenza a partire dai coefficienti {a, b}:

\small x_C=-\dfrac{1}{2}a=-\dfrac{1}{2}\cdot(-3)=\dfrac{3}{2}, \quad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot (-5)=\dfrac{5}{2}

Così in conclusione la circonferenza ha centro {C=\left( \dfrac{3}{2}, \dfrac{5}{2}\right)} e raggio {r=\sqrt{\dfrac{11}{2}}}.

Metodo alternativo. In alternativa è anche possibile determinare il centro e il raggio della circonferenza a partire dalla sua equazione in forma canonica utilizzando il metodo del completamento dei quadrati. Il punto di partenza è sempre dato da un’equazione in forma canonica (quindi con coefficienti dei termini in {x^2} ed {y^2} unitari) verificata essere relativa ad una circonferenza reale non degenere.

Nel nostro caso l’equazione da considerare è ancora quella in forma canonica:

x^2+y^2-3x-5y+3=0

e non l’equazione di partenza. Infatti, anche volendo utilizzare il metodo del completamento dei quadrati è importante che l’equazione sia in forma canonica. Diversamente, come mostreremo alla fine della lezione, il procedimento risulterebbe più complicato.

Vediamo quindi come si usa il metodo del completamento dei quadrati per la circonferenza. Anzitutto, riordiniamo i termini in modo da avere termini che condividono la stessa lettera uno di seguito all’altro:

x^2-3x+y^2-5y+3=0

Ora portiamo il termine noto al secondo membro:

\underbrace{x^2-3x}_{\substack{\text{primo quadrato} \\ \text{incompleto}}}+\underbrace{y^2-5y}_{\substack{\text{secondo quadrato} \\ \text{incompleto}}}=-3

A questo punto, le quantità {x^2-3x} e {y^2-5y} sono i quadrati da completare. In particolare, nella quantità:

x^2-3x

il termine {-3x} è il doppio prodotto:

-3x=2 \cdot \left( -\dfrac{3}{2}\right) \cdot x

Quindi il quadrato da completare è il quadrato del binomio {x-\dfrac{3}{2}}. Di conseguenza, nello sviluppo di tale quadrato dovrà necessariamente comparire il quadrato di {-\dfrac{3}{2}}, ovvero {\dfrac{9}{4}}. E questo è il termine mancante per completare il primo quadrato di un binomio. Per cui nell’equazione abbiamo intanto:

\underbrace{x^2-3x+\boxed{\dfrac{9}{4}}}_{\substack{\text{primo quadrato} \\ \text{di un binomio}}}+y^2-5y=-3+\boxed{\dfrac{9}{4}}

Osserviamo che la quantità {\dfrac{9}{4}}, utilizzata per completare il primo quadrato, deve essere sommata anche al secondo membro. Ciò discende immediatamente dal primo principio di equivalenza delle equazioni.

Allo stesso modo, completiamo anche il quadrato relativo alla quantità {y^2-5y}, nella quale riconosciamo il seguente doppio prodotto:

-5y=2 \cdot \left( -\dfrac{5}{2}\right) \cdot y

Quindi il termine necessario a completare il secondo quadrato è in questo caso {\left( -\dfrac{5}{2}\right)^2}, ovvero {\dfrac{25}{4}}:

\underbrace{x^2-3x+\boxed{\dfrac{9}{4}}}_{\substack{\text{primo quadrato} \\ \text{di un binomio}}}+\underbrace{y^2-5y+\boxed{\dfrac{25}{4}}}_{\substack{\text{secondo quadrato} \\ \text{di un binomio}}}=-3+\boxed{\dfrac{9}{4}}+\boxed{\dfrac{25}{4}}

Ancora una volta, ricordiamo di sommare la quantità necessaria a completare il quadrato anche al secondo membro.

Ora non resta che scomporre in fattori i quadrati dei binomi, ovvero riscriverli nelle forme {(x+ \dots)^2} e {(y+ \dots)^2}. Per fare questo non abbiamo problemi. Basta ricordare quali termini abbiamo elevato al quadrato per ricavare le quantità necessarie a completare i quadrati, facendo attenzione ai segni. Così abbiamo:

\left( x-\dfrac{3}{2}\right)^2+\left( y-\dfrac{5}{2}\right)^2=-3+\dfrac{9}{4}+\dfrac{25}{4}

Ora non resta che eseguire la somma algebrica al secondo membro:

\left( x-\dfrac{3}{2}\right)^2+\left( y-\dfrac{5}{2}\right)^2=\dfrac{11}{2}

In conclusione osserviamo che l’equazione ottenuta è l’equazione di una circonferenza con centro e raggio. E quindi, confrontandola con l’equazione con centro e raggio di una circonferenza generica:

(x-x_C)^2+(y-y_C)^2=r^2

otteniamo:

x_C=\dfrac{3}{2}, \quad y_C=\dfrac{5}{2}, \quad r=\sqrt{\dfrac{11}{2}}

Terza parte: come passare dall’equazione con centro e raggio di una circonferenza all’equazione in forma canonica e viceversa

Proseguiamo gli esercizi sull’equazione della circonferenza mostrando come passare dall’equazione con centro e raggio alla corrispondente equazione in forma canonica e, ove possibile, il viceversa.

Esercizio 8

Riscrivere in forma canonica la seguente equazione di una circonferenza con centro e raggio:{(x-1)^2+\left( y-\dfrac{1}{2}\right)^2=3}.

Dall’equazione data:

(x-1)^2+\left( y-\dfrac{1}{2}\right)^2=3

è immediato ricavare le coordinate del centro della circonferenza e la misura del suo raggio:

x_C=1, \: y_C=\dfrac{1}{2}, \: r=\sqrt{3}

Perché il raggio è {\sqrt{3}}? Ricordiamo sempre che il secondo membro dell’equazione di una circonferenza con centro e raggio è il quadrato del raggio. Di conseguenza, il raggio sarà la radice quadrata del secondo membro.

Ora che disponiamo delle coordinate del centro e della misura del raggio della circonferenza, possiamo ricavare i coefficienti {a,b,c} necessari a scrivere l’equazione in forma canonica della circonferenza. Allo scopo possiamo infatti utilizzare le seguenti formule:

a=-2x_C; \quad b=-2y_C; \quad c=x_C^2+y_C^2-r^2

E quindi nel nostro caso abbiamo:

\begin{align*} & a=-2 x_C= -2 \cdot 1=-2;\\ \\ & b=-2y_C=-2 \cdot \dfrac{1}{2} =-1;\\ \\ & c=x_C^2+y_C^2-r^2=1^2+\left( \dfrac{1}{2}\right)^2-(\sqrt{3})^2 =\dfrac{ 4+1-12}{4}=-\dfrac{7}{4}\end{align*}

Così in conclusione l’equazione di partenza può essere riscritta in forma canonica come:

\begin{align*} &x^2+y^2+ax+by+c=0 \quad \text{con} \quad a=-2, \: b=-1, \: c=-\dfrac{7}{4} \\ \\ & \Rightarrow x^2+y^2-2x-y-\dfrac{7}{4}=0\end{align*}

Metodo alternativo. Se non si ricordano le formule necessarie, per passare dall’equazione con centro e raggio all’equazione in forma canonica di una circonferenza è anche possibile sviluppare i quadrati di binomi:

\begin{align*} &(x-1)^2+\left( y-\dfrac{1}{2}\right)^2=3; \\ \\ & x^2-2x+1+y^2-y+\dfrac{1}{4}=3;\\ \\ & x^2+y^2-2x-y+1+\dfrac{1}{4}-3=0; \\ \\ & x^2+y^2-2x-y+\dfrac{4+1-12}{4}=0;\\ \\ & x^2+y^2-2x-y-\dfrac{7}{4}=0\end{align*}

Anche in questo modo siamo comunque arrivati all’equazione in forma canonica della circonferenza data. Osserviamo che, una volta calcolati i quadrati dei binomi, dobbiamo procedere portando tutto al primo membro, riordinando opportunamente i termini, e quindi sommando tra loro i soli termini noti (i numeri privi di lettere).

Esercizio 9

Riscrivere nella forma centro e raggio la seguente equazione di una circonferenza (reale non degenere) data in forma canonica:{x^2+y^2-2x+6y-15=0}

Il testo già afferma che l’equazione data effettivamente corrisponde ad una circonferenza reale non degenere, per cui non serve alcuna verifica.

Per scrivere l’equazione con centro e raggio noti, evidentemente abbiamo bisogno delle coordinate del centro e della misura del raggio della circonferenza data.

Dall’equazione fornita dal testo:

x^2+y^2-2x+6y-15=0

ricaviamo:

a=-2, \: b=6, \: c=-15

Da tali coefficienti è immediato ricavare centro e raggio della circonferenza grazie alle formule che già conosciamo:

\begin{align*} & x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot (-2)=1; \quad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2}\cdot6=-3; \\ \\ & r=\sqrt{x_C^2+y_C^2-c}=\sqrt{1^2+(-3)^2-(-15)}=\sqrt{1+9+15}=\\ \\ & =\sqrt{25}=5\end{align*}

Disponendo a questo punto delle coordinate {x_C} e {y_C} e del raggio {r}, basta sostituire i corrispondenti valori nell’equazione con centro e raggio di una generica circonferenza:

(x-x_C)^2+(y-y_C)^2=r^2

ottenendo in conclusione l’equazione cercata:

(x-1)^2+[y-(-3)]^2=5^2

ovvero:

(x-1)^2+(y+3)^2=25

Metodo alternativo. Come ormai sappiamo in alternativa è possibile utilizzare il metodo del completamento dei quadrati. Riprendiamo l’equazione di partenza:

x^2+y^2-2x+6y-15=0

Riordiniamo i termini in modo da scrivere i termini che contengono la stessa lettera uno di seguito all’altro:

x^2-2x+y^2+6y-15=0

Portiamo il termine noto al secondo membro:

x^2-2x+y^2+6y=15

Completiamo i quadrati, ricordandoci che le quantità che utilizziamo per completare i quadrati vanno sommate anche al secondo membro:

x^2-2x+1+y^2+6y+9=15+1+9

Ora, prima di eseguire le somme, scomponiamo in fattori i quadrati al primo membro:

(x-1)^2+(y+3)^2=15+1+9

A questo punto eseguiamo la somma al secondo membro:

(x-1)^2+(y+3)^2=25

Abbiamo così ottenuto anche con questo metodo l’equazione con centro e raggio desiderata.

Esercizio 10

Occupiamoci ora dell’ultimo di questa serie di esercizi sull’equazione della circonferenza.

Riscrivere nella forma con centro e raggio la seguente equazione di una circonferenza reale non degenere: {2x^2+2y^2+4x-4y-25=0}Ricavare inoltre le coordinate del centro e la misura del raggio della circonferenza.

Prestiamo attenzione al fatto che l’equazione non è data in forma canonica, ma nella forma:

Ax^2+Ay^2+Bx+Cy+D=0, \qquad A \neq 1

Di conseguenza, il primo passo consiste nel ricondurre l’equazione data alla forma canonica:

x^2+y^2+ax+by+c=0

ove i coefficienti dei termini di secondo grado sono entrambi uguali ad {1}.

Per fare ciò basta dividere per {A} tutti i termini dell’equazione di partenza. Nel nostro caso. avendo {A=2}:

\dfrac{2}{2}x^2+\dfrac{2}{2}y^2+\dfrac{4}{2}x-\dfrac{4}{2}y-\dfrac{25}{2}=0

e quindi:

x^2+y^2+2x-2y-\dfrac{25}{2}=0

Ora, per ricavare centro e raggio della circonferenza utilizziamo ad esempio il metodo del completamento dei quadrati. L’opportunità dell’utilizzo di tale metodo è in questo caso data dal fatto che i termini {2x} e {-2y} rappresentano dei doppi prodotti con fattori facilmente riconoscibili.

Cominciamo mettendo opportunamente in ordine i termini al primo membro e portando inoltre il termine noto al secondo membro:

x^2+2x+y^2-2y=\dfrac{25}{2}

Completiamo i quadrati:

x^2+2x+1+y^2-2y+1=\dfrac{25}{2}+1+1

Come al solito, abbiamo sommato le quantità utilizzate per completare i quadrati anche al secondo membro. Non dimentichiamo mai questo passaggio.

Stiamo ora attenti a non eseguire nessuna somma al primo membro. Eseguiamo invece la somma (algebrica) al secondo membro:

x^2+2x+1+y^2-2y+1=\dfrac{29}{2}

A questo punto scomponiamo in fattori ciascun quadrato (attenzione ai segni):

(x+1)^2+(y-1)^2=\dfrac{29}{2}

Abbiamo così ottenuto l’equazione con centro e raggio della circonferenza data. Dal confronto con l’equazione con centro e raggio di una circonferenza generica, ovvero:

(x-x_C)^2+(y-y_C)^2=r^2

otteniamo in conclusione (attenzione ai segni):

\small x_C=-1, \quad y_C=1, \quad r^2=\dfrac{29}{2} \quad \Rightarrow \quad r=\sqrt{\dfrac{29}{2}}=\dfrac{\sqrt{29}}{\sqrt{2}}\cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{\sqrt{58}}{2}

Abbiamo così terminato questa serie di esercizi sull’equazione della circonferenza.

Conclusioni

Prima di salutarci, vogliamo soffermarci brevemente sull’importanza di riscrivere sempre l’equazione di una circonferenza data nella forma {Ax^2+Ay^2+Bx+Cy+D=0} con {A \neq 1} in forma canonica. Riprendiamo ad esempio l’equazione data nell’ultimo esempio, relativa ad una circonferenza reale non degenere:

2x^2+2y^2+4x-4y-25=0

Volendo risalire al centro e al raggio utilizzando le formule, dobbiamo stare attenti al fatto che i coefficienti dei termini in {x} e {y} ed il termine noto nell’equazione in questa forma non rappresentano i coefficienti {a,b,c} da utilizzarsi nelle formule. E’ dunque obbligatorio ricondurre alla forma canonica l’equazione in modo da disporre dei coefficienti {a,b,c} necessari ad utilizzare le formule per centro e raggio.

Non è invece obbligatorio ricondurre l’equazione alla forma canonica nel caso in cui si utilizzi il metodo del completamento dei quadrati, ma ciò è fortemente consigliato. Infatti, nel caso dell’equazione in forma {Ax^2+Ay^2+Bx+Cy+D=0} con {A \neq 1}, il metodo del completamento dei quadrati diviene più scomodo, aumentando la possibilità di incorrere in spiacevoli errori.

Proviamo comunque ad utilizzare il metodo del completamento dei quadrati senza ricondurci alla forma canonica. In tal modo, potremo renderci conto delle difficoltà che derivano da una tale scelta.

Riordiniamo i termini come segue, portando il termine noto al secondo membro:

2x^2+4x+2y^2-4y=25

Ora completiamo i quadrati, utilizzando temporaneamente dei simboli:

2x^2+4x+\square+2y^2-4y+\triangle=25+\square+\triangle

Il doppio prodotto del primo quadrato incompleto è {4x}. Osservando inoltre che il termine {2x^2} può essere visto come il quadrato di {\sqrt{2}x}, abbiamo

4x=2\cdot \sqrt{2} \cdot\sqrt{2}x

Di conseguenza un termine nel quadrato del binomio corrispondente è {\sqrt{2}}, e quindi per completare il quadrato abbiamo bisogno della quantità {(\sqrt{2})^2}, ovvero 2:

2x^2+4x+2+2y^2-4y+\triangle=25+2+\triangle

Nel secondo quadrato incompleto, il doppio prodotto è {-4y}. Inoltre, il termine {2y^2} può essere visto come il quadrato di {\sqrt{2}y}:

-4y=2 \cdot \sqrt{2}y \cdot (-\sqrt{2})

Così per il quadrato del binomio corrispondente abbiamo il termine {-\sqrt{2}}, e quindi la quantità necessaria per completare il quadrato è {(-\sqrt{2})^2}, ovvero {2}:

2x^2+4x+2+2y^2-4y+2=25+2+2

Ora sommiamo i termini soltanto al secondo membro:

2x^2+4x+2+2y^2-4y+2=29

Scomponiamo in fattori i quadrati al primo membro, prestando attenzione ai segni:

(\sqrt{2}x+\sqrt{2})^2+(\sqrt{2}y-\sqrt{2})^2=29

Tuttavia, non siamo ancora arrivati alla forma con centro e raggio. Infatti, i termini dei coefficienti in {x} ed {y} nei binomi sono diversi da {1}. Per ricondurre l’equazione alla forma desiderata, eseguiamo nei binomi i seguenti raccoglimenti:

[\sqrt{2}(x+1)]^2+[\sqrt{2}(y-1)]^2=29

da cui, ricordando la regola della potenza di un prodotto:

2(x+1)^2+2(y-1)^2=29

Dividiamo infine tutti i termini per {2}, nel seguente modo:

\dfrac{2(x+1)}{2}^2+\dfrac{2(y-1)^2}{2}=\dfrac{29}{2}

ottenendo, eseguendo le semplificazioni al primo membro:

(x+1)^2+(y-1)^2=\dfrac{29}{2}

Abbiamo così ritrovato l’equazione con centro e raggio della circonferenza, ma con molta più fatica! Infatti, nel completare i quadrati ci siamo ritrovati con delle quantità irrazionali.

Tuttavia, tenendo conto dei raccoglimenti che abbiamo dovuto eseguire, è in generale possibile applicare più convenientemente il metodo del completamento dei quadrati all’equazione di una circonferenza non in forma canonica come segue. Riprendiamo ancora l’equazione di partenza:

2x^2+2y^2+4x-4y-25=0

Ordiniamo come al solito i termini e portiamo il termine noto al secondo membro:

2x^2+4x+2y^2-4y=25

Ora eseguiamo i seguenti raccoglimenti parziali:

2(x^2+2x)+2(y^2-2y)=25

A questo punto potremmo completare i quadrati all’interno delle parentesi tonde, ma attenzione. Seguendo tale metodo risulterebbe più complicato lavorare sul secondo membro. Procediamo piuttosto dividendo tutti i termini dell’equazione per {2}, nel seguente modo:

\dfrac{2(x^2+2x)}{2}+\dfrac{2(y^2-2y)}{2}=\dfrac{25}{2}

ottenendo quindi:

x^2+2x+y^2-2y=\dfrac{25}{2}

A questo punto possiamo completare i quadrati:

x^2+2x+1+y^2-2y+1=\dfrac{25}{2}+1+1

da cui:

(x+1)^2+(y-1)^2=\dfrac{29}{2}

ritrovando correttamente l’equazione della circonferenza in esame.

Quindi, se scegliamo di utilizzare il metodo del completamento dei quadrati senza ricondurre l’equazione della circonferenza alla forma canonica, è importante quantomeno eseguire dei raccoglimenti parziali sul primo membro dell’equazione, come mostrato. Tuttavia, il consiglio è sempre quello di ricondurre l’equazione alla forma canonica, per poi applicare il metodo.

Infine, il metodo del completamento dei quadrati può tornare comodo, ma rispetto all’utilizzo delle formule dirette può risultare un po’ macchinoso. Per cui, sulla scelta del metodo risolutivo da utilizzare per gli esercizi sulla circonferenza vi consigliamo di orientarvi anche in base alle indicazioni del vostro insegnante e/o libro di testo.

Ora è davvero tutto. Per qualsiasi dubbio vi consigliamo la rilettura della lezione teorica correlata. Un saluto a tutti voi e buon proseguimento con SìMatematica!