Come si calcola la diagonale del quadrato? Più in generale cos’è la diagonale del quadrato? Con quali formule è possibile calcolare la diagonale di un quadrato a partire dalla misura del lato, dall’area oppure dal perimetro? Potreste fornire degli esempi di utilizzo delle formule?
Con il termine diagonale del quadrato ci riferiamo ad uno dei segmenti che uniscono tra loro due vertici non consecutivi del quadrato. In particolare in un quadrato abbiamo due diagonali, e queste sono tra loro congruenti (ovvero hanno la stessa lunghezza o misura).
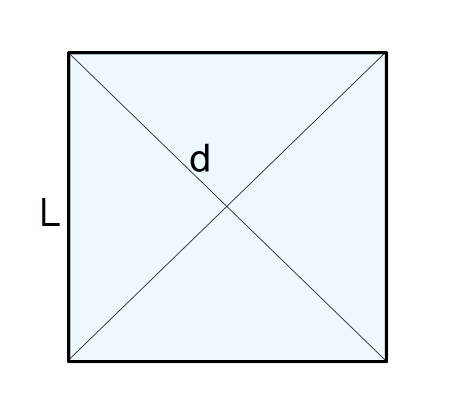
La diagonale del quadrato si calcola moltiplicando la misura del lato per la radice di {2}. Abbiamo così la formula:
d= L \cdot \sqrt{2}La formula si giustifica immediatamente ricordando il teorema di Pitagora e impostando una semplice proporzione. Consideriamo un quadrato avente lato {L} di misura pari a {1}:
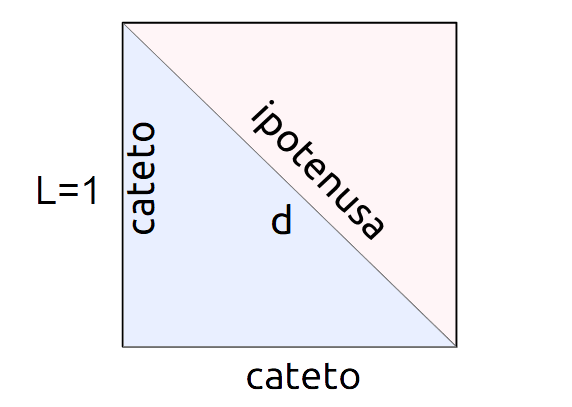
Come possiamo vedere dalla figura, il quadrato può essere visto come l’unione di due triangoli rettangoli aventi cateti tutti di misura pari a {1}. Osserviamo che i due triangoli condividono la stessa ipotenusa, che è proprio la diagonale del quadrato. Così, poiché per il teorema di Pitagora la misura dell’ipotenusa è uguale alla radice della somma dei quadrati dei cateti, possiamo scrivere:
d= \sqrt{1^2+1^2}=\sqrt{2}Ora, due triangoli rettangoli aventi ciascuno i cateti uguali tra loro sono necessariamente simili. Per cui se un quadrato di lato {1} ha diagonale di misura pari a {\sqrt{2}}, la misura della diagonale del quadrato avente lato {L} è ottenibile impostando la seguente proporzione:
1: \sqrt{2}=L:dUguagliando il prodotto dei medi e il prodotto degli estremi:
1 \cdot d = \sqrt{2} \cdot L \quad \Rightarrow \quad d =L \cdot \sqrt{2} e ritroviamo la precedente formula.
Dovendo calcolare la misura della diagonale a partire dall’area o dal perimetro nessun problema: basterà ricavare la misura del lato e quindi grazie alla precedente formula potremo ricavare la diagonale. E’ comunque anche possibile utilizzare delle formule più immediate, come vedremo tra un istante.
Formule della diagonale del quadrato
Vediamo subito quali sono le formule per ricavare la diagonale del quadrato. Oltre alla prima formula già vista:
\boxed{d = L \cdot \sqrt{2} }abbiamo anche le formule:
\boxed{d = \sqrt{2 \cdot A}} ; \qquad \boxed{d= \dfrac{P \cdot \sqrt{2}}{4}}le quali consentono di ricavare la diagonale rispettivamente a partire dall’area e dal perimetro del quadrato. Ma come già anticipato, non è strettamente necessario ricordare tutte e tre le formule.
Infatti, ricordiamo che il perimetro di un quadrato è dato dalla somma delle misure di tutti i suoi lati, ovvero quattro volte la misura dei lati:
P=4 \cdot L
Di conseguenza dato il perimetro è possibile ricavare il lato del quadrato:
L= \dfrac{P}{4}Inoltre, l’area del quadrato si ottiene invece moltiplicando il lato per sé stesso:
A=L \cdot L = L^2
Anche in questo caso, a partire dall’area è possibile ricavare il lato del quadrato:
L=\sqrt{A}In pratica abbiamo estratto la radice quadrata di entrambi i membri della formula {A=L^2}.
Osserviamo quindi che a partire dall’area oppure dal perimetro del quadrato è possibile ricavare la misura del lato. Di conseguenza per il calcolo della diagonale non è necessario ricordare tutte e tre le precedenti formule, ma basta ricordare soltanto la prima formula:
d = L \cdot \sqrt{2} Infatti potremo in generale ricavare il lato {L} dai dati di partenza che abbiamo.
Esempi
Vediamo ora degli esempi pratici sul calcolo della diagonale del quadrato.
Esempio 1
Calcolare la misura della diagonale di un quadrato di lato {20 \text{cm}}.
Abbiamo, applicando la prima formula:
d=L \cdot \sqrt{2} = 20 \text{cm} \cdot \sqrt{2} \approx 28, 28 \text{cm}Esempio 2
Calcolare la misura della diagonale di un quadrato avente area {400 \text{m}^2}.
Risolviamo il problema utilizzando ancora la prima formula. Il dato che ci manca è la misura del lato del quadrato. Ma poiché disponiamo dell’area, possiamo ricavarla come segue:
L= \sqrt{A} = \sqrt{400 \text{m}^2} = 20 \text{m}Ora ci siamo. Possiamo calcolare la diagonale utilizzando la misura del lato appena ricavata:
d = L \cdot \sqrt{2} = 20 \text{m} \cdot \sqrt{2} \approx 28,28 \text{m} E siamo arrivati al risultato finale. In alternativa, avremmo potuto direttamente utilizzare la seconda formula:
d = \sqrt{2 \cdot A} = \sqrt{2 \cdot 400 \text{m}^2}=\sqrt{800 \text{m}^2} \approx 28,28 \text{m}Esempio 3
Calcolare la diagonale di un quadrato avente perimetro {P = 160 \text{cm}}.
Vediamo anche in questo caso come ricavare la misura della diagonale utilizzando la prima formula. Dobbiamo anzitutto ricavare la misura del lato a partire dal perimetro:
L=\dfrac{P}{4}=\dfrac{160 \text{cm}}{4}=40 \text{cm}A questo punto possiamo ricavare la diagonale:
d = L \cdot \sqrt{2} = 40 \text{cm} \cdot \sqrt{2} \approx 56,57 \text{cm}ed abbiamo concluso.
Osserviamo che avremmo potuto in alternativa utilizzare direttamente la terza formula:
d = \dfrac{P \cdot \sqrt{2}}{4}={\dfrac{160 \text{cm} \cdot \sqrt{2}}{4}} \approx \dfrac{226,27}{4} \approx 56,57 \text{cm}Come ricavare le formule della diagonale del quadrato
A partire dalla prima formula:
d= L \cdot \sqrt{2} come possiamo ricavare le altre due? Basta sostituire ad {L} la corrispondente espressione in funzione del dato di partenza che abbiamo. Ad esempio, se ci viene data l’area del quadrato, sappiamo che {L=\sqrt{A}}. Sostituendo nella prima formula alla lettera {L} l’espressione {\sqrt{A}}:
d = L \cdot \sqrt{2} = \sqrt{A} \cdot \sqrt{2} = \boxed{\sqrt{2 \cdot A}}Per comprendere l’ultimo passaggio osserviamo che il prodotto tra le radici quadrate di due quantità è uguale alla radice quadrata del prodotto tra le due stesse quantità. Tale regola sarà introdotta e giustificata più avanti nel percorso degli studi.
Se invece abbiamo come dato il perimetro del quadrato, tenendo conto che {L=\dfrac{P}{4}}, basta sostituire alla lettera {L } nella prima formula l’espressione {\dfrac{P}{4}}:
d = L \cdot \sqrt{2} = \dfrac{P}{4} \cdot \sqrt{2} = \boxed{ \dfrac{P \cdot \sqrt{2}}{4}}| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
