La parabola e le equazioni di secondo grado

 - 

Equazioni (superiori)

Ci occupiamo ora di fornire un’interpretazione grafica delle soluzioni delle equazioni di secondo grado facendo uso della parabola. In particolare, mostreremo che gli eventuali punti di intersezione della parabola {y=ax^2+bx+c} con l’asse delle {x} rappresentano le soluzioni dell’equazione di secondo grado {ax^2+bx+c=0}.

Proprio grazie al collegamento tra la parabola e le equazioni di secondo grado è possibile risolvere le equazioni di secondo grado determinando i punti di intersezione tra la parabola {y=ax^2+bx+c} e l’asse delle {x}. E ricordando che l’asse delle {x} ha equazione {y=0}, si tratterà di risolvere il seguente sistema:

\begin{cases} y=ax^2+bx+c \\ \\ y= 0 \end{cases}

Ma ciò equivale semplicemente a risolvere l’equazione {ax^2+bx+c=0}.

Alla luce di queste premesse, vediamo l’interpretazione grafica delle soluzioni delle equazioni di secondo grado utilizzando la corrispondente parabola.

Parabola ed equazioni di secondo grado: discussione delle soluzioni

Il grafico della funzione:

y=ax^2+bx+c

è una parabola il cui asse di simmetria è sempre parallelo all’asse delle {y}.

La concavità della parabola sarà rivolta verso l’alto o verso il basso a seconda che il coefficiente {a} sia rispettivamente positivo o negativo.

Cerchiamo ora di capire come ci può essere di aiuto la parabola {y=ax^2+bx+c} per risolvere l’equazione {ax^2+bx+c=0}.

In particolare, riprendendo quanto già sappiamo su come risolvere le equazioni di secondo grado, distinguiamo i seguenti casi:

• se {\Delta = b^2 - 4ac } è positivo e diverso da zero, l’equazione di secondo grado {ax^2+bx+c=0} ammette due soluzioni reali e distinte {x_1} e {x_2}. Inoltre, la parabola {y=ax^2+bx+c} interseca l’asse delle {x} in due punti;
• se {\Delta = b^2-4ac } è uguale a zero, l’equazione di secondo grado {ax^2+bx+c=0} ammette due soluzioni reali e coincidenti {x_1=x_2}. Inoltre, la parabola {y=ax^2+bx+c} è tangente all’asse delle {x} nel punto {x_1 } coincidente con il punto {x_2};
• infine, se {\Delta = b^2-4ac } è minore di zero l’equazione è impossibile (ovvero non ha soluzioni) e non abbiamo punti di intersezione tra la parabola e l’asse delle {x}.

Tali situazioni sono riassunte graficamente a seguire:

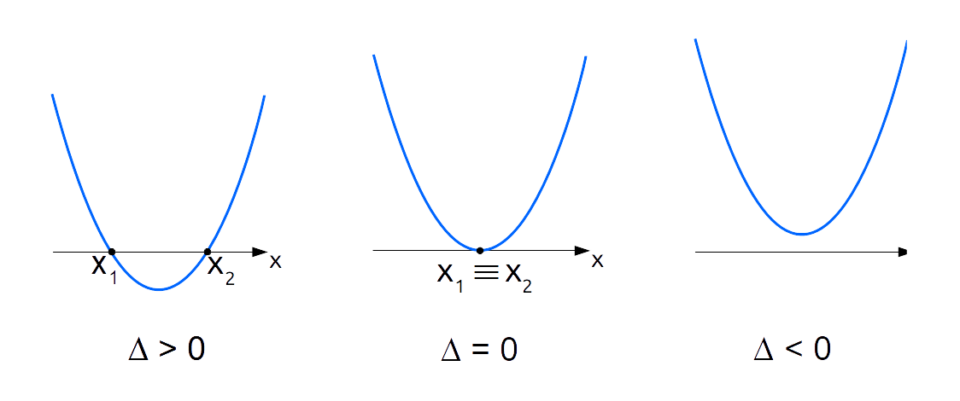
La figura si riferisce al caso in cui sia {a>0} (parabola con concavità rivolta verso l’alto). Nel caso di concavità rivolta verso il basso le considerazioni sono comunque del tutto simili.

Per quanto riguarda il legame tra la parabola e le equazioni di secondo grado è tutto. Nella prossima lezione ci occuperemo delle equazioni di secondo grado parametriche. Buon proseguimento!