In questa lezione ci occuperemo dei numeri complessi e delle operazioni che possiamo eseguire su di essi. Come vedremo, i numeri complessi risolvono il problema dei numeri reali relativo all’impossibilità di estrarre la radice quadrata di un numero negativo.
Così, grazie ai numeri complessi sarà ad esempio possibile determinare l’insieme delle soluzioni anche di equazioni di secondo grado che utilizzando i numeri reali risultano impossibili. Infatti, potendo estrarre la radice quadrata di numeri anche negativi, il fatto che il discriminante sia negativo non impedisce comunque di determinare le soluzioni dell’equazioni. Da ciò capiamo l’importanza di chiarire con quale insieme numerico lavoriamo per risolvere le equazioni di secondo grado e le equazioni algebriche in generale.
L’insieme dei numeri complessi contiene l’insieme dei numeri reali, e quindi ogni numero reale può anche essere visto come un numero complesso. Come vedremo, tuttavia, dato che l’insieme dei numeri reali è un sottoinsieme proprio dei numeri complessi, esistono anche numeri complessi che non sono numeri reali (ci riferiamo in questo caso ai numeri complessi non reali).
Nel corso della lezione vedremo la rappresentazione dei numeri complessi sia dal punto di vista algebrico, sia mediante l’utilizzo del piano cartesiano (più propriamente, del piano di Gauss, che è un piano cartesiano modificato per rappresentare i numeri complessi).
Innumerevoli sono le applicazioni dei numeri complessi, che non riguardano quindi soltanto le soluzioni complesse delle equazioni algebriche, ma che spaziano in numerosi ambiti della fisica e dell’ingegneria. Ad esempio, tali numeri hanno un’importanza fondamentale nella rappresentazione delle grandezze in corrente alternata (elettrotecnica ed elettronica).
Cominciamo allora subito lo studio dei numeri complessi e delle operazioni che possiamo eseguire su di essi. Precisiamo che la trattazione qui offerta è destinata agli studenti delle scuole superiori. Tuttavia, la lezione può essere utilizzata anche dagli universitari, che poi potranno approfondire i concetti con ulteriori risorse.
Dall’insieme dei numeri reali all’insieme dei numeri complessi
L’insieme delle soluzioni di un’equazione algebrica dipende dall’insieme numerico con il quale decidiamo di lavorare. Ad esempio, l’equazione:
x-\dfrac{1}{2}=0risulta impossibile nell’insieme dei numeri naturali o anche relativi (insiemi rispettivamente {\mathbb{N}} e {Z}). Infatti, non esiste alcun numero intero che sostituito alla {x} rende nullo il primo membro dell’equazione.
Considerando invece i numeri razionali, l’equazione diventa determinata ed ammette la soluzione {x=\dfrac{1}{2}}. Dunque, nell’insieme {Q} l’equazione non è più impossibile.
Un discorso del tutto simile può essere effettuato relativamente alle equazioni di secondo grado. Ad esempio, la seguente equazione:
x^2+5=0
non ammette alcuna soluzione reale. Infatti, non esiste alcun valore della {x} in grado di annullare il primo membro. Ciò non sorprende, poiché l’equazione può essere riscritta come:
x^2=-5
ed evidentemente il quadrato al primo membro (che è una quantità sempre positiva) non può essere uguale alla quantità negativa al secondo membro.
Tuttavia, provando a risolvere comunque l’equazione, arriviamo a scrivere:
x_{1,2}=\pm \sqrt{-5}Lavorando con i numeri reali, qui ci fermiamo poiché la radice quadrata di un numero negativo non ha significato.
Tuttavia, è possibile definire una quantità detta unità immaginaria:
i=\sqrt{-1}In tal modo otteniamo per l’equazione le soluzioni:
x_{1,2} = \pm \sqrt{-5} = \pm \sqrt{5 \cdot (-1)} = \pm \sqrt{5} \sqrt{-1} = \pm \sqrt{5}iMa tale discorso è valido soltanto lavorando con un nuovo insieme numerico, che non è più l’insieme dei numeri reali ma bensì l’insieme dei numeri complessi.
Numeri complessi: definizione
Si dice numero complesso una quantità del tipo: {a+ib, \qquad a, \: b \in \mathbb{R}}ove {i} si dice unità immaginaria e si ha in particolare {i=\sqrt{-1}}.
Così un numero complesso è la somma del numero reale {a} e del numero immaginario {ib}, detti rispettivamente parte reale e parte immaginaria del numero complesso.
In particolare, all’unità immaginaria attribuiamo le proprietà:
i=\sqrt{-1} \iff i^2=-1Tutti gli elementi del tipo {a+ib} formano l’insieme {\mathbb{C}} dei numeri complessi. E detta forma {a+ib} si dice rappresentazione algebrica dei numeri complessi.
I seguenti sono tutti esempi di numeri complessi:
3+7i, \qquad -9-5i, \qquad 4-77i
Se un numero complesso ha il coefficiente della parte immaginaria {b} uguale a zero, questo è del tipo {a+0i} ed è quindi anche un numero reale. Se invece un numero complesso ha il coefficiente della parte reale uguale a zero si dice numero immaginario (pur sempre appartenente all’insieme {\mathbb{C}}.
Nel caso in cui infine abbiamo {a \neq 0} e allo stesso tempo {b \neq 0} ci ritroviamo con dei numeri complessi non reali. In altre parole, si tratta di numeri che appartengono all’insieme {\mathbb{C}} ma non a quello dei numeri reali.
Zero ed unità dei numeri complessi
Nell’insieme {C} dei numeri complessi lo zero è dato da {0+0i}, mentre l’unità è data dal numero complesso {1+0i}.
Per convincersene, basta osservare che sommando lo zero ad un dato numero complesso otteniamo come risultato lo stesso numero complesso:
a+ib+0+0i=a+0+(b+0)i=a+ib
Infine, se moltiplichiamo un dato numero complesso per l’unità dell’insieme {\mathbb{C}}, otteniamo di nuovo il numero complesso di partenza:
(a+ib)(1+0i)=a\cdot1+a \cdot 0i+ib \cdot 1 + ib \cdot 0i=a+ib
Le due proprietà sono le stesse di quelle dello zero è dell’unità dell’insieme dei numeri reali. Infatti, detto {a} un qualsiasi numero reale si ha:
a +0=a; \qquad a \cdot 1 = a
Rappresentazione cartesiana dei numeri complessi (piano di Gauss)
Un numero complesso è quindi costituito da un numero reale (parte reale) e da un numero immaginario (parte immaginaria, ovvero un numero del tipo {bi}, con {i=\sqrt{-1}} e {b} numero reale).
Ora, possiamo convenire di rappresentare i numeri complessi in un sistema di riferimento cartesiano. In particolare, riportiamo la parte reale nell’asse delle {x} e la parte immaginaria nell’asse delle {y}. In tal modo, stabiliamo una corrispondenza biunivoca tra ciascun punto del piano cartesiano e ciascun numero complesso. Ciò è del tutto simile alla corrispondenza biunivoca a suo tempo stabilita tra ciascun numero reale e ciascun punto della retta stessa.
Il particolare piano cartesiano ove si rappresentano i numeri complessi si chiama piano di Gauss.
Così, la seguente è la rappresentazione del numero complesso {a+ib} nel piano di Gauss:
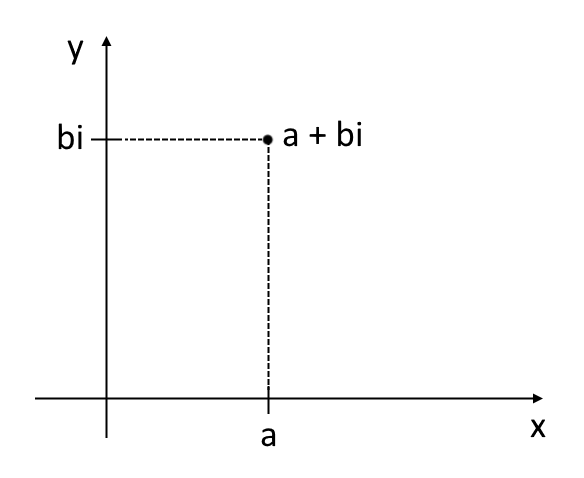
Diversamente dai numeri reali, nel caso dei numeri complessi non ha senso stabilire alcuna relazione di ordinamento. In altre parole, non ha senso chiedersi se un numero complesso è maggiore o minore dell’altro.
Infine, dato ad esempio il numero complesso {3-7i}, il suo opposto è {-3+7i}. Si tratta infatti di rileggere il numero complesso come un polinomio, e come sappiamo l’opposto di un polinomio si ottiene invertendo il segno di tutti i suoi termini.
Operazioni con i numeri complessi
Nell’insieme {\mathbb{C}} dei numeri complessi è possibile eseguire operazioni quali addizione, sottrazione e moltiplicazione, come mostreremo fra un istante. Per eseguire tali operazioni basterà considerare ciascun numero complesso come un polinomio. Infatti, se consideriamo il numero complesso:
3+5i
questo è costituito da due termini: il termine noto {3} e il termine {5i} contenente la variabile {i}. Così, nell’eseguire le operazioni tra numeri complessi l’unità immaginaria {i} deve essere vista come una variabile (o lettera).
Così, per sommare tra loro due numeri complessi, procederemo allo stesso modo della somma tra polinomi:
(3+5i)+(7-9i)=(3+7)+(5-9)i=10-4i
Effettivamente abbiamo sommato tra loro i termini simili dei polinomi.
In modo del tutto simile si procedere con la differenza:
\begin{align*} & (3+5i)-(7-9i)=3+5i+(-7+9i)=3+5i-7+9i =\\ \\ & =(3-7)+(5+9)i=-4+14i \end{align*}Osserviamo che come nel caso dei polinomi, abbiamo ricondotto la differenza tra due quantità alla somma del minuendo e dell’opposto del sottraendo.
Anche per quanto riguarda la moltiplicazione basterà procedere come nel caso della moltiplicazione tra polinomi. Ad esempio:
\small \begin{align*} & (3-9i) \cdot (-2+5i)=3 \cdot (-2)+3 \cdot 5i-9i \cdot (-2)+(-9i)\cdot5i=\\ \\ & =-6+15i+18i-45i^2=\end{align*}Ora per proseguire i passaggi dobbiamo ricordare che per la definizione di unità immaginaria si ha {i^2=-1}. Così:
=-6+15i+18i-45 (-1)=-6+33i+45=39+33i
Sulla base delle considerazioni fatte possiamo stabilire le seguenti regole.
Dati i due numeri complessi {z_1= a+ib} e {z_2=c+id} la loro somma (o differenza) è data da: {z_1 \pm z_2 = a \pm c +i(b \pm d)}
Dati i due numeri complessi {z_1 = a+ib} e {z_2=c+id} il loro prodotto è dato da: {z_1 \cdot z_2 = ac-bd+i(ad+bc)}
A voi la scelta se ragionare ogni volta come per le operazioni tra polinomi oppure ricordare le regole a memoria. 😉
Rimane da considerare l’operazione di divisione, ma prima di introdurla dobbiamo introdurre il concetto di complessi coniugati.
Complessi coniugati
Due numeri complessi del tipo {a+ib} e {a-ib} si dicono complessi coniugati.
Due numeri complessi si dicono coniugati se hanno la stessa parte reale e coefficienti della parte immaginaria opposti.
I complessi coniugati hanno la seguenti interessanti proprietà:
- due numeri complessi coniugati si rappresentano nel piano come punti simmetrici rispetto all’asse delle {x};
- il loro prodotto è un numero reale.
In merito alla seconda proprietà, osserviamo che per la regola del prodotto tra numeri complessi abbiamo:
(\underbrace{a+ib}_{A+B})(\underbrace{a-ib}_{A-B})=\underbrace{a^2-b^2\overbrace{i^2}^{-1}}_{A^2-B^2}=\boxed{a^2+b^2}Come si può vedere nel risultato non compare la parte immaginaria, e pertanto abbiamo ottenuto un numero reale.
Divisione tra numeri complessi
Vogliamo ora stabilire la regola per la divisione tra numeri dell’insieme {\mathbb{C}}. Il nostro problema è in particolare riesprimere la frazione:
\dfrac{a+ib}{c+id}nella forma {A+iB}, ovvero come un quoziente esatto dato a sua volta da un numero complesso. Ricordiamo che nella frazione il numero {a+ib} rappresenta il dividendo mentre il numero {c+id} rappresenta il divisore.
Osserviamo che la frazione è equivalente a:
\dfrac{a+ib}{c+id} \cdot \dfrac{c-id}{c-id}Stiamo in particolare moltiplicando per una frazione (equivalente ad {1}) il cui numeratore e denominatore sono dati dal coniugato del divisore.
Ora, utilizzando le regole sulle operazioni in {\mathbb{C}} sin qui stabilite abbiamo:
\begin{align*} & \dfrac{a+ib}{c+id} \cdot \dfrac{c-id}{c-id}=\dfrac{ac-adi+bci-bdi^2}{c^2-d^2i^2}= \\ \\ & =\dfrac{ac+(-ad+bc)i+bd}{c^2+d^2}= \dfrac{ac+bd+(bc-ad)i}{c^2+d^2}= \\ \\ & =\dfrac{ac+bd}{c^2+d^2}+\dfrac{bc-ad}{c^2+d^2} i\end{align*}Effettivamente abbiamo ottenuto un quoziente esatto della forma {A+iB}, con {A=\dfrac{ac+bd}{c^2+d^2}} e {B=\dfrac{bc-ad}{c^2+d^2}}. Possiamo allora stabilire la seguente regola:
La divisione tra i due numeri complessi {z_1=a+ib} e {z_2=c+id}, con {z_2 \neq 0} ha come quoziente il numero complesso: {\dfrac{z_1}{z_2}=\dfrac{ac+bd}{c^2+d^2}+\dfrac{bc-ad}{c^2+d^2}i}
Osservazione. Il metodo utilizzato per arrivare al quoziente della divisione tra numeri complessi ricorda indubbiamente la razionalizzazione di frazioni con denominatore del tipo {a+\sqrt{b}}. Infatti, nel caso della divisione tra numeri complessi l’obiettivo è quello di rendere reale il denominatore della frazione che rappresenta la divisione, allo stesso modo in cui nella razionalizzazione di una frazione l’obiettivo è quello di rendere razionale il denominatore.
Consideriamo ad esempio la divisione:
\dfrac{5+3i}{5-3i}Possiamo procedere ragionando con il coniugato del divisore oppure ricordando la regola diretta. Nel primo caso, osservando che il coniugato del divisore {5-3i} è {5+3i}, abbiamo:
\begin{align*} & \dfrac{5+3i}{5-3i}=\dfrac{5+3i}{5-3i} \cdot \dfrac{5+3i}{5+3i}=\dfrac{(5+3i)^2}{25-(3i)^2}=\dfrac{25+30i+(3i)^2}{25-3^2i^2}=\\ \\ & =\dfrac{25+30i+3^2i^2}{25-9i^2}=\dfrac{25+30i-9}{25+9}=\dfrac{16+30i}{34}=\\ \\ & =\dfrac{8}{17}+\dfrac{15}{17}i \end{align*}Osserviamo che abbiamo utilizzato la proprietà {i^2=-1}.
Ragionando invece con la regola diretta:
\begin{align*} & \dfrac{5+3i}{5-3i}=\dfrac{a+ib}{c+id}=\dfrac{ac+bd}{c^2+d^2}+\dfrac{bc-ad}{c^2+d^2}i= \\ \\ & =\dfrac{5\cdot5+3\cdot(-3)}{5^2+(-3)^2}+\dfrac{3\cdot5-5\cdot(-3)}{5^2+(-3)^2}= \\ \\ & = \dfrac{25-9}{25+9} + \dfrac{15+15}{25+9}i=\dfrac{16}{34}+\dfrac{30}{34}i=\\ \\ & =\dfrac{8}{17}+\dfrac{15}{17}i\end{align*}Noi di SìMatematica troviamo più pratico ragionare con il coniugato del divisore, ma a voi la scelta di quale metodo utilizzare.
Rappresentazione delle operazioni di addizione e sottrazione nel piano di Gauss
Concludiamo la lezione mostrando la rappresentazione sul piano di Gauss dell’addizione e sottrazione tra numeri complessi.
Cominciamo partendo dalla somma:
z_1 + z_2
con {z_1=a+ib} e {z_2 = c+id}. Rappresentiamo anzitutto ciascun numero complesso nel piano di Gauss come un segmento orientato che unisce l’origine degli assi con il punto del piano di Gauss che corrisponde al numero complesso considerato:
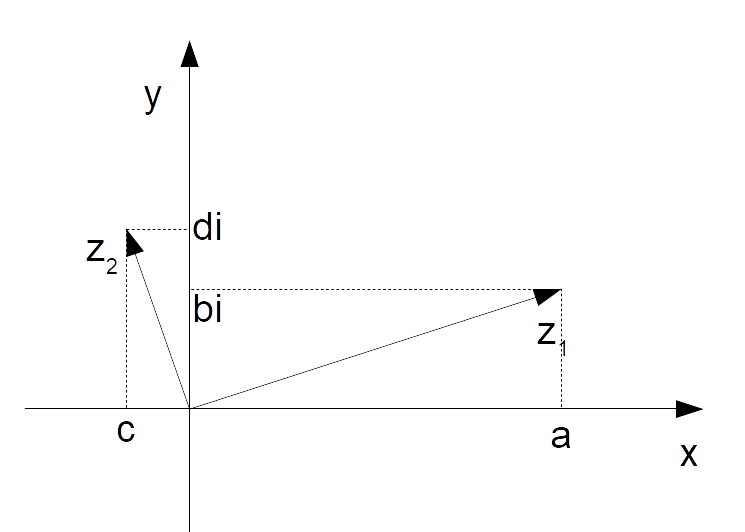
Ora non resta che costruire un parallelogramma avente per lati i segmenti che uniscono l’origine con i punti che rappresentano gli addendi. La diagonale del parallelogramma punterà al risultato della somma:
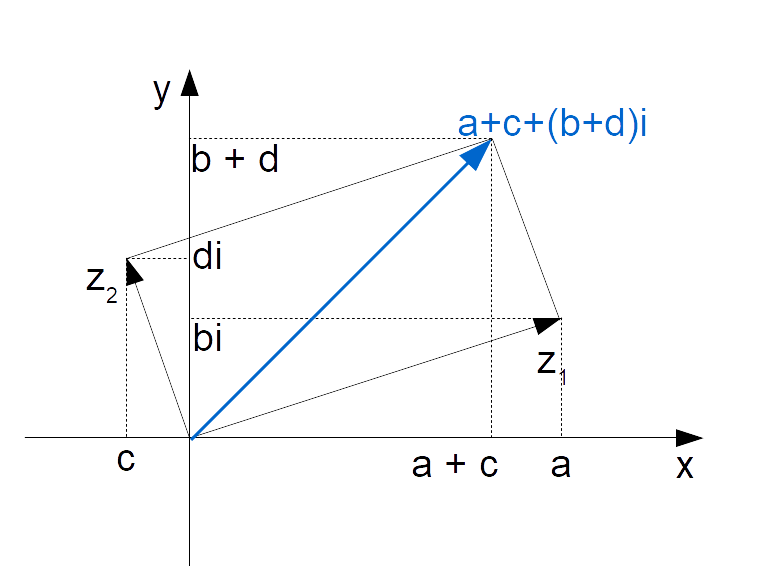
Per quanto riguarda invece la differenza tra numeri complessi, procederemo in modo del tutto simile alla somma, rappresentando tuttavia l’opposto del sottraendo. In tal modo riconduciamo la differenza alla somma del minuendo e dell’opposto del sottraendo.
Così dovremo ricondurre la differenza {z_1-z_2} alla somma {z_1+(-z_2)} ed abbiamo:
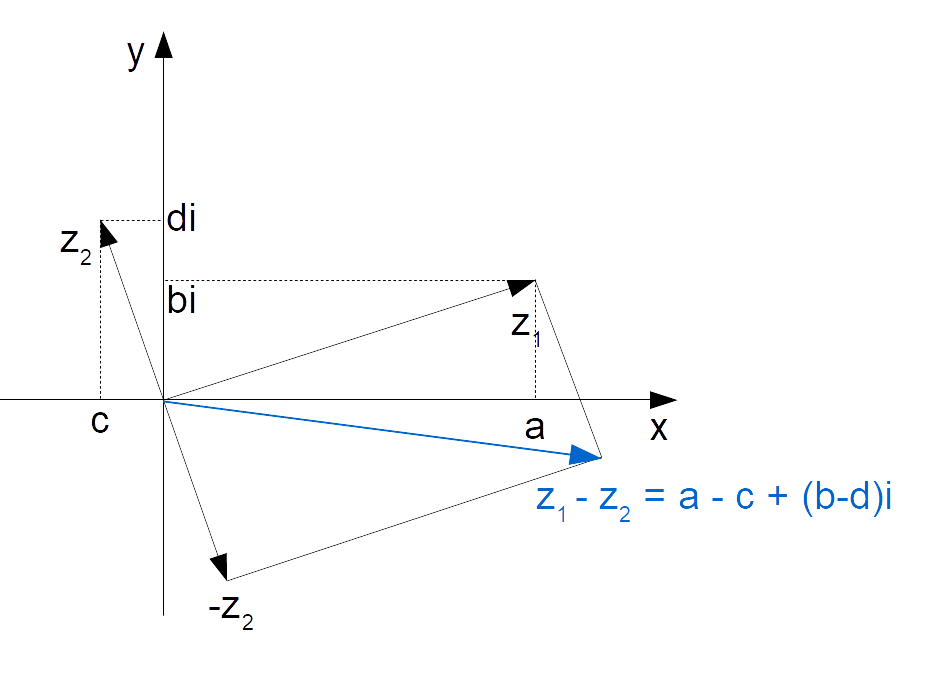
Conclusioni
Per quanto riguarda questa lezione sulla definizione di numero complesso è tutto. Abbiamo qui fornito le nozioni per gli studenti delle scuole superiore, che costituiscono comunque un’utile infarinatura anche per gli studenti universitari.
Nella prossima lezione vedremo come risolvere le equazioni di secondo grado lavorando nell’insieme {\mathbb{C}} e non solo in {\mathbb{R}}. Buon proseguimento!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
