Somma vettoriale

 - 

Domande e risposte

Cosa si intende per somma vettoriale e come si calcola?

Per avere una buona panoramica relativamente alla somma vettoriale (o somma tra vettori) svilupperemo i seguenti punti:

• somma di vettori algebrici;
• calcolo del modulo del vettore risultato della somma tra vettori;
• infine, somma di vettori geometrici, con il metodo punta-coda e con la regola del parallelogramma.

Definizione di somma vettoriale

Consideriamo in via generale due vettori {\textbf{v}} e {\textbf{w}}. La loro somma vettoriale è ancora un vettore e si indica con:

\textbf{v}+\textbf{w}

Se sono note le componenti cartesiane dei vettori {\textbf{v}} e {\textbf{w}} lungo ciascun asse, la loro somma è un vettore tale che ciascuna sua componente cartesiana è data dalla somma delle componenti cartesiane lungo lo stesso asse di ciascuno dei vettori di partenza.

Diversamente, per via geometrica è possibile eseguire la somma tra vettori o mediante il metodo punta-coda, o utilizzando la regola del parallelogramma.

Somma algebrica tra vettori

Supponiamo di avere due vettori di {\R^2}:

\textbf{v}=\left \langle {v_x, v_y} \right \rangle, \qquad \textbf{w}=\left \langle {w_x, w_y} \right \rangle

Nota. Nella rappresentazione dei vettori, in alternativa alle parentesi angolate è possibile utilizzare le parentesi tonde.

La loro somma , calcolata per via algebrica, è data dal vettore:

\textbf{v}+\textbf{w}=\left \langle {v_x+w_x, v_y+w_y} \right \rangle

Osserviamo che nel vettore risultato della somma, ciascuna componente (cartesiana) lungo un dato asse è data dalla somma delle rispettive componenti (cartesiane) di ciascun vettore di partenza lungo quello stesso asse.

Nel caso dei vettori di {\R^3}, ovvero:

\textbf{v}=\left \langle {v_x, v_y,v_z} \right \rangle, \qquad \textbf{w}=\left \langle {w_x, w_y, w_z} \right \rangle

abbiamo, in modo del tutto simile:

\textbf{v}+\textbf{w}=\left \langle {v_x+w_x,v_y+w_y,v_z+w_z} \right \rangle

In generale, se consideriamo due vettori di uno spazio n-dimensionale, ossia:

\textbf{v}=\left \langle {v_1, v_2, \dots v_n} \right \rangle, \qquad \textbf{w}=\left \langle {w_1,w_2,\dots, w_n} \right \rangle, \qquad n \in \N

allora per la somma tra i vettori con il metodo algebrico abbiamo:

\textbf{v}+\textbf{w}=\left \langle {v_1+w_1, v_2+w_2, \dots, v_n+w_n} \right \rangle

Esempio (somma algebrica tra vettori)

Sommare tra loro i vettori di {\R^2} {\textbf{v}=\left \langle {5,7} \right \rangle} e {\textbf{w}=\left \langle {-2,-3} \right \rangle}.

Anzitutto, per quanto riguarda le componenti cartesiane dei vettori abbiamo:

\begin{align*} & \textbf{v}=\left \langle {5,7} \right \rangle=\left \langle {v_x, v_y} \right \rangle \quad \Rightarrow \quad v_x=5, \: v_y=7 \\ \\ & \textbf{w}=\left \langle {-2, -3} \right \rangle=\left \langle {w_x, w_y} \right \rangle \quad \Rightarrow \quad w_x=-2, \: w_y=-3 \end{align*}

Così per la somma dei vettori dati possiamo scrivere:

\textbf{v}+\textbf{w}=\left \langle {v_x+w_x, v_y+w_y} \right \rangle=\left \langle {5+(-2), 7+(-3)} \right \rangle=\left \langle {3,4} \right \rangle

Modulo del risultato della somma vettoriale

Il modulo o norma del vettore risultato della somma vettoriale è esprimibile in funzione delle coordinate cartesiane dei vettori {\textbf{v}} e {\textbf{w}} di partenza come:

\small\begin{align*} &\lVert {\textbf{v}+\textbf{w}} \rVert = \sqrt{(v_x+w_x)^2+(v_y+w_y)^2} ,\qquad (\text{in} \: \R^2); \\ \\ & \lVert {\textbf{v}+\textbf{w}} \rVert=\sqrt{(v_x+w_x)^2+(v_y+w_y)^2+(v_z+w_z)^2}, \qquad (\text{in} \: \R^3); \\ \\ &\lVert {\textbf{v}+\textbf{w}} \rVert = \sqrt{(v_1+w_1)^2+(v_2+w_2)^2+\dots +(v_n+w_n)^2}, \qquad (\text{in} \: \R^n)\end{align*}

Se invece disponiamo come dati di partenza dei moduli dei vettori {\textbf{v}}, {\textbf{w}} e dell’angolo {\theta} tra essi compreso, il modulo della somma vettoriale si calcola come:

\lVert {\textbf{v}+\textbf{w}} \rVert = \sqrt{\lVert {\textbf{v}} \rVert^2+\lVert {\textbf{w}} \rVert^2+2 \cdot \lVert {\textbf{v}} \rVert \cdot \lVert {\textbf{w}} \rVert \cdot \cos (\theta)}

Tale formula è conseguenza del teorema del coseno (o teorema di Carnot).

Esempio (modulo del vettore somma vettoriale con le componenti cartesiane)

Con riferimento all’esempio precedente, il modulo della somma vettoriale {\textbf{v}+\textbf{w}} è dato da:

\begin{align*} & \lVert {\textbf{v}+\textbf{w}} \rVert=\sqrt{(v_x+w_x)^2+(v_y+w_y)^2}=\\ \\ & =\sqrt{[5+(-2)
]^2+[7+(-3)]^2}=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5 \end{align*}

In alternativa, ricordando che il modulo di un vettore {\textbf{v}} è dato da:

\lVert {\textbf{v}} \rVert=\sqrt{v_x^2+v_y^2}

essendo nell’esempio precedente {\textbf{v}+\textbf{w}=\left \langle {3,4} \right \rangle}, si ha:

\lVert {\textbf{v}+\textbf{w}} \rVert=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5

Per cui volendo calcolare il modulo della somma vettoriale, è possibile anzitutto calcolare le componenti cartesiane del vettore somma, quindi calcolare il modulo del vettore somma stesso a partire da esse.

Esempio (modulo del vettore somma vettoriale con i moduli dei vettori di partenza e con l’angolo tra essi compreso)

Calcolare il modulo del vettore somma vettoriale dei vettori {\textbf{v}} e {\textbf{w}}, con {\lVert {\textbf{v}} \rVert = \sqrt{74}}, {\lVert {\textbf{w}} \rVert = \sqrt{13}} e angolo compreso tra i due vettori {\theta = 178,152^\circ}

Abbiamo:

\begin{align*} & \lVert {\textbf{v}+\textbf{w}} \rVert=\sqrt{\lVert {\textbf{v}} \rVert^2+\lVert {\textbf{w}} \rVert^2+ 2 \cdot \lVert {\textbf{v}} \rVert \cdot \lVert {\textbf{w}} \rVert \cdot \cos (\theta)}=\\ \\ & =\sqrt{\left( \sqrt{74}\right)^2 + \left( \sqrt{13}\right)^2+ 2 \cdot \sqrt{74}\cdot\sqrt{13} \cdot \cos (178,152^\circ)}=\\ \\ & =\sqrt{74+13-62}=\sqrt{25}=5\end{align*}

Come sommare due vettori tra loro con un metodo geometrico

Esistono due modi per poter sommare due vettori tra loro (somma vettoriale) utilizzando delle costruzioni geometriche:

• regola del parallelogramma;
• metodo punta-coda.

Regola del parallelogramma

Mediante una traslazione (e quindi tramite un movimento rigido) facciamo coincidere i punti di applicazione (o origini) dei due vettori {\textbf{v}} e {\textbf{w}} da sommare. Successivamente, costruiamo un parallelogramma i cui lati condividono le stesse misure dei segmenti orientati che rappresentano i vettori.

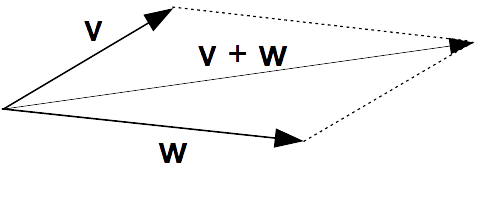
Alla diagonale del parallelogramma corrisponde il vettore {\textbf{v}+\textbf{w}}, ovvero la somma vettoriale tra i due vettori {\textbf{v}} e {\textbf{w}}.

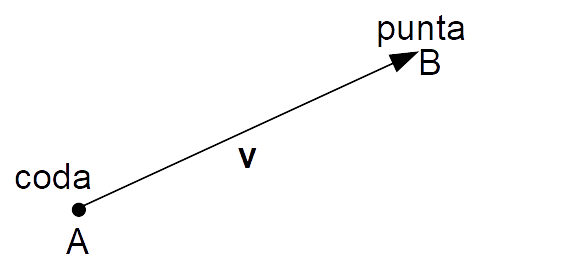
Metodo punta-coda

Ricordiamo che la coda di un vettore è il suo punto di applicazione, mentre la punta è il punto corrispondente alla freccia del vettore.

Ciò premesso, se dobbiamo sommare tra loro due vettori {\textbf{v}} e {\textbf{w}}, con il metodo punta-coda l’idea è quella di far coincidere, mediante un movimento rigido, la punta del vettore {\textbf{v}} con la coda del vettore {\textbf{w}}. In tal modo, il vettore avente per coda la coda del vettore {\textbf{v}} e per punta la punta del vettore {\textbf{w}} rappresenta la somma vettoriale tra i due vettori dati.

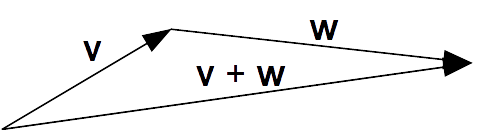
Proprietà della somma vettoriale

Dati tre vettori {\textbf{u}}, {\textbf{v}} e {\textbf{w}} appartenenti ad un dato spazio vettoriale {V}, valgono le seguenti proprietà:

• proprietà commutativa: {\textbf{u}+\textbf{v}= \textbf{v} + \textbf{u}};
• proprietà associativa: {\textbf{u}+(\textbf{v}+\textbf{w})=(\textbf{u}+\textbf{v})+\textbf{w}};
• esistenza dell’elemento neutro. Esiste un particolare vettore, indicato con {\textbf{0}} e detto vettore nullo, tale da essere l’elemento neutro della somma vettoriale, ovvero tale da far valere la proprietà, per ogni vettore {\textbf{v}} dello spazio vettoriale {V}: {\textbf{v}+\textbf{0}=\textbf{0}+\textbf{v}=\textbf{v}};
• esistenza dell’elemento opposto: per ogni vettore {\textbf{v}} dello spazio vettoriale {V} esiste ed è unico il vettore {-\textbf{v}} detto vettore opposto di {\textbf{v}} tale da rispettare la proprietà: {\textbf{v}+(-\textbf{v})=\textbf{0}}.

Per ulteriori informazioni sulla somma tra vettori e sui vettori in generale rimandiamo alle lezioni sui vettori del sito Altramatica.