Teorema del resto e teorema di Ruffini

 - 

Monomi e polinomi (superiori)

Vediamo in questa lezione il teorema del resto e il teorema di Ruffini, due importanti teoremi che riguardano la divisione tra polinomi, nel particolare caso in cui il polinomio divisore sia un binomio della forma {x-c}, con {c \in \mathbb{R}}.

Nel caso in cui il polinomio divisore sia quindi un binomio di primo grado nella particolare forma indicata, il teorema del resto e il teorema di Ruffini ci consentono di ricavare importanti informazioni senza eseguire la divisione tra polinomi. In altre parole, grazie a detti teoremi non dovremo eseguire la divisione tra polinomi secondo la procedura vista nella precedente lezione. Lo ribadiamo, questo però soltanto nel caso in cui il divisore sia della forma {x-c}.

Nello specifico, il teorema del resto fornisce una valutazione del resto della divisione senza dover eseguirla. Invece, il teorema di Ruffini ci permette di capire sotto opportune condizioni se due polinomi sono divisibili o meno. E anche in questo caso, senza dover eseguire la divisione.

Vediamo allora subito il teorema del resto e il teorema di Ruffini.

Teorema del resto

Vediamo subito l’enunciato del teorema del resto.

Il resto della divisione tra un polinomio {P(x)} e un polinomio della forma {x-c, \: c \in \mathbb{R}} è dato dalla valutazione di {P(x)} nel punto {c}. {P(x):(x-c) \quad \Rightarrow \quad R(x)=P(c)}

Così ad esempio, consideriamo la divisione:

(x^3-2x^2+5x):(x-2)

con polinomio dividendo {P(x)=x^3-2x^2+5x} e polinomio divisore {x-2}. Poiché il divisore è della forma richiesta dal teorema del resto, ovvero {x-c} con {c=2}, concludiamo direttamente che il resto della divisione è dato da:

R(x)=P(2)=2^3-2\cdot 2^2 + 5 \cdot 2 = 8-8+10 = 10

In pratica abbiamo sostituito nel dividendo {P(x)=x^3-2x^2+5x} il valore {x=c}, ovvero {x=2}.

Così, il teorema del resto ci permette di determinare il resto della divisione senza dover eseguire la divisione stessa. Per prova, possiamo eseguire la divisione normalmente e controllare se effettivamente otteniamo resto {R(x)=10}.

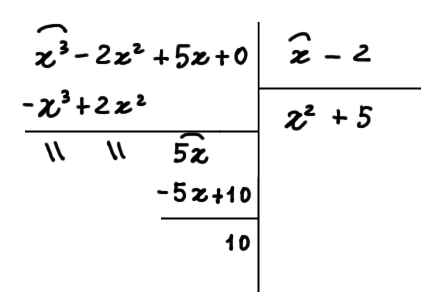
Effettivamente otteniamo {R(x)=10}. Ecco dunque l’utilità del teorema del resto.

Dimostrazione del teorema del resto

Vediamo ora come dimostrare il teorema del resto.

Ricordiamo che il grado del quoziente della divisione tra polinomi è uguale alla differenza tra il grado del dividendo e il grado del divisore. Così, se il grado di {P(x)} è {n}, possiamo sicuramente affermare che il grado del quoziente che si ottiene dalla divisione {P(x):(x-c)} è {n-1}. Infatti il divisore {x-c} è di primo grado. Inoltre, per quanto sappiamo sulla divisione tra polinomi il resto ha sicuramente grado minore di {1} (grado minore rispetto a quello del divisore). Di conseguenza, il resto dovrà essere un numero.

Ora, se {Q(x)} è il quoziente della divisione {P(x):(x-c)} e {R(x)} è il suo resto, posto che il divisore è {D(x)=x-c} dovrà essere:

P(x)=Q(x)\cdot D(x)+R(x)  = Q(x) (x-c)+R(x)

Osserviamo che il resto essendo nel nostro caso un numero non dipende da {x} e possiamo quindi indicarlo semplicemente con {R}. Per cui la precedente diviene:

P(x)=Q(x)(x-c)+R

Ora, come è chiaro dall’uguaglianza l’espressione a secondo membro è semplicemente un altro modo per riesprimere il polinomio {P(x)}. Quindi, sostituendo alle {x} al secondo membro il valore {c}, otteniamo necessariamente la valutazione {P(c)}. Così:

P(c)=\underbrace{Q(c)(c-c)}_{0}+R \quad \Rightarrow \quad P(c)=R

Quindi la valutazione di {P(x)} in {c} fornisce il resto della divisione {P(x):(x-c}), come volevamo dimostrare.

Teorema di Ruffini

Veniamo ora all’enunciato del teorema di Ruffini.

Il polinomio {P(x)} è divisibile per il binomio {x-c} se e solo se la valutazione del polinomio {P(x)} in corrispondenza di {c} è zero, ovvero {P(c)=0}.

Dimostrazione del teorema di Ruffini

Il teorema è diretta conseguenza del concetto di divisibilità tra polinomi e del teorema del resto. Infatti, sappiamo che se il polinomio {P(x)} è divisibile per il polinomio {D(x)}, il resto della divisione {P(x):D(x)} è zero. Inoltre, il teorema del resto afferma che il resto della divisione {P(x):(x-c)} è dato dalla valutazione {P(c)}. Per cui in conclusione se {P(x)} è divisibile per {x-c} dovrà essere necessariamente {P(c)=0}. E ciò dimostra il teorema di Ruffini.

Riflettiamo ora su un’importante conseguenza del teorema di Ruffini, che si sarà utile per il futuro. In particolare, se dato un polinomio {P(x)} vediamo che questo si annulla per un certo valore {c} della {x}, allora in forza del teorema di Ruffini possiamo affermare che il polinomio è divisibile per il binomio {x-c}. Teniamo bene a mente questo risultato perché ci sarà utile tra qualche lezione per poter scomporre i polinomi con la regola di Ruffini.

Esempi sul teorema del resto e sul teorema di Ruffini

Vediamo ora degli esercizi di esempio sul teorema del resto e sul teorema di Ruffini. Mostreremo i casi nei quali è possibile applicare i teoremi e le considerazioni che ci permetteranno di fare.

Esempi sul teorema del resto

Esempio 1

Calcolare il resto della divisione:

(x^2+3x+7):(x-4)

Poiché il polinomio divisore {x-c} è in questo caso {x-4} abbiamo {c=4}. Sostituiamo allora il valore {4} alla {x} nel polinomio dividendo {P(x) = x^2+3x+7}:

P(c)=P(4)=4^2+3 \cdot 4 + 7 = 16+12+7 = 35

Concludiamo allora che il resto della divisione data è {R=35}.

Esempio 2

Calcolare il resto della divisione:

(x^3+2x^2-7x+5):(x+3)

Attenzione. Poiché nel polinomio divisore il segno che separa i termini è il più, dobbiamo considerare {c=-3} e non {c=3}. Infatti, a partire dal polinomio divisore nella forma generica {x-c}, sostituendo {c=-3} otteniamo correttamente l’espressione del polinomio divisore {x-(-3)}, e quindi {x+3}. In caso di dubbio nello stabilire il valore di {c} è dunque importante sostituirlo nell’espressione {x-c} e verificare se otteniamo il polinomio divisore.

Sostituendo quindi alla {x} il valore {-3} nel polinomio dividendo otteniamo:

P(-3)=(-3)^3+2(-3)^2-7(-3)+5 = -27+18+21+5=17

Per cui in conclusione il resto della divisione è {R=17}.

Esempio 3

Calcolare il resto della divisione:

\left(2x^2+\dfrac{1}{3}x-1\right) :\left(2x+3\right)

Attenzione. Il polinomio divisore {2x+3} non è nella forma {x-c}. Infatti, il coefficiente del termine in {x} è diverso da {1}. Prima di procedere dobbiamo allora riscrivere la divisione di modo che il divisore sia della forma {x-c}. Ciò ci permetterà di applicare il teorema del resto.

In particolare dobbiamo utilizzare la proprietà invariantiva della divisione. Si tratta cioè di dividere entrambi il dividendo e il divisore per il coefficiente che accompagna la {x} nel polinomio divisore (in questo caso, {2}). Così abbiamo: {\begin{align*} &\left(2x^2+\dfrac{1}{3}x-1\right) :\left(2x+3\right)=\left[\left(2x^2+\dfrac{1}{3}x-1\right):2 \right]:\left[\left(2x+3\right):2\right]= \\ \\ & =(x^2+\dfrac{1}{6}x-\dfrac{1}{2}):\left(x+\dfrac{3}{2}\right)\end{align*}}E’ fondamentale osservare che la divisione così riscritta ha sì lo stesso quoziente della divisione di partenza, ma il resto risulterà anch’esso diviso per il coefficiente del termine in {x} del divisore di partenza. Una volta calcolato il resto dovremo quindi moltiplicarlo per il coefficiente stesso. In tal modo otterremo correttamente il resto della divisione iniziale.

Cominciamo allora riscrivendo la divisione di partenza come:

\left(x^2+\dfrac{1}{6}x-\dfrac{1}{2}\right):\left(x+\dfrac{3}{2}\right)

A questo punto possiamo utilizzare il teorema del resto relativamente ai polinomi {P(x) =x^2+\dfrac{1}{6}x-\dfrac{1}{2} } e {D(x)=x+\dfrac{3}{2}}. Osserviamo che nel polinomio divisore il segno che separa i termini è il più. Di conseguenza, dobbiamo prendere {c=-\dfrac{3}{2}}. Abbiamo:

\small P(c)=P\left(-\dfrac{3}{2}\right)=\left( -\dfrac{3}{2}\right)^2+\dfrac{1}{6} \cdot \left( -\dfrac{3}{2}\right)-\dfrac{1}{2}=\dfrac{9}{4}-\dfrac{1}{4}-\dfrac{1}{2}=\dfrac{3}{2}=R'

Ora, attenzione. Il resto {R'=\dfrac{3}{2}} non si riferisce alla divisione di partenza. Dobbiamo infatti moltiplicare il resto ottenuto per {2}, ovvero per il coefficiente che accompagna il termine in {x} nel divisore di partenza (il divisore di partenza è {\boxed{2}x+3}). Abbiamo:

R=R' \cdot 2 = \dfrac{3}{2} \cdot 2 = 3 

e questo finalmente è il resto cercato.

Esempio sul teorema di Ruffini

Stabilire se il polinomio {x^2+2x-3} è divisibile per il polinomio {x-1}.

Poiché il polinomio divisore è nella forma {x-c}, con {c=1}, si tratterà di controllare se la valutazione {P(c)} relativa al polinomio dividendo è uguale a zero. Se tale condizione risulterà verificata per il teorema di Ruffini potremo concludere che il polinomio {P(x)=x^2+2x-3} è divisibile per {x-1}. Abbiamo:

P(1)=1^2+2 \cdot 1 -3 = 3-3=0

Quindi il polinomio {x^2+2x-3} è divisibile per il polinomio {x-1}.

Per quanto riguarda il teorema del resto e il teorema di Ruffini è tutto. Nella prossima lezione ci occuperemo della regola di Ruffini per la divisione tra polinomi. Buon proseguimento!