Dopo aver visto il teorema di Ruffini e il teorema del resto, in questa lezione ci occuperemo di come eseguire la divisione tra polinomi con la regola di Ruffini.
La divisione con la regola di Ruffini è un procedimento che consente di eseguire la divisione tra polinomi in modo rapido. La condizione è che il polinomio divisore sia di primo grado e della forma {x-c}, con {c \in \mathbb{R}}.
Nella precedente lezione, utilizzando il teorema del resto ci è stato possibile determinare immediatamente il resto della divisione di un polinomio {P(x)} per un monomio {x-c}. Ora, con la regola di Ruffini potremo determinare entrambi il quoziente e il resto della divisione {P(x):(x-c)} utilizzando una procedura semplificata.
Vediamo allora la regola di Ruffini per la divisione tra polinomi.
Regola di Ruffini per la divisione tra polinomi
Supponiamo di dover eseguire una divisione tra polinomi del tipo:
P(x):(x-c), \qquad c \in \mathbb{R}ove il polinomio dividendo {P(x)} è un generico polinomio mentre il polinomio divisore è esclusivamente della forma {x-c}, ove {c} è un certo numero reale.
La regola di Ruffini si propone come alternativa alla divisione tra polinomi con il metodo generale esclusivamente per il caso di un divisore del tipo {x-c}.
Supponiamo di dover eseguire la divisione:
(x^2-7x+8):(x-6)
Il polinomio dividendo è {x^2-7x+8} mentre il polinomio divisore è {x-6}.
Come per la divisione tra polinomi secondo la regola generale, il primo passo consiste nell’ordinare per potenze decrescenti della {x} entrambi i polinomi dividendo e divisore. Inoltre, dovremo riscrivere se necessario il polinomio dividendo in forma completa, ovvero indicando esplicitamente dei coefficienti zero per le potenze della {x} mancanti. In questo caso, tuttavia, entrambi i polinomi sono ordinati e il polinomio dividendo è completo (infatti la {x} compare nel polinomio con tutte le potenze comprese tra {2} e 0).
La regola consiste nel costruire una tabella come la seguente, nella quale riportiamo i coefficienti del polinomio dividendo. Scriviamo i coefficienti di modo che la linea verticale a destra separi tra loro gli ultimi due coefficienti.
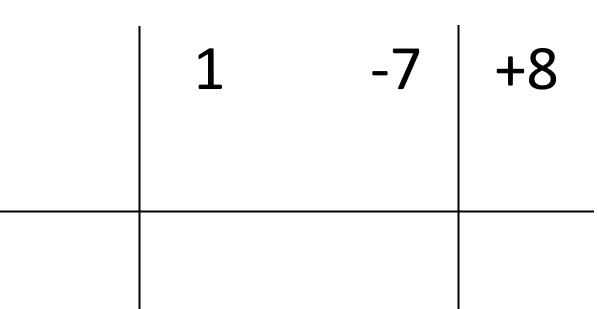
Ora, il polinomio divisore è {x-6}. Consideriamo la sua forma generale, ovvero {x-c}. Nel nostro caso abbiamo {c=6}. Scriviamo questo valore nella parte sinistra della tabella, sopra la riga orizzontale, come segue:
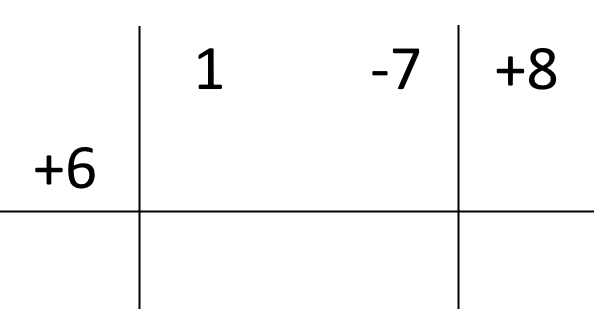
Ora, nella riga del quoziente (la parte della tabella al di sotto della riga orizzontale) riportiamo il primo coefficiente del polinomio dividendo, come segue:
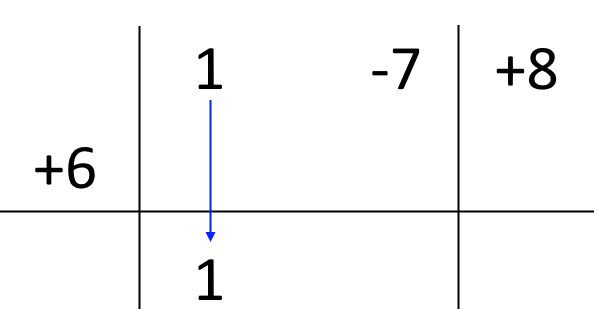
A questo punto moltiplichiamo tra loro il valore di {c} (ovvero il numero {6}) per l’ultimo numero scritto (che rappresenta il primo coefficiente del quoziente della divisione). Scriviamo il risultato sotto il secondo coefficiente del polinomio dividendo:
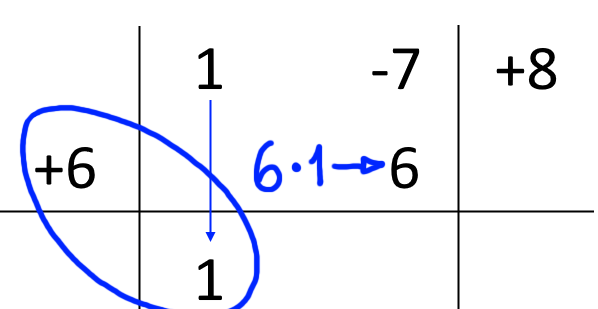
Ora sommiamo algebricamente tra di loro l’ultimo numero scritto e il numero sopra di esso (ovvero, il secondo coefficiente del polinomio dividendo).
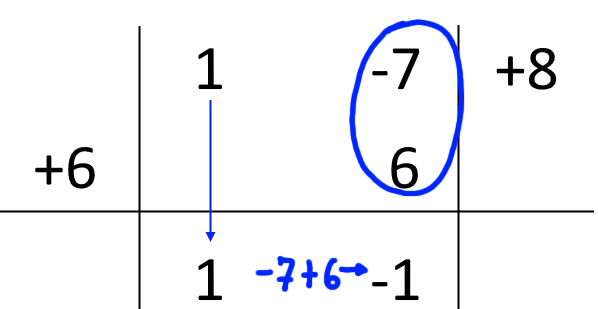
A questo punto riprendiamo il valore di {c} (ovvero il numero {6} a sinistra) e moltiplichiamolo per l’ultimo numero scritto:
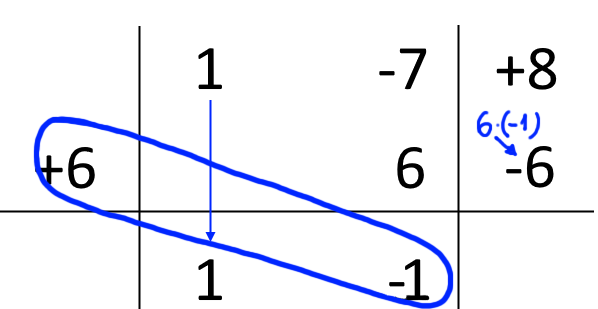
Infine, sommiamo algebricamente tra loro l’ultimo numero scritto e il numero sopra di esso:
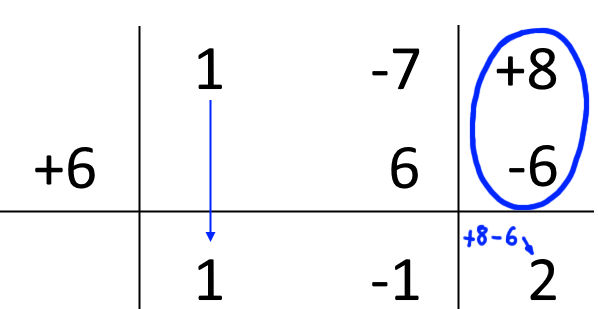
Siamo arrivati. I numeri nell’ultima riga in basso compresi tra le due linee verticali, e quindi {1} e {-1}, rappresentano i coefficienti del quoziente della divisione tra i due polinomi di partenza. L’ultimo numero a destra in basso rappresenta invece il resto della divisione stessa.
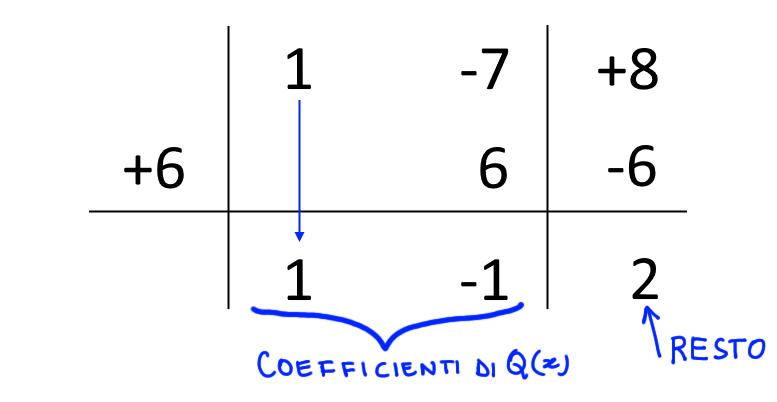
Ora, poiché il polinomio dividendo ha grado {2} e il polinomio divisore ha grado {1}, il quoziente avrà grado {2-1=1} (vedi grado del polinomio quoziente). Di conseguenza, i coefficienti di {Q(x)} sono ordinatamente i coefficienti del termine in {x} e del termine di grado zero del quoziente. Così abbiamo in conclusione:
Q(x) = x-1, \qquad R = 2
E questi sono il quoziente e il resto della divisione di partenza.
Eseguendo la divisione secondo la regola generale troviamo conferma dei risultati appena ottenuti:
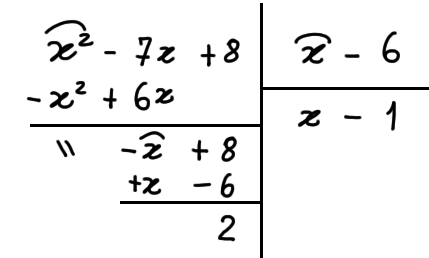
Divisione con la regola di Ruffini: un ulteriore esempio
Vediamo ora una divisione con polinomio dividendo di terzo grado. La regola da seguire è comunque la stessa. Calcoliamo quoziente e resto della divisione mediante la regola di Ruffini:
(2x^2+4x^3-5):(x+3)
Osserviamo anzitutto che il polinomio dividendo non è ordinato. Inoltre, non è nemmeno completo. Dobbiamo dunque riscrivere opportunamente il polinomio dividendo, come segue:
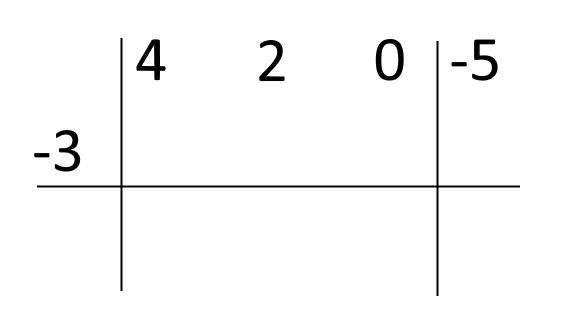
(4x^3+2x^2+0x-5):(x+3)
Il polinomio dividendo è della forma {x-c}, con {c=-3} (attenzione al segno). Scriviamo i coefficienti del polinomio dividendo e il valore della lettera {c} nella tabella:
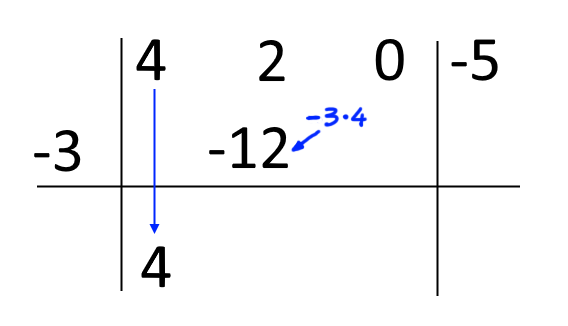
Ora riportiamo il primo coefficiente del polinomio dividendo al di sotto della riga orizzontale. Moltiplichiamo inoltre tale valore per {c=-3}, e scriviamo il risultato sotto il secondo coefficiente del polinomio dividendo:
Ora sommiamo algebricamente l’ultimo numero scritto con il numero sopra di esso. Scriviamo il risultato immediatamente sotto. Quindi, moltiplichiamo il risultato ottenuto per {c=-3} e scriviamo il risultato corrispondente nel primo posto libero al di sopra della riga orizzontale:
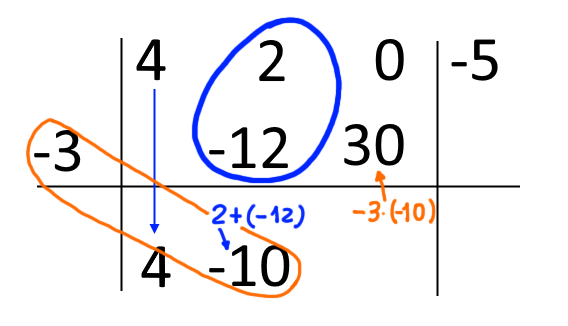
Concludiamo sommando algebricamente l’ultimo numero scritto con il numero sopra di esso. Quindi moltiplichiamo {c=-3} per il risultato della somma, scrivendo quest’ultimo risultato al di sotto dell’ultimo coefficiente del polinomio dividendo. Infine, sommiamo algebricamente l’ultimo numero scritto con il numero al di sopra di esso, e scriviamo il risultato della somma nell’ultimo posto rimasto nella tabella.
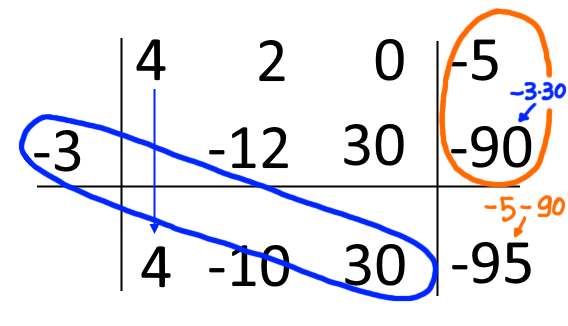
Siamo arrivati. I coefficienti del polinomio quoziente sono {4, \: -10, \: 30}. Il resto della divisione è uguale a {-95}.
Poiché il polinomio dividendo è di terzo grado, e il divisore come d’obbligo per la regola di Ruffini è di primo grado, il polinomio quoziente è di secondo grado. Quindi i coefficienti scritti sono ordinatamente il coefficiente del termine in {x^2}, del termine in {x} e del termine noto del polinomio quoziente. Di conseguenza possiamo in conclusione scrivere per la divisione di partenza:
Q(x)=4x^2-10x+30, \qquad R=-95
Conclusioni
Per quanto riguarda la divisione con la regola di Ruffini dei polinomi è tutto. E’ importante tenere bene a mente questa regola per due motivi. Anzitutto, essa permette di eseguire la divisione tra due polinomi molto rapidamente. Ovviamente, lo ricordiamo, a patto che il polinomio divisore sia della forma {x-c}. Ora, come abbiamo visto per il teorema del resto, la regola può essere applicata anche ad un divisore che non sia propriamente della forma {x-c} ma che sia comunque di primo grado. Ad esempio, nella divisione:
(4x^4-31x^2-2):(2x+1)
il divisore non è della forma {x-c} poiché il coefficiente della {x} è diverso da {1}. Come abbiamo visto per il teorema del resto, dobbiamo applicare la proprietà invariantiva della divisione. Dovremo quindi dividere per {2} sia il dividendo, sia il divisore:
[(4x^4-31x^2-2):2]:[(2x+1):2] = \left(2x^4-\dfrac{31}{2}x^2-1\right):\left(x+\dfrac{1}{2}\right)A questo punto si tratterà di eseguire la divisione con la regola di Ruffini, come visto in questa lezione. Il quoziente che otterremo sarà già il quoziente della divisione di partenza. Invece, per quanto riguarda il resto dobbiamo moltiplicare per {2} il resto ottenuto, ovvero per il coefficiente del termine in {x} del polinomio divisore di partenza. In tal modo avremo il resto della divisione inizialmente data.
Per quanto riguarda la divisione con la regola di Ruffini è tutto. Nella prossima lezione ci occuperemo delle definizioni di funzioni polinomiali e polinomi identici, per poi passare alla scomposizione dei polinomi. Buon proseguimento con SìMatematica!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
