Veniamo ora a particolari disequazioni dette disequazioni prodotto. Si tratta di un particolare tipo di disequazioni di grado superiore al primo ma risolvibili sfruttando ciò che già sappiamo sulle disequazioni di primo grado.
Vedremo quindi come risolvere le disequazioni con prodotto (o disequazioni prodotto), ovvero particolari disequazioni algebriche che in forma normale si presentano come:
P(x) \lesseqgtr 0
ove {P(x)} è un polinomio scomponibile nel prodotto di fattori dati da polinomi tutti di primo grado, o comunque di grado non superiore al primo.
Così scomponendo il polinomio a primo membro ci ritroveremo con disequazioni nella forma:
P_1(x) \cdot P_2(x) \cdot P_3(x) \cdot \dots \cdot P_n(x)
ove avremo fattori in numero uguale al grado del polinomio {P(x)}.
Abbiamo visto come scomporre i polinomi nelle lezioni dedicate alla scomposizione dei polinomi. E con tali tecniche potremo scomporre in fattori il polinomio {P(x)} presente nelle disequazioni prodotto.
Come risolvere le disequazioni prodotto
Mostreremo come risolvere le disequazioni prodotto distinguendo il caso di un prodotto al primo membro dato da due soli fattori e il caso di un prodotto dato da più di due fattori. Precisiamo comunque che la tecnica che presenteremo nel caso dai tre fattori in su è comunque convenientemente applicabile anche al caso di un prodotto al primo membro con due soli fattori.
Disequazioni prodotto con due fattori al primo membro
Vediamo come risolvere disequazioni della forma:
P_1(x)\cdot P_2(x) \lesseqgtr 0
ove {P_1(x)} e {P_2(x)} sono polinomi di primo grado. Consideriamo ad esempio una disequazione con prodotto del tipo:
P_1(x) \cdot P_2(x) > 0
In questo caso richiediamo che il prodotto al primo membro sia positivo. Ma dall’algebra dei segni sappiamo che un prodotto tra due fattori è positivo se i due fattori sono concordi, ovvero hanno lo stesso segno.
Di conseguenza, la disequazione sarà verificata per {P_1(x) } e {P_2(x)} entrambi positivi oppure per {P_1(x)} e {P_2(x)} entrambi negativi. In simboli:
P_1(x) \cdot P_2(x) > 0 \iff \begin{cases}P_1(x) > 0 \\ \\ P_2(x) > 0 \end{cases} \quad \vee \quad \begin{cases} P_1(x) < 0 \\ \\ P_2(x) < 0 \end{cases}Osserviamo che ci ritroviamo con due sistemi da risolvere, e che la disequazione di partenza sarà soddisfatta dall’unione tra le soluzioni dei due sistemi (infatti il simbolo {\vee} significa “oppure”). E ciascun sistema sarà a sua volta soddisfatto dall’intersezione tra gli insiemi delle soluzioni di ciascuna disequazione di primo grado presente a sistema.
Capiamo quindi come sfruttando quanto sappiamo circa le disequazioni di primo grado siamo anche in grado di risolvere le disequazioni prodotto così come le abbiamo qui definite.
Esempio 1
Risolvere la seguente disequazione:
x^2+2x-3 > 0
Ci ritroviamo con una disequazione in forma normale di secondo grado, poiché il grado del polinomio al primo membro è uguale a {2}. Tuttavia, vediamo se è possibile scomporre il polinomio nel prodotto tra polinomi di primo grado.
Ricordando ad esempio la regola del trinomio caratteristico abbiamo:
x^2+2x-3 = (x+3)(x-1)
Così la disequazione di partenza diviene:
(x+3)(x-1) > 0
Ci ritroviamo così con una disequazione prodotto, con prodotto dato da due polinomi di primo grado.
L’equazione sarà soddisfatta per:
\begin{cases}x+3 > 0 \\ \\ x-1 > 0\end{cases} \quad \vee \quad \begin{cases} x +3 < 0 \\ \\ x - 1 < 0 \end{cases}Il problema non è complicato come sembrerebbe: basta risolvere prima di tutto ciascun sistema. Cominciamo dal primo:
\begin{cases}x+3 > 0 \\ \\ x-1 > 0 \end{cases}Sfruttando le proprietà delle disequazioni possiamo riscrivere il sistema come:
\begin{cases} x > -3 \\ \\ x > 1 \end{cases}E’ immediato osservare che tutti i valori della {x} maggiori di {1} sono anche maggiori di {-3}, valore che infatti è più piccolo di {1}. Così il sistema è soddisfatto da tutti i valori della {x} maggiori di {1}. Se comunque questo modo di ragionare più rapido vi crea confusione, possiamo ragionare su ciascuna singola disequazione.
In particolare, l’idea è quella di rappresentare graficamente gli insiemi delle soluzioni di ciascuna disequazione a sistema, per poi intersecare tra loro detti insiemi. Abbiamo:
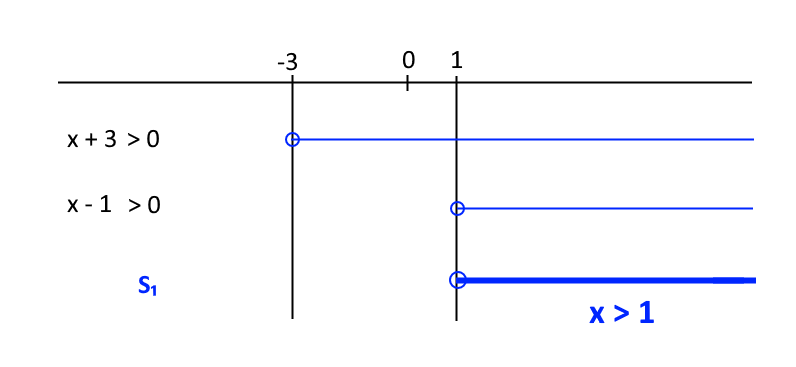
L’insieme delle soluzioni del sistema è in pratica dato da tutti quei punti nei quali, se tracciamo una retta verticale in corrispondenza di essi, incontriamo entrambe le semirette soluzioni delle due disequazioni a sistema.
Allo stesso modo possiamo risolvere il secondo sistema:
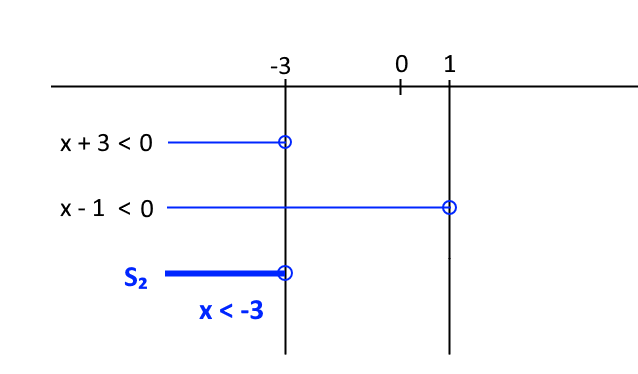
Concludiamo unendo gli insiemi delle soluzioni dei due sistemi. In altre parole, dovremo prendere come soluzioni della disequazione di partenza sia le soluzioni del primo sistema, sia le soluzioni del secondo sistema.
Così in definitiva la disequazione con prodotto di partenza ha il seguente insieme delle soluzioni:
x < -3 \quad \vee \quad x > 1
ovvero l’insieme dei valori della {x} minori di {-3} e i valori della {x} maggiori di {1}. Osserviamo che i valori {-3} ed {1} sono esclusi dall’insieme delle soluzioni della disequazione, in quanto in essa è esclusa l’uguaglianza (nella disequazione di partenza abbiamo infatti il simbolo di “maggiore”, e non di “maggiore o uguale”).
Disequazioni prodotto con più di tre fattori al primo membro
Consideriamo ora disequazioni prodotto (o disequazioni con prodotto) del tipo la seguente:
P_1(x) \cdot P_2(x) \: \cdot \dots \: \cdot P_n(x) \lesseqgtr 0, \qquad n > 2
ove {P_1(x), \: P_2(x), \dots, \: P_n(x)} sono tutti polinomi di primo grado. Intendiamo cioè il caso di disequazioni del tipo {P(x) \lesseqgtr 0} ove {P(x)} è riesprimibile come il prodotto di tre o più polinomi di primo grado.
In questo caso non conviene ragionare direttamente con l’algebra dei segni e considerare tutti i possibili casi come fatto nel caso precedente. Infatti la presenza di più fattori renderebbe i discorsi da fare piuttosto articolati.
L’idea è allora quella di studiare il segno di tutti i singoli fattori in uno stesso diagramma, e quindi applicare l’algebra dei segni a ciascun intervallo di valori della {x} individuabile nel diagramma stesso. In tal modo sarà possibile ricavare l’insieme delle soluzioni della disequazione in base al segno del polinomio {P(x)}. Basterà infatti tenere conto del particolare simbolo di disuguaglianza presente nella disequazione data e ragionare di conseguenza.
Ovviamente come nei casi precedenti la prima cosa da fare sarà accertarsi che la disequazione da risolvere sia in forma normale. Diversamente basterà comunque utilizzare le proprietà delle disequazioni in modo da ricondursi a tale forma.
Vediamo subito un esempio.
Esempio 2 (disequazione prodotto con tre fattori)
Risolvere la seguente disequazione:
(x-5)(x+1)(x+3) \geq 0
Ci ritroviamo con una disequazione prodotto già in forma normale (infatti il secondo membro è zero). Al primo membro abbiamo il prodotto fra tre polinomi di primo grado.
Cominciamo studiando il segno di ciascun fattore, su di uno stesso diagramma:
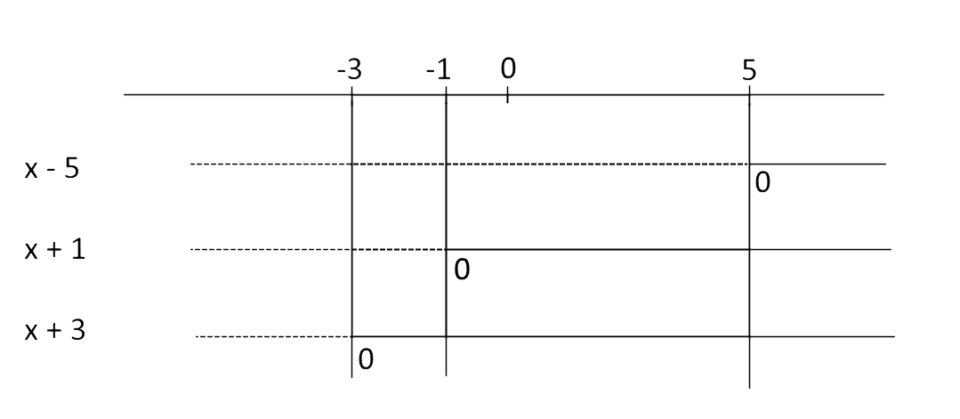
Ricordiamo che la linea tratteggiata indica il segno meno, mentre la linea continua indica il segno più. Abbiamo inoltre posto uno zero in corrispondenza del valore che annulla il fattore considerato (attenzione, si tratta di uno zero e non di un pallino vuoto).
E’ immediato osservare che il diagramma consente di individuare quattro intervalli di valori per la {x}, che indichiamo con i numeri romani:
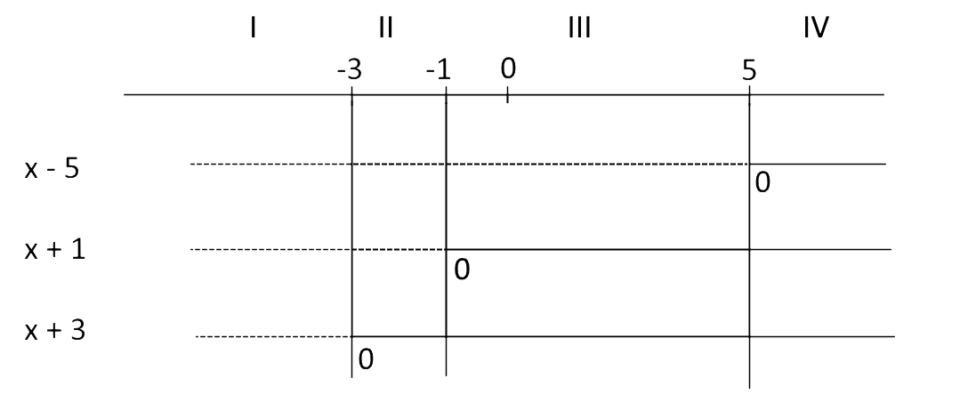
Ora procediamo scrivendo il segno in corrispondenza di ciascun intervallo, per ogni fattore:
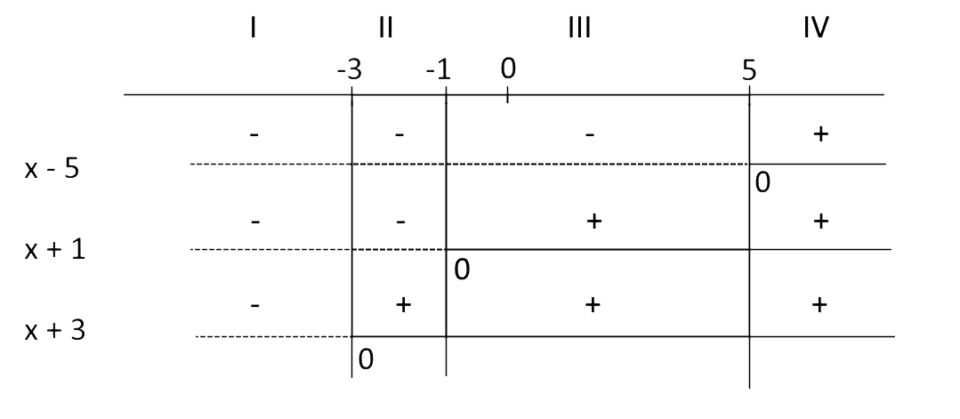
Ora, il nostro obiettivo è determinare il segno del prodotto {(x-5)(x+1)(x+3)} in ciascun intervallo. Ma per fare questo basterà utilizzare l’algebra dei segni.
Nel primo intervallo, ad esempio, vediamo che il fattore {x-5} ha segno negativo, il fattore {x+1} ha segno meno e infine il fattore {x+3} ha pure segno meno. Così, per l’algebra dei segni nel primo intervallo il prodotto {(x-5)(x+1)(x+3)} avrà segno meno per meno per meno, e quindi meno.
Procedendo allo stesso modo per ciascun intervallo sarà possibile determinare il segno del prodotto {(x-5)(x+1)(x+3)} anche per i rimanenti intervalli. Complessivamente avremo:
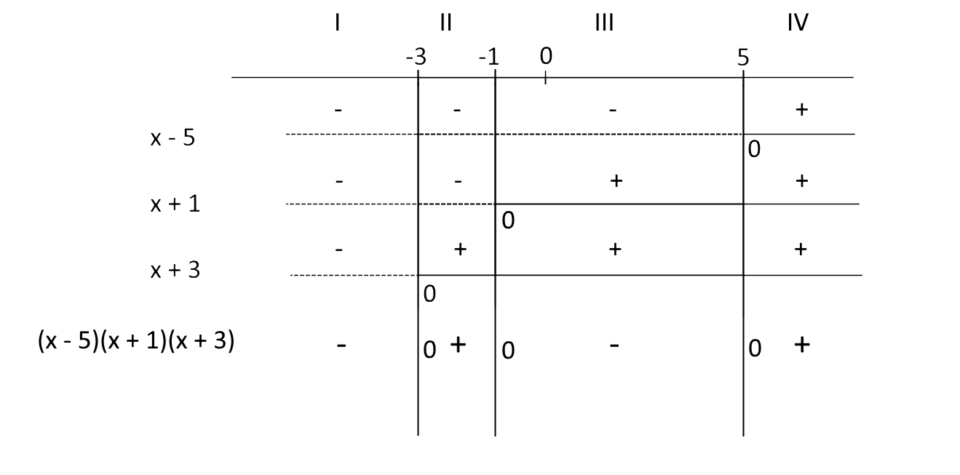
Così ad esempio nel terzo intervallo il prodotto {(x-5)(x+1)(x+3)} è negativo. Osserviamo che abbiamo di nuovo scritto uno zero in corrispondenza dei valori della {x} che annullano un fattore. Infatti, laddove si annulla almeno uno dei fattori del prodotto si annulla anche il prodotto stesso.
Osservazione. L’ultimo diagramma riportato rappresenta lo studio del segno di un prodotto e fornisce il segno assunto dal prodotto stesso per ciascun intervallo di valori della {x}.
A questo punto ci rimane da trarre le conclusioni finali in base alla disequazione data. Essa richiede che il prodotto {(x-5)(x+1)(x+3)} sia maggiore di zero o anche uguale a zero (infatti è compresa anche l’uguaglianza, avendo il simbolo di maggiore o uguale). Così, l’insieme delle soluzioni della disequazione sarà dato da tutti i valori della {x} che rendono positivo o nullo il prodotto al primo membro. Di conseguenza rappresentando graficamente l’insieme delle soluzioni della disequazione avremo:
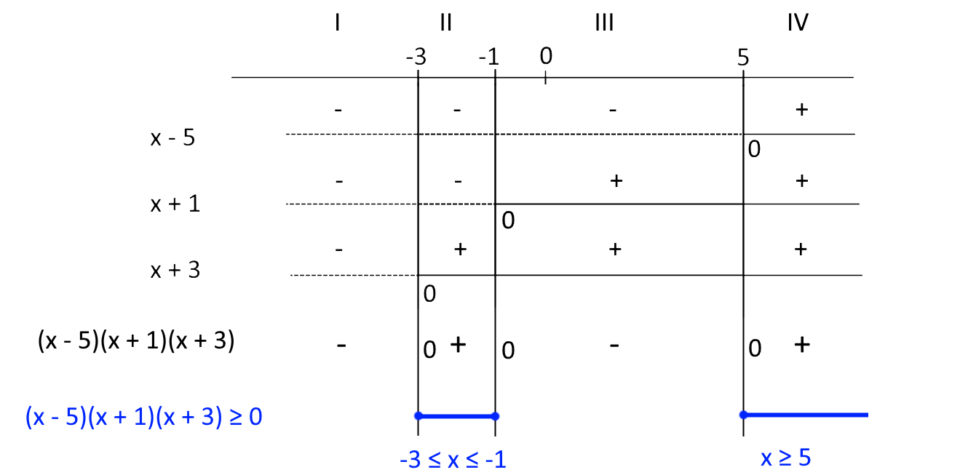
Ciò significa che la disequazione è soddisfatta per i valori della {x} compresi fra {-3} e {-1} (estremi inclusi) e per i valori della {x} maggiori o uguali a {5}. Osserviamo che abbiamo posto in corrispondenza dei valori {-3}, {-1} e {5} un pallino pieno, in quanto tali valori appartengono all’insieme delle soluzioni della disequazione. Così in conclusione la disequazione ammette le soluzioni:
-3 \leq x \leq -1 \quad \vee \quad x \geq 5
Importante. Abbiamo qui proposto un possibile metodo per rappresentare graficamente i segni dei fattori del prodotto e il segno del prodotto stesso nei vari intervalli. Tuttavia, consigliamo di seguire le convenzioni utilizzate dal vostro insegnante. In particolare, generalmente viene già indicato nello studio del segno di ciascun fattore se gli zeri sono compresi oppure no nell’insieme delle soluzioni della disequazione. Abbiamo tuttavia qui preferito limitarci inizialmente ad indicare gli zeri di ciascun fattore ponendo il simbolo dello zero, per poi stabilire se sono compresi o meno nell’insieme delle soluzioni soltanto alla fine. In tal modo lo studio del segno prescinde dal particolare simbolo di disuguaglianza presente nella disequazione data.
Come detto il metodo appena presentato può anche essere applicato al caso di un prodotto {P(x)} dato da due soli fattori. Riprendiamo allora la disequazione già risolta in precedenza:
x^2+2x-3 > 0
Riscriviamo il primo membro come prodotto di due fattori:
(x+3)(x-1) > 0
A questo punto riportiamo gli studi dei segni dei fattori in uno stesso diagramma, per poi individuare l’insieme delle soluzioni della disequazione come visto nel caso di tre o più fattori:
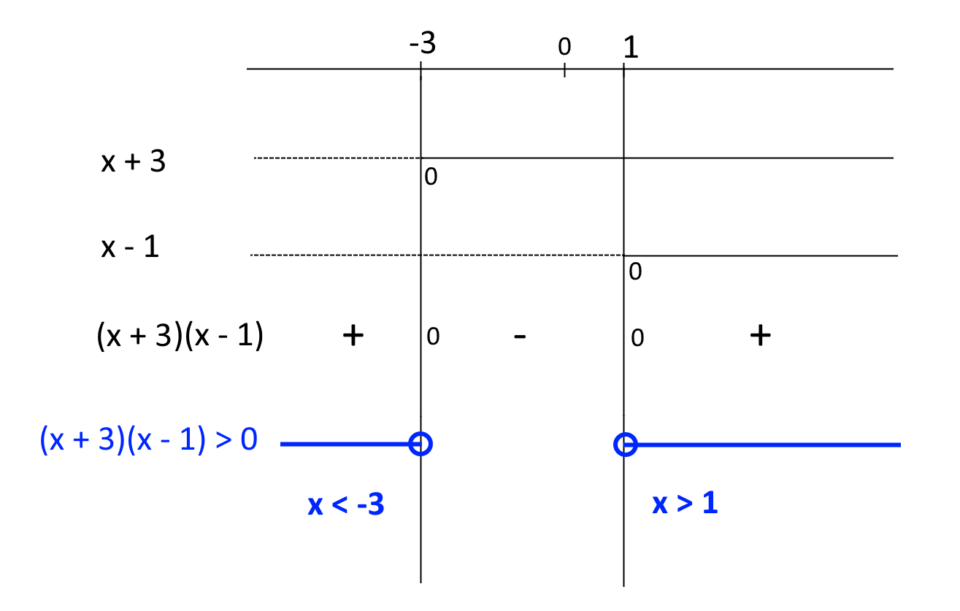
Ritroviamo così l’insieme delle soluzioni:
x < -3 \quad \vee \quad x > 1
Osserviamo infine che, nella rappresentazione grafica dell’insieme delle soluzioni, i pallini vuoti riportati in corrispondenza dei valori {-3} e {1} significano che tali valori devono essere esclusi dall’insieme delle soluzioni. Infatti, nella disequazione di partenza abbiamo il simbolo di “maggiore” e non “maggiore o uguale”.
Conclusioni
Per quanto riguarda le disequazioni prodotto è tutto. Abbiamo visto come grazie allo studio del segno del prodotto {P(x)} al primo membro di una disequazione ridotta in forma normale è possibile individuare l’insieme delle soluzioni della disequazione.
Buon proseguimento con SìMatematica!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
