Semiretta e segmento

 - 

Domini piani

Una semiretta e un segmento possono essere visti come l’intersezione tra una retta e un opportuno dominio piano. In particolare, una semiretta può essere data dall’intersezione tra un semipiano, avente per origine una retta r₁, e una retta r tale che le due rette r e r₁ si intersechino in un certo punto T. Invece, un segmento può essere ottenuto dall’intersezione tra una striscia σ e una retta r che non sia parallela ai lati della striscia.

Dopo aver visto nelle precedenti lezioni come ottenere un dominio piano a partire da delle rette, in questa lezione vedremo come sia possibile ottenere una semiretta o un segmento a partire da un opportuno dominio piano, intersecandolo con una certa retta.

Vediamo allora subito degli esercizi di esempio su come ottenere un segmento o una semiretta dall’intersezione di una retta e di un opportuno dominio piano (semipiano o striscia).

Semiretta

Vediamo come riguardare una semiretta o un segmento come l’intersezione tra una retta ed un opportuno dominio piano a partire dal caso della semiretta.

L’intersezione tra una retta {r} e un semipiano {\alpha_1} di origine {r_1} è data da una semiretta di origine {T}, ove {T} è il punto di intersezione delle rette {r} e {r_1}, che supponiamo incidenti.

Indichiamo tale semiretta con {Tr} (vedi figura a seguire).

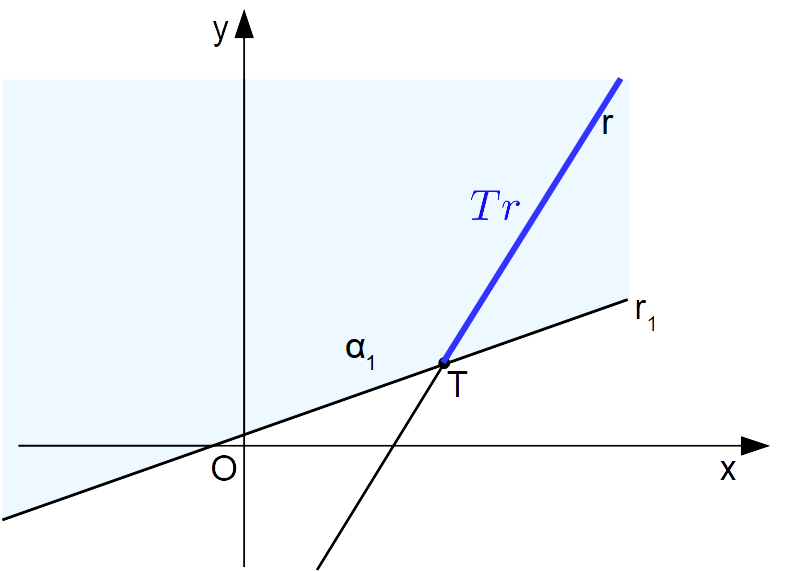
Osservazione. Ricordiamo che due rette del piano cartesiano sono incidenti se sono non parallele ed hanno quindi un punto in comune. Precisiamo invece che due rette nello spazio possono essere non parallele ma comunque essere o incidenti, o sghembe.

Così, data la retta {r} di equazione:

r: ax+by+c=0

e il semipiano {\alpha_1} di equazione:

\alpha_1 : a_1x +b_1y+c_1 \lesseqgtr 0 

la semiretta di origine {T}, che indichiamo con {Tr}, i cui punti appartengono tutti al semipiano {\alpha_1}, è data da:

Tr= \alpha_1 \cap r: \begin{cases} r:ax+by+c= 0 \\ \\ \alpha_1 :  a_1x+b_1y+c_1 \lesseqgtr 0\end{cases}

La retta origine del semipiano {\alpha_1} per quanto visto in una precedente lezione ha equazione:

r_1 : a_1 x + b_1 y + c_1 = 0 

Di conseguenza, affinché l’intersezione tra il semipiano {\alpha_1} e la retta {r} sia data da una semiretta, dovrà valere la condizione:

\det \begin{pmatrix} a & b \\  a_1 & b_1  \end{pmatrix}=a \cdot b_1 - a_1 \cdot b \neq 0

che esprime il non parallelismo tra la retta {r} e la retta {r_1} origine del semipiano {\alpha_1}.

Esempio (semiretta come intersezione tra un semipiano ed una retta)

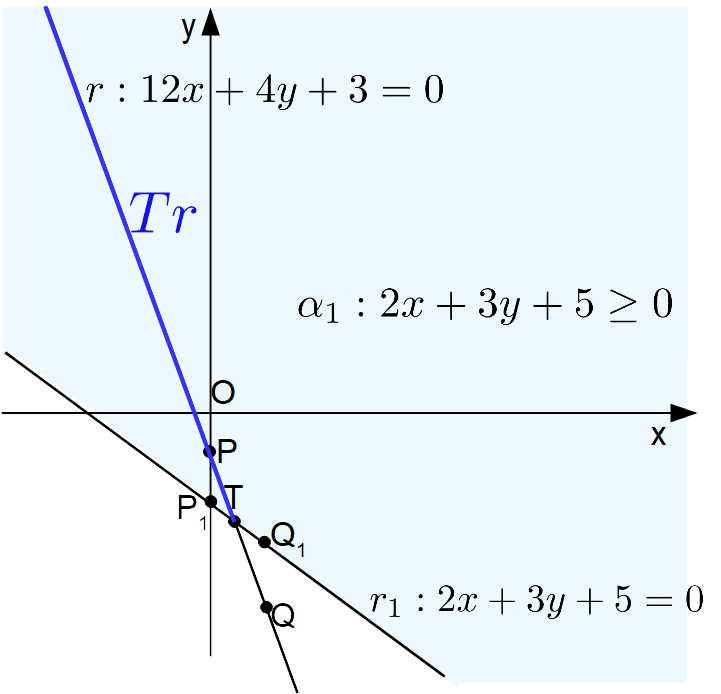
Stabilire se si ottiene una semiretta dall’intersezione del semipiano {\alpha_1 : 2x+3y+5 \geq 0 } e della retta {r: 12x+4y+3=0} .

Osserviamo che la retta {r_1} origine del semipiano {\alpha_1} ha equazione:

r_1 : 2x+3y+5 = 0 

Date le equazioni delle rette {r} ed {r_1}, abbiamo:

a=12, \: b=4, \: a_1 = 2, \: b_1 = 3

Di conseguenza:

\det \begin{pmatrix} a & b \\ a_1 & b_1\end{pmatrix}=\det \begin{pmatrix} 12 & 4 \\ 2 & 3\end{pmatrix}=12\cdot3 -2 \cdot 4 = 28 \neq 0

Poiché il determinante appena calcolato è non nullo, le due rette sono non parallele. E poiché stiamo lavorando nel piano cartesiano, le due rette sono incidenti.

Ma allora l’intersezione tra la retta {r} e il semipiano {\alpha_1} dovrà dar luogo ad una semiretta avente per origine il punto di intersezione {T} tra la retta {r} e la retta {r_1} origine del semipiano {\alpha_1}.

Cominciamo tracciando entrambe le rette {r} ed {r_1} nel piano cartesiano. Come visto nelle precedenti lezioni, il primo passo consiste nel rappresentare le rette in forma esplicita (ricavando cioè un’espressione per la {y}):

\begin{align*} & r_1 : 2x+3y+5 = 0 \quad \Rightarrow \quad y=-\dfrac{2}{3}x-\dfrac{5}{3} \\ \\& r: 12x+4y+3=0 \quad \Rightarrow \quad y=-3x-\dfrac{3}{4}\end{align*}

Ora basta ottenere le coordinate di due punti qualsiasi di ciascuna retta. Per {r_1} abbiamo ad esempio:

P_1=(0, -5/3), \qquad Q_1=(1, -7/3)

mentre per la retta {r}:

P=(0,-3/4), \qquad  Q =(1, -15/4)

Adesso non resta che disegnare nel piano cartesiano le rette passanti per i punti {P_1, \: Q_1} e per i punti {P, \: Q}:

Il punto {T}, dato dall’intersezione tra le rette {r_1} e {r}, ha coordinate tali da soddisfare il seguente sistema:

\begin{cases} 12x+4y+3=0 \\ \\ 2x+3y+5=0\end{cases}

Risolvendo il sistema per riduzione possiamo determinare le coordinate del punto {T}:

\begin{align*} & \begin{cases} 12x+4y+3=0 \\ \\ 12x+18y+30=0\end{cases} \quad \Rightarrow \quad \begin{cases} 12x+4y+3=0 \\ \\ -14y-27=0\end{cases} \quad \Rightarrow \\ \\ 
 & \Rightarrow \quad \begin{cases}x=\dfrac{11}{28}\\ \\ y=-\dfrac{27}{14} \end{cases} \end{align*}

Dobbiamo ora individuare il semipiano {\alpha_1}. Per fare questo, vediamo ad esempio se il punto {P} in figura soddisfa la disequazione relativa al semipiano {\alpha_1}:

\alpha_1 : 2x+3y+5 \geq 0

Il punto {P} ha coordinate {(0, -3/4)} e si trova al di sopra della retta {r_1}. Così, se le coordinate del punto {P} soddisfano la disequazione appena scritta, allora il semipiano {\alpha_1} è dato da tutti i punti del piano al di sopra della retta {r_1}. Abbiamo:

\begin{align*} & 2x+3y+5 \geq 0 \quad \text{con} \quad x=0, \: y=-3/4  \\ \\ & 2 \cdot 0 + 3 \cdot \left( -\dfrac{3}{4}\right)+5 \geq 0 \quad \Rightarrow \quad \dfrac{11}{4} \geq 0  \quad \text{OK} \end{align*}

Di conseguenza il semipiano {\alpha_1} è dato da punti tutti al di sopra di {r_1}:

E in conclusione, l’intersezione tra la retta {r} e il semipiano {\alpha_1} è l’insieme dei punti tali da soddisfare il sistema:

Tr: \begin{cases}\alpha_1 : 2x+3y+5 \geq 0 \\ \\  r: 12x+4y+3=0 \end{cases}

ovvero è l’insieme dei punti della retta {r} tali da appartenere anche al semipiano {\alpha_1}. Così otteniamo la semiretta {Tr}, ovvero la semiretta avente origine in {T=\left( \dfrac{11}{28}, -\dfrac{27}{14}\right)} e passante per {P}, che possiamo rappresentare graficamente come segue:

Segmento (semiretta e segmento come intersezione tra un dominio piano e una retta)

Possiamo riguardare un segmento come l’intersezione tra una striscia {\sigma} e una retta {r} non parallela ai lati della striscia.

Osserviamo che per “lati” della striscia {\sigma} intendiamo le rette {r_1} ed {r_2} che delimitano la striscia stessa.

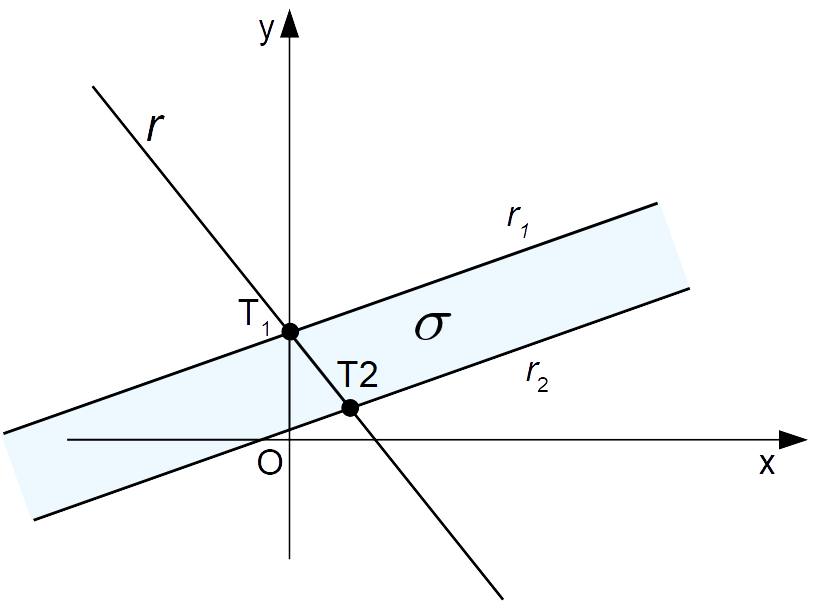
Così il segmento {\overline{T_1T_2}} è dato dall’intersezione della striscia {\sigma} con la retta {r}.

Se dunque la retta {r} ha equazione:

r: ax+by+c=0

e le rette che delimitano la striscia {\sigma} (tra loro parallele) hanno equazioni:

\begin{align*} &r_1 : a_1x+b_1y+c_1=0 \\ \\ &r_2 : a_1x+b_1y+c_2=0\end{align*}

allora deve valere la seguente condizione di non parallelismo tra la retta {r} e le rette {r_1, \: r_2}:

\det \begin{pmatrix} a & b \\ a_1 & b_1 \end{pmatrix} =a \cdot b_1 - a_1 \cdot b \neq 0

Solo se vale questa condizione l’intersezione tra la striscia {\sigma} e la retta {r} sarà data da un segmento.

Infine, le coordinate degli estremi del segmento saranno date dalle coppie {(x,y)} soluzioni rispettivamente dei sistemi:

\begin{cases} r: ax+by+c=0 \\ \\ r_1 : a_1x+b_1y+c_1=0\end{cases}; \qquad \begin{cases} r: ax+by+c=0 \\ \\ r_2: a_1x+b_1y+c_2=0\end{cases}

Infatti, ciascun estremo del segmento è un punto dato dall’intersezione di uno dei lati della striscia {\sigma} con la retta {r}.

Esempio (segmento come intersezione tra una striscia e una retta)

Verificare se è possibile ottenere un segmento dall’intersezione della striscia {\sigma : -2 \leq 2x+3y \leq 4} con la retta {r: 5x+9y = 0}. Eventualmente indicare le coordinate degli estremi del segmento.

Cominciamo controllando se la retta {r} è parallela o meno ai lati della striscia {\sigma}. Anzitutto, osserviamo che la striscia {\sigma} è esprimibile come:

\sigma : -2 \leq 2x+3y \leq  4 \iff \begin{cases} \alpha_1 : 2x+3y \geq -2 \\ \\ \alpha_2 : 2x+3y \leq  4\end{cases}

Abbiamo in particolare ricondotto la doppia disequazione che rappresenta la striscia {\sigma} ad un sistema di due disequazioni. Ricordiamo infatti che una striscia è ottenibile come intersezione di due semipiani aventi come origini delle rette tra loro parallele. Ora, le rette origini dei semipiani {\alpha_1} e {\alpha_2} sono:

r_1 : 2x+3y+2 = 0; \qquad r_2 : 2x+3y-4=0

Vediamo se la retta {r} è parallela o meno a tali rette:

\det \begin{pmatrix} a & b \\ a_1 & b_1 \end{pmatrix}=a \cdot b_1-a_1 \cdot b = 5 \cdot 3 -2 \cdot 9=15-18 \neq 0

I coefficienti {a} e {b} sono i coefficienti dei termini in {x} nell’equazione della retta {r}, mentre i coefficienti {a_1} e {b_1} sono i coefficienti dei termini in {x} e {y} della retta {r_1}, che assieme alla retta {r_2} delimita la striscia {\sigma}. Osserviamo che la retta {r_2} presenta questi stessi coefficienti per i termini in {x} e {y} che figurano nella corrispondente equazione.

La retta {r} è dunque non parallela ai lati della striscia {\sigma}. Di conseguenza, l’intersezione tra la striscia {\sigma } e la retta {r} è necessariamente data da un segmento.

Per calcolare le coordinate degli estremi di tale segmento, dobbiamo intersecare la retta {r} con la retta {r_1} e poi con la retta {r_2}. Così scriviamo intanto:

r \cap r_1: \begin{cases}5x+9y=0 \\ \\ 2x+3y+2=0 \end{cases}

Risolviamo il sistema per riduzione:

\begin{cases} 5x+9y=0 \\ \\ -x-6=0 \quad \rightarrow \quad x=-6\end{cases} \quad \Rightarrow \quad \begin{cases}y = \dfrac{10}{3} \\ \\  x=-6\end{cases}

Così un primo estremo del segmento è dato dal punto {T_1 = (-6, 10/3)}.

Determiniamo infine le coordinate del secondo estremo del segmento:

r \cap r_2 :\begin{cases}5x+9y=0 \\ \\ 2x+3y-4=0 \end{cases}

Risolviamo anche in questo caso il sistema per riduzione:

\begin{cases} 5x+9y=0 \\ \\ -x +12=0 \quad \rightarrow x=12\end{cases} \quad \Rightarrow \quad \begin{cases} y=-\dfrac{20}{3}\\ \\ x=12\end{cases}

In conclusione il rimanente estremo del segmento è dato dal punto {T_2=(12, -20/3)}.

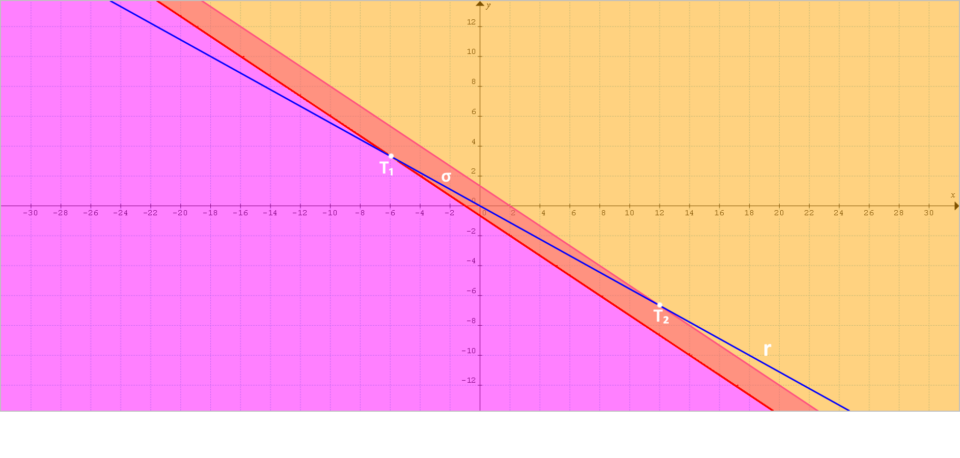
Per questa lezione su retta e segmento come intersezione tra una retta ed un opportuno dominio piano è tutto. Nella prossima lezione vedremo come determinare il massimo e il minimo di una funzione lineare in un dominio piano dato da un poligono. Buono studio a tutti voi! 🙂