In questa lezione ci occupiamo di come calcolare il cubo di un trinomio e il cubo di un quadrinomio. Nell’eseguire tali operazioni utilizzeremo due differenti approcci che ci permetteranno di utilizzare gli strumenti che abbiamo già a disposizione.
In particolare, il cubo di un trinomio può essere ricondotto al prodotto fra il quadrato del trinomio e il trinomio stesso. E ciò è possibile grazie alle proprietà delle potenze.
Allo stesso modo, sarà possibile ricondurre il cubo di un quadrinomio al prodotto del quadrato del quadrinomio per il quadrinomio stesso. Tuttavia, questa strada non appare molto pratica. Di conseguenza, per il calcolo del cubo di un quadrinomio cercheremo piuttosto di ricondurci al caso del cubo di un binomio, operando opportune sostituzioni.
Inoltre, anche per quanto riguarda il cubo di un trinomio è possibile ricondursi al caso del cubo di un binomio sempre operando opportune sostituzioni. Per cui per questo caso mostreremo due differenti metodi per il suo calcolo.
Infine, precisiamo che per il cubo di un trinomio è anche possibile definire una regola in stile “prodotto notevole”. Tuttavia, quest’ultima strada non è molto utilizzata in quanto la regola che si ottiene è piuttosto scomoda da utilizzare.
Come calcolare il cubo di un trinomio
Consideriamo il cubo di un trinomio nella forma più generale:
(a+b+c)^3
Per le proprietà delle potenze si ha:
(a+b+c)^3=(a+b+c)^2\cdot(a+b+c)
E’ dunque possibile calcolare il cubo di un trinomio come prodotto del quadrato del trinomio per il trinomio stesso.
Esempio
Calcolare:
(2xy+3x^2-4x^2y)^3
Per le proprietà delle potenze abbiamo:
(2xy+3x^2-4x^2y)^3=(2xy+3x^2-4x^2y)^2 \cdot (2xy+3x^2-4x^2y)=
Si tratterà quindi di calcolare il quadrato del trinomio e quindi eseguire il prodotto tra polinomi (quest’ultimo nel caso in esame piuttosto scomodo):
\begin{align*} & =(4x^2y^2+9x^4+16x^4y^2+12x^3y-24x^4y-16x^3y^2)\cdot(2xy+3x^2-4x^2y)=\\ \\ & = 8x^3y^3+18x^5y+32x^5y^3+24x^4y^2-48x^5y^2-32x^4y^3+\\ \\ & +12x^4y^2+27x^6+48x^6y^2+36x^5y-72x^6y-48x^5y^2+\\ \\ & -16x^4y^3-36x^6y-64x^6y^3-48x^5y^2+96x^6y^2+64x^5y^3 = \\ \\ & =8x^3y^3+(18+36)x^5y+(32+64)x^5y^3+(24+12)x^4y^2+\\ \\ & +(-48-48-48)x^5y^2+(-32-16)x^4y^3+27x^6+(48+96)x^6y^2+\\ \\ & -64x^6y^3+(-72-36)x^6y = \\ \\ & =8x^3y^3+54x^5y+96x^5y^3+36x^4y^2-144x^5y^2-48x^4y^3+27x^6+144x^6y^2+\\ \\ & -64x^6y^3-108x^6y\end{align*}I calcoli sono piuttosto noiosi ma osserviamo che se avessimo calcolato il cubo di partenza come:
(2xy+3x^2-4x^2y)^3=(2xy+3x^2-4x^2y)(2xy+3x^2-4x^2y)(2xy+3x^2-4x^2y)
ci saremmo ritrovati con dei calcoli ancora più complicati.
Il metodo alternativo consiste nell’utilizzare delle sostituzioni. Ripartiamo dal problema di partenza:
(2xy+3x^2-4x^2y)^3
Ponendo {A=2xy+3x^2} e {B=-4x^2y} ci ritroviamo con il seguente cubo di un binomio:
(A+B)^3=A^3+3A^2B+3AB^2+B^3=
ovvero sostituendo a ciascuna lettera l’espressione corrispondente:
\small \begin{align*} & =(2xy+3x^2)^3+3 (2xy+3x^2)^2(-4x^2y)+3(2xy+3x^2)(-4x^2y)^2+(-4x^2y)^3= \\ \\ & = 8x^3y^3+3\cdot(2xy)^2\cdot3x^2+3 \cdot 2xy\cdot(3x^2)^2 +27x^6+3(4x^2y^2+\\ \\ & +12x^3y+9x^4)(-4x^2y)+(6xy+9x^2)16x^4y^2-64x^6y^3=\\ \\ & =8x^3y^3+3\cdot4x^2y^2\cdot3x^2+6xy\cdot9x^4+27x^6+3(-16x^4y^3-48x^5y^2-36x^6y)+\\ \\ & +96x^5y^3+144x^6y^2-64x^6y^3 = \\ \\ & =8x^3y^3+36x^4y^2+54x^5y+27x^6-48x^4y^3-144x^5y^2-108x^6y+\\ \\ & +96x^5y^3+144x^6y^2-64x^6y^3\end{align*}Come calcolare il cubo di un quadrinomio
Proviamo a calcolare il seguente cubo di un quadrinomio:
(a+2b+ab+b^2)^3
Riscriviamo l’espressione di partenza come segue:
[(a+2b)+(ab+b^2)]^3
In questo modo ponendo {A=a+2b} e {B=ab+b^2} ci riconduciamo al cubo di un binomio:
(A+B)^3=A^3+3A^2B+3AB^2+B^3
ovvero, sostituendo a ciascuna lettera l’espressione corrispondente:
(a+2b)^3+3 (a+2b)^2(ab+b^2)+3 (a+2b)(ab+b^2)^2+(ab+b^2)^3
L’espressione è abbastanza lunga da calcolare ma in ogni caso consente di arrivare al risultato desiderato dovendo calcolare unicamente quadrati e cubi di binomi e prodotti fra polinomi, questi ultimi più agevoli da calcolare rispetto al prodotto {(a+2b+ab+b^2)(a+2b+ab+b^2)(a+2b+ab+b^2)}.
Per brevità omettiamo i passaggi. Otteniamo il risultato finale:
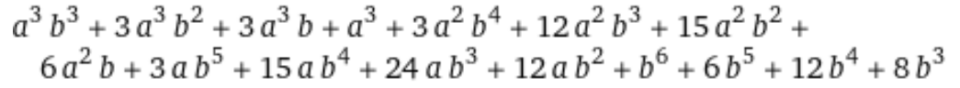
Per questa lezione è tutto. Nella prossima ci occuperemo dei prodotti notevoli della somma di cubi e della differenza di cubi. Buono studio!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
