Esercizi sulle equazioni di secondo grado parametriche

 - 

Equazioni (superiori)

Vediamo ora degli esercizi sulle equazioni di secondo grado parametriche (o letterali). Come abbiamo visto nella lezione teorica, si tratta di equazioni di secondo grado che oltre a contenere l’incognita {x} presentano altre lettere dette parametri. Così le soluzioni di un’equazione parametrica non saranno più soluzioni numeriche ma bensì soluzioni letterali (soluzioni parametriche). In altre parole, le eventuali soluzioni dell’equazione saranno espresse in funzione del parametro o dei parametri presenti.

Ora, poiché in generale le equazioni di secondo grado ammettono soluzioni o meno in funzione del valore del discriminante {\Delta}, nelle equazioni di secondo grado parametriche il discriminante dipende dal parametro. Di conseguenza, avremo soluzioni per un’equazione di secondo grado parametrica soltanto per i valori del parametro che rendono il discriminante maggiore o al più uguale a zero.

Fatte le dovute premesse, vediamo subito degli esercizi sulle equazioni di secondo grado parametriche, svolti e commentati.

Esercizi svolti e commentati sulle equazioni di secondo grado parametriche

Prima parte: esercizi di livello base (un solo parametro)

Esercizio 1

Discutere le soluzioni della seguente equazione di secondo grado letterale al variare del parametro {k}:

x^2+3kx = 0

Si tratta di un’equazione parametrica di secondo grado spuria. Dobbiamo quindi effettuare un raccoglimento per {x}:

x(x+3k)=0

Per la legge di annullamento del prodotto abbiamo:

x= 0 \quad \vee \quad x +3k = 0

Da cui otteniamo le soluzioni:

x_1 = 0 \quad \vee \quad x_2 =-3k, \qquad k \in \mathbb{R}

In questo particolare caso, poiché l’equazione è spuria abbiamo ottenuto una soluzione numerica e una soluzione parametrica. Infatti la soluzione {x_2} dipende dal valore reale del parametro {k}.

Esercizio 2

Discutere le soluzioni al variare del parametro {k} della seguente equazione:

x^2-(k+2)x=0

Siamo ancora in presenza di un’equazione di secondo grado parametrica spuria. Per cui raccogliamo la {x} e applichiamo la legge di annullamento del prodotto:

x[x-(k+2)]= 0

ovvero:

x(x-k-2)=0

e quindi in conclusione:

x_1=0 \quad \vee \quad x_2=k+2, \qquad k \in \mathbb{R}

Esercizio 3

Discutere le soluzioni della seguente equazione parametrica:

x^2-k^2 = 0

In questo caso abbiamo un’equazione pura. Ricordiamo infatti che il parametro deve essere considerato come un numero. Per cui nell’equazione abbiamo un solo termine contenente l’incognita, con esponente due.

Si ha:

x^2 = k^2 

e quindi estraendo la radice di entrambi i membri:

|x|=|k|

da cui otteniamo le soluzioni:

x_1 = -|k|=-k, \qquad x_2 = |k|=k, \qquad k \in \mathbb{R}

Osserviamo che abbiamo potuto eliminare i simboli di valore assoluto poiché una soluzione è l’opposta dell’altra.

Esercizio 4

Discutere le soluzioni dell’equazione:

4x^2-k^2+2k-1=0

Anche in questo caso siamo in presenza di un’equazione di secondo grado parametrica pura. Infatti, la quantità {-k^2+2k-1} contiene il solo parametro {k} ed è quindi il termine noto.

Abbiamo:

4x^2=k^2-2k+1

e quindi:

x^2 = \dfrac{k^2-2k+1}{4}

Estraendo la radice quadrata di entrambi i membri:

|x|=\sqrt{\dfrac{k^2-2k+1}{4}}

osserviamo che {k^2-2k+1=(k-1)^2}. Inoltre poiché la radice di una frazione è uguale al rapporto delle radici del numeratore e del denominatore, abbiamo:

|x|=\dfrac{\sqrt{k^2-2k+1}}{\sqrt{4}}=\dfrac{\sqrt{(k-1)^2}}{2}=\dfrac{|k-1|}{2}

da cui otteniamo le soluzioni:

x_1 = -\dfrac{|k-1|}{2};\qquad x_2 = \dfrac{|k-1|}{2}

Osserviamo che è possibile eliminare i simboli di valore assoluto. Infatti una soluzione è l’opposta dell’altra. Per cui abbiamo in conclusione:

x_1 = -\dfrac{k-1}{2}; \qquad x_2 = \dfrac{k-1}{2}

Esercizio 5

Proseguiamo gli esercizi sulle equazioni parametriche di secondo grado con il seguente:

x^2+x-k^2-3k-2=0

Osserviamo che l’equazione è in questo caso completa. Infatti abbiamo un termine in {x^2}, un termine in {x} e per il resto una quantità dipendente soltanto dal parametro {k} (ovvero, il termine noto {-k^2-3k-2}).

Abbiamo quindi {a=1, \: b = 1 } e {c=-k^2-3k-2}. Calcoliamo il determinante o discriminante {\Delta}:

\begin{align*} & \Delta = b^2-4ac=1^2-4 \cdot 1 \cdot (-k^2-3k-2) = \\ \\ & =1-4(-k^2-3k-2)= 1+4k^2+12k+8= \\ \\ & =4k^2+12k+9=(2k+3)^2 \end{align*}

Osserviamo che il discriminante corrisponde al quadrato di un binomio e quindi sarà positivo per ogni valore reale di {k}. Un’eccezione è dato dal valore del parametro tale da annullare la base {2k+3}:

2k+3 = 0 \iff k = -\dfrac{3}{2}

Per tale valore del parametro il discriminante si annulla e quindi avremo due soluzioni reali e coincidenti. Per tutti gli altri valori reali del parametro avremo invece per l’equazione due soluzioni reali e distinte.

Applichiamo la formula risolutiva generale delle equazioni di secondo grado, tenendo conto che abbiamo {a=1, \: b=1 } e {\Delta = (2k+3)^2}:

\begin{align*} & x_{1,2} = \dfrac{-1 \pm \sqrt{(2k+3)^2}}{2 \cdot 1}=\dfrac{-1 \pm |2k+3|}{2} = \\ \\ & =\begin{cases}\dfrac{-1+2k+3}{2}=\dfrac{2k+2}{2}=\dfrac{\cancel{2}(k+1)}{\cancel{2}}=k+1  \\ \\ \dfrac{-1-2k-3}{2}=\dfrac{-2k-4}{2}=\dfrac{2(-k-2)}{2}=-k-2\end{cases} \end{align*}

E queste sono le soluzioni dell’equazione di partenza per {k \in \mathbb{R}}.

Esercizio 6

Proseguiamo gli esercizi sulle equazioni di secondo grado parametriche con il seguente:

x^2+2kx+k^2=0

Abbiamo anche in questo caso un’equazione di secondo grado parametrica completa, con {a=1, \: b=2k} e {c=k^2}. Vediamo il discriminante:

\Delta = b^2-4ac=(2k)^2-4 \cdot 1 \cdot k^2=4k^2-4k^2=0

Il discriminante è uguale a zero, di conseguenza l’equazione ha due soluzioni uguali e coincidenti per ogni valore reale di {k}. Calcoliamole:

x_{1,2} = \dfrac{-b \pm \sqrt{\Delta}}{2a}=\dfrac{-2k \pm 0 }{2 \cdot 1}=-k, \qquad k \in \mathbb{R}

Seconda parte: esercizi sulle equazioni parametriche di secondo grado di livello intermedio (un parametro)

Esercizio 7

Risolvere:

x^2-6kx+9k=0

Abbiamo {a=1, \: b = -6k} e {c=9k}.

Calcoliamo il determinante o discriminante:

\Delta = b^2-4ac=\left( -6k\right)^2- 4 \cdot 1 \cdot 9k= 36k^2-36k=36k(k-1)

Si tratterà ora di vedere quando il discriminante è maggiore o uguale a zero, ovvero:

36k(k-1) \geq 0 

Per vedere questo, dobbiamo studiare il segno del prodotto {36k(k-1)} al variare di {k}. Procediamo per via grafica, studiando il segno dei singoli fattori e quindi determinando con l’algebra dei segni il segno del prodotto:

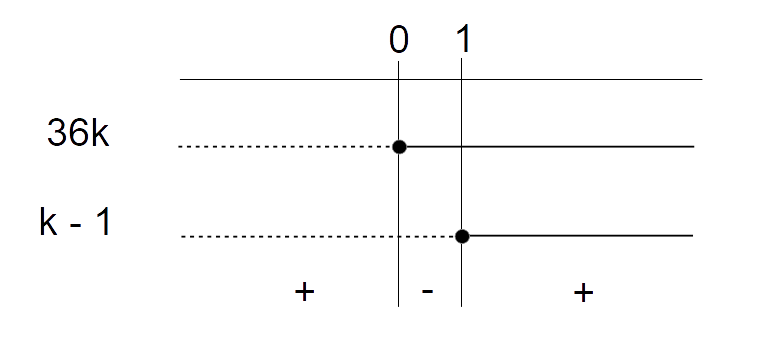
Il discriminante è dunque positivo o nullo per {k \leq 0 } oppure per {k \geq 1}.

Sotto queste condizioni possiamo determinare le soluzioni parametriche:

\begin{align*} & x_{1,2} = \dfrac{6k \pm \sqrt{36k(k-1)}}{2 \cdot 1}=\dfrac{6k\pm 6\sqrt{k(k-1)}}{2}= \\ \\ & =\dfrac{\cancel{6}^3\left( k \pm \sqrt{k(k-1)}\right)}{\cancel{2}}= 3 \left( k \pm \sqrt{k^2-k}\right)\\ \\ & \text{con}\quad k \leq 0 \quad \vee  \quad  k \geq 1\end{align*}

Invece per {0<k<1} il discriminante è negativo e di conseguenza l’equazione è impossibile.

Esercizio 8

Proseguiamo gli esercizi sulle equazioni di secondo grado parametriche (letterali) con il seguente:

4x^2+4(k+3)x+6k+9+k^2=0

L’equazione è già in forma normale, con {a=4, \: b=4(k+3), \: c=6k+9+k^2}. Calcoliamo il discriminante:

\begin{align*} & \Delta=b^2-4ac=[4(k+3)]^2-4 \cdot 4 \cdot (\overbrace{6k+9+k^2}^{(k+3)^2})= \\ \\ & =16(k+3)^2-16(k+3)^2=0 \end{align*}

Il discriminante è nullo per cui per ogni valore di {k} avremo due soluzioni reali e coincidenti:

x_{1,2} = \dfrac{-b \pm \sqrt{\Delta}}{2a}=\dfrac{-4(k+3) \pm 0}{2 \cdot 4}=-\dfrac{1}{2}(k+3), \quad k \in \mathbb{R}

Terza parte: esercizi di livello avanzato (anche con più parametri)

Esercizio 9

Discutere al variare dei parametri le soluzioni della seguente equazione parametrica:

x^2+(2b-a)x-2ab=0

Dato che i parametri sono espressi con le lettere {a} e {b}, per non fare confusione utilizziamo per l’espressione del discriminante e per la formula risolutiva delle lettere maiuscole.

Cominciamo scrivendo il discriminante:

\begin{align*} & \Delta=B^2-4AC=(2b-a)^2-4 \cdot 1 \cdot (-2ab)=\\ \\ & = (2b-a)^2+8ab= 4b^2-4ab+a^2+8ab=\\ \\ & =a^2+4ab+4b^2=(a+2b)^2\end{align*}

Il determinante è un quadrato e quindi sarà sempre maggiore di zero o al più nullo. In particolare, il determinante è nullo per {a=0} e contemporaneamente {b=0}. In questa circostanza l’equazione ammetterà due soluzioni reali e coincidenti.

In generale avremo due soluzioni reali e distinte per ogni valore reale non nullo dei parametri {a} e {b}.

Calcoliamo le soluzioni parametriche dell’equazione:

\begin{align*} & x_{1,2} =\dfrac{-B \pm \sqrt{\Delta}}{2A}= \dfrac{-2b+a \pm \sqrt{(a+2b)^2}}{2 \cdot 1} = \dfrac{-2b+a \pm |a+2b|}{2} =  \\ \\ & =\begin{cases} \dfrac{-\cancel{2b}+a+a+\cancel{2b}}{2}=a \\ \\ \dfrac{-2b+\cancel{a}-\cancel{a}-2b}2{=-2b}\end{cases}  \\ \\ &\text{con} \quad a,\:b \in \mathbb{R}\end{align*}

Esercizio 10

Risolvere:

x^2+(3a-2b-1)x-6ab+2b=0

Calcoliamo il determinante:

\begin{align*} & \Delta =B^2-4AC = (3a-2b-1)^2-4 \cdot 1 \cdot (-6ab+2b)=\\ \\ & =9a^2+4b^2+1-12ab-6a+4b+24ab-8b=\\ \\ & =9a^2+4b^2+1+12ab-6a-4b=\\ \\ & =(3a+2b-1)^2 \end{align*}

Osserviamo che per i calcoli relativi al discriminante abbiamo ragionato con il quadrato di un trinomio.

Poiché il determinante è un quadrato le seguenti soluzioni parametriche saranno valide per ogni valore reale dei parametri:

\begin{align*} &x_{1,2} =\dfrac{-B \pm \sqrt{\Delta}}{2A}=\dfrac{-3a+2b+1 \pm \sqrt{(3a+2b-1)^2}}{2 \cdot 1} = \\ \\ & = \dfrac{-3a+2b+1\pm |3a+2b-1|}{2}= \\ \\ & =\begin{cases} \dfrac{-\cancel{3a}+2b+\cancel{1}+\cancel{3a}+2b-\cancel{1}}{2}=2b \\ \\ \dfrac{{-3a}+\cancel{2b}+1-{3a}-\cancel{2b}+1}{2}=\dfrac{2-6a}{2}=1-3a \end{cases} \\ \\ &\text{con} \quad a, \: b \: \in \mathbb{R}\end{align*} 

Esercizio 11

Proseguiamo gli esercizi sulle equazioni di secondo grado parametriche (letterali) con il seguente:

2kx^2+(1-2k^2)x-k=0

Calcoliamo il discriminante:

\begin{align*} & \Delta =  b^2-4ac=(1-2k^2)^2-4 \cdot (2k) \cdot (-k) = \\ \\ & =1-4k^2+4k^4+8k^2=1+4k^2+4k^4=(1+2k^2)^2\end{align*}

Il discriminante è un quadrato, quindi è maggiore o uguale a zero per ogni valore reale di {k}. Così otteniamo le soluzioni parametriche:

\begin{align*} & x_{1,2} = \dfrac{-b \pm \sqrt{\Delta}}{2a}=\dfrac{-1+2k^2 \pm \sqrt{(1+2k^2)^2}}{2 \cdot 2k}=  \\ \\ & =\dfrac{-1+2k^2 \pm |1+2k^2|}{4k}= \\ \\ & =\begin{cases} \dfrac{-1+2k^2+1+2k^2}{4k}=\dfrac{4k^2}{4k}=k, \quad k \neq 0 \\ \\ \dfrac{-1+2k^2-1-2k^2}{4k}=\dfrac{-2}{4k}=-\dfrac{1}{2k}, \quad k \neq 0\end{cases} \end{align*}

Le soluzioni hanno senso per ogni {k} reale tranne per {k=0}. Infatti, è presente un fattore {k} al denominatore nelle espressioni delle soluzioni non semplificate. E dobbiamo mantenere la condizione {k \neq 0 } anche per la soluzione {x_1 = k}, anche se in essa il parametro non compare a denominatore. Infatti, come sappiamo dalle frazioni algebriche, nel semplificare una frazione algebrica dobbiamo porre delle condizioni in modo da non alterare il campo di esistenza.

Per concludere l’esercizio, vediamo cosa succede per {k = 0}. L’equazione iniziale si riduce a:

2 \cdot 0 x^2 +(1-2 \cdot 0 ^2)x-0=0 \quad \Rightarrow \quad x = 0

Attenzione: in questo caso otteniamo un’unica soluzione e non due soluzioni uguali e coincidenti. Infatti, per {k=0} l’equazione di partenza si riduce ad una equazione di primo grado.

Esercizio 12

Risolvere:

x^2-2\sqrt{k}x-4=0

Osserviamo che l’equazione ha significato soltanto se vale la condizione di realtà del radicale {\sqrt{k}}. Dovremo quindi avere anzitutto la condizione:

k \geq 0

Infatti se {k < 0 } il coefficiente {b=-2\sqrt{k}} non ha significato.

A questo punto calcoliamo il discriminante:

\Delta=b^2-4ac=(-2\sqrt{k})^2-4 \cdot 1 \cdot (-4)=4k+16

Il discriminante sarà maggiore o uguale a zero per:

4k+16 \geq 0 \quad \Rightarrow \quad k \geq -\dfrac{16}{4}=-4

Tuttavia osserviamo che dovendo anche essere {k \geq 0} potremo considerare soltanto per il parametro {k} l’intervallo di valori corrispondenti a {k \geq 0}.

Sotto tale ipotesi abbiamo le soluzioni parametriche:

\begin{align*} & x_{1,2} = \dfrac{2\sqrt{k} \pm \sqrt{4k+16}}{2 \cdot 1}= \dfrac{2\sqrt{k} \pm \sqrt{4(k+4)}}{2}= \dfrac{2\sqrt{k} \pm 2 \sqrt{k+4}}{2}= \\ \\ & =\dfrac{2(\sqrt{k}\pm \sqrt{k+4})}{2}=\sqrt{k} \pm \sqrt{k+4}, \qquad \text{con} \quad k \geq 0\end{align*}

Esercizio 13

Vediamo come risolvere la seguente equazione di secondo grado parametrica:

kx^2-(k^2-k-2)x-2(k-1)=0

Calcoliamo il discriminante (come in un precedente esercizio dobbiamo ragionare con il quadrato di un trinomio):

\begin{align*} &\Delta = b^2-4ac=[-(k^2-k-2)]^2-4 \cdot k \cdot [-2(k-1)] = \\ \\ & =k^4+k^2+4-2k^3-4k^2+4k-4k(-2k+2)=\\ \\ & =k^4-3k^2+4-2k^3+4k+8k^2-8k=\\ \\ & =k^4+5k^2-2k^3-4k+4 = \\ \\ & =k^4+\overbrace{4k^2+k^2}^{5k^2}-2k^3-4k+4=\\ \\ & =(k^2+2-k)^2\end{align*}

Dato che il discriminante è non negativo per ogni {k}, otteniamo per ogni valore reale di {k} le seguenti soluzioni parametriche:

\small \begin{align*} & x_{1,2} = \dfrac{-b \pm \sqrt{\Delta}}{2a}=\dfrac{k^2-k-2 \pm \sqrt{(k^2+2-k)^2}}{2 \cdot k}=\\ \\ & = \dfrac{k^2-k-2 \pm |k^2+2-k|}{2k}= \\ \\ & =\begin{cases} 
 \dfrac{k^2-k-\cancel{2}+k^2+\cancel{2}-k}{2k} =\dfrac{2k^2-2k}{2k}=k-1, \quad  k \neq 0 \\ \\ \dfrac{\cancel{k^2}-\cancel{k}-2-\cancel{k^2}-2+\cancel{k}}{2k}=-\dfrac{2}{k}, \quad k \neq 0 \end{cases}\end{align*}

Invece per {k= 0 } l’equazione di partenza diviene:

0x^2-(0^2-0-2)x-2(0-1)=0 

e quindi (attenzione ai segni):

2x+2=0 \quad \Rightarrow \quad x=-1, \quad \text{con} \quad k = 0

La soluzione per {k=0} è unica poiché per tale valore del parametro l’equazione data si riduce ad un’equazione di primo grado.

Esercizio 14

Concludiamo questa serie di esercizi sulle equazioni di secondo grado parametriche (letterali) con il seguente:

(a+3)x^2+(2a+3)x-6=0

Calcoliamo il discriminante:

\begin{align*} &\Delta = B^2-4AC= (2a+3)^2-4 \cdot (a+3) \cdot (-6) = \\ \\ & =4a^2+12a+9+24a+72= \\ \\ & =4a^2+36a+81=(2a+9)^2\end{align*}

Dato che il discriminante è positivo per ogni valore reale del parametro, abbiamo:

\small \begin{align*} & x_{1,2} = \dfrac{-b \pm \sqrt{\Delta}}{2a}=\dfrac{-2a-3 \pm \sqrt{(2a+9)^2}}{2(a+3)}= \\ \\ & =\dfrac{-2a-3\pm|2a+9|}{2(a+3)} =\begin{cases}\dfrac{-\cancel{2a}-3+\cancel{2a}+9}{2(a+3)}=\dfrac{3}{a+3}, \quad a \neq -3\\ \\ \dfrac{-2a-3-2a-9}{2(a+3)} =\dfrac{-4a-12}{2(a+3)}=-2, \quad a \neq -3\end{cases}\end{align*}

La condizione {a \neq -3 } è necessaria per evitare che si annulli il denominatore nelle espressioni delle soluzioni.

Invece per {a=-3} l’equazione di partenza diviene:

-3x-6=0 \quad \Rightarrow x=-2, \qquad \text{con} \quad a = -3

ed abbiamo un’unica soluzione poiché per tale valore del parametro l’equazione diventa di primo grado.

Per quanto riguarda gli esercizi sulle equazioni di secondo grado parametriche (letterali) è tutto. Buon proseguimento!