Differenza tra insiemi

 - 

Insiemi

La differenza tra i due insiemi A e B è l’insieme A – B degli elementi che appartengono all’insieme A ed allo stesso tempo non appartengono all’insieme B. In altre parole, l’insieme differenza A – B è dato dall’insieme A privato degli elementi in comune con l’insieme B.

Introduciamo così in questa lezione la differenza tra insiemi, che è la terza operazione di questa serie di lezioni, e che si affianca alla unione e alla intersezione tra insiemi. Osserviamo che la differenza tra insiemi, in quanto operazione insiemistica, presenta delle caratteristiche diverse rispetto alla sottrazione tra numeri. Ad esempio, se sottraiamo ad un insieme A un insieme B anche non vuoto che non ha alcun elemento in comune con l’insieme A, il risultato che otteniamo è ancora l’insieme A. Siamo cioè nel caso in cui gli insiemi {A} e {B} sono disgiunti. Questa è una differenza peculiare rispetto alla sottrazione tra numeri. Infatti, se sottraiamo un numero a ad un numero b diverso da zero, il risultato che otterremo sarà sempre una quantità diversa da a.

Vediamo allora nel dettaglio l’operazione insiemistica di differenza tra insiemi, fornendone la definizione anche con l’uso di simboli, le proprietà e degli esempi.

Differenza tra insiemi: definizione

Dati due insiemi {A} e {B} e fissato per essi un insieme universo {E}, la differenza tra i due insiemi {A - B} (indicata anche con {A \setminus B}) è data da un insieme che contiene gli elementi dell’insieme {A} tali da non appartenere all’insieme {\textbf{B}}. In simboli:{A - B = \{x \in E | x \in A \: \wedge \: x \not \in B\}}

Ricordiamo che il simbolo “{\wedge}” significa “e contemporaneamente”.

Ora, anticipando la definizione di insieme complementare, è possibile esprimere la differenza {A - B} nella seguente forma alternativa:

A - B = A \cap \mathcal{C}_{E}B

Con il simbolo {\mathcal{C}_E B} intendiamo l’insieme complementare di {B}, ovvero tutti gli elementi dell’insieme universo {E} tali da non appartenere all’insieme {B}. Così, con l’operazione {A \cap \mathcal{C}_{E}B} quello che facciamo è costruire un insieme costituito dagli elementi dell’insieme complementare di {B} (escludendo in questo modo gli elementi dell’insieme {B}) tali da appartenere all’insieme {A}. Ed in tal modo otteniamo lo stesso insieme differenza {A - B}.

Esempi sulla differenza tra insiemi

Esempio 1

Fissato un universo {E}, l’insieme differenza tra i due insiemi:

A=\left\{9,8,7 \right\}, \qquad B=\left\{ 1,3,7\right\}

è dato da:

A-B = \left\{ x \in  E \: | \: x \in A \: \wedge x \not \in B\right\}

ovvero rappresentandolo per elencazione:

A- B = \left\{ 9,8\right\}

Infatti {9} e {8} sono gli elementi dell’insieme {A} che non appartengono all’insieme {\textbf{B}}. L’elemento {7} appartiene invece ad entrambi gli insiemi {A} e {B} e di conseguenza non è contenuto nell’insieme differenza. Infine, gli elementi {1} e {3} dell’insieme {B} non hanno alcun effetto sull’operazione.

Esempio 2

Fissato un universo {E} consideriamo i due insiemi:

A=\{5, 6, 7, 10 \}, \qquad B=\left\{ 1,3,7,10\right\}

L’insieme differenza è dato da:

A - B = \left\{ 5, 6\right\}

Questi infatti sono gli elementi dell’insieme {A} che non appartengono all’insieme {B}.

Ora, vediamo di utilizzare la definizione alternativa della differenza insiemistica che fa uso dell’insieme complementare. In questo modo il calcolo è più lungo, ma il nostro obiettivo qui è testare tale definizione.

Prendiamo allora per gli insiemi {A} e {B} dati come insieme universo l’insieme:

E=\left\{ x \in \N \: | \: x < 11\right\}

ovvero:

E= \left\{ 0, 1,2,3,4,5,6,7,8,9,10\right\}

Osserviamo che un tale insieme è accettabile come universo per gli insiemi {A} e {B} in quanto è un sovrainsieme per entrambi. Detta in altri termini, sia {A}, sia {B} sono dei sottoinsiemi di {E}.

Determiniamo ora l’insieme complementare di {B} rispetto al fissato universo {E}. Basta semplicemente togliere all’insieme universo {E} gli elementi dell’insieme {B=\left\{ 1,3,7,10\right\}}:

\mathcal{C}_E B = \left\{ 0,2,4,5,6,8,9\right\}

Calcoliamo a questo punto la differenza {A - B}, come:

\begin{align*} & A - B = A \cap \mathcal{C}_E B=\left\{ 5,6,7,10\right\} \cap \left\{ 0,2,4,5,6,8,9\right\}= \\ \\ & = \left\{ 5, 6\right\}\end{align*}

Effettivamente abbiamo ottenuto lo stesso risultato del procedimento precedente.

La differenza tra insiemi non è commutativa

Osserviamo che è fondamentale l’ordine con il quale si effettua la differenza tra insiemi. In altre parole, l’insieme differenza:

A - B

è diverso dall’insieme differenza:

B - A

Quindi:

A - B \neq B - A 

Facendo degli esempi sulla non commutatività della differenza tra insiemi, considerando ad esempio i due insiemi:

A=\{1,5,9\}, \qquad B = \left\{ 1,7,9\right\}

abbiamo:

A - B = \left\{ 5\right\}, \qquad B-A=\left\{ 7\right\}

Ancora, dati gli insiemi:

A=\{x \in \N \: | \: x < 5\}, \qquad B=\left\{ x \in \N | x > 2\right\}

ovvero:

A=\left\{ 0,1,2,3,4\right\}, \qquad B = \left\{ 3,4,5,\dots\right\}

abbiamo:

A- B = \left\{ 0,1,2\right\}, \qquad B-A=\left\{5,\dots\right\}

Addirittura nel primo caso otteniamo un insieme finito, mentre nel secondo caso otteniamo un insieme infinito.

Quindi, ricordiamo: la differenza insiemistica non è commutativa.

Differenza tra insiemi e diagrammi di Venn

Possiamo rappresentare la differenza {A - B} tra due insiemi {A} e {B} in un fissato universo {E} mediante i diagrammi di Venn:

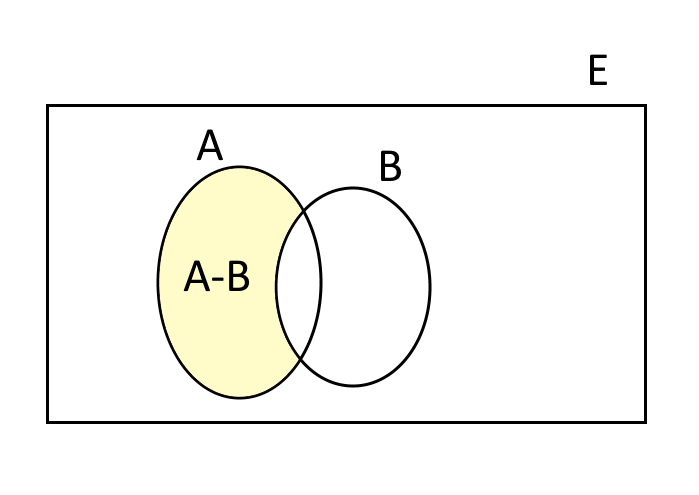
L’insieme differenza è rappresentato nel colore giallo.

Proprietà della differenza tra insiemi

Vediamo alcune ulteriori proprietà che caratterizzano l’operazione insiemistica di differenza insiemistica.

Differenza tra insiemi e insieme vuoto

Abbiamo:

A- \emptyset = A; \qquad \emptyset-A=\emptyset

Effettivamente se sottraiamo ad un insieme {A} l’insieme vuoto ritroviamo l’insieme {A}, poiché l’insieme {A} non potrà mai avere alcun elemento che appartiene all’insieme vuoto. Quindi non dobbiamo privare l’insieme {A} di alcun elemento.

Viceversa, se sottraiamo all’insieme vuoto un insieme {A} otteniamo come risultato l’insieme vuoto. Infatti, siamo nel caso della differenza tra due insiemi disgiunti (ovvero, con intersezione uguale all’insieme vuoto).

Differenza tra un insieme e sé stesso

Se sottraiamo un insieme con sé stesso dobbiamo privarlo di tutti i suoi elementi, e quindi otteniamo come risultato l’insieme vuoto.

A - A = \emptyset 

Differenza tra un insieme e un suo sovrainsieme

Se {A \supseteq B}, ovvero {A} è un sovrainsieme di {B}, allora per la differenza tra l’insieme {B} e il suo sovrainsieme {A} abbiamo:

B-A=\emptyset

Differenza tra insiemi e relazione di inclusione

Si ha, considerati due insiemi {A} e {B} qualsiasi:

A - B \subseteq A, \qquad B-A \subseteq B

In altre parole l’insieme differenza è sempre un sottoinsieme dell’insieme “minuendo” (il primo insieme).

Insiemi disgiunti

Se i due insiemi {A} e {B} sono disgiunti, ovvero se:

A \cap B = \emptyset

allora per la differenza tra i due insiemi abbiamo:

A - B = A; \qquad B-A = B

In altre parole, se i due insiemi {A} e {B} sono disgiunti il risultato della differenza tra i due insiemi è uguale al primo insieme che figura nell’operazione (insieme “minuendo”).

Conclusioni

Per questa lezione sulla differenza tra insiemi è tutto. Abbiamo presentato la definizione dell’operazione ed esposto le sue principali proprietà. Ed abbiamo tra l’altro visto la relazione che esiste tra questa operazione e l’intersezione tra insiemi.

Nella prossima lezione vedremo nel dettaglio la definizione di insieme complementare. E metteremo in relazione la differenza insiemistica proprio con la definizione di insieme complementare, evidenziando ulteriori proprietà.

Buon proseguimento con SìMatematica! 🙂