Prodotto cartesiano

 - 

Insiemi

Il prodotto cartesiano di due insiemi A e B è per definizione l’insieme di tutte le possibili coppie ordinate (a,b), ove a è elemento dell’insieme A e b è elemento dell’insieme B. Le coppie sono ordinate e di conseguenza il prodotto cartesiano degli insiemi A e B sarà dato da tutte le possibili coppie (a,b), mentre il prodotto cartesiano degli insiemi B e A sarà invece dato da tutte le possibili coppie (b,a). Così il prodotto cartesiano non dispone della proprietà commutativa. Ma vedremo tutti i dettagli tra un instante.

In questa lezione conclusiva sugli insiemi vediamo dunque la definizione di prodotto cartesiano tra due insiemi {A} e {B}, proponendo esempi e le modalità di rappresentazione grafica per tale operazione.

Numerose sono le applicazioni della definizione di prodotto cartesiano. Consideriamo ad esempio un sistema di riferimento dato dagli assi cartesiani {x} e {y}. Per ogni asse è possibile associare a ciascun punto di esso un numero reale. In altre parole, possiamo stabilire una corrispondenza tra ogni asse cartesiano e l’insieme dei numeri reali {\R}. Ora, grazie ad un sistema di riferimento cartesiano di questo tipo è possibile associare ad ogni punto del piano una coppia {(x,y)}. E come vedremo, tutte le possibili coppie {(x,y)} appartengono all’insieme dato dal prodotto cartesiano dell’insieme {\R} con sé stesso (in simboli, {\R \times \R }).

Allo stesso modo, se consideriamo un sistema di riferimento cartesiano dato dai tre assi {x,y,z}, è possibile associare a ciascun punto dello spazio una terna {(x,y,z)}. E tutte le possibili terne {(x,y,z)} appartengono all’insieme che si ottiene dal prodotto cartesiano {\R \times \R \times \R}.

Definizione di prodotto cartesiano

Introduciamo subito la definizione rigorosa di prodotto cartesiano.

Dati due insiemi {A} e {B}, definiamo come prodotto cartesiano {A \times B} dei due insiemi {A} e {B} l’insieme di tutte le coppie ordinate {(a,b)}, con {a \in A} e {b \in B}. In simboli:{A \times B = \left\{ (a,b) \: | \: a \in A \: \wedge \: b \in B\right\}}

Così indichiamo il prodotto cartesiano tra due insiemi {A} e {B} utilizzando l’espressione {A \times B}, nella quale compare lo stesso simbolo che si utilizza nella moltiplicazione in aritmetica. E l’espressione {A \times B} si legge “A cartesiano B” oppure più semplicemente “A per B”. Gli insiemi {A} e {B} sono i fattori del prodotto cartesiano. Ed in ciascuna coppia ordinata {(a,b)}, la quantità {a} si chiama prima coordinata, mentre la quantità {b} si chiama seconda coordinata.

Esempi sul prodotto cartesiano

Consideriamo i due insiemi finiti:

A=\left\{ 1,2,3\right\}, \qquad B=\left\{ 5,6\right\}

Il prodotto cartesiano del primo insieme per il secondo insieme è dato da tutte le possibili coppie ordinate del tipo {(a,b)}:

A \times  B = \left\{(1,5),(1,6),(2,5),(2,6),(3,5),(3,6)\right\}

L’insieme “prodotto cartesiano” {A \times B} contiene tutte le possibili coppie ordinate {(a,b)} che è possibile costruire a partire dagli insiemi {A} e {B}. E attenzione, la prima coordinata di ciascuna coppia deve appartenere al primo fattore nel prodotto cartesiano, e la seconda coordinata al secondo fattore nel prodotto cartesiano. Così al prodotto cartesiano {A \times B} corrispondono coppie del tipo {(a,b)} e non {(b,a)}.

Ma, vi domanderete: dati due insiemi {A} e {B}, come è possibile scrivere con sicurezza tutte le possibili coppie {(a,b)}? Ora, per la determinazione di tutte le coppie {(a,b)} basta seguire una semplice regola.

In particolare, per calcolare il prodotto cartesiano {A \times B}, cominciamo fissando un elemento dell’insieme {A}. Per “fissare un elemento” intendiamo considerare per il momento solo quel dato elemento.

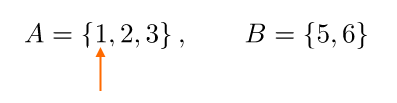
A questo punto consideriamo il fissato elemento dell’insieme {A} ed associamolo di volta in volta a ciascun elemento dell’insieme {B}. Per ciascuna associazione scriviamo una coppia di elementi {(a,b)}:

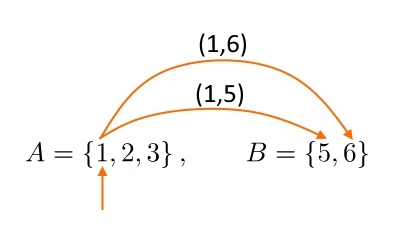
Così intanto per il prodotto cartesiano abbiamo determinato delle prime coppie ordinate {(a,b)}, ovvero:

 (1,5),(1,6)

Ora fissiamo il secondo elemento dell’insieme {A}:

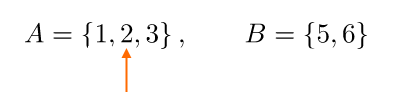
Come nel caso precedente, associamo l’elemento fissato dell’insieme {A} a ciascun elemento dell’insieme {B}:

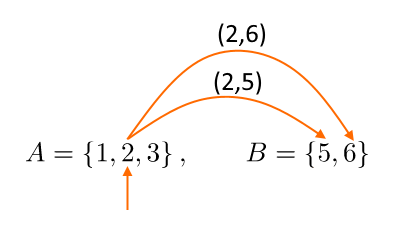
Così, nel prodotto cartesiano avremo anche le coppie:

(2,5),(2,6)

Ancora, non abbiamo terminato. Dobbiamo fissare il terzo elemento dell’insieme {A}:

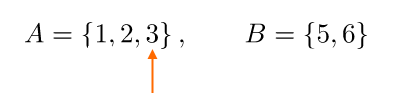
e quindi associare al terzo elemento dell’insieme {A} ciascuno degli elementi dell’insieme {B}:

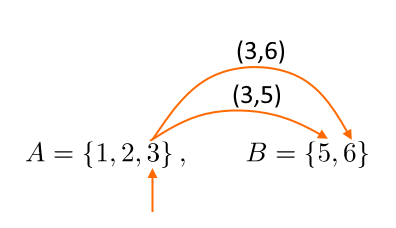
Abbiamo quindi anche le coppie:

(3,5),(3,6)

A questo punto abbiamo terminato, poiché abbiamo esaurito tutti gli elementi dell’insieme {A}. Mettendo insieme tutte le coppie {(a,b)} sin qui ottenute ritroviamo l’insieme {A \times B}:

A \times B= \left\{(1,5),(1,6),(2,5),(2,6),(3,5),(3,6))\right\}

Osservazione. Per il calcolo del prodotto {A \times B}, è anche possibile fissare di volta in volta un elemento dell’insieme {B} e costruire le coppie che si ottengono associando l’elemento fissato dell’insieme {B} a ciascun elemento dell’insieme {A}. Si procederà in questo modo fino ad esaurire gli elementi dell’insieme {B}. Utilizzando questa regola alternativa si ottiene comunque lo stesso risultato, anche se le coppie vengono elencate in un ordine diverso. Come sappiamo, infatti, nell’elencare gli elementi di un insieme l’ordine non conta.

Proviamo ora a calcolare con le regole stabilite l’insieme {B \times A}, sempre considerando gli stessi insiemi {A} e {B}. Riportiamo di nuovo per comodità le rappresentazioni tabulari dei due insiemi:

 B=\left\{ 5,6\right\}, \qquad A=\left\{ 1,2,3\right\}

Abbiamo:

B \times A = \left\{ (5,1),(5,2),(5,3),(6,1),(6,2),(6,3)\right\}

Confrontando i due insiemi ottenuti è immediato verificare che:

A \times B \neq B \times A

ove il simbolo “{\neq}” significa diverso. Infatti, siccome stiamo lavorando con coppie ordinate, abbiamo che ad esempio la coppia {(1,5)} è diversa dalla coppia {(5,1)}, pur essendo formata ciascuna dagli stessi numeri. Di conseguenza, il prodotto cartesiano non dispone della proprietà commutativa, ovvero non è commutativo. Questa è un’importante differenza rispetto al prodotto tra numeri.

Proprietà del prodotto cartesiano

Elenchiamo ora le principali proprietà del prodotto cartesiano, mettendolo in relazione ai concetti di insieme vuoto, alle operazioni insiemistiche di unione ed intersezione ed infine alla cardinalità degli insiemi.

1) Insieme vuoto

Se uno dei due fattori del prodotto cartesiano è l’insieme vuoto, abbiamo:

A \times \emptyset = \emptyset; \qquad \emptyset \times A = \emptyset 

In entrambi i casi non è possibile costruire nessuna coppia. Infatti, poiché uno dei fattori è l’insieme vuoto, nel tentare di costruire le coppie ci ritroviamo con una coordinata mancante. Di conseguenza, non potendo costruire alcuna coppia, il risultato del prodotto è un insieme privo di elementi, quindi l’insieme vuoto.

2) Proprietà distributiva rispetto all’unione

Si ha:

A \times (B \cup C) =( A \times B )\cup (A \times C)

3) Proprietà distributiva rispetto all’intersezione

Abbiamo:

A \times (B \cap C) = (A \times B) \cap (A \times C)

4) Cardinalità dell’insieme prodotto cartesiano

Dati due insiemi finiti {A} e {B}, con rispettivamente {\text{card}(A)=n, \: \text{card}(B)=m, \: n, m \in \N}, abbiamo:

\small \text{card}(A \times B)=n \cdot m

In parole semplici, se consideriamo insiemi finiti, il numero di coppie che si ottengono è dato dal prodotto del numero di elementi del primo insieme per il numero di elementi del secondo insieme.

Questa regola è molto importante poiché consente di verificare se abbiamo scritto tutte le coppie.

Ad esempio, dati gli insiemi:

A=\left\{ 1,2,3\right\}, \qquad B=\left\{ 5,6\right\}

abbiamo:

\text{card}(A)=3, \qquad \text{card}(B)=2

e quindi:

\text{card}(A) \cdot \text{card}(B)=3\cdot2=6=\text{card}(A \times B)

Effettivamente l’insieme {A \times B} come visto negli esempi precedenti è il seguente:

A \times  B = \left\{(1,5),(1,6),(2,5),(2,6),(3,5),(3,6)\right\}

ed è proprio costituito da 6 coppie.

Come rappresentare il prodotto cartesiano

Vediamo ora le varie modalità con le quali è possibile rappresentare graficamente il prodotto cartesiano. Consideriamo negli esempi a seguire i due insiemi:

A = \left\{ 2,4\right\}, \qquad B=\left\{ 3,5\right\}

Applicando le regole sin qui viste abbiamo:

A \times B = \left\{ (2,3), (2,5), (4,3),(4,5)\right\}

Diagrammi di Venn

E’ possibile rappresentare l’insieme {A \times B} mediante i diagrammi di Venn, riportando all’interno dell’ovale corrispondente all’insieme {A \times B} ciascuna coppia:

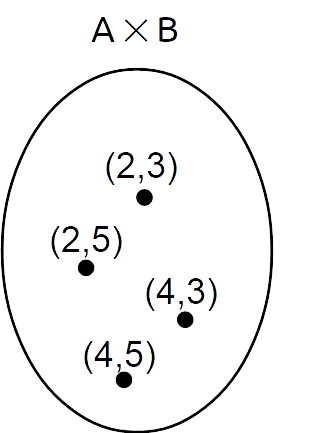
Tabella a doppia entrata

Utilizzando una tabella a doppia entrata è possibile aiutarsi nella determinazione delle coppie:

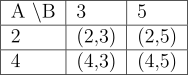
Infatti, costruendo la tabella sapremo che avremo scritto tutte le coppie quando avremo riempito tutte le caselle vuote corrispondenti alle coppie stesse.

Nella prima colonna a sinistra e nella prima riga in alto vengono riportati gli elementi di ciascun insieme, mentre nelle rimanenti celle della tabella vengono riportare le coppie. Osserviamo che ciascuna coppia si ottiene per incrocio di una certa riga e di una certa colonna.

La rappresentazione mediante tabella a doppia entrata suggerisce un altro tipo di rappresentazione, che è quella mediante l’utilizzo di un diagramma cartesiano.

Rappresentazione mediante diagramma cartesiano

Consideriamo un diagramma cartesiano, e riportiamo nell’asse {x} gli elementi dell’insieme {A}, nell’asse {y} gli elementi dell’insieme {B}. A ciascuna coppia associamo un punto nel piano cartesiano avente per ascissa un elemento dell’insieme {A} e per ordinata un elemento dell’insieme {B}. Indichiamo inoltre l’asse {x} con il nome dell’insieme {A} e l’asse {y} con il nome dell’insieme {B}:

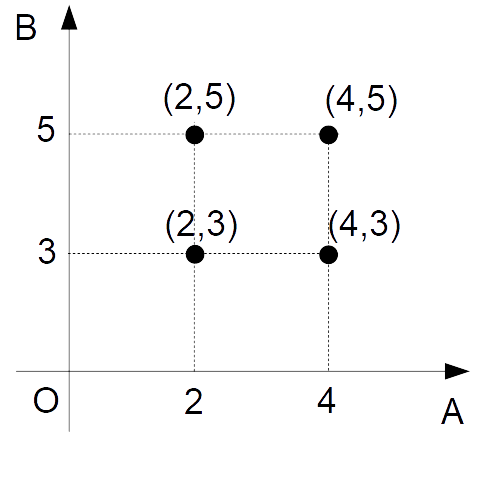
Ulteriori rappresentazioni degli insiemi sono date dai diagrammi ad albero e dalla rappresentazione sagittale, ma per brevità di queste non ci occuperemo.

Conclusioni

Per quanto riguarda questa lezione è tutto. Qui si conclude anche il ciclo di lezioni sugli insiemi di SìMatematica. In questo corso abbiamo dato un approfondito sguardo alla teoria degli insiemi per quanto riguarda gli studenti delle scuole medie e superiori. Un saluto a tutti voi!