Espressioni con frazioni algebriche

 - 

Frazioni algebriche

In questa lezione mettiamo in pratica tutto quanto visto sulle operazioni con le frazioni algebriche presentando degli esercizi sulle espressioni con frazioni algebriche, svolti e commentati. Negli esercizi incontreremo le principali operazioni sulle frazioni algebriche che abbiamo trattato nella lezione teorica: somma algebrica, moltiplicazione e divisione. Per espressioni contenenti anche le potenze è disponibile un’ulteriore esercitazione.

Negli esercizi sulle espressioni con frazioni algebriche presenti in questa lezione tratteremo in modo approfondito anche il teorema di Ruffini e le sue applicazioni. Grazie al teorema riusciremo in particolare in alcuni casi a scomporre più rapidamente i polinomi presenti nell’espressione, evitando lunghe scomposizioni.

Per il calcolo delle espressioni con frazioni algebriche dovremo utilizzare le stesse regole di precedenza valide per le espressioni numeriche. Ricordiamo che in assenza di parentesi o comunque all’interno delle parentesi:

• le potenze hanno la precedenza su tutte le altre operazioni;
• le moltiplicazioni e le divisioni hanno la precedenza sulle addizioni e le sottrazioni;
• in presenza di sole moltiplicazioni e divisioni le operazioni si eseguono nell’ordine da sinistra verso destra.

Per quanto riguarda le parentesi, bisogna eseguire prima i calcoli all’interno delle parentesi tonde, poi quelli all’interno delle parentesi quadre e infine i calcoli all’interno delle parentesi graffe. Ricordate queste semplici regole, per il resto basterà applicare quanto sappiamo sulle operazioni con le frazioni algebriche e sulla scomposizione in fattori dei polinomi.

Precisiamo infine che l’obiettivo del calcolo delle espressioni con frazioni algebriche è quello di riscrivere l’espressione di partenza come un’unica frazione algebrica, semplificandola il più possibile.

Passiamo allora subito all’azione con gli esercizi sulle espressioni con frazioni algebriche.

Esercizi svolti sulle espressioni con frazioni algebriche

Esercizio 1

Calcolare la seguente espressione con frazioni algebriche:

\left( \dfrac{a+b}{a-b}-\dfrac{a-b}{a+b}\right):\dfrac{2ab}{a^2-b^2}

Cominciamo sommando algebricamente tra loro le frazioni all’interno delle parentesi tonde:

\begin{align*} &\left( \dfrac{a+b}{a-b}-\dfrac{a-b}{a+b}\right):\dfrac{2ab}{a^2-b^2} = \\ \\ & = \dfrac{(a+b)(a+b)-(a-b)(a-b)}{(a-b)(a+b)}: \dfrac{2ab}{a^2-b^2}=\end{align*}

A questo punto scomponiamo il denominatore della frazione al divisore (differenza di quadrati):

=\dfrac{(a+b)(a+b)-(a-b)(a-b)}{(a-b)(a+b)}: \dfrac{2ab}{(a+b)(a-b)}=

Ora dobbiamo eseguire una divisione tra frazioni algebriche. Ricordiamo la regola: dobbiamo sostituire l’operatore di divisione con quello di moltiplicazione, scambiando allo stesso tempo tra loro il numeratore e il denominatore della frazione algebrica al divisore:

=\dfrac{(a+b)(a+b)-(a-b)(a-b)}{(a-b)(a+b)} \cdot \dfrac{(a+b)(a-b)}{2ab}=

Ci siamo in questo modo ricondotti ad una moltiplicazione tra frazioni algebriche. Eseguiamo le semplificazioni incrociate, stando attenti a rispettare la proprietà invariantiva della divisione. In pratica possiamo semplificare soltanto i fattori al denominatore della prima frazione con i fattori al numeratore della seconda frazione, ove abbiamo soltanto prodotti:

\begin{align*} & =\dfrac{(a+b)(a+b)-(a-b)(a-b)}{\cancel{(a-b)}\cancel{(a+b)}} \cdot \dfrac{\cancel{(a+b)}\cancel{(a-b)}}{2ab}=  \\ \\ & =\dfrac{(a+b)(a+b)-(a-b)(a-b)}{2ab}=\end{align*}

Dato che a questo punto non abbiamo altre semplificazioni da fare conviene riscrivere il numeratore sfruttando la proprietà del prodotto tra potenze di uguale base:

=\dfrac{(a+b)^2-(a-b)^2}{2ab}=

E’ ora possibile riconoscere al numeratore una differenza tra quadrati {A^2-B^2} ponendo {A=a+b} e {B=a-b}. Si ha:

\begin{align*}=&\dfrac{(\overbrace{a+b+a-b}^{A+B})(\overbrace{a+b-(a-b)}^{A-B})}{2ab}= \dfrac{(a+\cancel{b}+a-\cancel{b})(\cancel{a}+b-\cancel{a}+b)}{2ab}=\\ \\ & =\dfrac{\cancel{2}\cancel{a} \cdot 2\cancel{b}}{\cancel{2}\cancel{a}\cancel{b}}=2  &\end{align*}

Abbiamo così concluso il primo di questa serie di esercizi sulle espressioni con le frazioni algebriche.

Esercizio 2

Calcolare la seguente espressione con frazioni algebriche:

\left( \dfrac{x}{x+y}-\dfrac{x^2}{x^2+2xy+y^2}\right):\dfrac{x^2y^2}{x^3+y^3}

Scomponiamo in fattori i polinomi presenti nelle frazioni ove possibile. Per il denominatore {x^3+y^3} dovremo in particolare utilizzare la regola della scomposizione in fattori con la somma di cubi. Rimandiamo però tale scomposizione in un secondo tempo. Nel denominatore della seconda frazione all’interno delle parentesi tonde riconosciamo invece il quadrato di un binomio, che conviene invece scomporre subito.

E’ inoltre già possibile ricondurre la divisione presente nell’espressione ad una moltiplicazione, scambiando di posto tra loro il numeratore e il denominatore della frazione al divisore. Abbiamo:

\begin{align*} & \left( \dfrac{x}{x+y}-\dfrac{x^2}{x^2+2xy+y^2}\right):\dfrac{x^2y^2}{x^3+y^3} = \\ \\ & = \left[\dfrac{x}{x+y}-\dfrac{x^2}{(x+y)^2}\right] \cdot \dfrac{x^3+y^3}{x^2y^2} = \end{align*}

A questo punto sommiamo algebricamente tra loro le frazioni all’interno delle parentesi:

=\dfrac{(x+y)\cdot x-x^2}{(x+y)^2} \cdot \dfrac{x^3+y^3}{x^2y^2}=

Ora calcoliamo il prodotto al numeratore della prima frazione e scomponiamo il numeratore della seconda:

\begin{align*} & =\dfrac{\cancel{x^2}+xy-\cancel{x^2}}{(x+y)^2} \cdot \dfrac{(x+y)(x^2-xy+y^2)}{x^2y^2} = \\ \\ & =\dfrac{\cancel{x}\cancel{y}}{(x+y)^{\cancel{2}}} \cdot \dfrac{\cancel{(x+y)}(x^2-xy+y^2)}{x^{\cancel{2}}y^{\cancel{2}}} = \\ \\ & =\dfrac{x^2-xy+y^2}{(x+y) \cdot xy}= \dfrac{x^2-xy+y^2}{x^2y+xy^2}\end{align*}

Esercizio 3

Proseguiamo gli esercizi sulle espressioni con le frazioni algebriche con il seguente esercizio:

\left[ \dfrac{1}{a+1}-\dfrac{1}{a-1}-\dfrac{2a}{1-a^2}-\dfrac{2a}{(1+a)^2}\right]:\dfrac{4a^3}{1+a^3}

Osserviamo che non dobbiamo sviluppare il quadrato {(1+a)^2}, ma piuttosto rileggerlo come il prodotto {(1-a)(1-a)}. E’ inoltre opportuno scomporre il denominatore {1-a^2} della terza frazione come {(1+a)(1-a)}. Possiamo inoltre ricondurre fin da subito la divisione presente nell’espressione ad una moltiplicazione scambiando tra loro il numeratore e il denominatore della frazione al divisore.

\begin{align*} &\left[ \dfrac{1}{a+1}-\dfrac{1}{a-1}-\dfrac{2a}{1-a^2}-\dfrac{2a}{(1+a)^2}\right]:\dfrac{4a^3}{1+a^3}= \\ \\ & = \left[ \dfrac{1}{a+1}-\dfrac{1}{a-1}-\dfrac{2a}{(1+a)(1-a)}-\dfrac{2a}{(1+a)(1+a)}\right] \cdot \dfrac{1+a^3}{4a^3}=\end{align*}

Proseguiamo ora sommando algebricamente tra loro le frazioni algebriche all’interno delle parentesi. Prima conviene lavorare sui segni della seconda frazione, in modo da rendere più compatto il denominatore comune. In particolare, cambiamo il segno davanti alla linea di fratto e contemporaneamente invertiamo i segni di tutti i termini al denominatore. In tal modo ritroviamo un fattore {1-a}, presente anche nella terza frazione. Ciò consente di avere un fattore in meno nel denominatore comune.

\begin{align*} &= \left[ \dfrac{1}{a+1}\boxed{+\dfrac{1}{-a+1}}-\dfrac{2a}{(1+a)(1-a)}-\dfrac{2a}{(1+a)(1+a)}\right] \cdot \dfrac{1+a^3}{4a^3} = \\ \\ & =\dfrac{(1+a)(1-a)+(1+a)^2-(1+a)\cdot2a-(1-a)\cdot2a}{(1+a)^2(1-a)}  \cdot\dfrac{1+a^3}{4a^3}= \\ \\ & =\dfrac{1-a^2+1+2a+a^2-(2a+2a^2)-(2a-2a^2)}{(1+a)^2(1-a)} \cdot\dfrac{1+a^3}{4a^3}= \\ \\ & =\dfrac{1-\cancel{a^2}+{1}+\cancel{2a}+\cancel{a^2}-\cancel{2a}-\cancel{2a^2}-2a+\cancel{2a^2}}{(1+a)^2(1-a)}\cdot\dfrac{1+a^3}{4a^3}=\\ \\ & =\dfrac{2-2a}{(1+a)^2(1-a)} \cdot\dfrac{1+a^3}{4a^3}=\dfrac{2-2a}{(1+2a+a^2)(1-a)}\cdot\dfrac{1+a^3}{4a^3}=\\ \\ & =\dfrac{\cancel{2}(1-a)}{1-a+2a-2a^2+a^2-a^3} \cdot\dfrac{1+a^3}{\cancel{4}^{\scriptsize \displaystyle2}a^{3}}=\\ \\ & =\dfrac{1-a}{-a^3-a^2+a+1} \cdot\dfrac{1+a^3}{2a^3}= \quad (*)\end{align*}

Scomponiamo separatamente il polinomio al denominatore della prima frazione. Questo ha per radice il valore {c=1} (ovvero si annulla per {a=1}) ed è dunque divisibile per il binomio {a-c} ovvero {a-1}:

-a^3-a^2+a+1=(a-1)\cdot Q(a)

Il polinomio {Q(a)} sarà il quoziente tra il polinomio da scomporre e {a-1}. Eseguendo il calcolo con la regola di Ruffini otteniamo:

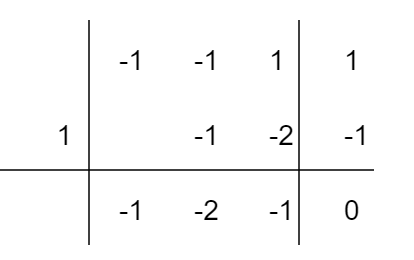
Q(a)=-a^2-2a-1=-(a^2+2a+1)=-(a+1)^2

Per cui vale in conclusione la scomposizione:

\begin{align*} & -a^3-a^2+a+1=(a-1)[-(a+1)^2]=\\ \\ & =(a-1) \cdot (-1) \cdot (a+1)^2=(1-a)(a+1)^2 \end{align*}

Quindi tornando all’espressione e proseguendo i passaggi:

(*) =  \dfrac{\cancel{1-a}}{\cancel{(1-a)}(a+1)^2} \cdot\dfrac{1+a^3}{2a^3}=\dfrac{1+a^3}{(a+1)^2\cdot2a^3}=

A questo punto scomponiamo il numeratore della seconda frazione algebrica utilizzando la regola della somma di cubi.

=\dfrac{\cancel{(1+a)}(1-a+a^2)}{(a+1)^{\cancel{2}}\cdot 2a^3}=\dfrac{1-a+a^2}{2a^3(a+1)}

e siamo arrivati.

Esercizio 4

Calcolare la seguente espressione con frazioni algebriche:

\dfrac{3a^2-7ab+4b^2}{2a^2-ab-6b^2}:\dfrac{(a^4-b^4)(3a-4b)}{(a^3-8b^3)(2a+3b)}

Cominciamo riscrivendo la divisione come una moltiplicazione:

\begin{align*} &\dfrac{3a^2-7ab+4b^2}{2a^2-ab-6b^2}:\dfrac{(a^4-b^4)(3a-4b)}{(a^3-8b^3)(2a+3b)}= \\ \\ & = \dfrac{3a^2-7ab+4b^2}{2a^2-ab-6b^2} \cdot\dfrac{(a^3-8b^3)(2a+3b)}{(a^4-b^4)(3a-4b)}\end{align*}

Vediamo se i polinomi al numeratore e al denominatore della prima frazione sono divisibili rispettivamente per i fattori {3a-4b} e {2a+3b} presenti nella seconda frazione. Proviamo ad eseguire direttamente le divisioni, ad esempio utilizzando la regola generale (in questo modo non dobbiamo ricercare le eventuali radici dei polinomi). In particolare per scomporre i polinomi dobbiamo ottenere resto zero in ciascuna divisione.

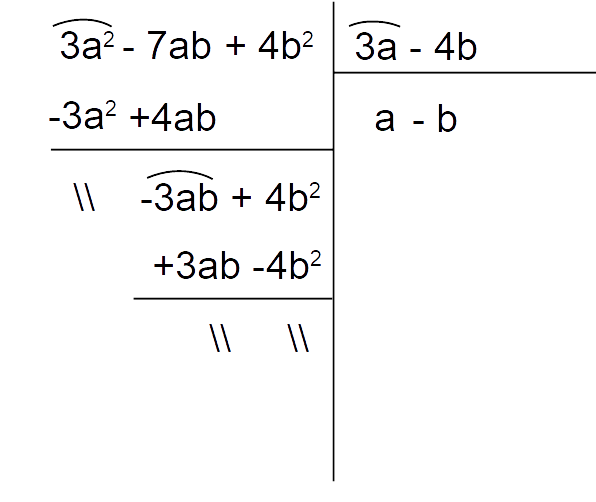
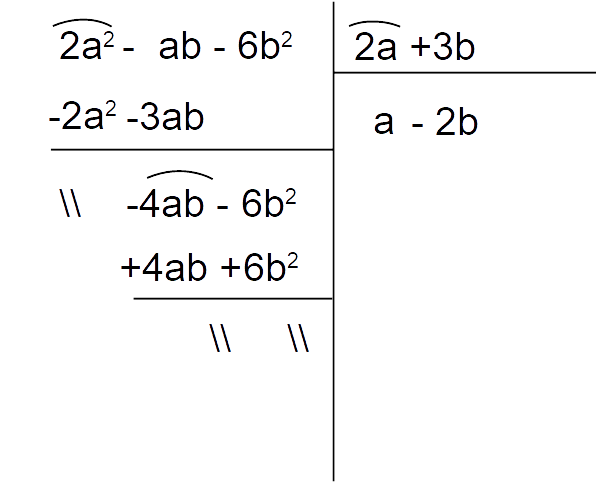
Come possiamo vedere in entrambi i casi otteniamo resto zero. Di conseguenza valgono le scomposizioni:

\begin{align*} & 3a^2-7ab+4b^2=(3a-4b)(a-b) \\ \\ & 2a^2-ab-6b^2=(2a+3b)(a-2b)\end{align*}

Infatti il prodotto del quoziente esatto per il divisore restituisce il dividendo.

Avremmo anche potuto procedere in una maniera diversa, scomponendo direttamente entrambi i polinomi con la regola del trinomio caratteristico (nel caso del trinomio caratteristico con più lettere).

Ad esempio, consideriamo il primo polinomio:

3a^2-7ab+4b^2

Consideriamo la lettera {a} come variabile e la lettera {b} come parametro. Abbiamo in questo modo un trinomio di secondo grado con coefficiente del termine di grado massimo pari a {3}, coefficiente del termine di primo grado pari a {-7b} e termine noto {4b^2}:

3 \cdot a^2 -7b \cdot a +4b^2

Secondo la regola del trinomio caratteristico con coefficiente del termine di secondo grado diverso da {1}, dobbiamo ricercare due monomi aventi per somma {-7b} (il coefficiente del termine di primo grado rispetto alla variabile scelta {a}) e aventi prodotto uguale al prodotto fra il termine noto e il coefficiente del termine in {a^2} (quindi { 4 b^2 \cdot 3 = 12 b^2}). I due monomi sono {-4b} e {-3b}, per cui abbiamo:

\begin{align*} & 3 \cdot a^2 -7b \cdot a +4b^2=3a^2+(-4b-3b) a+4b^2= \\ \\ & =3a^2-4b \cdot a-3b \cdot a+4b^2=3a^2-4ab-3ab+4b^2 =\\ \\ & =3a^2-3ab+4b^2-4ab=3a(a-b)-4b(-b+a)=\\ \\ & =(a-b)(3a-4b)\end{align*}

Procedendo allo stesso modo per il trinomio {2a^2-ab-6b^2} otteniamo:

\small \begin{align*} & 2a^2-ab-6b^2=2 \cdot a^2-b \cdot a -6b^2 = 2a^2+(-4b+3b)a-6b^2= \\ \\ & =2a^2-4ab+3ab-6b^2=2a(a-2b)+3b(a-2b)=(a-2b)(2a+3b)\end{align*}

Ritroviamo così le stesse scomposizioni ottenute con le divisioni.

Osserviamo che volendo evitare la scomposizione con il trinomio caratteristico con più lettere, un modo più elegante per scomporre i polinomi è quello di individuare una radice per ciascun monomio e quindi eseguire la divisione con la regola di Ruffini. Anche in questo caso è prima di tutto necessario scegliere una lettera come variabile, e quindi ricercare un monomio contenente l’altra lettera che annulla il polinomio. Ad esempio, per il primo polinomio, scegliendo come variabile la lettera {a}:

3a^2-7ab+4b^2=3 \cdot a^2 - 7b \cdot a + 4b^2

Individuiamo come radice il monomio {b}. Infatti:

3 \cdot a^2 - 7b \cdot a + 4b^2 \quad \text{con} \quad a=b \quad \Rightarrow \quad 3b^2-7b^2+4b^2=0

Così sappiamo per il teorema di Ruffini che il polinomio è divisibile per {a-b}. Con la regola di Ruffini otteniamo:

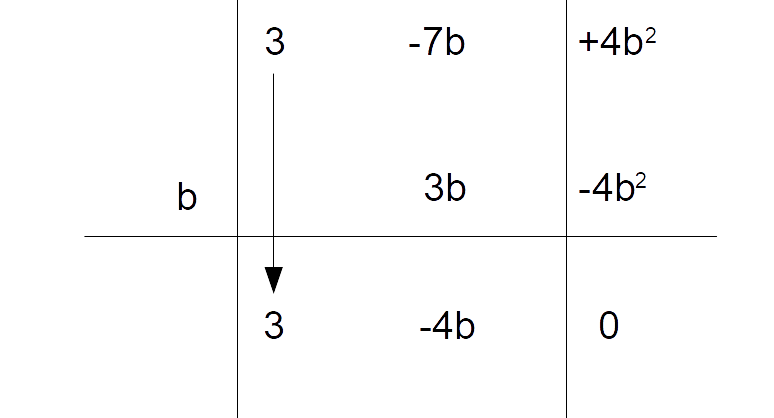
Così otteniamo il quoziente {3a-4b} e quindi possiamo scrivere la scomposizione:

3a^2-7ab+4b^2=(3a-4b)(a-b)

e ritroviamo la scomposizione ottenuta con gli altri metodi. Allo stesso modo è possibile procedere con l’altro polinomio.

Qui abbiamo illustrato diversi metodi per scomporre trinomi caratteristici con più lettere: a voi scegliere il metodo più congeniale.

Ora riprendiamo l’espressione di partenza. Con le scomposizioni appena scritte abbiamo:

\begin{align*} & \dfrac{3a^2-7ab+4b^2}{2a^2-ab-6b^2} \cdot\dfrac{(a^3-8b^3)(2a+3b)}{(a^4-b^4)(3a-4b)}= \\ \\ & = \dfrac{\cancel{(3a-4b)}(a-b)}{(a-2b)\cancel{(2a+3b)}} \cdot\dfrac{(a^3-8b^3)\cancel{(2a+3b)}}{(a^4-b^4)\cancel{(3a-4b)}}= \\ \\ & = \dfrac{(a-b)(a^3-8b^3)}{(a-2b)(a^4-b^4)}=\end{align*}

Ci ritroviamo a questo punto con due fattori che possono essere scomposti rispettivamente con la differenza tra due cubi e la differenza tra quadrati. Proseguendo i passaggi:

=\dfrac{\cancel{(a-b)}\cancel{(a-2b)}(a^2+2ab+4b^2)}{\cancel{(a-2b)}(a+b)\cancel{(a-b)}(a^2+b^2)}=\dfrac{a^2+2ab+4b^2}{(a+b)(a^2+b^2)}

E siamo arrivati al risultato finale.

Per meglio comprendere le scomposizioni in fattori negli ultimi passaggi, osserviamo che si ha:

\small a^3-8b^3=(a)^3-(2b)^3=(a-2b)[\underbrace{a^2+2ab+(2b)^2}_{\text{falso quadrato di }a+2b}]=(a-2b)(a^2+2ab+4b^2)

e inoltre, sfruttando per due volte la regola di scomposizione della differenza tra quadrati:

a^4-b^4=(a^2)^2-(b^2)^2=(a^2-b^2)(a^2+b^2)=(a+b)(a-b)(a^2+b^2)

Esercizio 5

Proseguiamo gli esercizi sulle espressioni con le frazioni algebriche con la seguente:

\dfrac{6a^3+a^2-21a-10}{a^5-3a^4+3a^2+1}:\dfrac{2a^2-3a-2}{a^4-4a^3+4a^2-a+1}

Passiamo anzitutto dalla divisione alla moltiplicazione (ricordiamo di scambiare di posto tra loro il numeratore e il denominatore della frazione a divisore):

\begin{align*} &\dfrac{6a^3+a^2-21a-10}{a^5-3a^4+3a^2+1}:\dfrac{2a^2-3a-2}{a^4-4a^3+4a^2-a+1}=\\ \\ & =\dfrac{6a^3+a^2-21a-10}{a^5-3a^4+3a^2+1}\cdot\dfrac{a^4-4a^3+4a^2-a+1}{2a^2-3a-2}=\end{align*}

Osserviamo che ai numeratori e ai denominatori delle frazioni ci ritroviamo con tre polinomi da scomporre con la regola di Ruffini e un polinomio da scomporre con la regola del trinomio caratteristico.

Cerchiamo di trovare una strada un po’ più breve. Scomponiamo per ora soltanto il trinomio caratteristico al denominatore della seconda frazione:

2a^2-3a-2=2a^2-4a+a-2=2a(a-2)+a-2=(a-2)(2a+1)

Così abbiamo per l’espressione di partenza, proseguendo i passaggi:

=\dfrac{6a^3+a^2-21a-10}{a^5-3a^4+3a^2+1}\cdot\dfrac{a^4-4a^3+4a^2-a+1}{(a-2)(2a+1)}=

A questo punto vediamo se il polinomio {6a^3+a^2-21a-10} è divisibile per uno dei due binomi al denominatore della seconda frazione. Proviamo con il binomio {a-2}, che è già nella forma {a-c} (vedi teorema di Ruffini). L’eventuale radice del polinomio {6a^3+a^2-21a-10} è {c}, ovvero {2}. Abbiamo:

6a^3+a^2-21a-10 \quad \text{con} \quad a = 2 \quad \Rightarrow \quad 6\cdot2^3 + 2^2-21 \cdot 2 -10 = 0

Quindi effettivamente {a-2} è un divisore del polinomio {6a^3+a^2-21a-10}. Eseguiamo allora la divisione {(6a^3+a^2-21a-10):(a-2)} con la regola di Ruffini:

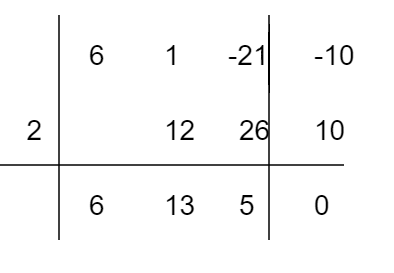
Effettivamente otteniamo resto zero e possiamo scrivere:

6a^3+a^2-21a-10 =(a-2)(6a^2+13a+5)

Cosi riprendendo i passaggi relativi all’espressione con frazioni algebriche:

\begin{align*} & =\dfrac{\cancel{(a-2)}(6a^2+13a+5)}{a^5-3a^4+3a^2+1}\cdot\dfrac{a^4-4a^3+4a^2-a+1}{\cancel{(a-2)}(2a+1)}= \\ \\ & = \dfrac{6a^2+13a+5}{a^5-3a^4+3a^2+1}\cdot\dfrac{a^4-4a^3+4a^2-a+1}{2a+1}=\end{align*}

Ora piuttosto che scomporre il trinomio {6a^2+13a+5} con la regola del trinomio caratteristico, vediamo se troviamo una sua radice. In particolare, vogliamo vedere se delle volte tale trinomio è divisibile per {2a+1}, in modo da eseguire una semplificazione incrociata. Riduciamo allora il binomio {2a+1} alla forma {a-c}, ottenendo {a+\dfrac{1}{2}}. Attenzione: quest’ultimo binomio è la metà di {2a+1}! Di conseguenza, una volta trovato l’eventuale quoziente esatto dovremo dividerlo per {2}.

Per testare se {a+\dfrac{1}{2}} è divisore di {6a^2+13a+5}, testiamo se il valore {-\dfrac{1}{2}} annulla il polinomio:

6a^2+13a+5 \quad \text{con} \quad a=-\dfrac{1}{2} \quad \Rightarrow \quad 6 \cdot \dfrac{1}{4}-13 \cdot \dfrac{1}{2}+5=0

Ci siamo. Eseguiamo la divisione {(6a^2+13a+5):\left(a-\dfrac{1}{2}\right)} con la regola di Ruffini:

Abbiamo ottenuto il quoziente {6a+10}, che diviso per due è uguale a {3a+5}. Per cui vale la scomposizione {6a^2+13a+5=(3a+5)(2a+1)}. Di conseguenza proseguendo i passaggi relativi all’espressione:

\begin{align*} & = \dfrac{(3a+5)\cancel{(2a+1)}}{a^5-3a^4+3a^2+1}\cdot\dfrac{a^4-4a^3+4a^2-a+1}{\cancel{2a+1}}= \\ \\ & = \dfrac{(3a+5)(a^4-4a^3+4a^2-a+1)}{a^5-3a^4+3a^2+1}  \end{align*}

Ormai il meccanismo è chiaro: vediamo se {3a+5} è un divisore di {a^5-3a^4+3a^2+1}. Riduciamo il binomio alla forma {a-c}, ottenendo {a+\dfrac{5}{3}} (ricordiamoci poi di dividere l’eventuale quoziente esatto che otterremo per tre). Vediamo se {c=-\dfrac{5}{3}} è una radice per il polinomio {a^5-3a^4+3a^2+1}:

a^5-3a^4+3a^2+1 \quad \text{con} \quad a=-\dfrac{5}{3} \quad \Rightarrow \quad  \text{diverso da zero}

Questa volta non possiamo adottare questa scorciatoia. A questo punto bisogna procedere scomponendo con la regola di Ruffini entrambi i polinomi di quarto e quinto grado. Oppure, un’alternativa è vedere se delle volte la divisione tra il polinomio di quinto grado e quello di quarto grado restituisce resto zero. In caso affermativo, possiamo sostituire il rapporto tra il polinomio di quarto grado e quello di quinto grado con il reciproco del quoziente di tale divisione. Proviamo ad eseguire allora la divisione:

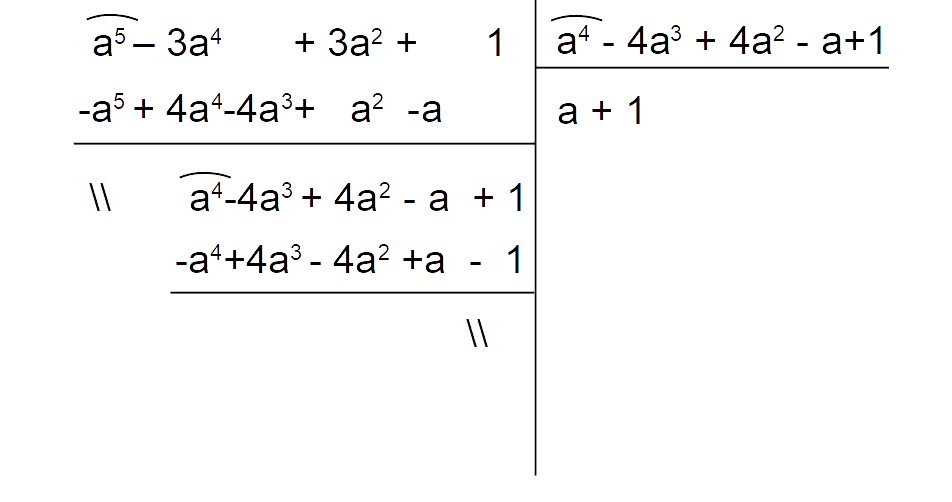
Effettivamente otteniamo resto zero. Per cui per l’espressione abbiamo:

\begin{align*} & \dfrac{(3a+5)(a^4-4a^3+4a^2-a+1)}{a^5-3a^4+3a^2+1}  =(3a+5) \cdot \dfrac{}{}\dfrac{a^4-4a^3+4a^2-a+1}{a^5-3a^4+3a^2+1} =\\ \\ & =(3a+5) \cdot \dfrac{1}{a+1} =\dfrac{3a+5}{a+1}\end{align*}

Abbiamo così semplificato l’espressione di partenza. Osserviamo che in generale se la divisione non avesse restituito un quoziente esatto (cioè non avessimo ottenuto resto zero), avremmo dovuto procedere per forza scomponendo entrambi i polinomi con la regola di Ruffini e quindi semplificando gli eventuali fattori in comune.

Esercizio 6

\left( 2x-y+\dfrac{y^2}{2x+y } \cdot \dfrac{}{} \dfrac{x-2y}{x^2y^2}-\dfrac{4x^2-y^2}{2x+y}\right):\dfrac{x-2y}{2x+y}

In modo simile alle espressioni precedenti, riscriviamo la divisione come una moltiplicazione ed eseguiamo i calcoli all’interno delle parentesi tonde:

\begin{align*} &\left( 2x-y+\dfrac{\cancel{y^2}}{2x+y } \cdot \dfrac{}{} \dfrac{x-2y}{x^2\cancel{y^2}}-\dfrac{4x^2-y^2}{2x+y}\right):\dfrac{x-2y}{2x+y} = \\ \\ & =\left( 2x-y+\dfrac{x-2y}{x^2(2x+y)}-\dfrac{\cancel{(2x+y)}(2x-y)}{\cancel{2x+y}}\right) \cdot \dfrac{{2x+y}}{x-2y}= \\ \\ & = \left( 2x-y+\dfrac{x-2y}{x^2(2x+y)}-(2x-y)\right) \cdot \dfrac{{2x+y}}{x-2y}= \end{align*}

Osserviamo a questo punto che le due quantità {2x-y} all’interno delle parentesi tonde si cancellano tra di loro. Non c’è bisogno di mettere tutti i termini a denominatore comune per eseguire tale semplificazione. Proseguendo i passaggi:

\begin{align*} &= \left( \cancel{2x-y}+\dfrac{x-2y}{x^2(2x+y)}-\cancel{(2x-y)}\right) \cdot \dfrac{{{2x+y}}}{x-2y}=  \\ \\ & =\dfrac{\cancel{x-2y}}{x^2\cancel{(2x+y)}} \cdot \dfrac{\cancel{2x+y}}{\cancel{x-2y}} = \dfrac{1}{x^2}\end{align*}

Esercizio 7

Proseguiamo ancora gli esercizi sulle espressioni con frazioni algebriche con la seguente:

\left[ \dfrac{a}{4-6a}+\dfrac{3a}{9a^2-12a+4} \cdot \left( \dfrac{3a+1}{3a}-\dfrac{3}{2}\right)\right] \cdot \dfrac{4-9a^2}{a^2+2a+1}

Scomponiamo i numeratori e i denominatori delle frazioni algebriche ove possibile, inoltre eseguiamo i calcoli all’interno delle parentesi tonde.

\begin{align*} &\left[ \dfrac{a}{4-6a}+\dfrac{3a}{9a^2-12a+4} \cdot \left( \dfrac{3a+1}{3a}-\dfrac{3}{2}\right)\right] \cdot \dfrac{4-9a^2}{a^2+2a+1} = \\ \\ & = \left[ \dfrac{a}{2(2-3a)}+\dfrac{3a}{(3a-2)^2}\cdot\dfrac{6a+2-9a}{6a}\right] \cdot \dfrac{(2+3a)(2-3a)}{(a+1)^2}= \\ \\ & =\left[ \dfrac{a}{2(2-3a)}+\dfrac{3a}{(3a-2)^2}\cdot\dfrac{-3a+2}{6a}\right] \cdot \dfrac{(2+3a)(2-3a)}{(a+1)^2} = \end{align*}

Attenzione: non è possibile semplificare a croce il fattore al denominatore della prima frazione algebrica! Infatti, la prima frazione algebrica è sommata algebricamente al prodotto tra le altre due frazioni. Per cui non possiamo semplificare il fattore a denominatore di tale frazione con il numeratore della terza frazione algebrica. Le semplificazioni incrociate si possono eseguire solo in corrispondenza di moltiplicazioni.

Ora aggiustiamo i segni in una frazione algebrica all’interno delle parentesi quadre, in modo da poter eseguire una semplificazione incrociata (ci riferiamo al prodotto tra due frazioni algebriche). In generale è possibile cambiare il segno di tutti i termini a numeratore e denominatore di una frazione, ottenendo una frazione equivalente a quella data.

\begin{align*} &\left[ \dfrac{a}{2(2-3a)}+\dfrac{\cancel{3a}}{({3a-2}^{})^{\cancel{2}}}\cdot\dfrac{\overbrace{\cancel{{3a-2}}}^{-(-3a+2)}}{\underbrace{\cancel{-6}^{\scriptsize \displaystyle-2}\cancel{a}}_{-(6a)}}\right] \cdot \dfrac{(2+3a)(2-3a)}{(a+1)^2} = \\ \\ & =\left[\dfrac{a}{2(2-3a)} +\dfrac{1}{-2(3a-2)}\right] \cdot \dfrac{(2+3a)(2-3a)}{(a+1)^2}= \end{align*}

A questo punto lavoriamo sui segni relativamente alla seconda frazione algebrica dentro le parentesi quadre (moltiplichiamo entrambi i fattori del denominatore per {-1}). In questo modo le due frazioni all’interno delle parentesi quadre hanno lo stesso denominatore:

\begin{align*} & =\left[ \dfrac{a}{2(2-3a)}+\dfrac{1}{2(-3a+2)}\right] \cdot \dfrac{(2+3a)(2-3a)}{(a+1)^2}=  \\ \\ & =\dfrac{\cancel{a+1}}{2\cancel{(2-3a})} \cdot \dfrac{{(2+3a)}\cancel{(2-3a)}}{(a+1)^{\cancel{2}}} =\dfrac{2+3a}{2(a+1)} \end{align*}

E siamo arrivati. Ovviamente non è possibile semplificare i {2} tra loro. Il {2} al numeratore è infatti un addendo e tale semplificazione andrebbe contro la proprietà invariantiva della divisione.

Esercizio 8

Concludiamo questa serie di esercizi sulle espressioni con le frazioni algebriche con la seguente espressione:

\small\left[ \dfrac{x^2-(1+y)^2}{x-y-1}+\dfrac{x^2-(1+y)^2}{x+y+1}-\dfrac{2x^2-2xy}{x+y}+\dfrac{x^4+x^2y^2+y^4}{x^2+xy+y^2}\right] \cdot \dfrac{x^3+y^3}{x^3+4xy+y^3}

Eseguiamo tutte le scomposizioni in fattori ove possibile. Osserviamo che per la quantità {x^2-(1+y)^2} è una differenza tra quadrati e si ha:

x^2-(1+y)^2=[x+(1+y)][x-(1+y)]=(x+1+y)(x-1-y)

Così abbiamo:

\small \begin{align*} &\left[ \dfrac{x^2-(1+y)^2}{x-y-1}+\dfrac{x^2-(1+y)^2}{x+y+1}-\dfrac{2x^2-2xy}{x+y}+\dfrac{x^4+x^2y^2+y^4}{x^2+xy+y^2}\right] \cdot \dfrac{x^3+y^3}{x^3+4xy+y^3}= \\ \\ & = \left[ \dfrac{(x+1+y)\cancel{(x-1-y)}}{\cancel{x-y-1}}+\dfrac{\cancel{(x+1+y)}(x-1-y)}{\cancel{x+y+1}}-\dfrac{2x(x-y)}{x+y}+\dfrac{x^4+x^2y^2+y^4}{x^2+xy+y^2}\right] \cdot \\ \\ & \cdot \dfrac{(x+y)(x^2-xy+y^2)}{x^3+4xy+y^3}=\\ \\ & =\left[ x+\cancel{1}+\cancel{y}+x-\cancel{1}-\cancel{y}-\dfrac{2x(x-y)}{x+y}+\dfrac{x^4+x^2y^2+y^4}{x^2+xy+y^2}\right] \cdot \dfrac{(x+y)(x^2-xy+y^2)}{x^3+4xy+y^3} = \\ \\ & =\left[ 2x-\dfrac{2x(x-y)}{x+y}+\dfrac{x^4+x^2y^2+y^4}{x^2+xy+y^2}\right] \cdot \dfrac{(x+y)(x^2-xy+y^2)}{x^3+4xy+y^3}=  \end{align*}

Per scomporre il polinomio {x^4+x^2y^2+y^4} (numeratore della terza frazione algebrica all’interno delle parentesi quadre) osserviamo che si ha:

x^4+x^2y^2+y^4=(x^2+y^2)^2-x^2y^2=(x^2+y^2+xy)(x^2+y^2-xy)

Infatti {x^4+x^2y^2+y^4} è il falso quadrato del binomio {x^2+y^2}, e il quadrato di un binomio differisce dal falso quadrato di quello stesso binomio per il prodotto tra i suoi termini.

Così proseguendo i passaggi dell’espressione:

\small \begin{align*} & =\left[ 2x-\dfrac{2x(x-y)}{x+y}+\dfrac{\cancel{(x^2+y^2+xy)}(x^2+y^2-xy)}{\cancel{x^2+xy+y^2}}\right] \cdot \dfrac{(x+y)(x^2-xy+y^2)}{x^3+4xy+y^3} = \\ \\ & = \left[ \dfrac{{2x(x+y)}-{2x(x-y)}+(x+y)(x^2+y^2-xy)}{x+y}\right] \cdot \dfrac{(x+y)(x^2-xy+y^2)}{x^3+4xy+y^3} = \\ \\ & =\left[ \dfrac{{2x(x+y-x+y)}+(x+y)(x^2+y^2-xy)}{x+y}\right] \cdot \dfrac{(x+y)(x^2-xy+y^2)}{x^3+4xy+y^3} = \\ \\ & =\left[ \dfrac{4xy+(x+y)(x^2+y^2-xy)}{x+y}\right] \cdot \dfrac{(x+y)(x^2-xy+y^2)}{x^3+4xy+y^3}=\end{align*}

A questo punto dobbiamo osservare che per il prodotto notevole della somma di cubi abbiamo:

(x+y)(x^2+y^2-xy)=x^3+y^3

Così proseguendo i passaggi relativamente all’espressione:

\begin{align*} &=  \dfrac{\cancel{4xy+x^3+y^3}}{\cancel{x+y}} \cdot \dfrac{\cancel{(x+y)}(x^2-xy+y^2)}{\cancel{x^3+4xy+y^3}}=x^2-xy+y^2\end{align*}

ed abbiamo concluso.

Per quanto riguarda questa lezione relativa agli esercizi sulle espressioni con le frazioni algebriche è tutto. Ricordiamo la lezione sulle operazioni con le frazioni algebriche per rivedere le regole se necessario. Sono infine disponibili le schede di esercizi per chi vuole allenarsi ulteriormente. Buon proseguimento con SìMatematica!